|
|
|
|
Билеты: Алгебра и Начало анализа
Билеты: Алгебра и Начало анализа
Алгебра и начала анализа. |  1. Линейная функция y = ax + b, её свойства и график. 1. Линейная функция y = ax + b, её свойства и график.
| Ответ |  2. Квадратичная функция y = ax2 + bx + c, её свойства и график. 2. Квадратичная функция y = ax2 + bx + c, её свойства и график.
| Ответ |  3. Функция y = k/x, её свойства и график, график дробно-линейной функции (на конкретном приме-ре). 3. Функция y = k/x, её свойства и график, график дробно-линейной функции (на конкретном приме-ре).
| Ответ |  4. Показательная функция y = ax, её свойства и график. 4. Показательная функция y = ax, её свойства и график.
| Ответ |  5. Логарифмическая функция y = logax, её свойства и график. 5. Логарифмическая функция y = logax, её свойства и график.
| Ответ |  6. Функция y = sin(x), её свойства и график. 6. Функция y = sin(x), её свойства и график.
| Ответ |  7. Функция y = cos(x), её свойства и график. 7. Функция y = cos(x), её свойства и график.
| Ответ |  8. Функция y = tg(x), её свойства и график. 8. Функция y = tg(x), её свойства и график.
| Ответ |  9. Функция y = ctg(x), её свойства и график. 9. Функция y = ctg(x), её свойства и график.
| Ответ |  10. Арифметическая прогрессия, сумма первых n членов арифметической прогрессии. 10. Арифметическая прогрессия, сумма первых n членов арифметической прогрессии.
| Ответ |  11. Геометрическая прогрессия, сумма первых n членов геометрической прогрессии. Сумма бесконечно убывающей геометрической прогрессии. 11. Геометрическая прогрессия, сумма первых n членов геометрической прогрессии. Сумма бесконечно убывающей геометрической прогрессии.
| Ответ |  12. Решение уравнения sin(x) = a, неравенств sin(x) > a, sin(x) < a. 12. Решение уравнения sin(x) = a, неравенств sin(x) > a, sin(x) < a.
| Ответ |  13. Решение уравнения cos(x) = a, неравенств cos(x) > a, cos(x) < a. 13. Решение уравнения cos(x) = a, неравенств cos(x) > a, cos(x) < a.
| Ответ |  14. Решение уравнения tg(x) = a, неравенств tg(x) > a, tg(x) < a. 14. Решение уравнения tg(x) = a, неравенств tg(x) > a, tg(x) < a.
| Ответ |  15. Формулы приведения (с выводом). 15. Формулы приведения (с выводом).
| Ответ |  16. Формулы синуса и косинуса суммы и разности двух аргументов (с доказательством). 16. Формулы синуса и косинуса суммы и разности двух аргументов (с доказательством).
| Ответ |  17. Тригонометрические функции двойного аргумента. 17. Тригонометрические функции двойного аргумента.
| Ответ |  18. Тригонометрические функции половинного аргумента. 18. Тригонометрические функции половинного аргумента.
| Ответ |  19. Формулы суммы и разности синусов, косинусов (с доказательством). 19. Формулы суммы и разности синусов, косинусов (с доказательством).
| Ответ |  20. Вывод формулы корней квадратного уравнения, теорема Виета. 20. Вывод формулы корней квадратного уравнения, теорема Виета.
| Ответ |  21. Логарифм произведения, степени, частного. 21. Логарифм произведения, степени, частного.
| Ответ |  22. Понятие производной, ее геометрический смысл и физический смысл. 22. Понятие производной, ее геометрический смысл и физический смысл.
| Ответ |  23. Правила вычисления производной. 23. Правила вычисления производной.
| Ответ |
- Функция заданная формулой y = kx + b, где k и b - некоторые числа,
называется линейной.
- Областью определения линейной
функции служит множество R всех действительных чисел, т.к.
выражение kx + b имеет смысл при любых значениях х.
- График
линейной функции y = kx + b есть прямая. Для построения графика, очевидно,
достаточно двух точек, если k
 0.
0. - Коэффициент k характеризует угол, который образует прямая y
= kx с положительным направлением оси Ох, поэтому k называется угловым
коэффициентом. Если k > 0, то этот угол острый; если k < 0 - тупой;
если k = 0, то прямая совпадает с осью Ох.
- График функции
y = kx + b может быть постпоен с помощью параллельного переноса графика
функции y = kx.
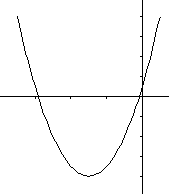
 Ответ №2. Опр. Квадратичной функцией называется функция, которую можно
задать формулой вида y = ax2 + bx + c, где х - независимая
переменная, а, b и с - некоторые числа, причем а
Ответ №2. Опр. Квадратичной функцией называется функция, которую можно
задать формулой вида y = ax2 + bx + c, где х - независимая
переменная, а, b и с - некоторые числа, причем а  0.
Графиком квадратичной функции является парабола.
Свойства функции y = ax2(частный случай) при а > 0.
1. Если х = 0, то y = 0. График функции проходит через начало координат.
2. Если х
0.
Графиком квадратичной функции является парабола.
Свойства функции y = ax2(частный случай) при а > 0.
1. Если х = 0, то y = 0. График функции проходит через начало координат.
2. Если х  0, то y > 0. График функции расположен в верхней полуплоскости.
3. График функции симметричен относительно оси Oy.
4. Функция убывает в промежутке (- 0, то y > 0. График функции расположен в верхней полуплоскости.
3. График функции симметричен относительно оси Oy.
4. Функция убывает в промежутке (-  ; 0] и возрастает в промежутке [0; + ; 0] и возрастает в промежутке [0; +  ).
5. Наименьшее значение функция принимает при х = 0. Область значений функции [0;
+ ).
5. Наименьшее значение функция принимает при х = 0. Область значений функции [0;
+  ).
Свойства функции y = ax2 при а < 0.
1. Если х = 0, то y = 0. График функции проходит через начало координат.
2. Если х ).
Свойства функции y = ax2 при а < 0.
1. Если х = 0, то y = 0. График функции проходит через начало координат.
2. Если х  0, то y < 0. График функции расположен в нижней полуплоскости.
3. График функции симметричен относительно оси Oy.
4. Функция убывает в промежутке [0; + 0, то y < 0. График функции расположен в нижней полуплоскости.
3. График функции симметричен относительно оси Oy.
4. Функция убывает в промежутке [0; +  ) и возрастает в промежутке (- ) и возрастает в промежутке (-  ; 0].
5. Наименьшее значение функция принимает при х = 0. Область значений функции (- ; 0].
5. Наименьшее значение функция принимает при х = 0. Область значений функции (-  ; 0].
И, так, график функции y = ax2 + bx + c есть парабола, вершиной
которой является точка (m; n), где m =
; 0].
И, так, график функции y = ax2 + bx + c есть парабола, вершиной
которой является точка (m; n), где m = 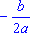 , n=
, n= 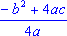 . Осью симметрии параболы
служит прямая х = m, параллельная оси y. При а > 0 ветви параболы направлены
вверх, при a < 0 - вниз. . Осью симметрии параболы
служит прямая х = m, параллельная оси y. При а > 0 ветви параболы направлены
вверх, при a < 0 - вниз.
 Ответ 3
Если переменная у обратно пропорциональна переменной х, то эта зависимость
выражается формулой
Ответ 3
Если переменная у обратно пропорциональна переменной х, то эта зависимость
выражается формулой 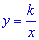 , где , где  - коэффициент обратной пропорциональности.
- коэффициент обратной пропорциональности.
- Область определения функции
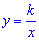 - есть множество всех чисел, отличных от нуля, т. е.
- есть множество всех чисел, отличных от нуля, т. е. 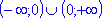 .
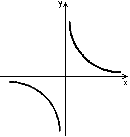
. - Графиком обратной пропорциональности у=k/x является
кривая, состоящая из двух ветвей, симметричных относительно начала
координат. Такая кривая называется гиперболой. Если k>0, то ветви
гиперболы расположены в I и III координатных четвертях; если же k<.0,
то во II и IV координатных четвертях.
- Заметим, что
гипербола не имеет общих точек с осями координат, а лишь сколь угодно
близко к ним приближается.
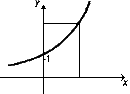
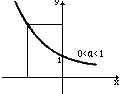
 № 4. Опр. Функция, заданная формулой y = ax, где а - некоторое
положительное число, не равное еденице, называется показательной.
1. Функция y = ax при а>1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то ax > 1;
е) если х < 0, то 0< ax <1;
2. Функция y = ax при 0< а <1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0< ax <1;
е) если х < 0, то ax > 1.
№ 4. Опр. Функция, заданная формулой y = ax, где а - некоторое
положительное число, не равное еденице, называется показательной.
1. Функция y = ax при а>1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то ax > 1;
е) если х < 0, то 0< ax <1;
2. Функция y = ax при 0< а <1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0< ax <1;
е) если х < 0, то ax > 1.
  №5.Опр. Функцию, заданную формулой y = loga x называют
логарифмической функцией с основанием а.
Свойства функции y = loga x при a>1:
а) D(f) = R+;
б) E(f) = R;
в) функция возрастает;
г) если x = 1, то loga x = 0;
д) если 0<x<1, то loga x < 0;
е) если x > 1, то loga x > 0.
Свойства функции y = loga x при 0<a<1:
а) D(f) = R+;
б) E(f) = R;
в) функция убывает;
г) если x = 1, то loga x = 0;
д) если 0 < x < 1, то loga x > 0;
е) если x > 1, то loga x < 0.
№5.Опр. Функцию, заданную формулой y = loga x называют
логарифмической функцией с основанием а.
Свойства функции y = loga x при a>1:
а) D(f) = R+;
б) E(f) = R;
в) функция возрастает;
г) если x = 1, то loga x = 0;
д) если 0<x<1, то loga x < 0;
е) если x > 1, то loga x > 0.
Свойства функции y = loga x при 0<a<1:
а) D(f) = R+;
б) E(f) = R;
в) функция убывает;
г) если x = 1, то loga x = 0;
д) если 0 < x < 1, то loga x > 0;
е) если x > 1, то loga x < 0.
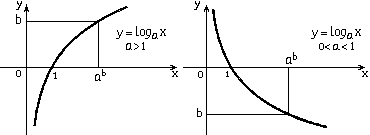 №6. Опр. Отношение катета прямоугольного треугольника, противолежащего
острому углу, к гипотенузе называется синусом этого угла (обозначается sin
№6. Опр. Отношение катета прямоугольного треугольника, противолежащего
острому углу, к гипотенузе называется синусом этого угла (обозначается sin  ).
).
- область определения - множество всех действительных чисел;
-
множество значений - [-1; 1];
- функция нечетная: sin(-x) =
-sin(x) для всех
 ; ; -
функция периодическая с наименьшим положительным периодом
 ;
; - sin(x) = 0 при x =
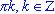 ;
; - sin(x) > 0 для всех
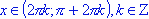 ;
; - sin(x) < 0 для всех
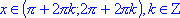 ;
; - функция возрастает на
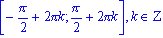 ;
; - функция убывает на
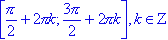 .
.
 № 7.Опр. Отношение катета прямоугольного треугольника, прилежащего к
острому углу, к гипотенузе называется косинусом этого угла (обозначается
cos
№ 7.Опр. Отношение катета прямоугольного треугольника, прилежащего к
острому углу, к гипотенузе называется косинусом этого угла (обозначается
cos  ) )
- область определения - множество всех действительных чисел;
-
множество значений - [-1; 1];
- функция четная: cos(-x) =
cos(x) для всех
 ; ; -
функция периодическая с наименьшим положительным периодом
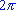 ;
; - cos(x) = 0 при
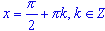 ;
; - cos(x) > 0 для всех
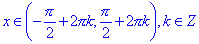 ;
; - cos(x) > 0 для всех
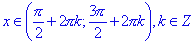 ;
; - функция возрастает на
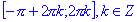 ;
; - функция убывает на
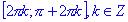
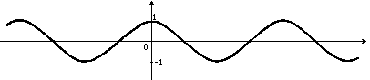 №8.Опр. Отношение катета, противолежащего острому углу прямоугольного
треугольника, к катету, прилежащему к этому углу, называется тангенсом
(обозначается tg
№8.Опр. Отношение катета, противолежащего острому углу прямоугольного
треугольника, к катету, прилежащему к этому углу, называется тангенсом
(обозначается tg  ). ).
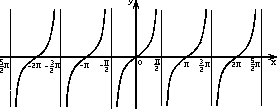
- область определения - множество всех действительных чисел, кроме
чисел вида
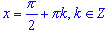 ; ; -
множество значений - вся числовая прямая;
- функция
нечетная: tg(-x) = -tg(x) для всех х из области определения;
-
функция периодическая с наименьшим положительным периодом
 ;
; - tg(x) = 0 при х =
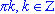 ;
; - tg(x) > 0 для всех
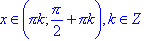 ;
; - tg(x) < 0 для всех
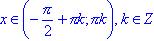 ;
; - функция возрастает на
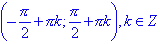 .
.
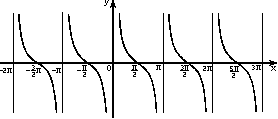
 №9.Опр. Отношение катета, прилежащего острому углу прямоугольного
треугольника, к катету, противолежащему к этому углу, называется котангенсом
(обозначается ctg
№9.Опр. Отношение катета, прилежащего острому углу прямоугольного
треугольника, к катету, противолежащему к этому углу, называется котангенсом
(обозначается ctg  ) )
- область определения - множество всех действительных чисел, кроме
чисел вида
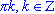 ; ; -
множество значений - вся числовая прямая;
- функция
нечетная: ctg(-x) = -ctg(x) для всех х из области определения;
-
функция периодическая с наименьшим положительным периодом
 ;
; - ctg(x) = 0 при x =
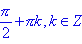 ;
; - ctg(x) > 0 для всех
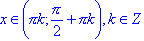 ;
; - ctg(x) < 0 для всех
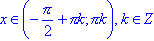 ;
; - функция убывает на
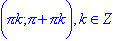 .
.
 Ответ № 10
Ответ № 10
- Числовая последовательность, каждый член которой, начиная со
второго, равен предшествующему члену, сложенному с одним и тем же числом,
называется арифметической прогрессией.
- Из определения
арифметической прогрессии следует, что разность между любым ее членом и
ему предшествующим равна одному и тому же числу, т. е. а2 - а
1 = а3 - а2 = ... = ak - ak-1
= ... . Это число называется разностью арифметической прогрессии и обычно
обозначается буквой d.
- Для того чтобы задать
арифметическую прогрессию (аn), достаточно знать ее первый член
а1 и разность d.
- Если разность
арифметической прогрессии - положительное число, то такая прогрессия
является возрастающей; если отрицательное число, то убывающей. Если
разность арифметической прогрессии равна нулю, то все ее члены равны между
собой и прогрессия является постоянной последовательностью.
-
Характеристическое свойство арифметической прогрессии. Последовательность
(аn) является арифметической прогрессией тогда и только тогда, когда любой
ее член, начиная со второго, является средним арифметическим
предшествующего и последующего членов, т. е.
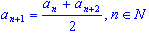 (1)
(1) - Формула n-го члена арифметической прогрессии имеет вид:
an = a1 + d(n-1). (2)
- Формула
суммы n первых членов арифметической прогрессии имеет вид:
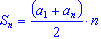 (3)
(3) - Если в формулу (3) подставить вместо аn его
выражение по формуле (2), то получим соотношение
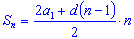 -
Из определения разности арифметической прогрессии следует, что a1
+ an = a2 + an-1 = ..., т. е. сумма
членов, равноудаленных от концов прогрессии, есть величина постоянная.
Ответ № 11
- Числовая последовательность, первый член которой отличен от нуля, а
каждый член, начиная со второго, равен предшествующему члену, умноженному
на одно и то же не равное нулю число, называется геометрической
прогрессией.
- Из определения геометрической прогрессии следует,
что отношение любого ее члена к предшествующему равно одному и тому же
числу, т. е. b2:b1 = b3
:b2 = ... = bn:bn-1
= bn+1:bn = ... . Это число называется
знаменателем геометрической прогрессии и обычно обозначается буквой
q.
- Для того, чтобы задать геометрическую
прогрессию (bn), достаточно знать ее первый член b
1 и знаменатель q.
- Если q
> 0 (
 ), то
прогрессия является монотонной последовательностью. Пусть, например, b
1= -2, q = 3, тогда геометрическая прогрессия -2, -6,
-18, ... есть монотонно убывающая последовательность. Если q = 1,
то все члены прогрессии равны между собой. В этом случае прогрессия
является постоянной последовательностью. ), то
прогрессия является монотонной последовательностью. Пусть, например, b
1= -2, q = 3, тогда геометрическая прогрессия -2, -6,
-18, ... есть монотонно убывающая последовательность. Если q = 1,
то все члены прогрессии равны между собой. В этом случае прогрессия
является постоянной последовательностью. - Характеристическое
свойство геометрической прогрессии. Последовательность (bn
) является геометрической прогрессией тогда и только тогда, когда каждый ее
член, начиная со второго, есть среднее геометрическое соседних с ним
членов, т. е.
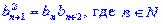 (1) (1) -
Формула n-го члена геометрической прогрессии имеет вид:
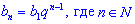 (2)
(2) - Формула суммы п первых членов геометрической
прогрессии имеет вид:
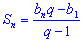 ,
,  (3) (3) - Если в
формулу (3) подставить вместо bn его выражение по формуле (2),
то получится соот-ношение.
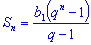 ,
,  (4) (4) - Из
определения знаменателя геометрической прогрессии следует, что b1
bn = b2bn-1 = ., т.е. произведение членов,
равноотстоящих от концов прогрессии, есть величина постоянная.
Сумма бесконечной геометрической прогресси при 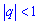
- Пусть (xn) - геометрическая прогрессия со знаменателем
q, где
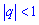 и и 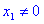 . Суммой бесконечной геометрической прогрессии, знаменатель которой
удовлетворяет условию
. Суммой бесконечной геометрической прогрессии, знаменатель которой
удовлетворяет условию 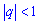 , называется предел суммы n первых ее членов при
, называется предел суммы n первых ее членов при 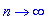 .
. - Обозначим сумму бесконечной геометрической прогрессии через
S. Тогда верна формула
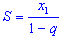 .
.
№ 12
Решение тригонометрических уравнений вида sin(x) = a
- формула для корней уравнения sin(x) = a, где
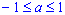 , имеет вид: , имеет вид: 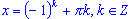 Частные случаи:
Частные случаи: - sin(x) = 0, x =
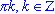 -
sin(x) = 1, x =
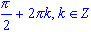 -
sin(x) = -1, x =
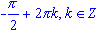 -
формула для корней уравнения sin2(x) = a, где
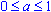 , имеет вид: x=
, имеет вид: x= 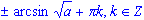
Решение тригонометрических неравенств вида sin(x) > a, sin(x) < a
- Неравенства, содержащие переменную только под знаком
тригонометрической функции, называются тригонометрическими.
- При
решении тригонометрических неравенств используют свойство монотонности
триго-нометрических функций, а также промежутки их знакопостоянства.
-
Для решения простейших тригонометрических неравенств вида sin(x) > a
(sin(x) < а) используют единичную окружность или график функции y =
sin(x).
sin(x) = 0 если х =
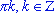 ;
sin(x) = -1, если x = ;
sin(x) = -1, если x = 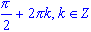 >;
sin(x) > 0, если >;
sin(x) > 0, если 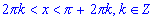 ;
sin(x) < 0, если ;
sin(x) < 0, если 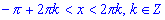 . .
Ответ № 13
Решение тригонометрического уравнения cos(x) = a
- Формула для корней уравнения cos(x) = a, где
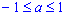 , имеет вид:
, имеет вид: 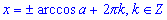 . . -
Частные случаи:
cos(x) = 1, x =
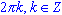 ;
cos(x) = 0, ;
cos(x) = 0, 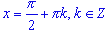 ;
cos(x) = -1, x = ;
cos(x) = -1, x =  -
Формула для корней уравнения cos2(x) = a, где
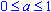 , имеет вид:
, имеет вид: 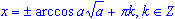 . .
Решение тригонометрических неравенств вида cos(x) > a, cos(x) < a
- Для решения простейших тригонометрических неравенств вида cos(x)
> a, cos(x) < a используют единичную окружность или график функции y
= cos(x);
- Важным моментом является знание, что:
cos(x) = 0, если
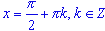 ;
cos(x) = -1, если x = ;
cos(x) = -1, если x =  ;
cos(x) = 1, если x = ;
cos(x) = 1, если x = 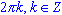 ;
cos(x) > 0, если ;
cos(x) > 0, если 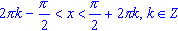 ;
cos(x) > 0, если ;
cos(x) > 0, если 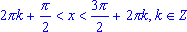 . .
№ 14
Решение тригонометрического уравнения tg(x) = a
- Формула для корней уравнения tg(x) = a имеет вид:
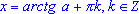 .
. - Частные случаи:
tg(x) = 0, x =
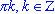 ;
tg(x) = 1, ;
tg(x) = 1, 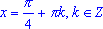 ;
tg(x) = -1, ;
tg(x) = -1, 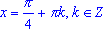 . . -
Формула для корней уравнения tg2(x) = a, где
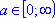 , имеет вид:
, имеет вид: 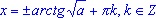
Решение тригонометрических неравенств вида tg(x) > a, tg(x) < a
- Для решения простейших тригонометрических неравенств вида tg(x)
> a, tg(x) < a используют единичную окружность или график функции y
= tg(x).
- Важно знать, что:
tg(x) > 0, если
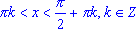 ;
tg(x) < 0, если ;
tg(x) < 0, если 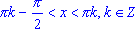 ;
Тангенс не существует, если ;
Тангенс не существует, если 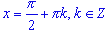 . .
№ 15
- Формулами приведения называются соотношения, с помощью которых
значения тригонометрических функций аргументов
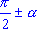 ,
,  , , 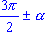 ,
,  , выражаются через
значения sin , выражаются через
значения sin  , cos , cos  , tg
, tg  и ctg и ctg  .
. - Все формулы приведения можно свести в следующую таблицу:
Функция  | Аргумент  | 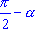
| 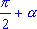
| 
| 
| 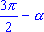
| 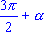
| 
| 
| sin  | cos  | cos  | sin  | -sin  | -cos  | -cos  | -sin  | sin  | cos  | sin  | -sin  | -cos | -cos | -sin  | sin  | cos  | cos  | tg  | ctg  | -ctg  | -tg  | tg  | ctg  | -ctg  | -tg  | tg  | ctg  | tg  | -tg  | -ctg  | ctg  | tg  | -tg  | -ctg  | ctg  |
- Для облегчения запоминания приведенных формул нужно использовать
следующие правила:
a) при переходе от функций углов
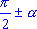 ,
, 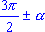 к функциям угла к функциям угла  название функции изменяют: синус на косинус, тангенс на котангенс и
наоборот;
при переходе от функций углов
название функции изменяют: синус на косинус, тангенс на котангенс и
наоборот;
при переходе от функций углов  ,
,  к функциям угла к функциям угла  название функции сохраняют;
б) считая
название функции сохраняют;
б) считая  острым углом
(т. е. острым углом
(т. е. 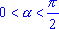 ), перед
функцией угла ), перед
функцией угла  ставят
такой знак, какой имеет приводимая функ-ция углов ставят
такой знак, какой имеет приводимая функ-ция углов 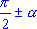 ,
,  , , 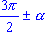 .
.
Все вышеприведенные формулы можно получить, пользуясь следующим правилом:
Любая тригонометрическая функция угла 90°n +  по абсолютной величине равна той же функции угла
по абсолютной величине равна той же функции угла  , если число n - четное, и дополнительной функции, если число n - нечетное. При
этом, если функция угла 90°n +
, если число n - четное, и дополнительной функции, если число n - нечетное. При
этом, если функция угла 90°n +  .
положительна, когда .
положительна, когда  - острый
угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
№ 16 - острый
угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
№ 16
- Формулы косинуса суммы и разности двух аргументов:
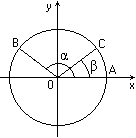 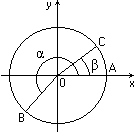 Рис.1 Рис.2
Повернем радиус ОА, равный R, около точки О на угол
Рис.1 Рис.2
Повернем радиус ОА, равный R, около точки О на угол  и на угол
и на угол  (рис.1).
Получим радиусы ОВ и ОС. Найдем скалярное произведение векторов (рис.1).
Получим радиусы ОВ и ОС. Найдем скалярное произведение векторов  и
и  . Пусть координаты
точки В равны х1 и y1, координаты точки С равны х
2 и y2. Эти же координаты имеют соответственно и векторы . Пусть координаты
точки В равны х1 и y1, координаты точки С равны х
2 и y2. Эти же координаты имеют соответственно и векторы  и
и  . По определению
скалярного произведения векторов: . По определению
скалярного произведения векторов:
  = х1х2 + y1y2. (1)
Выразим скалярное произведение = х1х2 + y1y2. (1)
Выразим скалярное произведение   через тригонометрические функции углов
через тригонометрические функции углов  и
и  . Из определения
косинуса и синуса следует, что
х1 = R cos . Из определения
косинуса и синуса следует, что
х1 = R cos  , y1 = R sin , y1 = R sin  , х2 = R cos , х2 = R cos  , y2 = R sin , y2 = R sin  .
Подставив значения х1, х2, y1, y2 в правую часть равенства (1), получим: .
Подставив значения х1, х2, y1, y2 в правую часть равенства (1), получим:
  = R2cos = R2cos cos cos + R2sin + R2sin sin sin = R2(cos = R2(cos cos cos + sin + sin sin sin ).
С другой стороны, по теореме о скалярном произведении векторовимеем: ).
С другой стороны, по теореме о скалярном произведении векторовимеем:
  = = 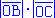 cos cos  BOC = R2cos BOC = R2cos  BOC.
Угол ВОС между векторами BOC.
Угол ВОС между векторами  и и  может быть равен
может быть равен  - -  (рис.1),
(рис.1),  - ( - ( -
-  ) (рис.2) либо
может отличаться от этих значений на целое число оборотов. В любом из этих
случаев cos ) (рис.2) либо
может отличаться от этих значений на целое число оборотов. В любом из этих
случаев cos  BOC = cos ( BOC = cos ( -
-  ). Поэтому ). Поэтому
  = R2 cos ( = R2 cos ( - -  ).
Т.к. ).
Т.к.   равно также R2(cos равно также R2(cos cos cos + sin + sin sin sin ), то
cos( ), то
cos( - -  ) = cos ) = cos cos cos + sin + sin sin sin .
cos( .
cos( + +  ) = cos( ) = cos( - (- - (- )) = cos )) = cos cos(- cos(- ) + sin ) + sin sin(- sin(- ) = cos ) = cos cos cos - sin - sin sin sin .
Значит,
cos( .
Значит,
cos( + +  ) = cos
) = cos cos cos - sin
- sin sin sin .
. - Формулы синуса суммы и разности двух аргументов:
sin(
 + +  ) = cos(
) = cos(  /2 - ( /2 - ( +
+  )) = cos(( )) = cos((  /2 -
/2 -  ) - ) -  ) = cos(
) = cos(  /2 - /2 -  ) cos
) cos + sin( + sin(  /2 -
/2 -  ) sin ) sin = sin
= sin cos cos + cos
+ cos sin sin .
Значит,
sin(
.
Значит,
sin( + +  ) = sin ) = sin cos cos + cos + cos sin sin .
sin( .
sin( - -  ) = sin( ) = sin( + (- + (- )) = sin )) = sin cos(- cos(- ) + cos ) + cos sin(- sin(- ) = sin ) = sin cos cos - cos - cos sin sin .
Значит,
sin( .
Значит,
sin( - -  ) = sin ) = sin cos cos - cos - cos sin sin . .
№ 17
Формулы двойных углов
Формулы сложения позволяют выразить sin 2 , cos 2
, cos 2 , tg 2 , tg 2 , ctg 2
, ctg 2 через тригонометрические
функции угла через тригонометрические
функции угла  .
Положим в формулах
sin( .
Положим в формулах
sin( + +  ) = sin ) = sin cos cos + cos + cos sin sin ,
cos( ,
cos( + +  ) = cos ) = cos cos cos - sin - sin sin sin , ,
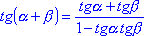 , ,
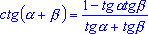 . .
 равным равным  . Получим тождества:
sin 2 . Получим тождества:
sin 2 = 2 sin = 2 sin  cos cos  ;
cos 2 ;
cos 2 = cos2 = cos2  - sin2 - sin2  = 1 - sin2 = 1 - sin2  = 2 cos2 = 2 cos2  - 1; - 1;
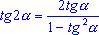 ; ; 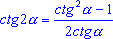 .
№ 18
Формулы половинного аргумента .
№ 18
Формулы половинного аргумента
- Выразив правую часть формулы cos 2
 = cos2
= cos2  - sin
2 - sin
2  через одну
тригонометрическую функцию (синус или косинус), придем к соотношениям
cos 2 через одну
тригонометрическую функцию (синус или косинус), придем к соотношениям
cos 2 = 1 - sin2 = 1 - sin2  , cos 2 , cos 2 = 2 cos2 = 2 cos2  - 1.
Если в данных соотношениях положить - 1.
Если в данных соотношениях положить  = =  /2, то получим:
cos /2, то получим:
cos  = 1 - 2 sin2 = 1 - 2 sin2  /2, cos 2
/2, cos 2 = 2 cos2 = 2 cos2  /2 - 1. (1)
/2 - 1. (1) - Из формул (1) следует, что
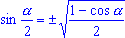 (2), (2), 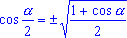 (3).
(3). - Разделив почленно равенство (2) на равенство
(3), получим
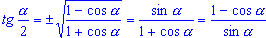 (4). (4). -
В формулах (2), (3) и (4) знак перед радикалом зависит от того, в какой
координатной четверти находится угол
 /2.
/2. - Полезно знать следующую формулу:
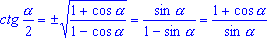 . .
№ 19
Формулы суммы и разности синусов, косинусов
Сумму и разность синусов или косинусов можно представить в виде произведения
тригонометрических функций. Формулы, на которых основано такое
преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin  + sin
+ sin  , положим , положим  = x + y и
= x + y и  = x - y и
воспользуемся формулами синуса суммы и синуса разности. Получим:
sin = x - y и
воспользуемся формулами синуса суммы и синуса разности. Получим:
sin  + sin + sin  = sin (x + y) + sin (x - y) = sinx cosy + cosx siny + sinx cosy - cosx siny =
2sinx cosy.
Решив теперь систему уравнений
= sin (x + y) + sin (x - y) = sinx cosy + cosx siny + sinx cosy - cosx siny =
2sinx cosy.
Решив теперь систему уравнений  =
x + y, =
x + y,  = x - y относительно x
и y, получим х = = x - y относительно x
и y, получим х = 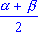 , y = , y = 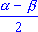 .
Следовательно,
sin
.
Следовательно,
sin  + sin + sin  = 2 sin = 2 sin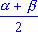 cos cos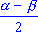 .
Аналогичным образом выводят формулы:
sin .
Аналогичным образом выводят формулы:
sin  -sin -sin  = 2 cos = 2 cos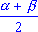 sin sin 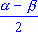 ;
cos ;
cos  + cos + cos  = 2 cos = 2 cos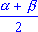 cos cos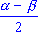 ;
cos ;
cos  + cos + cos  = -2 sin = -2 sin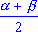 sin sin 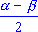 .
№ 20
Чтобы найти решение приведенного квадратного уравнения x2 + p
x + q = 0, где .
№ 20
Чтобы найти решение приведенного квадратного уравнения x2 + p
x + q = 0, где 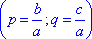 ,
достаточно перенести свободный член в правую часть и к обеем частям равенства
прибавить ,
достаточно перенести свободный член в правую часть и к обеем частям равенства
прибавить 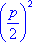 . Тогда левая часть
станет полным квадратом, и мы получаем равносильное уравнение . Тогда левая часть
станет полным квадратом, и мы получаем равносильное уравнение 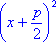 =
= 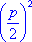 - q .
Оно отличается от простейшего уравнения x2 = m только внешним
видом: - q .
Оно отличается от простейшего уравнения x2 = m только внешним
видом: 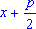 стоит вместо x
и стоит вместо x
и 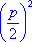 - q - вместо m
. Находим - q - вместо m
. Находим 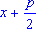 = = 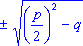 . Отсюба х = -
. Отсюба х = -  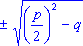 . Эта формула показывает, что всякое квадратное уравнение имеет два корня. Но
эти корни могут быть и мнимыми, если
. Эта формула показывает, что всякое квадратное уравнение имеет два корня. Но
эти корни могут быть и мнимыми, если 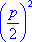 < q . Может также оказаться, что оба корня квадратного уравнения
равны между собой, если
< q . Может также оказаться, что оба корня квадратного уравнения
равны между собой, если 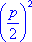 =
q . Возращаемся к обычному виду =
q . Возращаемся к обычному виду 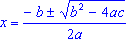 .
1. Сумма корней приведенного квадратного уравнения x2 + px +
q = 0 равна второму коэффициенту, взятому с противоположным знаком, а
произведение корней равно свободному члену, т.е. х1 + х2
= -р, а х1х2 = q .
2. Теорема, обратная теореме Виета. Если р, q, х1, х
2 таковы, что х1 + х2 = -р и х1х
2 = q , то х1 и х2 - корни уравнения x2
+ px + q = 0.
№ 21
Опр. Логарифмом числа b по основанию а называется показатель степени, в
которую нужно возвести основание а, чтобыполучить число b.
Формулу
.
1. Сумма корней приведенного квадратного уравнения x2 + px +
q = 0 равна второму коэффициенту, взятому с противоположным знаком, а
произведение корней равно свободному члену, т.е. х1 + х2
= -р, а х1х2 = q .
2. Теорема, обратная теореме Виета. Если р, q, х1, х
2 таковы, что х1 + х2 = -р и х1х
2 = q , то х1 и х2 - корни уравнения x2
+ px + q = 0.
№ 21
Опр. Логарифмом числа b по основанию а называется показатель степени, в
которую нужно возвести основание а, чтобыполучить число b.
Формулу  (где b > 0, a > 0 и a (где b > 0, a > 0 и a  1) называют основным логарифмическим тождеством.
Свойства логарифмов: 1) называют основным логарифмическим тождеством.
Свойства логарифмов:
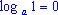 ; ; ; ;- Логарифм произведения равен сумме логарифмов сомножителей:
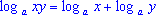 .
Для доказательства воспользуемся основным логарифмическим тождеством:
x = .
Для доказательства воспользуемся основным логарифмическим тождеством:
x =  , y = , y = 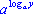 .
Перемножим почленно эти равенства, получаем:
xy = .
Перемножим почленно эти равенства, получаем:
xy =  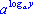 = = 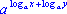 .
Следовательно, по определению логарифма (п.3) доказан. .
Следовательно, по определению логарифма (п.3) доказан. - Логарифм
частного равен логарифму делимого без логарифма делителя:
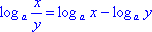 .
Ход доказательства аналогичен доказательству п.3 .
Ход доказательства аналогичен доказательству п.3 - Логарифм
степени равен произведению показателя степени на логарифм ее основания:
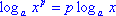 .
При доказательстве, также необходимо воспользоваться основным
логарифмическим тождеством. .
При доказательстве, также необходимо воспользоваться основным
логарифмическим тождеством.
№ 22
- Производной функции f(x) в точке х0 называется предел
отношения приращения
 функции в точке х0 к приращению
функции в точке х0 к приращению  аргумента, когда последнее стремится к нулю. Это можно записать так:
аргумента, когда последнее стремится к нулю. Это можно записать так: 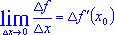 .
. - Из определения производной следует, что функция может иметь
производную в точке х0 только в том случае, если она определена
в некоторой окрестности точки х0, включая эту точку.
-
Необходимым условием существования производной функции в данной точке
является непрерывность функции в этой точке.
- Существование
производной функции f в точке х0 эквивалентно существованию
(невертикальной) касательной в точке (х0 ; f(х0))
графика, при этом угловой коэффициент касательной равен
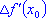 . В этом состоит геометрический смысл производной.
. В этом состоит геометрический смысл производной. -
Механический смысл производной f '(x) функции у = f(x) - это скорость
изменения функции в точке х. Поэтому при решении прикладных задач следует
помнить, что какой бы процесс ни описывался изучаемой функцией у = f(x)
производную с физической точки зрения можно представить как скорость, с
которой протекает процесс.
№ 23
- Производная суммы равна сумме производных, если они существуют:
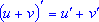 . . - Если
функция u и v дифференцируемы в точке х0 то их
производные дифференцируемы в этой точке и
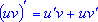 . . - Если
функция u и v дифференцируемы в точке х0, а
С - постоянная, то функция Cu дифференцируема в этой точке и
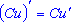 . . - Если
функция u и v дифференцируемы в точке х0 и
функция v не равна нулю в этой точке, то частное двух функций тоже
дифференцируемо в точке х0 и
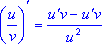 . .
|
|
|
|
|

 Ответ №2. Опр. Квадратичной функцией называется функция, которую можно
задать формулой вида y = ax2 + bx + c, где х - независимая
переменная, а, b и с - некоторые числа, причем а
Ответ №2. Опр. Квадратичной функцией называется функция, которую можно
задать формулой вида y = ax2 + bx + c, где х - независимая
переменная, а, b и с - некоторые числа, причем а  Ответ 3
Если переменная у обратно пропорциональна переменной х, то эта зависимость
выражается формулой
Ответ 3
Если переменная у обратно пропорциональна переменной х, то эта зависимость
выражается формулой  № 4. Опр. Функция, заданная формулой y = ax, где а - некоторое
положительное число, не равное еденице, называется показательной.
1. Функция y = ax при а>1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то ax > 1;
е) если х < 0, то 0< ax <1;
2. Функция y = ax при 0< а <1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0< ax <1;
е) если х < 0, то ax > 1.
№ 4. Опр. Функция, заданная формулой y = ax, где а - некоторое
положительное число, не равное еденице, называется показательной.
1. Функция y = ax при а>1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то ax > 1;
е) если х < 0, то 0< ax <1;
2. Функция y = ax при 0< а <1
а) область определения - множество всех действительных чисел;
б) множество значений - множество всех положительных чисел;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0< ax <1;
е) если х < 0, то ax > 1.

 №5.Опр. Функцию, заданную формулой y = loga x называют
логарифмической функцией с основанием а.
Свойства функции y = loga x при a>1:
а) D(f) = R+;
б) E(f) = R;
в) функция возрастает;
г) если x = 1, то loga x = 0;
д) если 0<x<1, то loga x < 0;
е) если x > 1, то loga x > 0.
Свойства функции y = loga x при 0<a<1:
а) D(f) = R+;
б) E(f) = R;
в) функция убывает;
г) если x = 1, то loga x = 0;
д) если 0 < x < 1, то loga x > 0;
е) если x > 1, то loga x < 0.
№5.Опр. Функцию, заданную формулой y = loga x называют
логарифмической функцией с основанием а.
Свойства функции y = loga x при a>1:
а) D(f) = R+;
б) E(f) = R;
в) функция возрастает;
г) если x = 1, то loga x = 0;
д) если 0<x<1, то loga x < 0;
е) если x > 1, то loga x > 0.
Свойства функции y = loga x при 0<a<1:
а) D(f) = R+;
б) E(f) = R;
в) функция убывает;
г) если x = 1, то loga x = 0;
д) если 0 < x < 1, то loga x > 0;
е) если x > 1, то loga x < 0.
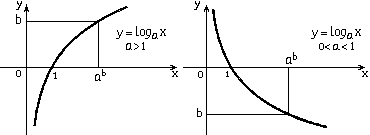 №6. Опр. Отношение катета прямоугольного треугольника, противолежащего
острому углу, к гипотенузе называется синусом этого угла (обозначается sin
№6. Опр. Отношение катета прямоугольного треугольника, противолежащего
острому углу, к гипотенузе называется синусом этого угла (обозначается sin  №8.Опр. Отношение катета, противолежащего острому углу прямоугольного
треугольника, к катету, прилежащему к этому углу, называется тангенсом
(обозначается tg
№8.Опр. Отношение катета, противолежащего острому углу прямоугольного
треугольника, к катету, прилежащему к этому углу, называется тангенсом
(обозначается tg  №9.Опр. Отношение катета, прилежащего острому углу прямоугольного
треугольника, к катету, противолежащему к этому углу, называется котангенсом
(обозначается ctg
№9.Опр. Отношение катета, прилежащего острому углу прямоугольного
треугольника, к катету, противолежащему к этому углу, называется котангенсом
(обозначается ctg  Ответ № 10
Ответ № 10

 Рис.1 Рис.2
Повернем радиус ОА, равный R, около точки О на угол
Рис.1 Рис.2
Повернем радиус ОА, равный R, около точки О на угол 