|
|
|
|
Диплом: К решению нелинейных вариационных задач
~t< О О Сл - Га. О О Сз -t3 |
(3')
где с/= а^ с, = а^ - ^-i-, А^-^л ^ = & + "^"г"
Тогда алгоритм решения системы (2) представим в виде алгоритма:
1. {,-- 2-Lp^ I, =<?-^; ft/ - ^^)/i,, О. = ^-^^/^,
i^^+kp,)/^, ^--(^^p.)/^; ^^-^4^ ^=-^^//.;
(4)
2. e/--ft<, с^о,- -1^ ^=^,
з: ^-< -. f<a<,^ -^ г:л-г ^) /с^ ;
У^ = (о1^ ^ ^^ ^+,^)/Сп-г > ^ ^ ^ з/..., о-i.
Алгоритм называется корректным, если все действия в нем выполнены, т.е. ^
^о, U i-0 / G.f =<?, CiTt-o . Устойчивость
алгоритма обуславливается выполнением условия ; Уп-ч, = •с^Н/^/-'1
^ '^/Сп-^ , |^>-(;/Ся-<: I ^ ^ . Нетрудно видеть, если исходное
уравнение (1) нелинейное, то система типа (2) также будет нелинейной, а
алгоритмы типа (4) составить невозможно.
^ .- Рассмотрим примеры решения краевых задач для дифференциаль-'HbDF'BTOporo
порядка с переменными коэффициентами, где как правило аналитических решений
не существует.
Пример!.
Дана краевая задача: i/"^- 2^ ^ ^и--= s^ft эс. Ч'(о)=- О, ^ ('/) '= 3
. Результаты вычисления этой задачи по алгоритму (4) получим в виде
таблично заданной функции.
| 5СГ | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0.7 | 0,8 | 0,9 | 1 | {^ | 0 | | 0,79 | | 1,59 | | 2,32 | | 2,94 | | 3 | | ^ | о | 0,38 | 0,76 | 1,13 | 1,49 | 1,82 | 2,13 | 2,41 | 2,65 | 2,85 | 3 |
32
III. ПОНЯТИЕ ОБ ОДНОМЕРНОЙ ВАРИАЦИОННОЙ ЗАДАЧЕ
Исходя из общего закона сохранения энергии многие физические задачи при
адекватном построении их математических моделей сводятся к вариационным
задачам. Вариационное исчисление занимается задачей отыскания наибольших и
наименьших значений функционалов.
3.1. Постановка простейшей задачи
Задача состоит в определении функции и •=. •? ('>-) ,
которая сообщает экстремальное значение некоторой величины У= ^У^у7 ,
т.е. функционала, ^г.
Предположим, что ^ J р ^ у. /) ^ ^
7<
^х'^^; ^^ (1)
где г (. эе/ у, ^/ - заданная функция, и а - заданные числа.
У^
Различным кривым ц : и [ ^е.) , проходящим через граничные точки С
эс<; ^ ) и (^л.', Уи.) , будут отвечать различные величины.
Определим такую функцию у ^ i/ С^) , для которой ^ i-
^'('^У'^ , т.е. функционал принимает максимальное или минимальное значение.
Далее будем рассматривать задачу только на минимальное значение
УГ^'(>)], т.е. будем искать такую функцию у= уЛ^ , чтобы было
Н^(^).] '- ^п- ^Су(^)] ^ Л3^ Х^Х^ . Например, для задачи
п^- JYy'^ ^х, ^о)--о, ум^ (&)
/ функции i/ =- х. , ol 6r [p, будут удовлетворять условиям :
ylo)^o, ^}--L
При этом .,
г / ^
У г,. ^ - Я U^) ^ ^)^. ^ ^ ^-. fU).
33
задача свелась к нахождению минимума обычной функции -fW:
n'J) - ^^°6 А__ /,
\{^~~^^~ ~^^ ^0 -
(^^)(^1)^-2-(2^-Y)^0 ^
U -г) (^3^ з^ ^ з^ + /) ^о -7 о^ = ^.
Нетрудно показать, что при +{2) ^ /^-п г(0^/ ^ Итак, ь.^
-УГ^-^^,-^0^ ^^> ^ З";
решение задачи будет: и=- ое^' Рассмотрим семейство кривых (см.рис.8):
у f^ jc^ = y^ + с/. ^ ^ , где ^ ^ -произвольная функция, но ц
(зе^)^ И (v.s.}~-C> (см .рис. 9).
'.(
-
i A
Тогда при малых об для кривых L/(o[^oc,) интеграл (1) будет принимать
значения близкие к минимальному и зависит от параметра^:
.Vi
(з)
Если мы предположим, что функция у^ доставляет минимум J^v, то необходимое
условие минимума будет: ^/,
oL-JW
^^ ^
Продифференцируем (3) по Л:
dl. ? d^d-r,- Тг C)F •^ ^ эр •^7,/
~си ~ J ^г^-J l &r й-+ у cSrJ^ ~-
я< yf q v
~- t^rt^rt'^-
34
Имеем:
.Г;. ^
JVt>^- i^^
Л'« JC< -ха /2г
- Fn' • v ^ - ( ^
Поэтому:
^ - ( Г F' ^ F' 7 и/ )У
^^-J Lf^^^J^)^-
л/
-h^ri.-^^^o ®.
'VI.
/ ®
Законность перехода —-^ обуславливает следующая основная лемма
вариационного исчисления:
Если Ф(^) , ^) непрерывны на JZ У<; % 7
и^Н^-^ то из
У
J^?^^A^--^
вытекает, что ^(ус) = <9 при ^ ^ у ^ СР^ .
35
В нашем случае: р^у^ч- ^и , pi,/ -- ^у , поэтому и получим с. _ сл . с,/ = О ^ ^ - -^г (о-^')^ и"^ л. ^у'^^х+^ , ц^ л^е^^-с^ ; уо).о^Го^^^^ , ^-^=о ^(<)=.t Z^^ ^ + ^=3 отсюда у = ^ - решение. Таким образом, наше решение совпадает с решением полученном из самого определения минимума функционала. Следует подчеркнуть, что решение краевой задачи (5) не является тривиальным и разработка методов решения вариационной задачи (1) весьма актуальна. |
Доказательство (от противного). _ _ Пусть ^(^^О ^
^(^)7У>0 при Л^^ж^з^
ПОЛОЖИМ ({X.- Зй)^^- Хг) ^ "Р" Зс/^ Зе^. Д^
^ (9С-) = ^ о при Xf ^ зе^-
ДС,,, L у 5с-^ 5с ^ ^.
—t.
Тогда по свойству интегралов [ g>^L [^olx. >0
У.-1
вопреки допущению. Значит ^Р ( ^,) = О. Итак, мы пришли к следующему
утверждению:
задача (1) эквивалентна краевой задаче:
^'-^ /У= ° ' ^)^ ^)^ , . (5)
Дифференциальное уравнение /•?/ - ^' F^' ~ u
носит название Эйлера-Лангранжа.
Решим пример (2), сводя к краевой задаче (5). ,ii . //// t:' - о,/^
Примеры аналитического решения вариационных задач
f!/l
1) ^ у. / Су-\у' -7^ - о. ^о)= о. ^W- i -
Составим уравнение Эйлера-Лангранжа:
~^-^'^-°- -^~У-° - ^-/ -
и^^и^О ^ Lf ^ C^-w эе^ gl ^ ^;
ffo )= О СО, • c^-s 0+ ^ -Л fi о = О Г ^ _
^№)^ " lc. ш^^(^-^%^1 ^ 1 e^i
Ответ: (у -. St-^i X.
2) ^;'- J ^^ •^/г J^ ^ у^'^' ^ ^;= 6)
^ - (F^L -о ^ ^"^6^ ^^"^б^-о ->
/ • \ t -7->-^~' ^=о - t ^-о 'Lс^^^ |
и-.- х-^+Сгзс-t- G. ;
{^(^)^ (-f-C^C^-f \_^(о):о л- L а-о
Ответ: и = -х3
3) ^у- / (^у-^^ ^^ ^•^--^•
^-^')^о - ' ^^^-.^--^^.^^ f^)^ ГС^ . , ,
Г^г - [с^^ ' cf-^^
Ответ: Ут^1^^,
-f
4) ^У" J (^-^^)d^,
^(^)--^ ^(^)--^
^^v^0 ^ ^^-2Э=^- ^-^-^^^^^ ;
^f-/)=^ ^' ^^-^= ^ ^-i ^[^/6 ^^^^ "
^ - %
р - /-^
и ^ о
Ответ: У^ - ^Уе -* % л 5) о .
^TyJ 'J (У-i'^Jc/x ; ^-i)--0,y[o)-Z .
fy - (Fy'J^O ^ y'^x^o ^ a—^/e-'-^Kft't ;
r и(-i)^o f^ _ с, +U ^о
i^^ 'с . о^ -7
Г^ - ^/6
Lu ' ^
Ответ: ^ -»%+ ^^^
б) dC^-- j "А (у' ^у/А / ^= /, ^/^Д Г^/г
^- ^^ - -^^-^^
^ (^ й^-г ^-^ С( • ^/г X. ;
^[о)-- у ^f^- CUS^^O •^•/г6?- ^ ^)-% ^ L^- ^^-^-^
ft-^, C^~-o
Ответ 1/' - (^^" % 7) ^ У - ] if . 4у^^ , yfo)-e i, ^ /.
Уравнение Эйлера-Лангранжа:
^/,и^о^ fy^^y ^y^^e^^Qe
е^ f^e^e^^ Г^-^
38 2(f-^
Ответ: ^ е щ 8) ^у= / ^--^^ , ^о)-^(^)-0
Л/ - f^^ = о ^ с/ ^У^ 0 •=> у= ^ ^J ^ ^ ^/1- ^ 7
С и{о)^ о . С С^- cpso 1- ^-^по-^о i ч (^ )^о ^ I ^ • с^злП^ G • si^s. /7= о
С ') Р L { = и '> (- д. _ произвольное
Ответ: и ^ d ^п. х- - множество решений.
39
3.2. Метод Эйлера в вариационной задаче
Основоположником конечно-разностного метода в вариационном исчислении
является Леонард Эйлер. Однако, в связи с громоздкими вычислениями, которые
требует данный метод, до изобретения ЭВМ он не получил широкого применения.
Лишь компьютерная революция в математике способствовала широкому внедрению
метода Эйлера, и в настоящее время разные модификации его получили
распространение в прикладной математике.
Пусть дана простейшая вариационная задача: найти экстремум функционала
^
^£^)] - jf f^y,^)^
yf^)-^. ^/(^)-у^.
т.е. здесь надо найти такую кривую у С^) -, чтобы
^п: ^Г^;7= yCyW3 .
По методу Эйлера разобьем интервал Гль^З на П. частей точками (см.рис.
II): , ^ з^-^ Л^^ ЛЬ-^^ , ^= <2,...,
гъ ^ h- ~ ^
Необходимо найти ординаты у/,.. -, 4)- < соответствующие точкам х'/ i' /
--"-/, .,. , J^.n.-< •
Таким образом, искомую' функцию ^(^-} ищем в табличной форме:
| ое | До | ^ | 1 | '-<?«.- -f | У <--<,ц, | | ^ | ^ | ^ | 1 ' 1 | ^ | ^ |
uf^\~ ^l(^)-^) ^^^
У 1 / ——И——— " ~И—— '
интеграл (1) заменим суммой:
Зчт. п-f
^1^']р(^')^^Г(л^, ^^).L --
— лл
t
^ J J
- Ф^-^-J
40
Ординаты У/, ..., j//i-/ выбирают так, чтобы функция 9? (у^ •, ^-/ У
достигла экстремума ( как функция л---/ переменных У-/,-•• ^-•r ),
т.е. находятся из условия:
9(р - о - ' ^^ - О . ^ ' •" ; ^ "" |
б)^
^0 ;
/ ^Р ( Ъ^
В целях достижения достаточной точности число /I | берут до- | | вольно большим. При этом приходится решать систему типа | (3)с n-f | | неизвестными, т.е. высокого порядка. | | | | ^ | | | | | •i1 | \ | | | | | | | | | | ^ | .'^/ | | | | | | Ч-- | 'л | г г - | | | ^- | | I/t• | | | -X'o 3-i ЗСд, Эе,- Jc't'+i' ^ , Рис. 11 | Гк Я1. |
Пример. Найти приближенное решение задачи о минимуме функционала ^
^J-J^+^b^^e, ^(oY--^^)--O
0 f /,<9 Решение. Возьмем Л = ~~s~ ^ °/^ и положим
^-^о)-0 ; ^^(^2); ^-^(О^),
^-^°^ ^--Ц1°^^ ^-:^~-0• Значения производных приближенно заменим по формуле
^•-^'(v^)к ^^ ^-
Тогда
41
t/ у/п /'} - ^-^
; ^^Л -^2-
,7 - I -/ - ^ . ^ ^ Данный интеграл заменяем суммой по формуле прямоугольников
"S-f^d^ ^ с ^o.}+^)^^^^)']-k
Будем иметьа' щ-w'.) <^-/^ (о^ ^•°)^ (W^y^- ^ -. (^)^^S.^ . (^L)^^ ^-^ ^ |
Будем иметь а-
-+
Составляем систему уравнений для определения ^ ^ ^ /Л, искомой ломаной:
^н^' 2(^'OJ•/ ^ -^^^^"^^'^^ ^^0
^ '-[(^•д ^^/ +^•г^^X^+ ^.г.^ •^ -о
•^гГ^•г^-^/+^^-м^+^^'
^L7г=o. ^-f^'^-^-^^'^^^'^^ ^
<7 \ у ( ^л^.
и^л- •9^-^---^
^^^^ "-^ -=~^о^ ^ -Ь ^,00^^ - ^
= -0,0^
- ^ -+ ^^ -^ , .о^
-^ + S,00i{^ = - ^0^!L ^
у^^^т; ^--^w; у^о^^^. ^ о,^ш.
___т.е.________________________________________
| Х | о | 0,2 | 0,4 | 0,6 | 0,8 | 1 | | ^ | о | 0,132 | 0,273 | 0,402 | 0,522 | 0 |
Точное решение исходной задачи:
^TS^^; ^~ (^ ~c' ~ ^"-у^-^
Тогда решение краевой задачи
/Sri%- ^f0^^ ^^0
42
будет: u(r)^(eл-ix)-e/(^-ei)+x.^-q^6sя.(e!^e^)•^
Приведем сравнительную таблицу:'
У | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | | ^ | 0 | 0,13712 | 0,27341 | 0,40211 | 0,52231 | 0 | | ^- | о | 0,13693 | 0,27142 | 0,40071 | 0,52199 | 0 |
Таким образом метод Эйлера дает весьма удовлетворительные результаты в
смысле точности.
Рассмотрим случай п. ~? оо в методе Эйлера.
Из(2)имеем: ф (^„...,у^) ^- { F ^-^ЗД +." + +F (Г^, ^, ^^^F(^,y., ^-)^„^^(Х^,^,
^^%}]. Тогда система (3) для определения ^ , ^ , ..., i/^-f будет:
1^^^ k-[0^^o^F^-^ ^^, +Fy^(~/^io^o
-^-^/^^^J-^^^^-^J;//^
Переходя к пределу при /l-> po , получим уравнение Эйлера
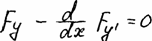которому должна удовлетворять искомая функция у/х.), реализующая
экстремум. Аналогично может быть получено основное необходимое условие
экстремума в других вариационных задачах.
43
3.3. Алгоритм решения линейной вариационной задачи
Рассмотрим задачу:
Найти ivbin. У tu 3 , где
^ <7
^M--j {^^^^^(^^W-^)^. <J Уо v
у/^^, ^(%^)--^ (1)
Имеем: ^>i-[ [ {^^^^^-IW^-^
^ ^.y/J.,,.[(^L/.^^^.^.^JJ =9^,,^
(2) где ^ . ^(^), fc - W,- К- ^(^)-
Условие минимума ^ , т.е. /э<^ ^О будет:
г0^-^ = ^
-^^ал^-^ = &
-^0^-^ = ^.з (3)
^ '^-^ •+а^^^ -^ = &^ где 0;=^^/.;
(с-^Л -^^) ,S^^~^^ ' ^ ^-^'^-^ & --^. Л--^^. ^-^
После элементарных преобразований система (3) примет вид:
^^ "^ = '^ ^-ys ~ ^
С^^ уа-ц - ^•г ^ oi^-i.
Сп-у Un--f = ctfi-f где Ci^a, ^ c^^CUi-f--^- ; cl^&, ;
^= &./ + ^- , е./^.-^-^
L-<.
44
Решение системы (3') запишется в виде:
^ . ^- , ^ -. oL_.J^-^ (4)
(7 Cn.-^ u Cn-c ^=-^- ./ ^-S..
Итак, решение задачи (1) сводилось к последовательным вычислениям по
следующему алгоритму:
1. 0,=.?+A-^ ; йг^^Л. ; 0^=^^^ ;
g^-^ ; &=-^^ ; ^^-^^-. ;
Л i (5)
2. c^ai ; (\-а^--^- ; c^^a^^f --сг ;
л-с^ ; л^^4- ;^-^-^-;
_ (?6л-^ • и, ^ 6^/»-^ + ,9^^Л-с • •- — ———————— 5 ^Д-< ~ ———————————tt-————————- 1 L- ~ |
3 Г/ - С^-< • и- - Oif-^ ^ ^f>^(~<-_ • . - о <.
л _о ^-<-^r75^-——^———.с--.2^..,лА ,
Этот алгоритм будет корректным при Он ^ О , С^ /^ С? ; устойчивым при ^
> / . Рассмотрим примеры решения вариационных задач по алгоритму (5)
(см.приложение 2).
45
3.4. Понятие о методе Ритца
Проиллюстрируем идею метода на простом примере ( этот пример не имеет
аналитического решения). Пусть ищется минимум функционала:
^
У^-М -f (у^ x у)^ W
О
при краевых условиях
'о)-О ; у/О^/ (2)
Приближенное значение будем искать в виде:
^-.x^^-^(^-x)^„,^C^x^(^-^).
При этом первое слагаемое всегда удовлетворяет краевым условиям (2), а остальные
слагаемые удовлетворяют однородным краевым условиям
у^)=с^^'^=б>,такчтовсясумма ^= х-^-С^зс^-^)ч- „,+ С^Л Y/~^
</ так же удовлетворяет краевым условиям (2).
Рассмотрим решение при n^f, т.е. решение ищем в виде Ч^ х+ ^^{f~'x-)•
Тогда подстановка его в (1) дает:
^- J [ (^ (^)}^ ^(эс + ^ое- С. ое г) 'J^ . о
Г f ^ С, ~ ^ (^ ^)эе + ^ С^эе. i ч- f^^/^--^С. (^ С^^ ^ ^ ^Лос--^ (^ С,) ^
-1^{^с^).^с^-^)^
-Чтобы найти минимум этой функции, приравняем к нулю произвол-
ную ^ -1- (^) - ^(^С,). ^- Сг - о ^
С/ = -0,0 70 f-Р.
46
Тогда решение (1) в первом приближении будет:
и-, х- - о, о У е^де (^-^) = о, ^w^-x^ О, 9£ <^ л- ^ ^
В общем случае для двуточечной вариационной задачи
? J'-JF ^ ^ ')с(^ ; ^).А ^г)- 6 о)
а-приближенное значение можно искать в виде:
u-fy ^ J^L^)^ ^-а)[с^-ё)...^ ^ ^-S) 'J (4)
(j f) ~0-
Итак, основная идея метода Ритца заключается в том, что искомая функция
ищется в виде, включаемой несколько произвольных постоянных (параметров) ^ :
у. ^ (^е^с.,.^Сп.) (5)
При этом правая часть S^f^ ^/,. , Сл.) выбирается так, чтобы для любых
Ci удовлетворялись граничные условия:
^) - ^(л, С.,.., и.) = / , ^)- ^ С/,.., и. ; ° 6.
Подставляя (5) в функционал (3) получаем функцию от неизвестных С^, Сз.,---,
Сп,'.
^J^x^f^,..,^)^ ^ (^е.,.., (^)о(^ - ^,... ^
о'
Тем самым задача об экстремуме функционала сводится к задаче об экстремуме
функции от п. независимых параметров ^ ^ ... ^ С^ .
47
3.5. Примеры решения вариационных задач методом Ритца
1) Найти решение вариационной задачи:
•у^ -1 d/' ^"+ ^у)^ •' у ^ °- ^-0 •?-
Ищем решение в виде: ^ •= с^ Х.(^~ ^ )'= °<^ ( л'- х- J • .^—^-r ''•^(i-
Ул* -- v- /
л - -» /* . 1
П . / Л -t ^ '^ Л
Тогда ^ j , П^Y/^- ^Y^-z^^^^^-^^J^ -
/. " о ^Jf^Y/^a-^a^^^ai^-a^^^^^^it^J^ .
-0^^^-^;. ^ -^/^^ ^-^-Отсюда и^ = - s (ус- ^)^ и-(^
Найдем точное решение: /^ - (f^') = 6?^^/ ^У ^ :у "=> ty= ^ с<?^ зе ^ <1 Sc^ ае ^ ^
^)^ .Г^-0 -{^=^/
у^^О iCrC^^i-Ci^n^-f^O U\--/scn^ у^= ^е- ^^/
Приведем сравнительный анализ численных результатов:
| Л! | 0 | 0,25 | 0,5 | 0,75 | 1 | | ^ | о | -0,044 | -0,070 | -0,060 | 0 | /р; | о | -0,052 | -0,069 | -0,052 | 0 |
2) Найти решение нелинейной вариационной задачи:
yf^ j -- 7 //i-^}^, ^> ^ ^)- ^
Будем искать решение в виде:
- у^ ^ ^- За: ^^ /^-^^ В такой форме она удовлетворяет краевым условиям:
f ^ ^= ^3-^^^/^-^'У^^ L ^ [i) -^-з-^ ^ff-^)- ^
48
Имеем: ^
y^J=7/^^'^-3J^ ^-^-.^'-^J ]^-
о -Откуда:
М^Й- = {(^^)^E^f^)-^3 ^ 5-fx-^E ^ -^ ^
^оГГ^ L ,
^ ^^~x9J }А=о - ^f^^ffo^f +^0^o-^^-^^
Решение ^/^ = 5,^/3^^- ^^/-Зд:^^ -= 4^-3 г -з,о^/3^--г^
| г^ | О | 0,25 | 0,5 | 0,75 | 1 | ^ | 4 | 2,6798 | 1,7397 | 1,1798 | 1 | ^^-Зг. | 4 | 3,2500 | 2,5000 | 1,7500 | 1 |
^
Пока о достоверности решения у /• /а^) судить очень трудно, необходимы
более высокие приближения.
3) Найти решение вариационной задачи
н^у] -JY.?v^v^, yfo)^)-o.
С?
Точное решение:
Р = J?JC.Vi- U
^-^/' ^-^//^
Общее решение: у "= ^ (? -i- Cx.o. Из условий ufo)-=^ , и^^у^о
е,- -1—— --^
Тогда точное решение задачи будет:
49
/7)Е fb ^w-л - ^^^'- e~x;- ^ •
Методом Ритца в первом приближении решение ищем в виде:
<у= ех(^-ус)-. с(^м-^), у^е^-^^};
7r^j=JС c(^^^^з)+aC^'-^з>^^^^-^ -.^jj<^- %c^^a^^^};
(р^с)-^^^ ^у^е^о ^ с^-^.
Итак решение по Ритцу:
^-i-^
Сравнительная таблица имеет вид:
Л. | 0 | 0,5 | 1 | 1,5 | 2 | у^ | 0 | -0,275 | -0,3571 | -0,2758 | 0 | ^г) | о | -0,2126 | -0,3520 | -0,3258 | 0 |
50
3.6. Об одном подходе к решению нелинейных вариационных задач
В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче
зададим в виде:
r-^^f^-^^
При этом граничные условия и{а ) = А, ^• (б/=- /З выполняются, а ^
является искомым параметром. Решим этим методом пример из пункта 3.3.
Имеем:
Г-°\^ ^ - х ^е - ^j ]Т^)^Г^-^^^^ -j^-w
л/
Минимальное значение функционала J соответствует минимальному значению
функции У/о^ . Найдем /^»г- •f(<jL) :
pi fi}-rAU\' + ( -L_}' - ^=^L - J:__ .п ^ <^-Ь^-/^' [^^М ~ ^о/-/;^ (л^)^ ~~0^
(^ ^^)(^)^(&^)^^\^^^^/^-^ п
Так как -^^У^^/^^и A f^V^ -^W^<9 то корень уравнения нахо-дится в промежутке
[1;1Д]. Представим (*) в виде </=с/-^ ^ -f^f^^^M из условия
fttd)c(^W)^ ^ ^X^/,'f получим С. =-0,01.
Поэтому сходящийся алгоритм будет:
с4 ^ = о4 - оо< (((( ^ i-^)^ ~ ^)^ - ^4 - /) ^
Берем Лу =1,05 и по формуле {**) последовательно вычислим о/<
=1,04256,....., ^=1,03004, о4=1,02991, с/^= 1,02990. Поэтому примем ц/^ 1,0299
^1,03; тогда решение будет:
^а.^е^^^
51
Решение по предложенному методу и методу Ритца почти совпадают:
| 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | | 0 | 0,2111 | 0,4166 | 06166 | 0,8111 | 1 | | 0 | 0,1906 | 0,3902 | 0,5968 | 0,7981 | 1 |
Итак, предложенный подход к решению задач может быть применен, т.е. ему
посильны и нелинейные задачи.
В частности, рассматривая нелинейную вариационную задачу на
отыскание ги-^ п- функционала
^/-
У /У^А7 - / f/^ ^y)ol^
с краевыми условиями ^/о^= с? ; у /"•/) -= У ;
будем отыскивать решение на кривой ^ -^ ^ ^ . Тогда функцио
нал примет вид:
У-J/: (J, ^-') \ я^^^/Г^-г:^ х. ^JA =
.f^^L, ^ W-с^^.,W ( ^-^ -й^-7/д if.i.ci-')
и задача об определении его л^л. сводится к отысканию пъС ^1{oi)
га). ^=^,. ^ -^ - ^; т - ^,
-Г(^)^; f"(^)^o:
Поэтому при</= 11^- //<4/примет наименьшее значение на
кривой и-, r^^-wm g ^^ у , азначение ^ ^/^1^1,183.
52
3.7. К методу Ритца для двумерных задач
Для функционала •^- ^J '( v-' ^ ^^Р^)^ <^
уравнение Эйлера- Лагранжа примут вид:
JiL-iL^l-.-S-/2L ^ ъг-ъг ъ^\ър) осЛм / 5где ?~ эх '
^ ^-? = ^ •
Пусть ищется экстремум функционала
f[:iC^n-J[h^^- г<^-?^4 .средифунк-ций, обращающих в нуль на границе
квадрата, ограниченного прямыми dc^^-f •> с/ = ± d • При
этом мы приходим по существу к задаче Дирихле для уравнения Пуассона ^ у.
у- i^y ="У С^^}^
г^;Г^г^/;/^ ^/;-/^г^-/;~/;=<9 (см.рис.12)
Эта классическая задача не решается | точно с помощью элементарных
функций. Приближенное решение ищем при ^(у/^)~=^ —<
———— ———*77"^.
по методу Ритца в виде i-i ^f^~^)('f~^2'} Подстановка в
исходный функционал дает •
f^f[W(^ ^^Г. ^ ^.г.с(^х^}}Л^. ^j-^ ^с^-Г^)
Тогда Г1^)-^-^С- ^---0- С--^ :
ПФ^-^о, ^ у ^ й=-^, u—ig(^)W
решение задачи при первом приближении.
Сравнение с точной формулой (имеющий вид бесконечного ряда) показывает, что
погрешность этого приближенного решения в среднем равна 1,5%, а погрешность в
значении функционала около 0,2%. Таким образом, идея метода Ритца
распространяется для двумерных (и, вообще, для многомерных) задач.
53
ЗАКЛЮЧЕНИЕ
Дипломная работа посвящена методам решения экстремальных задач, при этом
приведены основные идеи различных методов, которые почти совсем не
рассматриваются в школьном и педвузовском курсе математики. Таким образом,
заполнен существенный пробел в математическом образовании и подготовлен
материал для изучения основ современной прикладной математики в классах с
углубленным изучением математики.
Основные выводы по дипломной работе:
1. В краткой реферативной форме изложены элементарные методы решения
экстремальных задач, основанные на известных неравенствах типа Коши.
2. Приведены основные идеи методики решения задач математического
программирования: три разновидности задач линейного программирования,
принципиально различные примеры решения задач нелинейного программирования.
3. Изложены методы решения двухточечной краевой задачи; дан вывод
сходящегося алгоритма и на его основе решены на ЭВМ ряд линейных задач с
переменными коэффициентами.
4. Излагается вариационная задача с выводом уравнений Эйлера-Лагранжа и на их
основе приводятся примеры аналитического решения. На основе идей метода
конечных разностей получен алгоритм для линейной вариационной задачи и на его
основе решены ряд вариационных азадач на ЭВМ; результаты приведены в
приложениях.
5. Методом Ритца решены ряд нелинейных задач, одна двумерная задача. На
основе решения модельных задач подтверждается достоверность полученных
результатов.
6. Приведена новая модификация метода Ритца, для которой нелинейность
вариационной задачи не вызывает особых затруднений.
ЛИТЕРАТУРА
1. Алгебра и начала анализа 10-11 кл., М., 1992.
2. Белман Р., Калаба Р. Квазилинеоризация и нелинейные краевые задачи. "Мир",
М., 1968.
3. Блох В.И. Теория упругости. Харьков, изд-во ХГУ, 1964.
4. Буслаева И.П. Решение задач без использования производной. Математика в
школе № 5 -1995.
5. Возняк Г.М., Гусев В.А. Прикладные задачи на экстремумы. М., 1985,
"Просвещение".
6. Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в упражнениях и
задачах. М., "Высшая школа", 1986.
7. Демидович Б.П., Марои И.А., Шувалова Э.З. Численные методы анализа. М.,
"Наука", 1967.
8. Дородницын А.Р. Применение малого параметра к численному решению
дифференциальных уравнений. В книге "Современные проблемы систематической
физики и вычислительной математики". "Наука", М., ^ 1982.
9. Камке Э. Справочник по обыкновенным дифференциальным уравне-« ниям
.- "Наука", М., 1972.
10. Краснов М.Л., Макаренко Г.И., Киселев А.И. Вариационное исчисление.
"Наука", М., 1967.
11. Курант Р. Курс дифференциального и интегрального исчисления. "Наука", М.,
1967.
12. Матвеев И.М. Дифференциальные уравнения. "Наука", 1970.
13. Мышкис А.Д. Лекции по высшей математике ."Наука", М., 1969.
14. Сайфуллин Э.Г., Саченков А.В., Тимербаев P.M. Основные уравнения теории
упругости в напряжениях и перемещениях. Сборник исследований по теории
пластин и оболочек, в. 18, часть 1. Казань, Изд. КТУ, 1985.
15. Соминский И.С. Элементарная алгебра. Дополнительный курс. Физ-матгиз, М.,
1969.
16. Циаф Л.Я. Вариационное исчисление и интегральные уравнения.
"Наука", 1970г.
t„ 17. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное
исчисление. "Наука", 1969.
• ^. "
HWUA-cA^ /^1СЛ^И-1с^«^-''1Д.
program diplomi; 4.
uses graph,crt;
label 1;
const n=200;
type mas=array[0 ..n]of real;
var a,b,c,d,f,y,p,xx,l,r,g: mas;
j,z,x,h: real;e: char;
i,j1,il: integer;
ff:text;
procedure vap(var xx,y : mas) ; клил-ели.^- бор-с.(,ои/^с^<^о^
var x,h: real; i: integer; ' ^с^-оли,
a,b,с,d,f,p:mas;
begin
h: = 2/n; x: =1;
for i: =0 to n do
begin
f[i]:= exp(-x*x) ;
p[i]: = cos(x*x);
xx[i]: =x;
x: =x+h end;
УСО].- =0;y[n]: =4;
for i: =1 to n do a[i]:=2+h*h*f[i];
b[l]:=y[0]-h*h*p[l];
b[n-l]: =y[n]-h*h*p[n-l];
for i: =2 to n-2 do b[i]: =-h*h*p[i];
c[l]: =a[l]; d[l]: =b[l];
for i:=2 to n-1 do
begin
c[i3: =a[i]-l/c[i-l];
d[i]: =b[i]+d[i-l]/c[i-l];
yCn^l]: =d[n-l]/c[n-l];
for i:=2 to n-1 do
y[n-i]: =(d[n-I]+y[n-i+l])/c[n-i];
end ;
procedure kr( var xx,y :mas); ьтшлмлла ^Uscuiocd
\gjqcuwl var x,h: real;!: integer; '
v v a,b,c,d,l,r,p,g,f: mas;
begin
h: =l/n; x: =0;
for i: =0 to n do begin
p[i]: =2*x;
g[i]: =x*x;
f[i]: =sin(x*x);
xx[i]: =x;
x: =x+h;
У[0]: =0;y[N]: =3;b[l]: =y[0]-2*h*h*f[l]/lCl];
cCl]: =a[l];d[l]: =b[l];
for i: =1 to n-1 do begin 1[i]: =2-h*p[i];
a[i]: =(4-2*h*h*g[i])/l[i];
r[i]: =(2+h*p[i])/l[i];
end;
for i: =2 to n-1 do begin c[i]: =a[i]-<r[i-l]/c[i-l]);
b[i]: =-2*h*h*f[i]/l[i];
d[i]: =b[i]+(d[i-l]/c[i-l]);
end;
for i: =1 to n-1 do
у [n-i]: =<d[n-i]+r[n-i]*y[n-i+l])/c[n-i];
end;
begin il: =detect;initgraph(il,j1,'' );
assign(ff,' b: reseda, dip' ); <2. rewrite(ff);
1: cirscr; settextstyle(0,0,2);
outtextxy(300,80,'МЕНЮ: ' );
outtextxy(135,150,'1.РЕШЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ.');
outtextxy(135,200,'2. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.'):
outtextxy<135,250,'3. КОНЕЦ . ' );
outtextxy(145,350, 'ВЫБЕРИТЕ НУЖНЫЙ ПУНКТ МЕНЮ .');
Е: =READKEY; •
case e of ' Г: begin
cirscr;settextstyle(0,0,3);
outtextxy(100,40,'РЕШЕНИЕ ВАРИАЦИОННОЙ' );
outtextxy(250,80,'ЗАДАЧИ' );
settextstyle(0,0,2);
outtextxy(155,130,'Дана вариационная задача:');
outtextxy(145,200,' I(Y)= ( y+2cos(x)y+e y )dx');
settextstyle(0,0,4);outtextxy(230,190,'S');
settextstyle(0,0,2);
outtextxy(200,280,' y(l)=0 , у(3)=4 ');
settextstyle(0,0,2);
outtextxy(240,170,' Г );outtextxy(235,225,'3');
SETTEXTSTYLE(0,0,1);
outtextxy(329,190,'2');
settextstyle(0,0,2);outtextxy(315,180,',');
settextstyle(0,0,1);
outtextxy(440,190/ 2');
outtextxy(500,190,'-x');outtextxy(520,185,'2');
vap(xx,y); writein;
writeln(ff,' РЕШЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ' )
writeln(ff);writeln(fr);i: =0;
while i<=n do begin
if i<=n then
writeln(ff, ' ' ,xx[i]: 1: 3,' \ ',y[i]:l:3, ',xx[i+l]: 1: 3,'
',y[i+l]:1:3)
© 1 S6
writeln(ff,' ' ,xx[i]: 1: 3,' -,y[i]:l:3);
i: =i+2; end;
e: =readkey; goto 1; end;
'2': begin
cirscr; SETTEXTSTYLE(0,0,3);
OUTTEXTXY( 50, 80, '-РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.');
settextstyle(0,0,2);
OUTTEXTXY(150,130,'Дана краевая задача: ');
OUTTEXTXY(145,200,'y+2xy+xy=sinx ' );
OUTTEXTXY(150,280,' y(0)=0 , у(1)=3 ');
OUTTEXTXY(152,180,' ,,' );
OUTTEXTXY(218,180,' ,' );settextstyle(0,0,1);
OUTTEXTXY(255,190,'2' );
outtextxy(350,190,'2');
kr(xx,y); writein;
writeln(ff,' РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ' );
writeln(ff);writeln(ff);i: =0;
while i<=n do begin
if i<=n then
writeln(ff,' ',xx[i]: 1: 3,' ',y[i]: 1: 3,
',xx[i+l]: 1: 3,' ' ,y[i+l]: 1: 3) else
writeln(ff,' ' ,xx[i]: 1: 3,' ',yCi]: 1: 3);
i: =i+2; end;
e: =readkey; goto 1; end;
.' 3': begin
cirscr;
settextstyle(0,0,2) ;
outtextxy(150,280,'нажмите на любую клавишу ') ;
E: =readkey;
closegraph ;
end;
end;
close(ff);
end.
program diplom; <5 const n=200;
type mas=array[0. . n]of real;
var a,b,c,d,f,y,p,xx,1,r,g: mas;
x,h,jl,yl,j2,y2: real;
i: integer;
ff: text; „ о procedure vap(var
xx,y :mas); рвит^шло. Ьсир<лсцш^У<мо^ var x,h: real; i:
integer; f,p, a,b, c,d: mas; ^Cc^c^cc begin
h: =2/n; x: =0;
for i: =0 to n do begin
f[i]: = -1 ;
p[i]: = 0;
xx[i]: =x;
x: =x+h end;
y[0]:=0; y[157]:=l;
for i: =1 to 157 do
a[i]:=2+h*h*f[i];
b[l]:=y[0]-h*h*p[l];
b[156]: =y[157]-h*h*p[156];
for i: =2 to 157-2 do
b[i]: =-h*h*pCi];
c[l]:=a[l]; d[l]:=b[l];
for i: =2 to 157-1 do begin
c[i]: =a[i]-l/c[i-l];
d[i]: =b[i]+d[i-l]/c[i-l];
end;
y[156]: =d[156]/c[156];
for i: =2 to 156 do
y[157-i]: =(d[157-I] +y[157-i+l])/c[157-i];
end;
procedure kr(var xx,y :mas); р>влллели,<Л. ^сиг-С^Сл! ^wo^m.
var x,h: real;i: integer;a,p,g,f,r,1,b,c,d: mas; / </
begin
h: =2/n; x: =0;
for i: =0 to 100 do begin
P[i]:=0;
g[i]: =0;
fCi3: =x;
xx[i]: =x;
x: =x+h;
end;
У[0]: =0; y[100]: =1;
for i: =1 to 100 do begin
1[i]: =2-h*p[i];
a[i]: =(4-2*h*h*g[i])/l[i];
r[i]: =(2+h*p[i])/l[i];
end;
b[l]: =y[0]-2*h*h*f[l]/l[l];d[l]: =b[l];c[l]: =a[l];
for i: =2 to 99 do begin
- b[i]: =-2*h*h*f[i]/l[i];
c[i]: =a[i]-<r[i-l]/c[i-l]);
d[i]: =b[i]+(d[i-l]/c[i-l]);
end;
у[99]: =(d[99]+r[99]*y[100])/c[99];
for i: =2 to 99 do
yClOO-i]: =(d[100-i]+r[100-i]*y[100-i+l])/c[100-i];
end;
begin assign(ff,' b: res.dip');
rewrite(ff); writeln(ff); ^ vap(xx,y);
writeln(ff,' РЕШЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ');
writeln(ff);
i: =0;jl: =0;
writeln(ff,' численное решение',
','аналитическое решение');
writeln(ff);
while <i<=157) and (jl<=1.57) do begin
yl:=sin(jl);
writeln(ff,' ',xx[i]: 1: 2,' ',y[i]:l:3,
',J1:1: 2,' ' ,yl: 1: 3);
i: =i+l;jl: =jl+0. 01; end;
I writeln(ff,' ' ,xx[157]: 1: 2,' ' ,у[157]:1: 3, ',J1:1:
2,' ' ,yl: 1: 3);
writeln(ff);
kr(xx,y);
writeln(ff);
writeln(ff,' РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ' );
writeln(ff);i: =0;j2: =0;
writeln(ff,' численное решение',
' /аналитическое решение' );
writeln(ff);
while (i<=100) and (j2<=l) do begin
y2: =j2*j2*j2/6+(5>Kj2/6);
writeln(ff,' ',xx[i]:1: 2_,' ' ,y[i]:1: 3, ' ,j2: 1: 2,'
',у2: 1: 3);
i: =i+l;j2: =j2+0. 01; end;
writeln(ff,' ',хх[100]: 1: 2,' ',у[100]:1: 3, ' ,з2: 1:
2,' ' ,у2: 1: 3);
close(ff);
end.
Страницы: 1, 2
|
|
|
|
|
