|
|
|
|
Диплом: Когомологии де Рама
Диплом: Когомологии де Рама
Министерство образования Российской Федерации.
Саратовский Государственный Университет
имени Н.Г.Чернышевского.
кафедра геометрии.
Когомологии де Рама.
Дипломная работа
Студентки 5 курса механико-математического факультета, группы № 522,
****************************************************************
Научный руководитель:
*************
Зав. кафедрой:
*****************
Саратов, 2004
Оглавление.
Введение................................3
1. Цепи и интегрирование........................4
1.1 р-мерные симплексы и их свойства..............4
1.2 Дифференцируемые р-цепи на многообразии и их границы....7
1.3 Интегралы по р-мерным цепям................11
1.4 Теорема Стокса.....................13
2. Нульмерные и n-мерные когомологии...............15
2.1 Вычисление когомологий на компактном многообразии...16
2.2 Вычисление когомологий с компактным носителем.....19
Литература..........................24
Введение.
Теория гомологий и когомологий топологических пространств играет важную роль
в алгебраической топологии. Для дифференциальных многообразий имеется два
варианта теории гомологий и когомологий, а именно гомологии и когомологии с
произвольным носителем и компактным носителем. В качестве когомологий
многообразия берутся когомологии комплекса дифференциальных форм с
произвольными и компактными носителями, а в качестве гомологий берутся
гомологии комплекса конечных дифференциальных цепей и комплекса бесконечных
дифференциальных цепей. Кроме того, вычисляются нульмерные и n-мерные
когомологии обоих типов для n-мерных многообразий.
Данная дипломная работа состоит из двух разделов. Первый раздел состоит из
четырех пунктов, второй – из двух.
В пункте 1.1 рассматриваются определение р-мерного симплекса и его свойства.
В пункте 1.2 определяется сингулярный р-симплекс на дифференцируемом
многообразии, дифференцируемые р-цепи и бесконечные дифференцируемые р-цепи и
их границы. В пункте 1.3 рассматриваются р-мерные группы гомологий и
когомологий, для конечных и бесконечных цепей, а также – интеграл от р-формы
по р-цепям. В пункте 1.4 приводится теорема Стокса.
Раздел два посвящен вычислению когомологий. В пункте 2.1 вычисляются
когомологии на компактном многообразии, в пункте 2.2 – когомологии с
компактным носителем на многообразии.
Раздел 1. Цепи и интегрирование. 1.1 р-мерные симплексы и их свойства.
Определение: p-мерным симплексом 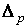 в р-мерном пространстве
в р-мерном пространстве 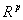 будем называть объект, определенный неравенствами
будем называть объект, определенный неравенствами 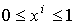 ,
, 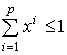 .
Рассмотрим примеры р-мерного симплекса.
р=1, тогда получаем .
Рассмотрим примеры р-мерного симплекса.
р=1, тогда получаем 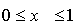 - то есть отрезок [0,1] - то есть отрезок [0,1]
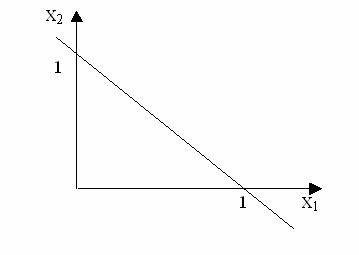
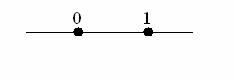 р=2, тогда
р=2, тогда 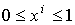 , ,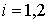 и x1+ x2=1, то есть, получаем треугольник и x1+ x2=1, то есть, получаем треугольник
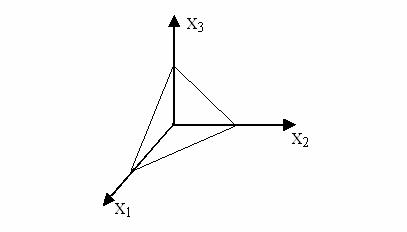
 р=3, тогда
р=3, тогда 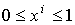 , ,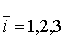 и x1+ x2 +x3=1, то есть, получаем тетраэдр. и x1+ x2 +x3=1, то есть, получаем тетраэдр.
 Для удобства введем в симплексе
Для удобства введем в симплексе 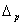 так называемые барицентрические координаты, которые определяются следующими
формулами
так называемые барицентрические координаты, которые определяются следующими
формулами
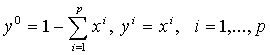 , тогда , тогда
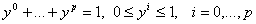 Определение. Отображение
Определение. Отображение 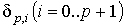 симплекса симплекса 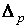 в в 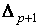 определяется формулой определяется формулой
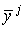 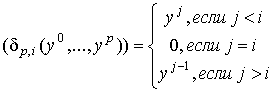 ,
где ,
где 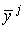 - барицентрические координаты в - барицентрические координаты в 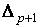 .
По определению .
По определению 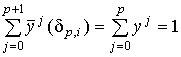 , то
формула (1.1) действительно определяет отображение , то
формула (1.1) действительно определяет отображение 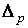 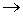 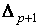 . Это отображение очевидным образом продолжается до дифференцируемого
отображения симплекса
. Это отображение очевидным образом продолжается до дифференцируемого
отображения симплекса 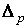 в пространстве
в пространстве 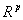 в
пространство в
пространство 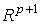 .
Рассмотрим образы симплекса .
Рассмотрим образы симплекса 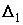 в симплексе в симплексе 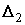 при данном отображении:
Симплекс при данном отображении:
Симплекс 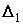 задается неравенствами задается неравенствами
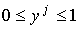 , ,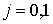 и y0+ y1=1.
Тогда при отображении и y0+ y1=1.
Тогда при отображении 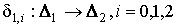 получаем следующее: получаем следующее:
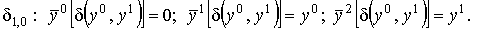
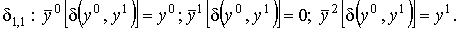
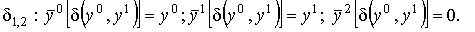 Таким образом, получаем следующее отображение
Таким образом, получаем следующее отображение
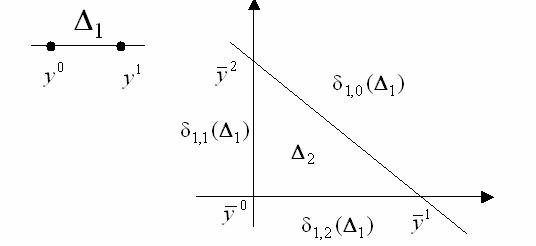 Сравним отображения
Сравним отображения 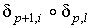 и
и 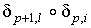 при условии при условии 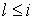 . Если
. Если 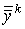 -
барицентрические координаты в -
барицентрические координаты в 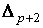 , то
, то
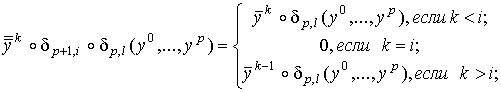 Так как
Так как 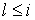 , то можно переписать это в виде: , то можно переписать это в виде: 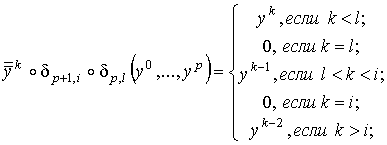 С другой стороны получаем
С другой стороны получаем
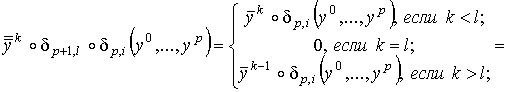
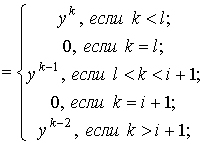 Отсюда получаем, что
Отсюда получаем, что 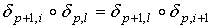 при условии при условии 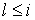
1.2 Дифференцируемые р-цепи на многообразии и их границы.
Пусть М – n-мерное многообразие класса 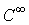 со счетной базой.
В дальнейшем будем считать дифференцируемое отображение – дифференцируемым
отображением класса со счетной базой.
В дальнейшем будем считать дифференцируемое отображение – дифференцируемым
отображением класса 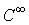 .
Определение. Дифференцируемым сингулярным р-симплексом на М
называется отображение
.
Определение. Дифференцируемым сингулярным р-симплексом на М
называется отображение 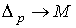 , которое может быть продолжено до дифференцируемого отображения некоторой
окрестности симплекса
, которое может быть продолжено до дифференцируемого отображения некоторой
окрестности симплекса 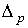 в
в 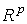 в многообразие М.
Дифференцируемой р-цепью называется конечная линейная комбинация
(с вещественными коэффициентами) сингулярных р-симплексов.
Бесконечной дифференцируемой р-цепью называется бесконечная сумма
сингулярных р-симплексов, то есть такое отображение в многообразие М.
Дифференцируемой р-цепью называется конечная линейная комбинация
(с вещественными коэффициентами) сингулярных р-симплексов.
Бесконечной дифференцируемой р-цепью называется бесконечная сумма
сингулярных р-симплексов, то есть такое отображение 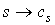 множества дифференцируемых сингулярных р-симплексов в вещественную прямую, что
множество
множества дифференцируемых сингулярных р-симплексов в вещественную прямую, что
множество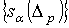 (где (где 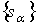 - множество тех s, для которых
- множество тех s, для которых 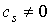 ) локально конечно. Другими словами, дифференцируемой р-цепью называется
комбинация
) локально конечно. Другими словами, дифференцируемой р-цепью называется
комбинация 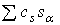 , где , где 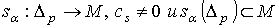 , причем
, причем 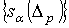 - локально
конечно, что значит - локально
конечно, что значит 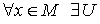 - окрестность x, такая, что U имеет непустое пересечение с
конечным числом
- окрестность x, такая, что U имеет непустое пересечение с
конечным числом 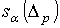 .
Лемма:1.1 На компактном многообразии бесконечная сингулярная
цепь является конечной.
Доказательство:
Пусть М – компактное пространство, то есть хаусдорфово пространство,
любое открытое покрытие которого содержит конечное подпокрытие. Тогда .
Лемма:1.1 На компактном многообразии бесконечная сингулярная
цепь является конечной.
Доказательство:
Пусть М – компактное пространство, то есть хаусдорфово пространство,
любое открытое покрытие которого содержит конечное подпокрытие. Тогда 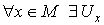 - окрестность x, такая, что
- окрестность x, такая, что 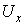 имеет непустое пересечение с конечным числом
имеет непустое пересечение с конечным числом 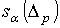 . Так как М – компактное, то существует конечное число окрестностей
. Так как М – компактное, то существует конечное число окрестностей 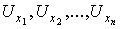 , которые покрывают все пространство М. Перебрав все окрестности, каждая из
которых имеет непустое пересечение с конечным числом
, которые покрывают все пространство М. Перебрав все окрестности, каждая из
которых имеет непустое пересечение с конечным числом 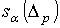 , получим , что на компактном многообразии бесконечная сингулярная цепь имеет не
более конечного числа ненулевых коэффициентов, то определение бесконечной
дифференцируемой р-цепи совпадает с определением дифференцируемой р-цепи.
Лемма доказана.
Множество всех р-цепей образует векторное пространство относительно сложения
цепей и умножения на скаляр. Определим эти операции. Суммой р-цепей будем
называть линейную комбинацию сингулярных р-симплексов, коэффициенты которой
получены из суммы коэффициентов при соответствующих р-симплексах (при
умножении на скаляр – соответствующие коэффициенты умножаются на скаляр).
Множество всех р-цепей будем обозначать
, получим , что на компактном многообразии бесконечная сингулярная цепь имеет не
более конечного числа ненулевых коэффициентов, то определение бесконечной
дифференцируемой р-цепи совпадает с определением дифференцируемой р-цепи.
Лемма доказана.
Множество всех р-цепей образует векторное пространство относительно сложения
цепей и умножения на скаляр. Определим эти операции. Суммой р-цепей будем
называть линейную комбинацию сингулярных р-симплексов, коэффициенты которой
получены из суммы коэффициентов при соответствующих р-симплексах (при
умножении на скаляр – соответствующие коэффициенты умножаются на скаляр).
Множество всех р-цепей будем обозначать 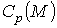 (множество бесконечных р-цепей
(множество бесконечных р-цепей 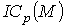 ). Если f – дифференцируемое отображение М1 в М
2 , то есть получаем
). Если f – дифференцируемое отображение М1 в М
2 , то есть получаем 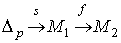 Полагая для симплексов
Полагая для симплексов 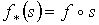 и продолжая отображение по линейности получим линейное отображение
и продолжая отображение по линейности получим линейное отображение 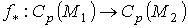 . Для бесконечных цепей на f накладываются дополнительные условия.
Отображение f называется собственным, если
. Для бесконечных цепей на f накладываются дополнительные условия.
Отображение f называется собственным, если 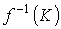 компактно для любого компактного
компактно для любого компактного 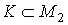 .
Пусть
.
Пусть 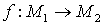 – собственное отображение и – собственное отображение и 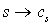 – цепь на – цепь на 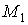 , то есть , то есть 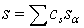 , где , где 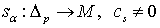 . Положим . Положим 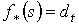 , где , где
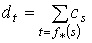 , (1.2)
причем , (1.2)
причем 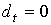 , если , если 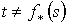 ни для какого s. Покажем, что сумма (1.2) конечна. Так как
ни для какого s. Покажем, что сумма (1.2) конечна. Так как 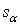 – симплекс на
– симплекс на 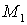 , то , то 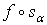 – сингулярный симплекс на
– сингулярный симплекс на 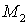 , тогда
, тогда 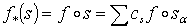 . Учитывая
возможность того, что . Учитывая
возможность того, что 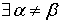 такие, что
такие, что 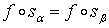 , и
приводя подобные члены, получаем, что сумма (1.2) конечна. Множество симплексов
t, для которых , и
приводя подобные члены, получаем, что сумма (1.2) конечна. Множество симплексов
t, для которых 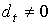 ,
локально конечно. Поэтому формула (1.2) определяет бесконечную р-цепь на ,
локально конечно. Поэтому формула (1.2) определяет бесконечную р-цепь на 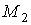 .
Пусть s – р-симплекс, тогда
.
Пусть s – р-симплекс, тогда 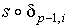 - (р-1) – симплекс. Определим границу симплекса s формулой
- (р-1) – симплекс. Определим границу симплекса s формулой 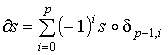 . То есть граница р- симплекса определяется (р-1)-симплексами, а знак указывает
направление обхода границы.
В качестве примера рассмотрим 2-симплекс:
. То есть граница р- симплекса определяется (р-1)-симплексами, а знак указывает
направление обхода границы.
В качестве примера рассмотрим 2-симплекс:
+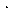 |
|
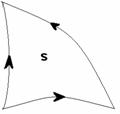 Продолжим
Продолжим 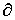 по
линейности до отображения по
линейности до отображения 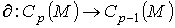 . Для бесконечных цепей отображение определяется аналогично:
. Для бесконечных цепей отображение определяется аналогично:
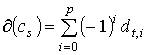 , , 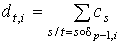 .
То есть для каждой р-цепи с (р-1)-цепь .
То есть для каждой р-цепи с (р-1)-цепь 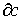 сопоставляет (р-1)-мерному сингулярному симплексу t число
сопоставляет (р-1)-мерному сингулярному симплексу t число 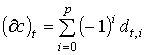 . Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение
. Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение 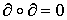 .
Из определения р-цепи следует, что равенство
.
Из определения р-цепи следует, что равенство 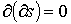 достаточно доказать для любого симплекса, тогда оно верно и для любой цепи.
Пусть s есть q-мерный симплекс. Если
достаточно доказать для любого симплекса, тогда оно верно и для любой цепи.
Пусть s есть q-мерный симплекс. Если 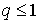 , то доказывать нечего. Если , то доказывать нечего. Если 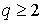 , то , то
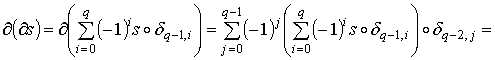
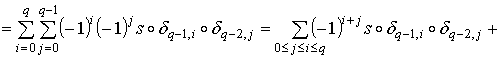
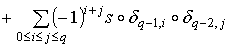 .
Так как .
Так как 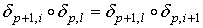 , то в нашем случае получим , то в нашем случае получим
 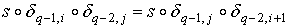 , если , если 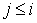 .
Тогда .
Тогда
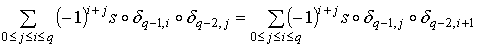
 положим
положим 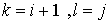
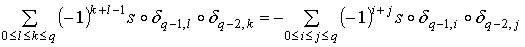 .
Таким образом, равенство
.
Таким образом, равенство 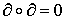 доказано. доказано.
1.3 Интегралы по р-мерным цепям.
Определение. р-цепь с, удовлетворяющая условию 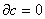 называется циклом; р-цепь вида
называется циклом; р-цепь вида 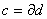 , где d – некоторая (р+1)-цепь называется границей.
Равенство
, где d – некоторая (р+1)-цепь называется границей.
Равенство 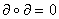 говорит о
том, что пространство границ есть подпространство пространства циклов.
Определение. Факторпространство пространства циклов по
пространству границ называется р-мерной группой гомологий и обозначается говорит о
том, что пространство границ есть подпространство пространства циклов.
Определение. Факторпространство пространства циклов по
пространству границ называется р-мерной группой гомологий и обозначается 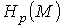 . Для бесконечных цепей р-мерная группа гомологий обозначается
. Для бесконечных цепей р-мерная группа гомологий обозначается 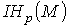 Из определения следует, что если
Из определения следует, что если 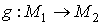 , то отображение
, то отображение 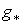 перестановочно с
перестановочно с 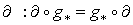 .
Поэтому .
Поэтому 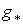 переводит
циклы в циклы, границы в границы.
Теперь рассмотрим дифференциальные формы и операцию внешнего дифференцирования
Определение. Носителем формы ω называется наименьшее
замкнутое множество, вне которого она равна нулю.
Определение. Дифференциальная р-форма ω называется
замкнутой, если переводит
циклы в циклы, границы в границы.
Теперь рассмотрим дифференциальные формы и операцию внешнего дифференцирования
Определение. Носителем формы ω называется наименьшее
замкнутое множество, вне которого она равна нулю.
Определение. Дифференциальная р-форма ω называется
замкнутой, если 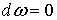 и
точной, если и
точной, если 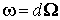 .
Замкнутые формы будем называть коциклами, точные – кограницами.
Из равенства .
Замкнутые формы будем называть коциклами, точные – кограницами.
Из равенства 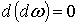 следует, что пространство кограниц есть подпространство пространства коциклов.
Определение. Факторпространство замкнутых р-форм по точным
р-формам называется р-мерной группой когомологий (де Рама) многообразия М и
обозначается
следует, что пространство кограниц есть подпространство пространства коциклов.
Определение. Факторпространство замкнутых р-форм по точным
р-формам называется р-мерной группой когомологий (де Рама) многообразия М и
обозначается 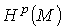 Определение. Факторпространство замкнутых р-форм с компактным
носителем по точным р-формам с компактным носителем называется р-мерной группой
когомологий с компактным носителем многообразия М и обозначается
Определение. Факторпространство замкнутых р-форм с компактным
носителем по точным р-формам с компактным носителем называется р-мерной группой
когомологий с компактным носителем многообразия М и обозначается 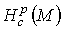 Заметим, что для компактного многообразия носитель формы всегда является
компактным множеством. Тогда группа когомологий совпадает с группой
когомологий с компактным носителем.
Определим интеграл от р-формы по р-цепи:
Определение. Пусть s – сингулярный р-симплекс, а
Заметим, что для компактного многообразия носитель формы всегда является
компактным множеством. Тогда группа когомологий совпадает с группой
когомологий с компактным носителем.
Определим интеграл от р-формы по р-цепи:
Определение. Пусть s – сингулярный р-симплекс, а 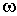 – дифференциальная форма степени р. Форма
– дифференциальная форма степени р. Форма 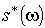 определена в некоторой окрестности евклидова р-симплекса
определена в некоторой окрестности евклидова р-симплекса 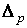 . Допустим, что,
. Допустим, что, 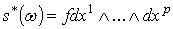 где
где 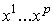 - стандартные
координаты в - стандартные
координаты в 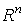 .
Положим по определению, .
Положим по определению, 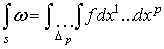 (1.3)
Продолжим (1.3) на любую конечную р-цепь по линейности. В общем случае нельзя
интегрировать произвольную р-форму по бесконечной р-цепи, так как это может
привести к расходящемуся бесконечному ряду.
Если ω – форма с компактным носителем, то для любой бесконечной цепи
(1.3)
Продолжим (1.3) на любую конечную р-цепь по линейности. В общем случае нельзя
интегрировать произвольную р-форму по бесконечной р-цепи, так как это может
привести к расходящемуся бесконечному ряду.
Если ω – форма с компактным носителем, то для любой бесконечной цепи 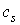 сумма
сумма  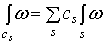 имеет только конечное число ненулевых членов и поэтому определена.
Пусть
имеет только конечное число ненулевых членов и поэтому определена.
Пусть 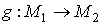 -
собственное дифференцируемое отображение. Из определения следует, что -
собственное дифференцируемое отображение. Из определения следует, что 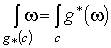 , так как
, так как 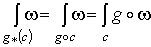 и и 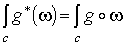 .
.
1.4 Теорема Стокса.
Теорема Стокса. Для любой р-цепи с и (р-1)-формы 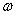 (соответственно бесконечной р-цепи с и (р-1)-формы с компактным носителем)
справедливо равенство
(соответственно бесконечной р-цепи с и (р-1)-формы с компактным носителем)
справедливо равенство 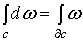 Доказательство.
Благодаря линейности по с обеих частей формулы
Доказательство.
Благодаря линейности по с обеих частей формулы 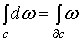 достаточно рассмотреть случай
достаточно рассмотреть случай 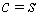 , где
, где 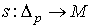 - сингулярный
р-симплекс. В этом случае наша формула сводится к равенству - сингулярный
р-симплекс. В этом случае наша формула сводится к равенству
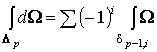 , (1.4)
где , (1.4)
где 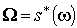 , а , а 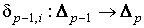 рассматривается как сингулярный (р-1)-симплекс в
рассматривается как сингулярный (р-1)-симплекс в 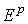 . По определению . По определению
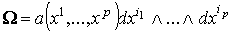 .
Достаточно доказать формулу (1.4) для каждого члена этой суммы. Таким
образом, задача сводится к проверке равенства .
Достаточно доказать формулу (1.4) для каждого члена этой суммы. Таким
образом, задача сводится к проверке равенства
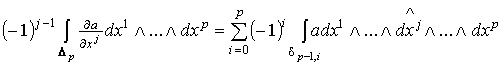 . (1.5)
Так как
. (1.5)
Так как 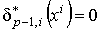 , то в
правой части останутся только члены с , то в
правой части останутся только члены с 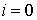 и
и 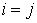 . Пусть . Пусть 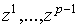 – евклидовы координаты в
– евклидовы координаты в 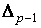 . Тогда
. Тогда
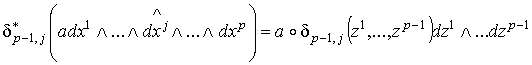 и
и 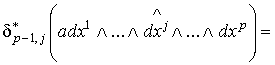
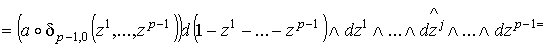
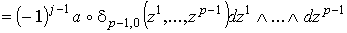 .
В соответствии с определениями (1.5) сводится к равенству .
В соответствии с определениями (1.5) сводится к равенству
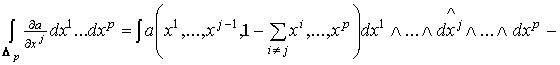
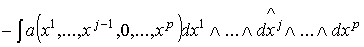 .
Из равенства .
Из равенства 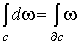 следует, что интегралы точной формы по циклу и замкнутой формы по границе равны
нулю. Таким образом, справедливы следующие следствия:
Следствие 1. Билинейное отображение
следует, что интегралы точной формы по циклу и замкнутой формы по границе равны
нулю. Таким образом, справедливы следующие следствия:
Следствие 1. Билинейное отображение 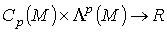 ,определяемое интегралом
,определяемое интегралом 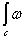 , индуцирует билинейное отображение
, индуцирует билинейное отображение 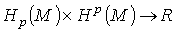 .
То есть отображение
.
То есть отображение 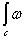 является билинейным и не зависит от выбора представителя.
Рассмотрим замкнутую р-форму ω и р-цикл с, такие что является билинейным и не зависит от выбора представителя.
Рассмотрим замкнутую р-форму ω и р-цикл с, такие что 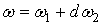 и и 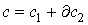 . Тогда . Тогда
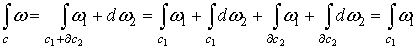 .
Аналогично следствию 1 получаем:
Следствие 2. Билинейное отображение
.
Аналогично следствию 1 получаем:
Следствие 2. Билинейное отображение 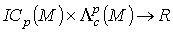 ,определяемое интегралом
,определяемое интегралом 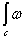 , индуцирует билинейное отображение
, индуцирует билинейное отображение 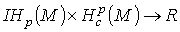 .
.
Раздел 2. Нульмерные и n-мерные когомологии.
Согласно определению, не существует нульмерных кограниц. Поэтому нульмерная
группа когомологий совпадает с группой коциклов. Но 0-форма есть просто
функция, а 0-коцикл есть такая функция f, что 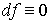 , то есть локально постоянная функция. Таким образом,
, то есть локально постоянная функция. Таким образом, 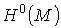 является пространством всех локально постоянных вещественных функций на М
. Поскольку любая локально постоянная функция постоянна на связных компонентах
многообразия М, то
является пространством всех локально постоянных вещественных функций на М
. Поскольку любая локально постоянная функция постоянна на связных компонентах
многообразия М, то 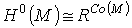 , где Со(М) есть множество компонент в М. В частности, если
М связно, то
, где Со(М) есть множество компонент в М. В частности, если
М связно, то 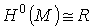 .
Функция f является компактным коциклом, если она локально постоянна и
supp f компактен. Это означает, что .
Функция f является компактным коциклом, если она локально постоянна и
supp f компактен. Это означает, что 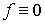 на некомпактных компонентах многообразия М. Поэтому
на некомпактных компонентах многообразия М. Поэтому 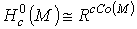 , где
, где 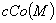 есть
множество компактных компонент многообразия М. В частности, если М
связно, то есть
множество компактных компонент многообразия М. В частности, если М
связно, то 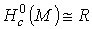 для
компактного многообразия М и для
компактного многообразия М и 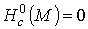 для некомпактного М.
для некомпактного М.
2.1 Вычисление когомологий на компактном многообразии.
Рассмотрим в 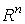 шар шар 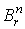 радиуса r. Тогда можно вычислить
радиуса r. Тогда можно вычислить 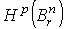 для всех р. Именно, справедлива
Теорема 2.1 (лемма Пуанкаре). Пусть w - форма степени
для всех р. Именно, справедлива
Теорема 2.1 (лемма Пуанкаре). Пусть w - форма степени 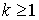 , определенная на
, определенная на 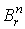 ,
и пусть ,
и пусть 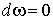 . Тогда
существует такая форма W, определенная на . Тогда
существует такая форма W, определенная на 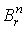 , что
, что 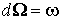 .
Докажем теорему индукцией по размерности n. Для .
Докажем теорему индукцией по размерности n. Для 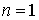 можно считать
можно считать 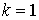 ; все
другие случаи тривиальны. Если ; все
другие случаи тривиальны. Если 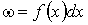 , то достаточно положить
, то достаточно положить 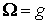 , где
, где 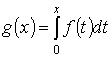 .
Сделаем следующее замечание:
Лемма 2.1. Если .
Сделаем следующее замечание:
Лемма 2.1. Если 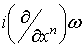 =0 и =0 и 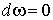 , то , то 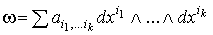 , где , где 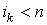 и и 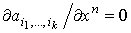 .
Действительно, .
Действительно,
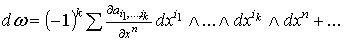 ,
где остальные члены не содержат ,
где остальные члены не содержат 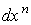 .
Перейдем к доказательству теоремы.
Пусть .
Перейдем к доказательству теоремы.
Пусть 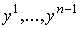 – декартовы координаты в – декартовы координаты в 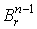 , и пусть , и пусть 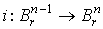 - отображение, задаваемое формулами - отображение, задаваемое формулами
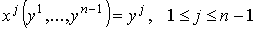 , ,
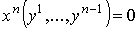 ,
где ,
где 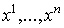 - декартовы
координаты в - декартовы
координаты в 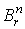 .
Тогда .
Тогда 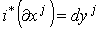 для для 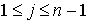 и
и 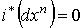 . Пусть р
– отображение шара . Пусть р
– отображение шара 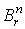 на
на 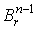 , определяемое
формулой , определяемое
формулой
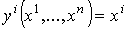 для для 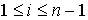 .
Имеем .
Имеем 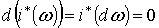 . По
предположению индукции . По
предположению индукции 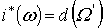 для некоторой формы
для некоторой формы 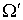 на
на 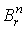 . Положим . Положим 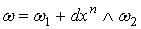 . Где
. Где 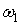 и и 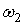 - формы от
- формы от  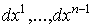 . Определим форму W следующими условиями:
1.
. Определим форму W следующими условиями:
1. 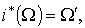 2.
2. 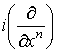 W=0,
3. W=0,
3. 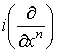 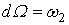 В терминах координат
В терминах координат 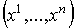 условие 2. означает, что форма W может быть записана в виде
условие 2. означает, что форма W может быть записана в виде
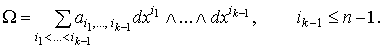 Условие 1. означает, что
Условие 1. означает, что 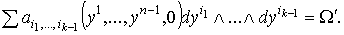 Условие 2. означает, что
Условие 2. означает, что 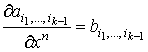 , если , если 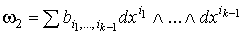 .
Отсюда видно, что существует единственная форма W, удовлетворяющая условиям
1,2,3, которая может быть найдена с помощью интегрирования по .
Отсюда видно, что существует единственная форма W, удовлетворяющая условиям
1,2,3, которая может быть найдена с помощью интегрирования по 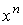 . Мы утверждаем, что
. Мы утверждаем, что 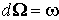 . Действительно,
. Действительно,
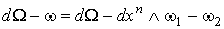 .
Но .
Но 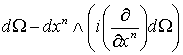 есть дифференциальная форма, не содержащая есть дифференциальная форма, не содержащая 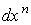 . Поэтому . Поэтому
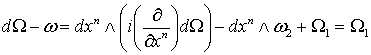 ,
где ,
где 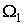 не зависит от не зависит от 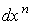 . Поскольку . Поскольку 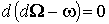 , мы можем применить лемму 2.1. Таким образом, , мы можем применить лемму 2.1. Таким образом,
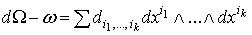 , где , где 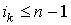 и и 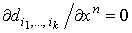 .
С другой стороны, .
С другой стороны,
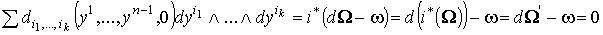 . Значит,
. Значит, 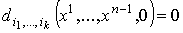 и и 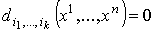 . Другими словами, . Другими словами, 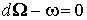 , что и доказывает теорему 2.1.
Следствие 2.1. , что и доказывает теорему 2.1.
Следствие 2.1. 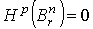 для для 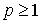 .
В доказательстве теоремы 2.1. коэффициенты формы W из коэффициентов формы w
интегрированием. Поэтому, если коэффициенты формы w дифференцируемо зависят
от некоторых дополнительных параметров, то форма W также дифференцируемо
зависит от этих параметров.
Следствие 2.2. Если в теореме 2.1. форма w дифференцируемо зависит от
параметров, то есть .
В доказательстве теоремы 2.1. коэффициенты формы W из коэффициентов формы w
интегрированием. Поэтому, если коэффициенты формы w дифференцируемо зависят
от некоторых дополнительных параметров, то форма W также дифференцируемо
зависит от этих параметров.
Следствие 2.2. Если в теореме 2.1. форма w дифференцируемо зависит от
параметров, то есть 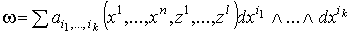 , где
, где 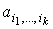 –
дифференцируемые функции от –
дифференцируемые функции от 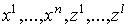 и
и 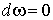 (оператор d
берется по (оператор d
берется по 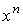 ), то ), то 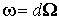 , где
, где 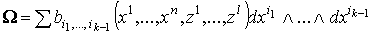 , причем , причем 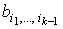 - дифференцируемые функции всех n+l переменных.
- дифференцируемые функции всех n+l переменных.
2.2 Вычисление когомологий с компактным носителем.
Мы хотим вычислить 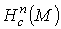 для любого многообразия М.
Лемма 2.2. Пусть w - такая n-форма, определенная на для любого многообразия М.
Лемма 2.2. Пусть w - такая n-форма, определенная на 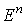 , что
1. supp , что
1. supp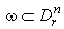 , где , где 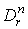 - куб - куб 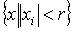 2.
2. 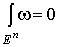 .
Тогда мы можем найти такую (n-1)-форму W, что
3. supp .
Тогда мы можем найти такую (n-1)-форму W, что
3. supp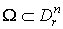 ,
4. ,
4. 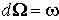 .
Доказательство:
Доказательство проведем с помощью индукции. Для любой k-формы p,
выраженной через .
Доказательство:
Доказательство проведем с помощью индукции. Для любой k-формы p,
выраженной через 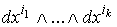 ,
обозначим символом ,
обозначим символом 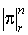 максимум абсолютных значений ее коэффициентов в
максимум абсолютных значений ее коэффициентов в 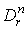 . Мы будем говорить, что семейство форм
. Мы будем говорить, что семейство форм 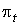 дифференцируемо зависит от t, если каждый коэффициент есть
дифференцируемая функция от
дифференцируемо зависит от t, если каждый коэффициент есть
дифференцируемая функция от 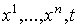 . Здесь t обозначает s-мерный параметр,
. Здесь t обозначает s-мерный параметр, 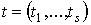 . Наше индуктивное предположение состоит в следующем:
Пусть
. Наше индуктивное предположение состоит в следующем:
Пусть 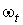 -
семейство форм на -
семейство форм на 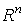 ,
дифференцируемо зависящее от t. Предположим, что для каждого значения t форма ,
дифференцируемо зависящее от t. Предположим, что для каждого значения t форма 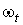 удовлетворяет условиям 1. и 2. Тогда существует такое дифференцируемое семейство
форм
удовлетворяет условиям 1. и 2. Тогда существует такое дифференцируемое семейство
форм 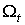 ,
удовлетворяющее условию 3., что ,
удовлетворяющее условию 3., что 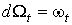 и
5.
и
5. 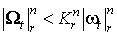 ,
где ,
где 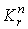 зависит только от n и r
Для зависит только от n и r
Для 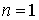 мы можем
написать мы можем
написать 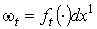 .
Определим функцию .
Определим функцию 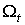 равенством
равенством 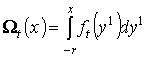 .Очевидно, что
.Очевидно, что 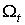 есть
дифференцируемое семейство 0-форм, удовлетворяющих условиям 3., 4. и 5.
Допустим, что предположение индукции выполнено для n-1. Пусть есть
дифференцируемое семейство 0-форм, удовлетворяющих условиям 3., 4. и 5.
Допустим, что предположение индукции выполнено для n-1. Пусть
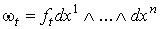 .
И пусть .
И пусть 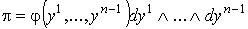 есть
положительная форма на есть
положительная форма на 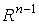 , такая, что supp
, такая, что supp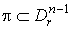 и
и 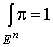 . Рассмотрим формы . Рассмотрим формы 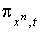 на
на 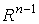 (зависящие от
параметров (зависящие от
параметров 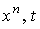 ),
определяемые формулой ),
определяемые формулой
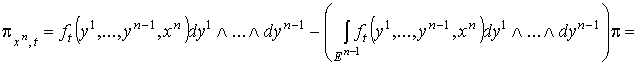
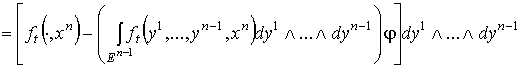 . (2.1)
Они образуют дифференцируемое семейство
. (2.1)
Они образуют дифференцируемое семейство 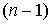 -форм, удовлетворяющее предположению индукции. Кроме того,
-форм, удовлетворяющее предположению индукции. Кроме того, 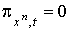 , если
, если 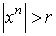 . Поэтому мы
можем написать . Поэтому мы
можем написать
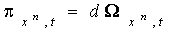 (2.2)
Пусть (2.2)
Пусть 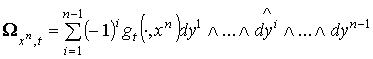 , где , где 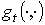 – дифференцируемые функции на – дифференцируемые функции на 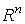 . Определим форму . Определим форму 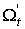 равенством равенством
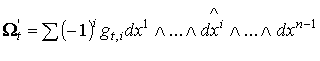 ,
так что ,
так что 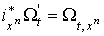 , где , где 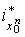 есть вложение есть вложение 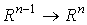 , заданное формулами , заданное формулами
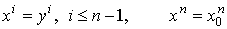 .
При вычислении формы .
При вычислении формы 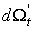 встретятся два типа членов: содержащие частные производные по
встретятся два типа членов: содержащие частные производные по 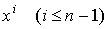 содержащие частную производную по
содержащие частную производную по 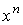 . Умножением на
. Умножением на 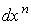 мы
избавимся от членов, содержащих мы
избавимся от членов, содержащих 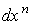 , и, значит для каждого значения
, и, значит для каждого значения 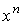 будем иметь
будем иметь 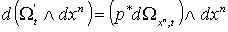 , где
р есть проекция , где
р есть проекция 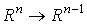 вдоль
вдоль 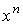 . Положим . Положим 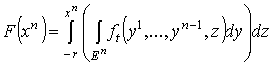 . Тогда
. Тогда 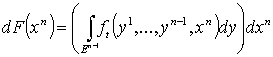 . Положим . Положим
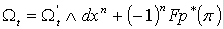 . (2.3)
Имеем . (2.3)
Имеем 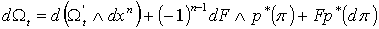 . Но . Но 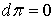 , поскольку p есть (n-1)-форма на , поскольку p есть (n-1)-форма на 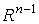 . Поэтому . Поэтому
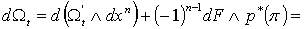
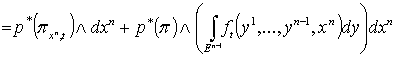 . (2.4)
Далее, формы . (2.4)
Далее, формы  p и p и 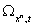 , а значит, и форма
, а значит, и форма 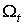 обращаются в нуль при
обращаются в нуль при 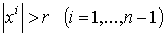 . Если
. Если 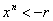 или или 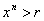 , то последний интеграл также обращается в нуль, поскольку
, то последний интеграл также обращается в нуль, поскольку
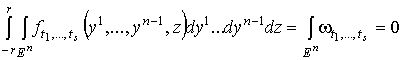 .
Форма
.
Форма 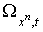 обращается в нуль, если обращается в нуль, если 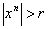 , так как по индуктивному предположению 5. , так как по индуктивному предположению 5.
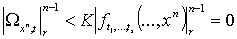 при при 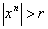 .
Наконец, формы встречающиеся в правой части формулы (2.3), очевидно образуют
дифференцируемое семейство форм и удовлетворяют оценке 5., где .
Наконец, формы встречающиеся в правой части формулы (2.3), очевидно образуют
дифференцируемое семейство форм и удовлетворяют оценке 5., где 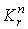 зависят от
зависят от 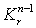 и
от выбора j. Лемма доказана.
С помощью леммы 2.2. доказывается
Лемма 2.3. Если М – связное n-мерное многообразие, то и
от выбора j. Лемма доказана.
С помощью леммы 2.2. доказывается
Лемма 2.3. Если М – связное n-мерное многообразие, то 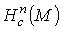 есть либо R, либо {0} (то есть
есть либо R, либо {0} (то есть 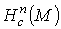 не более чем одномерно).
Пусть
не более чем одномерно).
Пусть 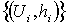 - такой атлас
на М, что каждая окрестность - такой атлас
на М, что каждая окрестность 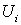 имеет вид
имеет вид 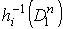 . Пусть W
- такая n-форма, что supp . Пусть W
- такая n-форма, что supp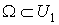 и
и 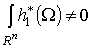 . Лемма будет
доказана, если для любой n-формы w с компактным носителем мы найдем
такое вещественное число с, что . Лемма будет
доказана, если для любой n-формы w с компактным носителем мы найдем
такое вещественное число с, что
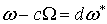 , (2.5)
где , (2.5)
где 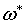 есть (n-1)
-форма с компактным носителем. Пусть есть (n-1)
-форма с компактным носителем. Пусть 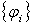 - разбиение единицы, подчиненное покрытию
- разбиение единицы, подчиненное покрытию 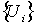 . Тогда
. Тогда 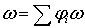 - конечная
сумма, и достаточно провести доказательство для каждого слагаемого в
отдельности. Поэтому можно считать, что supp - конечная
сумма, и достаточно провести доказательство для каждого слагаемого в
отдельности. Поэтому можно считать, что supp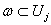 для некоторого j. Пусть р – точка из
для некоторого j. Пусть р – точка из 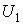 , а q – из
, а q – из 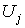 .
Пусть .
Пусть 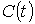 – такая
кривая, что – такая
кривая, что 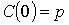 и и 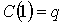 . Покроем
. Покроем 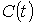 конечным
числом окрестностей конечным
числом окрестностей 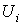 . Изменив, если потребуется, их нумерацию, мы можем считать, что это окрестности
. Изменив, если потребуется, их нумерацию, мы можем считать, что это окрестности 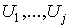 , причем
, причем 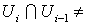 Æ
Пусть Æ
Пусть 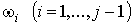 – такие
формы, что
supp – такие
формы, что
supp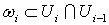 , , 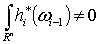 .
Положим .
Положим 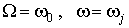 .
Рассмотрим формы .
Рассмотрим формы 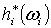 и и 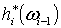 на
на 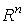 с носителями в с носителями в 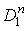 . Поскольку
. Поскольку 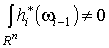 ,
существуют константы ,
существуют константы
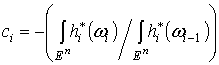 такие, что
такие, что 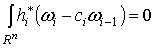 . По лемме 2.2. . По лемме 2.2.
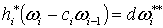 , (2.6)
причем supp , (2.6)
причем supp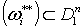 .
Форма .
Форма 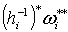 определена в определена в 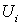 и имеет носитель в
и имеет носитель в 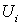 .
Определим на М форму .
Определим на М форму 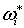 , полагая
, полагая 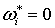 вне вне 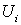 и
и 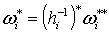 на на 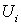 . Тогда равенство (2.6) можно переписать в виде
. Тогда равенство (2.6) можно переписать в виде
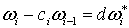 . (2.7)
Складывая с подходящими весами равенства (2.7) при . (2.7)
Складывая с подходящими весами равенства (2.7) при 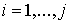 , мы получим равенство (2.5) , где
, мы получим равенство (2.5) , где
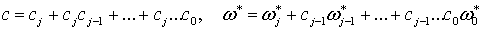 .
.
Литература.
1. Александров П.С. "Введение в теорию множеств и общую
топологию", Москва
2. Александров П.С., Пасынков Б.С. "Введение в теорию
размерности", Москва
3. Бураго Ю.Д., Залгаллер В.А. "Риманова геометрия", Санкт-
Петербург, Наука, 1994
4. Дубровин Б.А., Новиков С.П., Фоменко А.Т. "Современная
геометрия", Москва
5. Келли Дж. "Общая топология", Москва
6. Колмогоров А.Н., Фомин В.С "Элементы теории функций и
функционального анализа", Москва
7. Погорелов А.В. "Дифференциальная геометрия", Москва, Наука, 1969
8. Понтрягин Л.С. "Гладкие многообразия и их применение в теории
гомотопий", Москва, Наука, 1984
9. Постников М.М. "Группы Ли", Москва
10. Стернберг
11. Фоменко А.Т., Фукс Д.Б. "Курс гомотопической топологии", Москва,
Наука, 1989
|
|
|
|
|

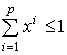 .
Рассмотрим примеры р-мерного симплекса.
р=1, тогда получаем
.
Рассмотрим примеры р-мерного симплекса.
р=1, тогда получаем 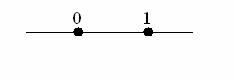 р=2, тогда
р=2, тогда  р=3, тогда
р=3, тогда  Для удобства введем в симплексе
Для удобства введем в симплексе 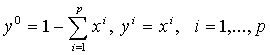 , тогда
, тогда
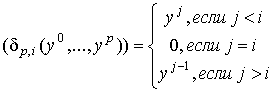 ,
где
,
где 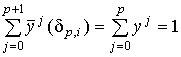 , то
формула (1.1) действительно определяет отображение
, то
формула (1.1) действительно определяет отображение  Сравним отображения
Сравним отображения 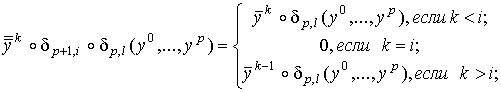 Так как
Так как 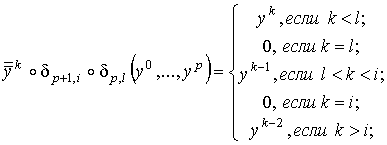 С другой стороны получаем
С другой стороны получаем
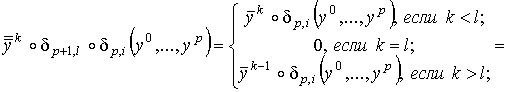
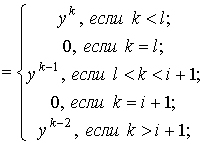 Отсюда получаем, что
Отсюда получаем, что 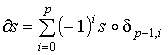 . То есть граница р- симплекса определяется (р-1)-симплексами, а знак указывает
направление обхода границы.
В качестве примера рассмотрим 2-симплекс:
. То есть граница р- симплекса определяется (р-1)-симплексами, а знак указывает
направление обхода границы.
В качестве примера рассмотрим 2-симплекс:
 Продолжим
Продолжим 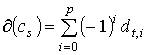 ,
, 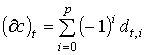 . Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение
. Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение 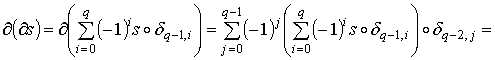
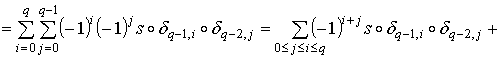
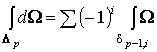 , (1.4)
где
, (1.4)
где 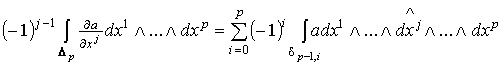 . (1.5)
Так как
. (1.5)
Так как 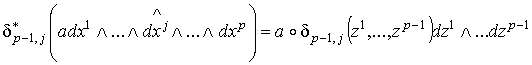 и
и 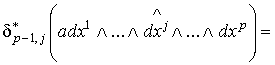
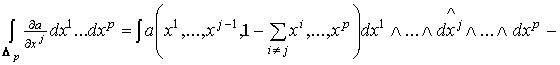
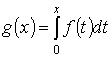 .
Сделаем следующее замечание:
Лемма 2.1. Если
.
Сделаем следующее замечание:
Лемма 2.1. Если 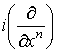 W=0,
3.
W=0,
3. 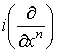
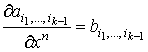 , если
, если 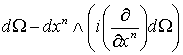 есть дифференциальная форма, не содержащая
есть дифференциальная форма, не содержащая 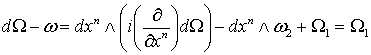 ,
где
,
где 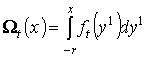 .Очевидно, что
.Очевидно, что 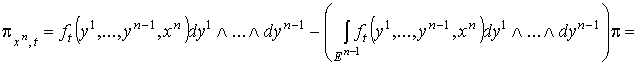
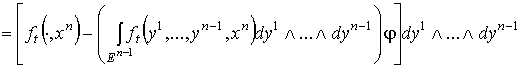 . (2.1)
Они образуют дифференцируемое семейство
. (2.1)
Они образуют дифференцируемое семейство 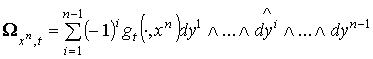 , где
, где 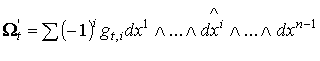 ,
так что
,
так что 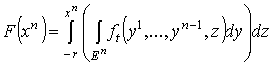 . Тогда
. Тогда 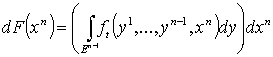 . Положим
. Положим
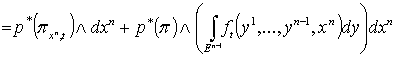 . (2.4)
Далее, формы
. (2.4)
Далее, формы 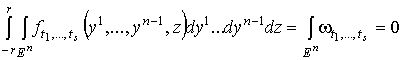 .
Форма
.
Форма 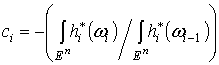 такие, что
такие, что 