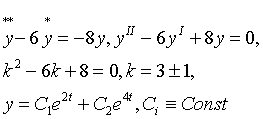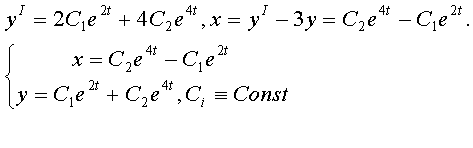 |
РУБРИКИ |
Контрольная: Дифференциальные уравнения |
РЕКОМЕНДУЕМ |
||
|
Контрольная: Дифференциальные уравненияКонтрольная: Дифференциальные уравненияВариант № 12 « Дифференциальные уравнения» Найти общий интеграл диф. ур-я
разделив обе части уравнения на x и сделав преобразования получим:
Используем подстановку Окончательно, получим (учитывая, что t=y/x)
Выполним перенос системы координат , решив Ур-е в «новой» системе координат: ,где Учитывая, что Получим диф. Ур-е вида Подстановка Дает решение вида
Выполнив преобразования
Т. к. p=q , то это Ур-е в полных дифференциалах Пользуясь общим правилом нахождения полного дифференциала, получим Откуда
Найти решение задачи Коши: · 5) Решение Ур-я такого типа следует искать в виде:
Подстановка в исходное Ур-е даст: Возмем интеграл по частям Konst найдем из начального условия, т.е. Решение
Помня, что Подстановка в исходное Ур-е дает Общее Решение: 7) Найти общее решение д.у.
9)
Решим однородное Ур-е (правая часть =0) Используя метод «Вариации постоянных» получим
Таким образом, решение данного д.ур-я имеет вид: Откуда,
Решение: Пусть X(t)=ASin(wt) –ур-е движения М. Т. , где t-время, А=А(t)- амплитуда колебаний. Тогда F1=kX, где к-некоторый коэффициент пропорциональности; Сила F2 , согласно условию, уравновешивает силу F1, т. е. F1=F2. Где F2=kV,V- скорость М.Т. (V=dX/dt) Откуда, Ч/З период времени Т амплитуда изменится
Найти общее решение д.у.
Решаем изначально однородное Ур-е (т.е. без правой части), соответствующее ему характеристическое ур-е: Первый корень без труда может быть подобран, Далее, разделив многочлен на Поскольку тут один корень (-1) имеет кратность, равную 2, то решение однородного Ур-я имеет вид: Общее решение д.у. где частное решение д. у. ищем в соответствии с правой частью уравнения, а именно: Подстановка в уравнение дает: Решение:
Указать вид частного решения для д.у. с постоянными коэффициентами 3-го порядка для различных правых частей и корней характеристического ур-я ( 1/7; -1/7+2i; -1/7-2i)
Пусть F(x) вид частного решения, соответствующей правой части f(x) Где Частное решение будет складывается из двух составляющих 1) частного решения, соответствующего паре комплексно сопряженных корней характеристического Ур-я и 2) частного решения, соответствующего многочлену 3-ей степени, т.е. Где Р(х)- многочлен 3-ей степени. Решить систему д.у.:
Из Ур-я (1) вычтем 3 ур-я (2),а затем из Ур-я (2) выразим dx/dt и подставим в (1). Вот, что будет: Где точки (*) обозначают дифференцирование по t. Типовые и курсовые по Высшей математике, консультации. Запись CD (аудио КД, МР-3,фильмы MPEG-4,Софт-коллекции) Недорого (3512)95-26-32 c 21 до 24 |
|
это ур-е с разделяющимеся переменными
, тогда
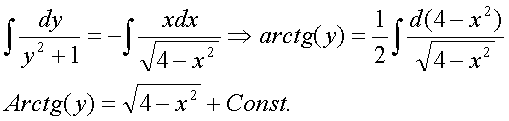
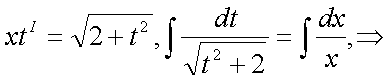
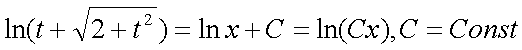
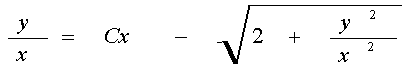
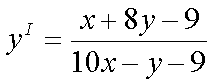
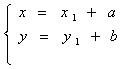
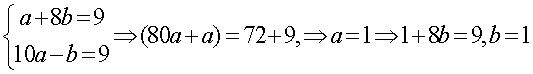
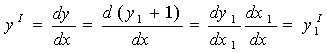
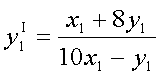
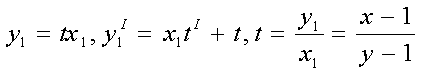
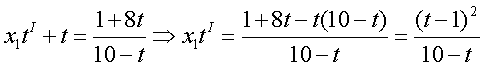
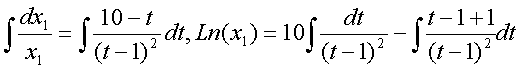
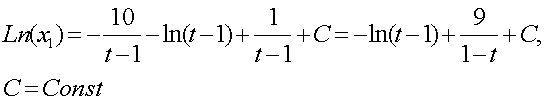
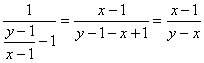получим, окончательно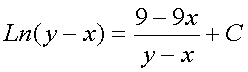
,
,
.
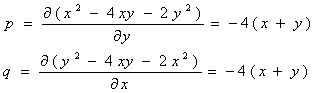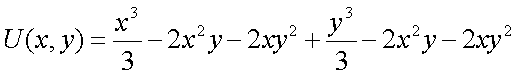
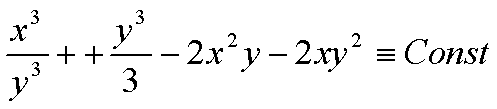
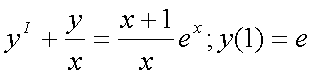
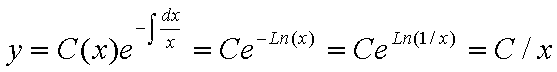
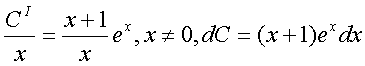
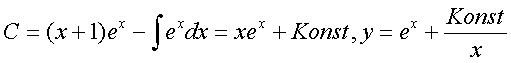
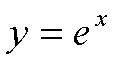
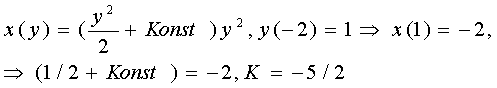
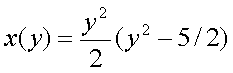
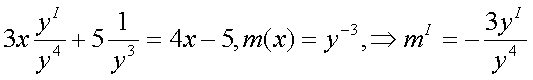
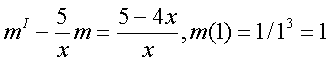
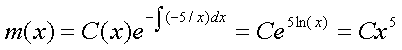
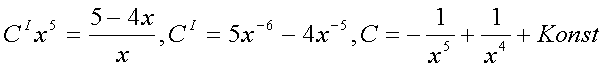
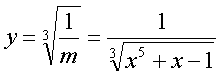
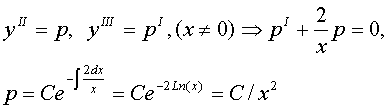
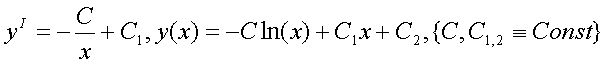
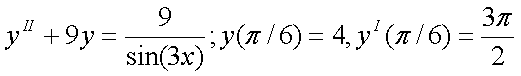
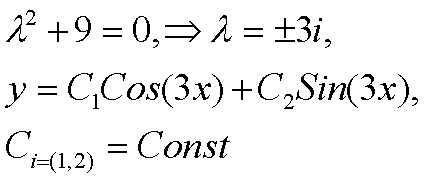
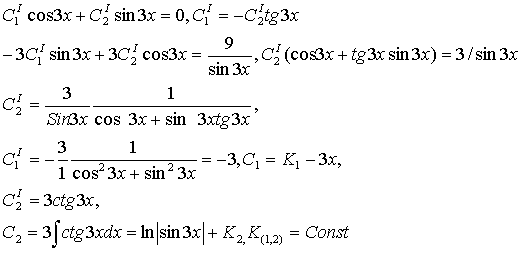
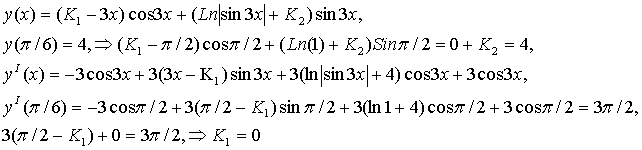
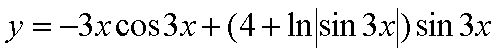
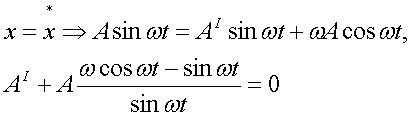
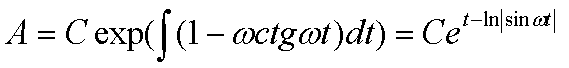
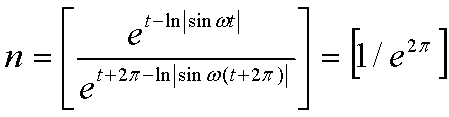
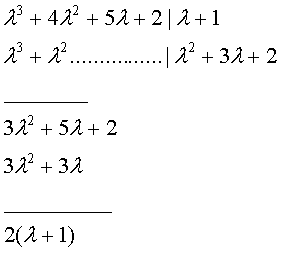
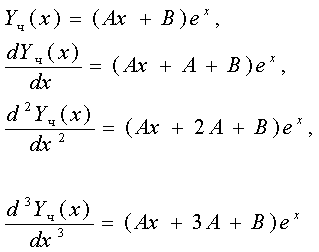
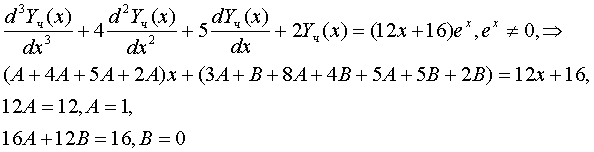
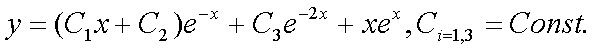
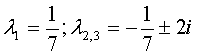
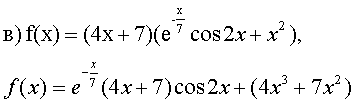
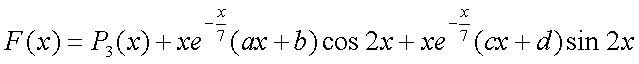
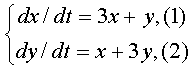
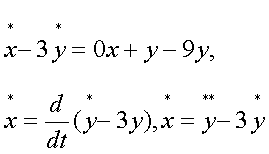получим:
многочлены 3-ей степени, т. е. такого вида
,
© 2010 |
|