|
|
|
|
Контрольная: Классические задачи теории вероятностей
Контрольная: Классические задачи теории вероятностей
ЗАДАЧА № 3 В связке 5 разных ключей, и один из них соответствующей
двери. Делается попытка открыть наудачу взятым колючем, ключ неподходящий более
не используется. Найти вероятность того, что
А) дверь будет открыта 1-ым ключем; Б) Для открытия двери будет использовано
не более двух ключей.
Решение:
Используем классическое определение вероятности.
P=m/n , где m – благоприятное число исходов, n- возможное число исходов.
Тогда
P(A)=1/5
Вероятность второго случая складывается из вероятностей двух событий,
соответствующих случаю А) и случаю, при котором второй ключ будет подобран
правильно (ТЕОРЕМА СЛОЖЕНИЯ СОБЫТИЙ) . Вероятность такого случая
P2=(4/5)(1/4)=1/5
В конечном случае, P(Б)=P(A)+P2=2/5
ЗАДАЧА № 4 Вероятность выигрыша по лотерейному билету p=1/7. Какова
вероятность того, что обладатель 5 билетов выиграет:
А) по всем 5;
Б) ни по одному;
В) хотя Бы по одному билету?
Решение:
Используем формулу Бернулли : 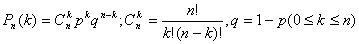 В нашем случае p=1/7; q=1-p=6/7;n=5
Тогда
А)
В нашем случае p=1/7; q=1-p=6/7;n=5
Тогда
А) 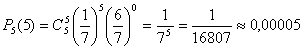 т. е. это практически невозможное событие
Б) т. е. это практически невозможное событие
Б) 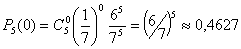 В) Хотя бы один : P=P(0)+P(1), где
В) Хотя бы один : P=P(0)+P(1), где 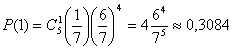 P=0,4627+0,3084=0,7711
ЗАДАЧА № 5 При приёме партии изделий проверяется половина, условие
приёмки – наличие брака менее 2 %. Какова вероятность того, что партия из 100
изделий, содержащая 5% брака, будет принята?
Решение:
Используем формулу Бернулли , в которой положим p= 0,05 ; q=1-0,05=0,95
Проверяем партию из 100/2 =50 изделий, в которой для приема быть не
должно более 50*2%=50*(1/50)=1 бракованной детали, тогда искомая
вероятность
P=0,4627+0,3084=0,7711
ЗАДАЧА № 5 При приёме партии изделий проверяется половина, условие
приёмки – наличие брака менее 2 %. Какова вероятность того, что партия из 100
изделий, содержащая 5% брака, будет принята?
Решение:
Используем формулу Бернулли , в которой положим p= 0,05 ; q=1-0,05=0,95
Проверяем партию из 100/2 =50 изделий, в которой для приема быть не
должно более 50*2%=50*(1/50)=1 бракованной детали, тогда искомая
вероятность
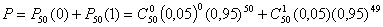 Для вычисления подобной вероятности лучше использовать теорему Лапласа ( n
независимых испытаний с вероятностью появления события p вероятность того, что
событие наступит не менее k и не более m раз равна
Для вычисления подобной вероятности лучше использовать теорему Лапласа ( n
независимых испытаний с вероятностью появления события p вероятность того, что
событие наступит не менее k и не более m раз равна
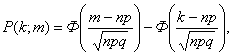 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
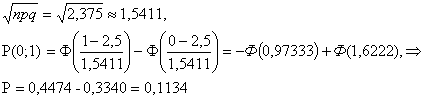 Т.е. искомая вероятность находится в районе 11 %.
ЗАДАЧА № 6 Послан курьер за документами в 4 архива. Вероятность
наличия нужных документа в I-oм архиве – 0,9 ; во II-ом – 0,95; в III-ем – 0,8
; в IV – ом – 0,6.
Найти вероятность Р отсутствия документа только в одном архиве.
Решение: Обозначим заданные вероятности наличия документов
Т.е. искомая вероятность находится в районе 11 %.
ЗАДАЧА № 6 Послан курьер за документами в 4 архива. Вероятность
наличия нужных документа в I-oм архиве – 0,9 ; во II-ом – 0,95; в III-ем – 0,8
; в IV – ом – 0,6.
Найти вероятность Р отсутствия документа только в одном архиве.
Решение: Обозначим заданные вероятности наличия документов 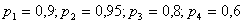 ,тогда вероятности противоположных событий
,тогда вероятности противоположных событий 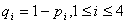 Рассматриваемый случай описывается следующими событиями, описанными ниже в
таблице
Рассматриваемый случай описывается следующими событиями, описанными ниже в
таблице
№ | Не оказалось документа в архиве № | Вероятность 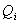 | I | 1 | 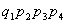
| II | 2 | 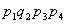
| III | 3 | 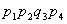
| IV | 4 | 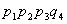
|
По теоремам сложения и умножения вероятностей (для независимых событий)
P=Q1+ Q2+ Q3+ Q4 ,
P= 0,1*0,95*0,8*0,6+0,9*0,05*0,8*0,6+0,9*0,95*0,2*0,6+0,9*0,95*0,8*0,4=0,4434
т.е. 44,34 %
ЗАДАЧА № 7 С 1-го станка на сборку поступает 40 %, со 2-го – 30 %,
с 3-го – 20 %, с 4-го – 10 %. Вероятности брака для каждого из станков 0,1 %,
0,2 %, 0,25 %, 0,5 % соответственно. Найти вероятность Р того, что поступившая
на сборку деталь – бракованная.
Решение: Воспользуемся формулой полной вероятности
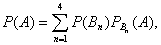 где P(B1)= 0,4 ; P(B2)= 0,3 ; P(B3)= 0,2 ; P(B4)= 0,1
где P(B1)= 0,4 ; P(B2)= 0,3 ; P(B3)= 0,2 ; P(B4)= 0,1 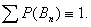 PB1(A)=0,001 ; PB2(A)=0,002; PB3(A)=0,0025; PB4(A)=0,005. (А – событие
состоящее в том, что поступившая деталь на сборку бракованная)
Р= 0,4*0,001+0,3*0,002+0,2*0,0025+0,1*0,005=0,002 = 0,2 %.
ЗАДАЧА № 8 Для участия в спорт. соревнованиях из 1-ой группы было
выделено 4 студента; из 2-ой -6 ; из 3-й – 5 студентов. Вероятность того, что
студент каждый из групп попадает в сборную института равны 0,5 ; 0,4; 0,3
соотв. для каждой из групп. Наудачу выбранный участник попал в сборную. К какой
из 3-х групп он вероятнее всего принадлежит?
Решение: Пусть А – событие состоящие в том, что произвольно
выбранный студент попал в сборную . Всего было студентов N=4+6+5=15.
Вероятность принадлежности студента к каждой из групп P(B1)=4/15 ; P(B2)=6/15 ;
P(B3)=5/15.
Вычислим вероятности того, что студент попавший в сборную принадлежит к
той или иной из 3-х групп по формуле Бейеса
PB1(A)=0,001 ; PB2(A)=0,002; PB3(A)=0,0025; PB4(A)=0,005. (А – событие
состоящее в том, что поступившая деталь на сборку бракованная)
Р= 0,4*0,001+0,3*0,002+0,2*0,0025+0,1*0,005=0,002 = 0,2 %.
ЗАДАЧА № 8 Для участия в спорт. соревнованиях из 1-ой группы было
выделено 4 студента; из 2-ой -6 ; из 3-й – 5 студентов. Вероятность того, что
студент каждый из групп попадает в сборную института равны 0,5 ; 0,4; 0,3
соотв. для каждой из групп. Наудачу выбранный участник попал в сборную. К какой
из 3-х групп он вероятнее всего принадлежит?
Решение: Пусть А – событие состоящие в том, что произвольно
выбранный студент попал в сборную . Всего было студентов N=4+6+5=15.
Вероятность принадлежности студента к каждой из групп P(B1)=4/15 ; P(B2)=6/15 ;
P(B3)=5/15.
Вычислим вероятности того, что студент попавший в сборную принадлежит к
той или иной из 3-х групп по формуле Бейеса 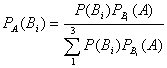 , где в случае нашей задачи PB1(A)=0,5 ; PB2(A)=0,4; PB3(A)=0,3 , учитывая
, где в случае нашей задачи PB1(A)=0,5 ; PB2(A)=0,4; PB3(A)=0,3 , учитывая 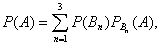
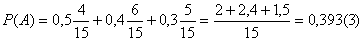 Тогда : Тогда :
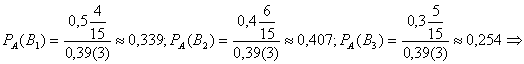 Поскольку 0,407>0,339>0,254 , то вероятнее всего что отобранный студент был из
II-ой группы.
ЗАДАЧА № 9 На автобазе n = 12 автомашин. Вероятность выхода автомашины
на линию равна p=0,8 . Найти вероятность Р нормальной работы автобазы, если для
этого необходимо иметь на линии не менее 8-ми автомашин.
Решение: Для вычисления подобной вероятности лучше
использовать теорему Лапласа ( n независимых испытаний с вероятностью
появления события p вероятность того, что событие наступит не менее k и не
более m раз равна
Поскольку 0,407>0,339>0,254 , то вероятнее всего что отобранный студент был из
II-ой группы.
ЗАДАЧА № 9 На автобазе n = 12 автомашин. Вероятность выхода автомашины
на линию равна p=0,8 . Найти вероятность Р нормальной работы автобазы, если для
этого необходимо иметь на линии не менее 8-ми автомашин.
Решение: Для вычисления подобной вероятности лучше
использовать теорему Лапласа ( n независимых испытаний с вероятностью
появления события p вероятность того, что событие наступит не менее k и не
более m раз равна
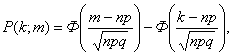 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Где
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Где
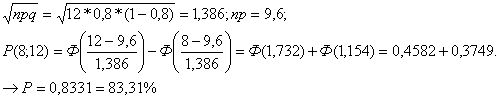 ЗАДАЧА № 10 Пусть вероятность того, что в течении гарантийного срока
телевизор потребует ремонта р=0,2 . Найти вероятность того, что из 6-ти
телевизоров
А) не более одного потребует ремонта;
Б) хотя бы один потребует ремонт.
Решение:
Используем формулу Бернулли :
ЗАДАЧА № 10 Пусть вероятность того, что в течении гарантийного срока
телевизор потребует ремонта р=0,2 . Найти вероятность того, что из 6-ти
телевизоров
А) не более одного потребует ремонта;
Б) хотя бы один потребует ремонт.
Решение:
Используем формулу Бернулли : 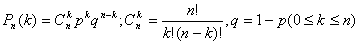 В нашем случае p =0,2 ; q=1-0,2 = 0,8; n=6
Тогда
В нашем случае p =0,2 ; q=1-0,2 = 0,8; n=6
Тогда
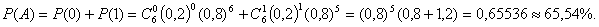
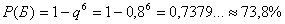 ЗАДАЧА № 11 Вероятность рождения мальчика р=0,515 . Какова
вероятность того, что среди 1000 новорожденных будет 480 девочек?
Решение:
Здесь лучше всего использовать локальную теорему Лапласа ( n независимых
испытаний с вероятностью появления события p вероятность того, что событие
наступит к раз)
ЗАДАЧА № 11 Вероятность рождения мальчика р=0,515 . Какова
вероятность того, что среди 1000 новорожденных будет 480 девочек?
Решение:
Здесь лучше всего использовать локальную теорему Лапласа ( n независимых
испытаний с вероятностью появления события p вероятность того, что событие
наступит к раз)
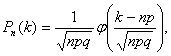 где
где  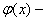 приведенная таблично (см. прил.) функция. приведенная таблично (см. прил.) функция.
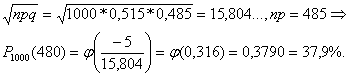 ЗАДАЧА № 12 Процент отсева среди студентов первокурсников составляет 10 %.
Найти вероятность того, что из 900 будет отчислено от 80 до 110 студентов
(включительно)
Решение: Здесь также лучше использовать теорему Лапласа ( n
независимых испытаний с вероятностью появления события p вероятность того, что
событие наступит не менее k и не более m раз равна
ЗАДАЧА № 12 Процент отсева среди студентов первокурсников составляет 10 %.
Найти вероятность того, что из 900 будет отчислено от 80 до 110 студентов
(включительно)
Решение: Здесь также лучше использовать теорему Лапласа ( n
независимых испытаний с вероятностью появления события p вероятность того, что
событие наступит не менее k и не более m раз равна
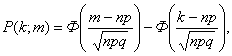 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
У нас n=900 ; p=0,1 ; q=1-0,1=0,9; m=110; k=80;
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
У нас n=900 ; p=0,1 ; q=1-0,1=0,9; m=110; k=80;
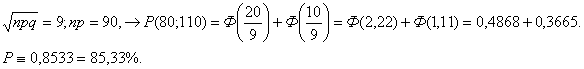 ЗАДАЧА № 13 Вероятность того, что покупателю необходима обувь
41-го размера равна p=0,2 . Найти вероятность того, что из 750 не более 120
потребуют такую обувь.
Решение: Аналогично, здесь тоже лучше применить теорему
Лапласа ( n независимых испытаний с вероятностью появления события p
вероятность того, что событие наступит не менее k и не более m раз равна
ЗАДАЧА № 13 Вероятность того, что покупателю необходима обувь
41-го размера равна p=0,2 . Найти вероятность того, что из 750 не более 120
потребуют такую обувь.
Решение: Аналогично, здесь тоже лучше применить теорему
Лапласа ( n независимых испытаний с вероятностью появления события p
вероятность того, что событие наступит не менее k и не более m раз равна
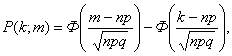 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Положим n =750 ; p=0,2 ; q=1-0,2=0,8; np=150
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Положим n =750 ; p=0,2 ; q=1-0,2=0,8; np=150
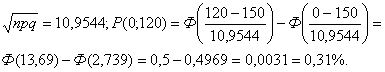 ЗАДАЧА № 14 Вероятность паражения мишени p=0,6 . Найти :
А) границы числа попаданий в мишень при n = 600 выстрелах, чтобы вероятность
невыхода за эти границы была равна
ЗАДАЧА № 14 Вероятность паражения мишени p=0,6 . Найти :
А) границы числа попаданий в мишень при n = 600 выстрелах, чтобы вероятность
невыхода за эти границы была равна 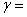 0,993;
Б) такое число m выстрелов по мишени, при котором с вероятностью 0,993 можно
ожидать , что отклонение частоты попаданий от вероятности 0,6 не превзойдет
0,03 (по абсолютной величине).
Решение:
A)
Считая, что число попаданий в цель распределено по нормальному закону , где
0,993;
Б) такое число m выстрелов по мишени, при котором с вероятностью 0,993 можно
ожидать , что отклонение частоты попаданий от вероятности 0,6 не превзойдет
0,03 (по абсолютной величине).
Решение:
A)
Считая, что число попаданий в цель распределено по нормальному закону , где
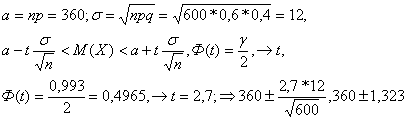 Значит, границы числа попаданий составляют приблизительно (359; 361)
Б) Воспользуемся :
Значит, границы числа попаданий составляют приблизительно (359; 361)
Б) Воспользуемся : 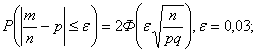
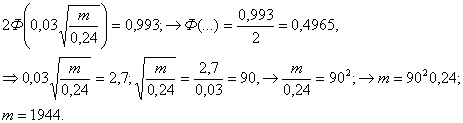 ЗАДАЧА № 15 Мастерская гарантийного ремонта TV обслуживает n=
2000 абонентов. Вероятность того, что купленный TV потребует ремонта равна
р=0,3.
С достоверностью
ЗАДАЧА № 15 Мастерская гарантийного ремонта TV обслуживает n=
2000 абонентов. Вероятность того, что купленный TV потребует ремонта равна
р=0,3.
С достоверностью 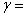 0,9973 найти границы числа телевизоров, потребующих гарантийного ремонта.
Решение:
Считая, что закон распределения телевизоров, требующих ремонта нормальный
находим
0,9973 найти границы числа телевизоров, потребующих гарантийного ремонта.
Решение:
Считая, что закон распределения телевизоров, требующих ремонта нормальный
находим 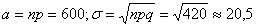
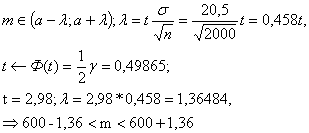 Значит, 599 < m < 601
Значит, 599 < m < 601
|
|
|
|
|

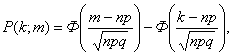 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
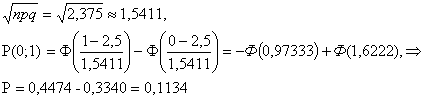 Т.е. искомая вероятность находится в районе 11 %.
ЗАДАЧА № 6 Послан курьер за документами в 4 архива. Вероятность
наличия нужных документа в I-oм архиве – 0,9 ; во II-ом – 0,95; в III-ем – 0,8
; в IV – ом – 0,6.
Найти вероятность Р отсутствия документа только в одном архиве.
Решение: Обозначим заданные вероятности наличия документов
Т.е. искомая вероятность находится в районе 11 %.
ЗАДАЧА № 6 Послан курьер за документами в 4 архива. Вероятность
наличия нужных документа в I-oм архиве – 0,9 ; во II-ом – 0,95; в III-ем – 0,8
; в IV – ом – 0,6.
Найти вероятность Р отсутствия документа только в одном архиве.
Решение: Обозначим заданные вероятности наличия документов 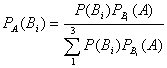 , где в случае нашей задачи PB1(A)=0,5 ; PB2(A)=0,4; PB3(A)=0,3 , учитывая
, где в случае нашей задачи PB1(A)=0,5 ; PB2(A)=0,4; PB3(A)=0,3 , учитывая 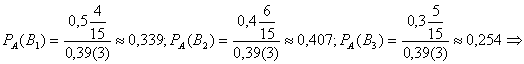 Поскольку 0,407>0,339>0,254 , то вероятнее всего что отобранный студент был из
II-ой группы.
ЗАДАЧА № 9 На автобазе n = 12 автомашин. Вероятность выхода автомашины
на линию равна p=0,8 . Найти вероятность Р нормальной работы автобазы, если для
этого необходимо иметь на линии не менее 8-ми автомашин.
Решение: Для вычисления подобной вероятности лучше
использовать теорему Лапласа ( n независимых испытаний с вероятностью
появления события p вероятность того, что событие наступит не менее k и не
более m раз равна
Поскольку 0,407>0,339>0,254 , то вероятнее всего что отобранный студент был из
II-ой группы.
ЗАДАЧА № 9 На автобазе n = 12 автомашин. Вероятность выхода автомашины
на линию равна p=0,8 . Найти вероятность Р нормальной работы автобазы, если для
этого необходимо иметь на линии не менее 8-ми автомашин.
Решение: Для вычисления подобной вероятности лучше
использовать теорему Лапласа ( n независимых испытаний с вероятностью
появления события p вероятность того, что событие наступит не менее k и не
более m раз равна
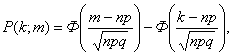 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Где
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Где
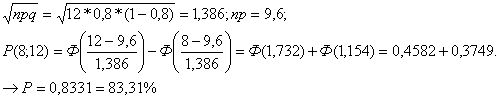 ЗАДАЧА № 10 Пусть вероятность того, что в течении гарантийного срока
телевизор потребует ремонта р=0,2 . Найти вероятность того, что из 6-ти
телевизоров
А) не более одного потребует ремонта;
Б) хотя бы один потребует ремонт.
Решение:
Используем формулу Бернулли :
ЗАДАЧА № 10 Пусть вероятность того, что в течении гарантийного срока
телевизор потребует ремонта р=0,2 . Найти вероятность того, что из 6-ти
телевизоров
А) не более одного потребует ремонта;
Б) хотя бы один потребует ремонт.
Решение:
Используем формулу Бернулли : 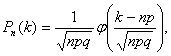 где
где 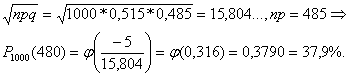 ЗАДАЧА № 12 Процент отсева среди студентов первокурсников составляет 10 %.
Найти вероятность того, что из 900 будет отчислено от 80 до 110 студентов
(включительно)
Решение: Здесь также лучше использовать теорему Лапласа ( n
независимых испытаний с вероятностью появления события p вероятность того, что
событие наступит не менее k и не более m раз равна
ЗАДАЧА № 12 Процент отсева среди студентов первокурсников составляет 10 %.
Найти вероятность того, что из 900 будет отчислено от 80 до 110 студентов
(включительно)
Решение: Здесь также лучше использовать теорему Лапласа ( n
независимых испытаний с вероятностью появления события p вероятность того, что
событие наступит не менее k и не более m раз равна
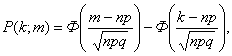 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
У нас n=900 ; p=0,1 ; q=1-0,1=0,9; m=110; k=80;
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
У нас n=900 ; p=0,1 ; q=1-0,1=0,9; m=110; k=80;
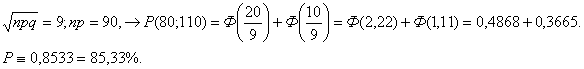 ЗАДАЧА № 13 Вероятность того, что покупателю необходима обувь
41-го размера равна p=0,2 . Найти вероятность того, что из 750 не более 120
потребуют такую обувь.
Решение: Аналогично, здесь тоже лучше применить теорему
Лапласа ( n независимых испытаний с вероятностью появления события p
вероятность того, что событие наступит не менее k и не более m раз равна
ЗАДАЧА № 13 Вероятность того, что покупателю необходима обувь
41-го размера равна p=0,2 . Найти вероятность того, что из 750 не более 120
потребуют такую обувь.
Решение: Аналогично, здесь тоже лучше применить теорему
Лапласа ( n независимых испытаний с вероятностью появления события p
вероятность того, что событие наступит не менее k и не более m раз равна
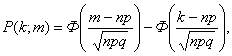 где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Положим n =750 ; p=0,2 ; q=1-0,2=0,8; np=150
где Ф(.) – затабулированная функция Лапласа (см. справочное приложение))
Положим n =750 ; p=0,2 ; q=1-0,2=0,8; np=150
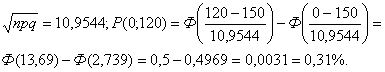 ЗАДАЧА № 14 Вероятность паражения мишени p=0,6 . Найти :
А) границы числа попаданий в мишень при n = 600 выстрелах, чтобы вероятность
невыхода за эти границы была равна
ЗАДАЧА № 14 Вероятность паражения мишени p=0,6 . Найти :
А) границы числа попаданий в мишень при n = 600 выстрелах, чтобы вероятность
невыхода за эти границы была равна 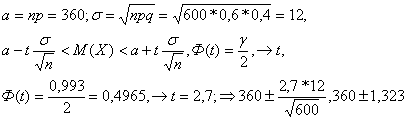 Значит, границы числа попаданий составляют приблизительно (359; 361)
Б) Воспользуемся :
Значит, границы числа попаданий составляют приблизительно (359; 361)
Б) Воспользуемся : 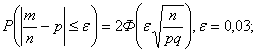
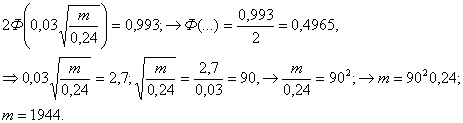 ЗАДАЧА № 15 Мастерская гарантийного ремонта TV обслуживает n=
2000 абонентов. Вероятность того, что купленный TV потребует ремонта равна
р=0,3.
С достоверностью
ЗАДАЧА № 15 Мастерская гарантийного ремонта TV обслуживает n=
2000 абонентов. Вероятность того, что купленный TV потребует ремонта равна
р=0,3.
С достоверностью 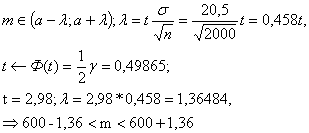 Значит, 599 < m < 601
Значит, 599 < m < 601
