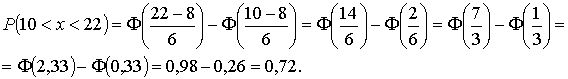|
|
|
|
Контрольная: Контрольная по теории вероятности
Контрольная: Контрольная по теории вероятности
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ
Факультет заочного и послевузовского обучения
КОНТРОЛЬНАЯ РАБОТА №1
По дисциплине: "Теория вероятностей и элементы математической статистики"
Воронеж 2004 г.
Вариант – 9.
Задача № 1.
№№ 1-20. Техническое устройство, состоящее из трех узлов, работало в
течение некоторого времени t. За это время первый узел оказывается неисправным
с вероятностью р1, второй – с вероятностью р2, третий – с
вероятностью р3. Найти вероятность того, что за время работы: а) все
узлы оставались исправными; б) все узлы вышли из строя; в) только один узел
стал неисправным; г) хотя бы один узел стал неисправным (см. исходные данные в
таблице).
p1=0,4 p2=0,6 p3=0,9
Решение:
Пусть событие А означает, что первый узел оказался неисправным, В
оказался неисправным второй узел и С – оказался неисправным третий узел,
тогда 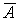 - первый
узел был исправен в промежуток времени t, - первый
узел был исправен в промежуток времени t, 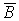 - был исправен второй узел,
- был исправен второй узел, 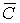 - был исправен третий узел.
а) Пусть событие D означает, что все узлы оставались исправными, тогда
- был исправен третий узел.
а) Пусть событие D означает, что все узлы оставались исправными, тогда 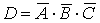 . Поэтому , учитывая независимость событий
. Поэтому , учитывая независимость событий 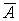 ,
, 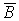 и и 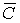 , по теореме умножения вероятностей имеем:
, по теореме умножения вероятностей имеем:
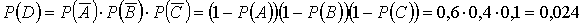 б) Пусть событие Е – все узлы вышли из строя, тогда:
б) Пусть событие Е – все узлы вышли из строя, тогда:
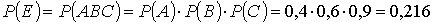 в) Пусть событие F – только один узел стал неисправным, тогда:
в) Пусть событие F – только один узел стал неисправным, тогда:
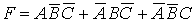 События
События 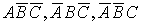 несовместные. Поэтому, применяя теорему сложения вероятностей несовместимых
событий, получим:
несовместные. Поэтому, применяя теорему сложения вероятностей несовместимых
событий, получим:
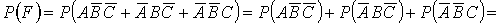
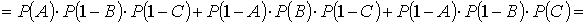
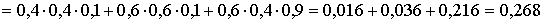 г) Пусть событие D1 – хотя бы один узел стал неисправным, тогда:
г) Пусть событие D1 – хотя бы один узел стал неисправным, тогда:
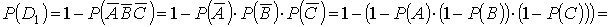
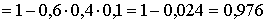 . .
Задача № 2
№39. По линии связи могут быть переданы символы А, В, С. Вероятность передачи
символа А равна 0,5; символа В – 0,3; символа С – 0,2. Вероятности искажения
при передаче символов А, В, С равны соответственно 0,01; 0,03; 0,07.
Установлено, что сигнал из двух символов принят без искажения. Чему равна
вероятность, что передавался сигнал АВ?
Решение:
Пусть событие А – передача символа А, событие В – передача символа В, событие С
– передача символа С, событие 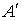 - искажение при передаче символа А, событие
- искажение при передаче символа А, событие 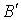 и
и 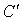 - искажения при
передаче символов В и С соответственно.
По условию вероятности этих событий равны: - искажения при
передаче символов В и С соответственно.
По условию вероятности этих событий равны:
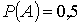 , , 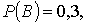 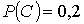 , , 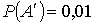 , , 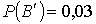 , , 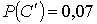 Если события
Если события 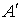 , , 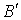 и
и 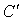 - искажения при
передаче символов, то события - искажения при
передаче символов, то события 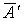 ,
, 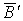 и и 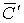 - отсутствие искажений при передаче. Их вероятности:
- отсутствие искажений при передаче. Их вероятности:
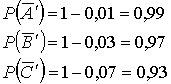 Обозначим через D событие, состоящее в том, что были переданы два символа без
искажений.
Можно выдвинуть следующие гипотезы:
Н1 – переданы символы АА,
Н2 – символы АВ,
Н3 – символы ВА,
Н4 – символы АС,
Н5 – символы СА,
Н6 – символы ВВ,
Н7 – символы ВС,
Н8 – символы СВ,
Н9 – символы СС.
Вероятности этих гипотез:
Обозначим через D событие, состоящее в том, что были переданы два символа без
искажений.
Можно выдвинуть следующие гипотезы:
Н1 – переданы символы АА,
Н2 – символы АВ,
Н3 – символы ВА,
Н4 – символы АС,
Н5 – символы СА,
Н6 – символы ВВ,
Н7 – символы ВС,
Н8 – символы СВ,
Н9 – символы СС.
Вероятности этих гипотез:
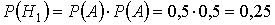
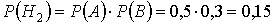
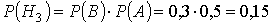
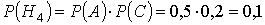
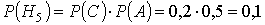
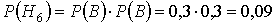
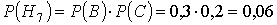
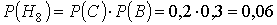
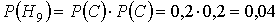 Условные вероятности события D если имела место одна из гипотез будут:
Условные вероятности события D если имела место одна из гипотез будут:
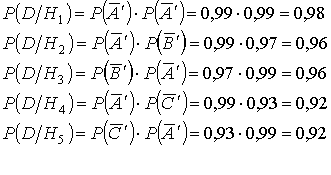
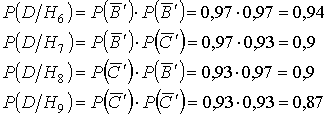 По формуле Бейеса вычислим условную вероятность
По формуле Бейеса вычислим условную вероятность 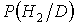 с учетом появления события Р: с учетом появления события Р:
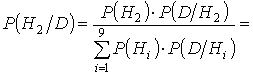
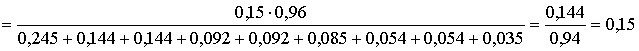 Задача № 3
№№ 41-60. Найти вероятность того, что в п независимых испытаниях событие
появится: а) ровно k раз; б) не менее k раз; в) не более k раз; г) хотя бы один
раз, если в каждом испытании вероятность появления этого события равна р (см.
исходные данные в таблице).
Решение:
Так как число испытаний невелико, то для вычисления искомой вероятности
воспользуемся формулой Бернулли:
Задача № 3
№№ 41-60. Найти вероятность того, что в п независимых испытаниях событие
появится: а) ровно k раз; б) не менее k раз; в) не более k раз; г) хотя бы один
раз, если в каждом испытании вероятность появления этого события равна р (см.
исходные данные в таблице).
Решение:
Так как число испытаний невелико, то для вычисления искомой вероятности
воспользуемся формулой Бернулли:
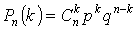 , где , где
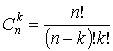 число сочетаний из п элементов по k, q=1-p. В рассматриваемом случае:
а) вероятность появления события ровно 4 раза в 5 испытаниях:
число сочетаний из п элементов по k, q=1-p. В рассматриваемом случае:
а) вероятность появления события ровно 4 раза в 5 испытаниях:
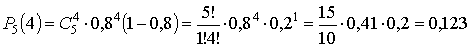 б) вероятность появления события не менее 4 раз в 5 испытаниях:
б) вероятность появления события не менее 4 раз в 5 испытаниях:
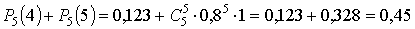 в) вероятность появления события не более 4 раз в 5 испытаниях:
в) вероятность появления события не более 4 раз в 5 испытаниях:
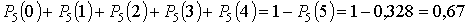 г) вероятность появления события хотя бы один раз в 5 испытаниях:
г) вероятность появления события хотя бы один раз в 5 испытаниях:
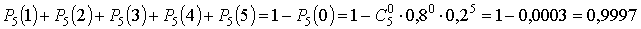
Задача № 4
№№ 61-80. Дана плотность распределения f(x) случайной величины Х. Найти
параметр а, функцию распределения случайной величины, математическое ожидание
М[Х], дисперсию D[X], вероятность выполнения неравенства х1<x<
x2, построить график функции распределения F(x).
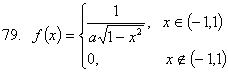 Решение:
Для определения параметра а воспользуемся основным свойством плотности
распределения:
Решение:
Для определения параметра а воспользуемся основным свойством плотности
распределения:
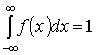 , так как при , так как при 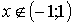 плотность распределения равна нулю, то интеграл примет вид:
плотность распределения равна нулю, то интеграл примет вид: 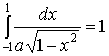 или
или 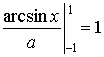 , откуда , откуда
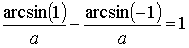 ; ; 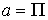 Функция распределения связана с функцией плотности соотношением:
Функция распределения связана с функцией плотности соотношением:
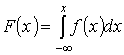 Откуда получим:
Откуда получим: 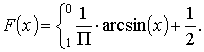 Математическое ожидание
Математическое ожидание 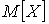 и дисперсию и дисперсию 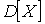 определим по формулам: определим по формулам:
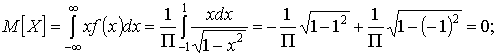
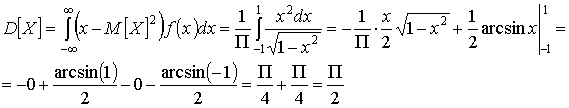 Вероятность выполнения неравенства <x< определим по
формуле: Р( <x< )=
Вероятность выполнения неравенства <x< определим по
формуле: Р( <x< )=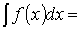 F( ) – F( )=
F( ) – F( )=
Задача №5
№№ 81-100. Найти вероятность попадания в заданный интервал 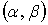 нормально распределенной случайной величины, если известны ее математическое
ожидание а и среднее квадратическое отклонение
нормально распределенной случайной величины, если известны ее математическое
ожидание а и среднее квадратическое отклонение 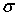 (см. исходные данные в таблице).
Решение:
Для определения искомой вероятности воспользуемся формулой:
(см. исходные данные в таблице).
Решение:
Для определения искомой вероятности воспользуемся формулой:
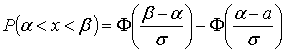 Здесь
Здесь 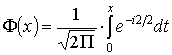 - функция
Ломпаса, значения которой определяются по таблице. Учитывая, что функция
Ф(х) нечетная, получим: - функция
Ломпаса, значения которой определяются по таблице. Учитывая, что функция
Ф(х) нечетная, получим:
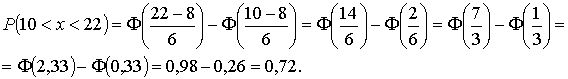
|
|
|
|
|

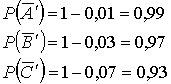 Обозначим через D событие, состоящее в том, что были переданы два символа без
искажений.
Можно выдвинуть следующие гипотезы:
Н1 – переданы символы АА,
Н2 – символы АВ,
Н3 – символы ВА,
Н4 – символы АС,
Н5 – символы СА,
Н6 – символы ВВ,
Н7 – символы ВС,
Н8 – символы СВ,
Н9 – символы СС.
Вероятности этих гипотез:
Обозначим через D событие, состоящее в том, что были переданы два символа без
искажений.
Можно выдвинуть следующие гипотезы:
Н1 – переданы символы АА,
Н2 – символы АВ,
Н3 – символы ВА,
Н4 – символы АС,
Н5 – символы СА,
Н6 – символы ВВ,
Н7 – символы ВС,
Н8 – символы СВ,
Н9 – символы СС.
Вероятности этих гипотез:
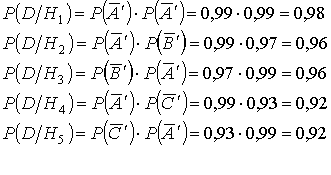
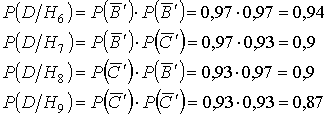 По формуле Бейеса вычислим условную вероятность
По формуле Бейеса вычислим условную вероятность 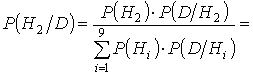
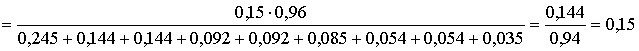 Задача № 3
№№ 41-60. Найти вероятность того, что в п независимых испытаниях событие
появится: а) ровно k раз; б) не менее k раз; в) не более k раз; г) хотя бы один
раз, если в каждом испытании вероятность появления этого события равна р (см.
исходные данные в таблице).
Задача № 3
№№ 41-60. Найти вероятность того, что в п независимых испытаниях событие
появится: а) ровно k раз; б) не менее k раз; в) не более k раз; г) хотя бы один
раз, если в каждом испытании вероятность появления этого события равна р (см.
исходные данные в таблице).
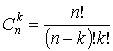 число сочетаний из п элементов по k, q=1-p. В рассматриваемом случае:
а) вероятность появления события ровно 4 раза в 5 испытаниях:
число сочетаний из п элементов по k, q=1-p. В рассматриваемом случае:
а) вероятность появления события ровно 4 раза в 5 испытаниях:
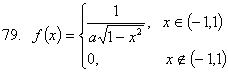 Решение:
Для определения параметра а воспользуемся основным свойством плотности
распределения:
Решение:
Для определения параметра а воспользуемся основным свойством плотности
распределения:
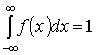 , так как при
, так как при 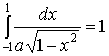 или
или 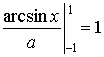 , откуда
, откуда
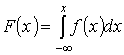 Откуда получим:
Откуда получим: 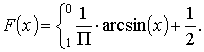 Математическое ожидание
Математическое ожидание 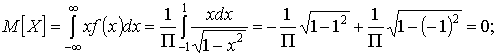
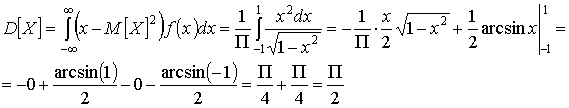 Вероятность выполнения неравенства <x< определим по
формуле: Р( <x< )=
Вероятность выполнения неравенства <x< определим по
формуле: Р( <x< )=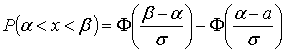 Здесь
Здесь 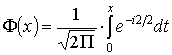 - функция
Ломпаса, значения которой определяются по таблице. Учитывая, что функция
Ф(х) нечетная, получим:
- функция
Ломпаса, значения которой определяются по таблице. Учитывая, что функция
Ф(х) нечетная, получим: