|
|
|
|
Контрольная: Контрольная работа по теории вероятности_2
Контрольная: Контрольная работа по теории вероятности_2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ
Факультет заочного и послевузовского обучения
КОНТРОЛЬНАЯ РАБОТА №2
По дисциплине: "Теория вероятностей и элементы математической статистики"
Воронеж 2004 г.
Вариант – 9.
Задача № 1
1-20. Найти методом произведений: а) выборочную среднюю; б) выборочную
дисперсию; в) выборочное среднее квадратическое отклонение по данному
статистическому распределению выборки (в первой строке указаны выборочные
варианты хi, а во второй соответственные частоты ni
количественного признака Х).
| 19. | xi | 14,5 | 24,5 | 34,4 | 44,4 | 54,4 | 64,4 | 74,4 | ni | 5 | 15 | 40 | 25 | 8 | 4 | 3 |
Решение:
Составим расчетную таблицу 1, для этого:
1) запишем варианты в первый столбец;
2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю
клетку столбца;
3) в качестве ложного нуля С выберем варианту 34,5, которая имеет
наибольшую частоту; в клетке третьего столбца, которая принадлежит строке,
содержащей ложный нуль, пишем 0; над нулем последовательно записываем –1, -2, а
над нулем 1, 2, 3;
4) произведения частот ni на условные варианты ui
запишем в четвертый столбец; отдельно находим сумму (-25) отрицательных чисел и
отдельную сумму (65) положительных чисел; сложив эти числа, их сумму (40)
помещаем в нижнюю клетку четвертого столбца;
5) произведения частот на квадраты условных вариант, т. е. 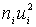 , запишем в пятый столбец; сумму чисел столбца (176) помещаем в нижнюю клетку
пятого столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, т.
е.
, запишем в пятый столбец; сумму чисел столбца (176) помещаем в нижнюю клетку
пятого столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, т.
е. 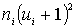 запишем в
шестой контрольный столбец; сумму чисел столбца (356) помещаем в нижнюю клетку
шестого столбца.
В итоге получим расчетную таблицу 1.
Для контроля вычислений пользуются тождеством запишем в
шестой контрольный столбец; сумму чисел столбца (356) помещаем в нижнюю клетку
шестого столбца.
В итоге получим расчетную таблицу 1.
Для контроля вычислений пользуются тождеством
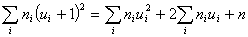 .
Контроль: .
Контроль: 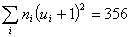 ; ;
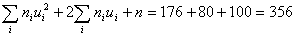 .
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого и второго порядков: .
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого и второго порядков:
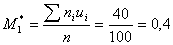 ; ;
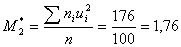 .
Найдем шаг (разность между любыми двумя соседними вариантами): .
Найдем шаг (разность между любыми двумя соседними вариантами): 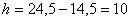 .
Вычислим искомые выборочные среднюю и дисперсию, учитывая, что ложный нуль
(варианта, которая имеет наибольшую частоту) С=34,5: .
Вычислим искомые выборочные среднюю и дисперсию, учитывая, что ложный нуль
(варианта, которая имеет наибольшую частоту) С=34,5:
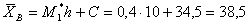
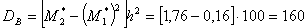 в) выборочное среднее квадратичное отклонение:
в) выборочное среднее квадратичное отклонение:
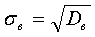
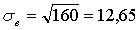 Таблица 1.
Таблица 1.
| 1 | 2 | 3 | 4 | 5 | 6 | xi | ni | ui | niui | 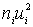
| 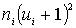
| | 14,5 | 5 | -2 | -10 | 20 | 5 | | 24,5 | 15 | -1 | -15 | 15 | - | | 34,5 | 40 | 0 | -25 | - | 40 | | 44,5 | 25 | 1 | 25 | 25 | 100 | | 54,5 | 8 | 2 | 16 | 32 | 72 | | 64,5 | 4 | 3 | 12 | 36 | 64 | | 74,5 | 3 | 4 | 12 | 48 | 75 | | | | 65 | | | | п=100 | | 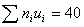
| 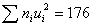
| 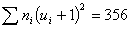
|
Задача №2
№№ 21-40. Найти доверительные интервалы для оценки математического
ожидания 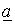 нормального
распределения с надежностью 0,95, зная выборочную среднюю нормального
распределения с надежностью 0,95, зная выборочную среднюю 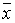 , объем выборки
, объем выборки 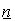 и среднее
квадратическое отклонение и среднее
квадратическое отклонение 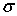 . .
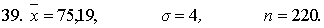 Решение:
Требуется найти доверительный интервал
Решение:
Требуется найти доверительный интервал
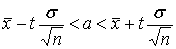 (*)
Все величины, кроме t, известны. Найдем t из соотношения (*)
Все величины, кроме t, известны. Найдем t из соотношения 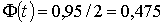 . По таблице приложения 2 [1] находим t=1,96. Подставим в неравенство
t=1,96,
. По таблице приложения 2 [1] находим t=1,96. Подставим в неравенство
t=1,96, 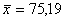 , , 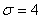 , п=220 в (*).
Окончательно получим искомый доверительный интервал
, п=220 в (*).
Окончательно получим искомый доверительный интервал
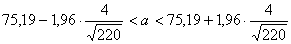
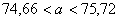
|
|
|
|
|

