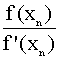|
|
|
|
Курсовая: Исчисления методами Лагранжа Рунге Кутта Ньютона и Гаусса
Курсовая: Исчисления методами Лагранжа Рунге Кутта Ньютона и Гаусса

КУРСОВОЙ ПРОЕКТ
по дисциплине «Информатика»
студента группы КС-31
Кузнецова Дмитрия Олеговича
  СОДЕРЖАНИЕ
ВВЕДЕНИЕ
2
1.Задача 1
1.1 Постановка задачи
1.2 Решение
4
2. Задача 2
2.1.Постановка задачи
2.2.Решение
6
3.Задача 3
3.1.Постановка задачи
3.2.Решение
10
4.Задача 4
4.1.Постановка задачи
4.2.Решение
15
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
2
1.Задача 1
1.1 Постановка задачи
1.2 Решение
4
2. Задача 2
2.1.Постановка задачи
2.2.Решение
6
3.Задача 3
3.1.Постановка задачи
3.2.Решение
10
4.Задача 4
4.1.Постановка задачи
4.2.Решение
15
СПИСОК ЛИТЕРАТУРЫ 16
ВВЕДЕНИЕ
Основой автоматизации умственного труда человека является широкое внедрение
вычислительной техники во все сферы деятельности человека . Применение ЭВМ
ускорило процесс математизации науки и техники . Расширяется круг профессий
,для которых математическая грамотность и наличие практических навыков
применения ЭВМ становятся необходимыми.
Решение технической или научной задачи включает её математическое описание на
языке уравнений, функций .Очень часто математическая формулировка задачи
может оказаться непереводимой на язык ЭВМ ,так как ЭВМ выполняет только
арифметические действия.
Численный метод решения задачи –это определённая последовательность операций
над числами , язык которого числа и арифметические действия .Численные методы
легко реализуются на ЭВМ ,что делает эти методы мощным и универсальным
инструментом. Процесс решения инженерной задачи на ЭВМ сложный и длительный
.Он включает в себя этапы, требующие от разработчика профессиональной
подготовки и грамотности. Для снижения трудоёмкости , на всех типах ЭВМ
создан мощный аппарат технологической поддержки работы пользователя ЭВМ.
1.Задача 1
1.1.Постановка задачи
Необходимо графически определить один корень уравнения . Уточнить корень
уравнения с точностью Е=0,001 методом Ньютона. Дано нелинейное уравнение :
tg(ax+b)=x2
где a=0,5 и b=0,2
1.2.Решение
Для того ,чтобы определить корень ,преобразуем уравнение к виду :
tg(0.5x+0.2)=x2
Построим графики двух функций :
y1= tg(0.5x+0.2) и y2=x2;
Кривые на рис.1 описаны следующим образом:
1) y1= tg(0.5x+0.2) функция периодическая ,её значения сведём в таблицу 1.1
Таблица 1.1.
| x | -3.1 | -3 | -2 | -1 | 0 | 1 | 2 | 2.1 | 2.2 | | y | -4.45 | -2.57 | -1.02 | -0,3 | 0,2 | 0,84 | 2.57 | 3.0 | 3.6 |
2) y2=x2 – парабола
y2=0 когда x=0
y2=4 при x=±2
По графику определяем ,что уравнение имеет несколько корней .Для уточнения
корня выберем интервал [0,1] .Уточняем корень по формуле Ньютона:
xn+1= xn- 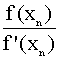 Необходимо выбрать начальное значение x0 , исходя из условия сходимости:
f(x0)f "(x0)>0
f(x)= tg(0.5x+0.2) – x2
Необходимо выбрать начальное значение x0 , исходя из условия сходимости:
f(x0)f "(x0)>0
f(x)= tg(0.5x+0.2) – x2
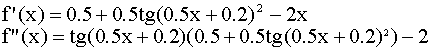 Проверяем условия сходимости для x=0 :
Проверяем условия сходимости для x=0 :
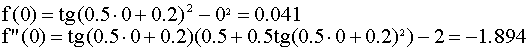 f(0)f"(0)<0,условие не соблюдается
f(0)f"(0)<0,условие не соблюдается  Проверяем условие сходимости для x=1.0 :
Проверяем условие сходимости для x=1.0 :
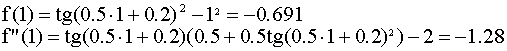 f(0)f"(0)>0,условие соблюдается
берём за x0=1
и условие:
Т=
f(0)f"(0)>0,условие соблюдается
берём за x0=1
и условие:
Т=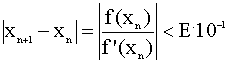 Решение запишем в виде таблицы:
Решение запишем в виде таблицы:
| n | x n | f(x n) | f '(x n) | 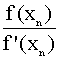
| T<E 10-1 | | 0 | 1.000000 | -0.158000 | -1.151000 | 0.137271 | Нет | | 1 | 0.862728 | -0.013000 | -0.976000 | 0.013119 | Нет | | 2 | 0.849416 | -0.000467 | -0.958000 | 0.000487 | Нет | | 3 | 0.848929 | -0.000009 | -0.958000 | 0.000009 | Да | | 4 | 0.848920 | | | | |
В результате проделанной работы мы определили один корень уравнения вида
tg(0.5x+0.2)=x2 графически,а затем уточнили его методом Ньютона и
получили
X=0.848929
Вывод по решению:
В результате проделанной работы мы определили один корень уравнения
Tg(0.5x+0.2)=x2 графически, а затем уточнили его методом Ньютона и
получили x=0.848929
2.Задача 2
2.1.Постановка задачи
Выбрать формулу интерполяции и с её помощью определить значение функции в
точке x=0,38.Функция задана в виде таблицы 2.1 ,Степень интерполяционного
многочлена равна 3.
Таблица 2.1
| 0,15 | 0,860708 | | 0,25 | 0,778801 | | 0,30 | 0,740818 | | 0,40 | 0,670320 | | 0,45 | 0,637628 | | 0,55 | 0,576950 | | 0,60 | 0,548812 | | 0,65 | 0,522046 | | 0,70 | 0,496585 | | 0,75 | 0,472237 |
2.2.Решение
Решение будем производить методом Лагранжа.Oцениваем шаг
h=xi+1 -xi
В этой таблице h=const.Для интерполяции функции с произвольно задаными узлами
выбираем интерполяционный многочлен Лагранжа:
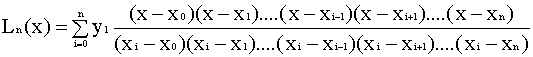 ;
Выражения,называемые коэффициентами Лагранжа:
;
Выражения,называемые коэффициентами Лагранжа:
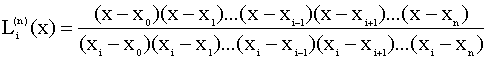 Далее построим матрицу Лагранжа:
Далее построим матрицу Лагранжа:
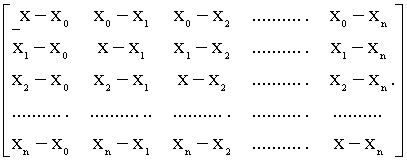 Обозначим произведение строк через
Обозначим произведение строк через 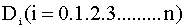 ,а произведение элементов главной диагонали через
,а произведение элементов главной диагонали через 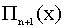 ,тогда :
,тогда :
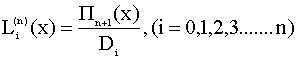
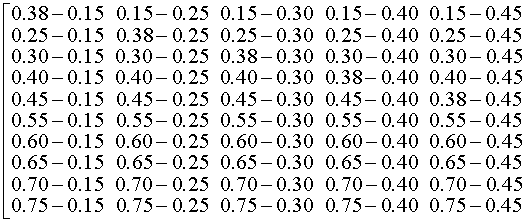
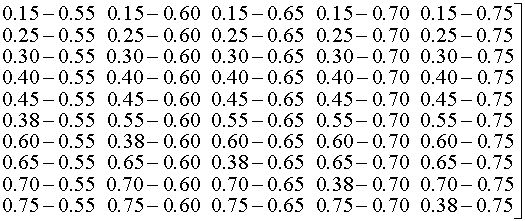 Вычислим её:
Вычислим её:
 
 отсюда:
Пn+1=4,00384 .10-9
D0=7,68488.10-6 D5=1.1475.10-8
D1=-1.84275.10-7 D6= -1.16944.10-8
D2= 4.2525.10-8 D7=2.3625.10-8
D3=2.92313 10-9 D8= -8.91.10-8
D4= -7.0875.10-9 D9=7.86713.10-7
отсюда:
Пn+1=4,00384 .10-9
D0=7,68488.10-6 D5=1.1475.10-8
D1=-1.84275.10-7 D6= -1.16944.10-8
D2= 4.2525.10-8 D7=2.3625.10-8
D3=2.92313 10-9 D8= -8.91.10-8
D4= -7.0875.10-9 D9=7.86713.10-7
Далее по формуле:
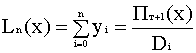 ,
имеем ,
имеем
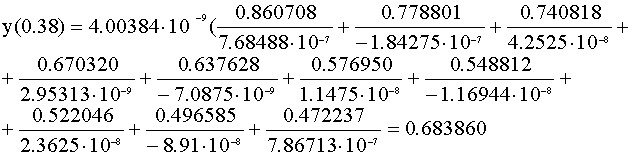 В результате проделанной работы мы произвели интерполяцию функции заданной
таблицей 2.1 и получили значение функции в точке х=0,38 y=0,683860.
О справедливости полученного результата мы можем судить из того ,что точка
х=0,38 находиться точками х=0,30 и х=0,40 и искомое значение должно
находиться между соответствующими значениями этих точек. Полученное значение
y=0,683860 находиться в пределах между y(0.30)=0.670320 и y(0.40)=0.740818.
Следовательно решение верно.
3.Задача 3
3.1.Постановка задачи
В результате проделанной работы мы произвели интерполяцию функции заданной
таблицей 2.1 и получили значение функции в точке х=0,38 y=0,683860.
О справедливости полученного результата мы можем судить из того ,что точка
х=0,38 находиться точками х=0,30 и х=0,40 и искомое значение должно
находиться между соответствующими значениями этих точек. Полученное значение
y=0,683860 находиться в пределах между y(0.30)=0.670320 и y(0.40)=0.740818.
Следовательно решение верно.
3.Задача 3
3.1.Постановка задачи
 Решить систему линейных уравнений: Решить систему линейных уравнений:
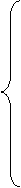 9.3x1+(1.62+a)x2+6.1x3+1.9x4=-12.65+b;
4.92x1+7.45x2+(9.7-a)x3+2.46x4=10.21;
4.77x1+(6.21+a)x2+9.04x3+2.28x4=13.45;
3.21x1+(2.65-a)x2+3.69x3+6.99x4=-10.35.
методом Гаусса. Все расчёты ведите с тремя значащими цифрами после запятой.
2)Результаты вычисления прямого хода представьте в виде таблицы с контролем в
виде суммирующего столбца. Вычисления обратного хода сделайте подробно,
записав все промежуточные вычисления.
3.2.Решение
Перепишем систему линейных уравнений в виде:
9.3x1+(1.62+a)x2+6.1x3+1.9x4=-12.65+b;
4.92x1+7.45x2+(9.7-a)x3+2.46x4=10.21;
4.77x1+(6.21+a)x2+9.04x3+2.28x4=13.45;
3.21x1+(2.65-a)x2+3.69x3+6.99x4=-10.35.
методом Гаусса. Все расчёты ведите с тремя значащими цифрами после запятой.
2)Результаты вычисления прямого хода представьте в виде таблицы с контролем в
виде суммирующего столбца. Вычисления обратного хода сделайте подробно,
записав все промежуточные вычисления.
3.2.Решение
Перепишем систему линейных уравнений в виде:
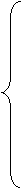 9.3x1+(1.62+0.8)x2+6.1x3+1.9x4=-12.65+3.6;
4.92x1+7.45x2+(9.7-0.8)x3+2.46x4=10.21;
4.77x1+(6.21+0.8)x2+9.04x3+2.28x4=13.45;
3.21x1+(2.65-0.8)x2+3.69x3+6.99x4=-10.35.
9.3x1+(1.62+0.8)x2+6.1x3+1.9x4=-12.65+3.6;
4.92x1+7.45x2+(9.7-0.8)x3+2.46x4=10.21;
4.77x1+(6.21+0.8)x2+9.04x3+2.28x4=13.45;
3.21x1+(2.65-0.8)x2+3.69x3+6.99x4=-10.35.
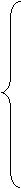 9.3x1+2.42x2+6.1x3+1.9x4=-9.05;
4.92x1+7.45x2+8.9x3+2.46x4=10.21;
4.77x1+7.01x2+9.04x3+2.28x4=13.45;
3.21x1+1.85x2+3.69x3+6.99x4=-10.35.
Введём обозначение:
9.3x1+2.42x2+6.1x3+1.9x4=-9.05;
4.92x1+7.45x2+8.9x3+2.46x4=10.21;
4.77x1+7.01x2+9.04x3+2.28x4=13.45;
3.21x1+1.85x2+3.69x3+6.99x4=-10.35.
Введём обозначение: или или а15,а25,а35,а45---свободные члены
а15,а25,а35,а45---свободные члены
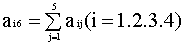 ---суммирующий (контрольный) коэффициент
Прямой ход. Заполнение таблицы:
1.Запишем аij в четырёх строках и пяти столбцах раздела 1
таблицы(i=1,2,3,4,j=1,2,3,4,5)
2.Стимулирующие аi6 запишем в столбце å (столбец контроля)
3.Вычисляем b1j=a1j/a11 (j=1,2,3,..6) и запишем в пятой строке раздела 1
4.Вычисляем ---суммирующий (контрольный) коэффициент
Прямой ход. Заполнение таблицы:
1.Запишем аij в четырёх строках и пяти столбцах раздела 1
таблицы(i=1,2,3,4,j=1,2,3,4,5)
2.Стимулирующие аi6 запишем в столбце å (столбец контроля)
3.Вычисляем b1j=a1j/a11 (j=1,2,3,..6) и запишем в пятой строке раздела 1
4.Вычисляем 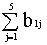 и
проверяем совпала ли она с b16 c вычисления ведутся с постоянным
количеством знаков после запятой). В противном случае проверяем действия
пункта 3.
5.Вычисляем b1ij(1)=aij-ai1.
b1j(i=2,3,4 , j=2,3,..6) и записываем их в в первые три строки
раздела 2.
6.Проверка. Сумма элементов каждой строки и
проверяем совпала ли она с b16 c вычисления ведутся с постоянным
количеством знаков после запятой). В противном случае проверяем действия
пункта 3.
5.Вычисляем b1ij(1)=aij-ai1.
b1j(i=2,3,4 , j=2,3,..6) и записываем их в в первые три строки
раздела 2.
6.Проверка. Сумма элементов каждой строки 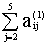 и
и 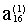 должен совпасть с
указанной в п.4 точностью, иначе надо проверить п.5.
7.Вычисляем должен совпасть с
указанной в п.4 точностью, иначе надо проверить п.5.
7.Вычисляем 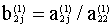 и записываем в четвёртой строке раздела 2
8.Проверка как в п.4.
9.Вычисляем и записываем в четвёртой строке раздела 2
8.Проверка как в п.4.
9.Вычисляем 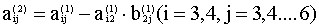 и записываем в первые две строки раздела 3.
10.Проверка как в п.4.
11.Вычисляем и записываем в первые две строки раздела 3.
10.Проверка как в п.4.
11.Вычисляем 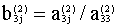 (j=3,4,5,6) и записываем в третьей строке раздела 3.
12.Проверка как в п.4.
13. Вычисляем (j=3,4,5,6) и записываем в третьей строке раздела 3.
12.Проверка как в п.4.
13. Вычисляем 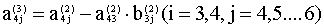 и записываем в первую строку раздела 4. и записываем в первую строку раздела 4.
| i | ai1 | ai2 | ai3 | ai4 | ai5 | åai6 | | 1 | 1 2 3 4 | 9.3 4.92 4.77 3.21 1.0 | 2.42 7.45 7.01 1.85 0.2602 | 6.1 8.9 9.04 3.69 0.6559 | 1.9 2.46 2.28 6.99 0.2043 | -9.05 10.21 13.45 -10.35 -0.9731 | 10.67 33.94 36.55 5.39 1.1473 | | 2 | 2 3 4 | | 6.1698 5.7688 1.0148 1.0 | 5.6730 5.9114 1.5846 0.9195 | 1.4548 1.3055 6.3342 0.2358 | 14.9977 18.0918 -7.2263 2.4308 | 28.2953 31.0775 1.7073 4.5861 | | 3 | 3 4 | | | 0.6069 0.6515 1 | -0.0547 6.0949 -0.0901 | 4.0690 -9.6931 6.7045 | 4.6212 -2.9467 7.6144 | 4 5 | 4 | 1 | 1 | 1 | 6.1536 1 | -14.0611 -2.2850 6,4986 -3.0059 -3.9866 | -7.9075 -1.2850 7,4986 -2.0059 -2.9866 |
Обратный ход:

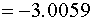
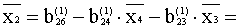 4.5861-0.2358(-1.2850)-0.9195.7.4986=2.0059 4.5861-0.2358(-1.2850)-0.9195.7.4986=2.0059
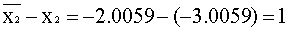 x1=b15-b14.x4-b13.x13-b12.x2=-0.9731-0.2043(-2.2850)-0.6559 . 6.4986-0.2602.
(-3.0059)=-3.9866
x1=b15-b14.x4-b13.x13-b12.x2=-0.9731-0.2043(-2.2850)-0.6559 . 6.4986-0.2602.
(-3.0059)=-3.9866
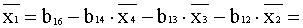 1.1473-0.2043(-1.2850)-0.6559 . 7.4986-
-0.2602 . (-2.0059)=-2.9866 1.1473-0.2043(-1.2850)-0.6559 . 7.4986-
-0.2602 . (-2.0059)=-2.9866
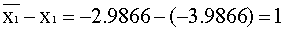 Вывод по решению:
В результате проделанной работы мы решили систему из четырёх уравнений методом
Гаусса и получили: X1=-2.2850; X2= 6.4986; X3
=-3.0059; X4=-3.9866.
4.Задача 4
4.1.Постановка задачи
Дано дифференциальное уравнение :
Вывод по решению:
В результате проделанной работы мы решили систему из четырёх уравнений методом
Гаусса и получили: X1=-2.2850; X2= 6.4986; X3
=-3.0059; X4=-3.9866.
4.Задача 4
4.1.Постановка задачи
Дано дифференциальное уравнение :
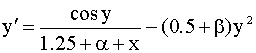 где a=0,5 b=0
Начальное условие y(0)=0
Необходимо найти методом Рунге-Кутта его решение на отрезке [0;0,3]
c шагом h=0.1
4.1.Решение
Дифференциальное уравнение :
где a=0,5 b=0
Начальное условие y(0)=0
Необходимо найти методом Рунге-Кутта его решение на отрезке [0;0,3]
c шагом h=0.1
4.1.Решение
Дифференциальное уравнение :
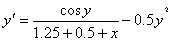 решаем методом Рунге-Кутта по вычислительной схеме приведенной в методическом
указании по выполнению курсовой работы.
Для вычисления воспользуемся таблицей 4.1. включив в неё вычисления правой
части f(x,y).
Наиболее часто используется метод численного интегрирования дифференциальных
уравнений первого порядка.
y'=f(x,y), y(x0)=y
Метод Рунге-Кутта четвёртого порядка.
В этом методе на одном шаге интегрирования при вычислении
yi+1=yi+Dyi
приращение Dyi определяется как сумма четырёх приращений взятых с
различными весовыми коэффициентами :
решаем методом Рунге-Кутта по вычислительной схеме приведенной в методическом
указании по выполнению курсовой работы.
Для вычисления воспользуемся таблицей 4.1. включив в неё вычисления правой
части f(x,y).
Наиболее часто используется метод численного интегрирования дифференциальных
уравнений первого порядка.
y'=f(x,y), y(x0)=y
Метод Рунге-Кутта четвёртого порядка.
В этом методе на одном шаге интегрирования при вычислении
yi+1=yi+Dyi
приращение Dyi определяется как сумма четырёх приращений взятых с
различными весовыми коэффициентами :
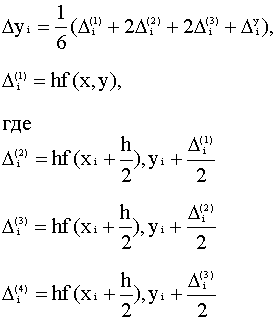 Порядок заполнения таблицы:
1. Записываем в первой строке таблицы данные правой части x0 ,y0
2. Вычисляем f(x0,y0),умножаем на h и заносим в таблицу в качестве D1(0).
3. Записываем во второй строке таблицы
Порядок заполнения таблицы:
1. Записываем в первой строке таблицы данные правой части x0 ,y0
2. Вычисляем f(x0,y0),умножаем на h и заносим в таблицу в качестве D1(0).
3. Записываем во второй строке таблицы 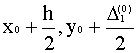 4. Вычисляем
4. Вычисляем 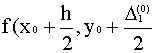 ) умножаем на h и заносим в таблицу в качестве ) умножаем на h и заносим в таблицу в качестве 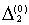 .
5. Записываем в третьей строке таблицы
6. .
5. Записываем в третьей строке таблицы
6. 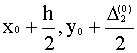 Вычисляем
Вычисляем 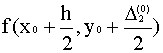 ,умножаем на h и заносим в таблицу в качестве ,умножаем на h и заносим в таблицу в качестве 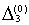 .
7. Записываем в четвёртой строке таблицы .
7. Записываем в четвёртой строке таблицы 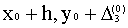 8. Вычисляем
8. Вычисляем 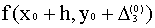 и умножаем на h заносим в таблицу в качестве D4
9. В столбец и умножаем на h заносим в таблицу в качестве D4
9. В столбец 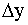 записываем числа записываем числа 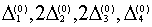 10. Суммируем числа стоящие в столбце
10. Суммируем числа стоящие в столбце 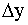 делим на 6 и заносим в таблицу в качестве
делим на 6 и заносим в таблицу в качестве 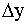 0
Вычисляем y1=y0+
0
Вычисляем y1=y0+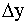 0.затем продолжаем вычисления в том же порядке принимая за начальную точку
(x1,y1)
Таблица 4.1.
0.затем продолжаем вычисления в том же порядке принимая за начальную точку
(x1,y1)
Таблица 4.1.
| i | x | Y | D =hf(x,y) | Dy | | 0 | 0.00000 0.05000 0.05000 0.10000 | 0.00000 0.02857 0.02757 0.05517 | 0.05714 0.05514 0.05517 0.05253 | 0.05714 0.11028 0.11034 0.05253 | | | | | 0.05504 | | 1 | 0.10000 0.15000 0.15000 0.20000 | 0.05504 0.08060 0.07973 0.10445 | 0.05112 0.04938 0.04945 0.04333 | 0.10224 0.09876 0.09890 0.04333 | | | | | 0.05721 | | 2 | 0.20000 0.25000 0.25000 0.30000 | 0.10087 0.12651 0.12187 0.14344 | 0.05128 0.04199 0.04257 0.03849 | 0.10256 0.08399 0.08514 0.03849 | | | | | 0.05169 | | 3 | 0.30000 | 0.15256 | | |
В результате проделанной работы мы нашли решения дифференциального уравнения :
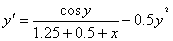 методом Рунге-Кутта и получили следующие решения:
Y(0)=0
Y(0.1)=0.05504
Y(0.2)=0.10087
Y(0.3)=0.15256
СПИСОК ЛИТЕРАТУРЫ
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М:
Наука, 1970.
2. Кувыкина М.И. Методические указания по курсу информатика. – М.: 1996.
3. Фокс Д. Бейсик для всех. – М.: Энергоатомиздат , 1987.
методом Рунге-Кутта и получили следующие решения:
Y(0)=0
Y(0.1)=0.05504
Y(0.2)=0.10087
Y(0.3)=0.15256
СПИСОК ЛИТЕРАТУРЫ
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М:
Наука, 1970.
2. Кувыкина М.И. Методические указания по курсу информатика. – М.: 1996.
3. Фокс Д. Бейсик для всех. – М.: Энергоатомиздат , 1987.
|
|
|
|
|

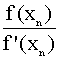 Необходимо выбрать начальное значение x0 , исходя из условия сходимости:
f(x0)f "(x0)>0
f(x)= tg(0.5x+0.2) – x2
Необходимо выбрать начальное значение x0 , исходя из условия сходимости:
f(x0)f "(x0)>0
f(x)= tg(0.5x+0.2) – x2
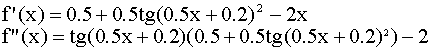 Проверяем условия сходимости для x=0 :
Проверяем условия сходимости для x=0 :
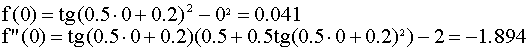 f(0)f"(0)<0,условие не соблюдается
f(0)f"(0)<0,условие не соблюдается 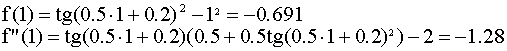 f(0)f"(0)>0,условие соблюдается
берём за x0=1
и условие:
Т=
f(0)f"(0)>0,условие соблюдается
берём за x0=1
и условие:
Т=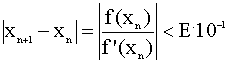 Решение запишем в виде таблицы:
Решение запишем в виде таблицы:
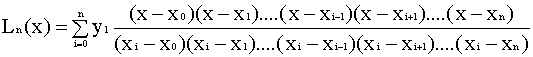 ;
Выражения,называемые коэффициентами Лагранжа:
;
Выражения,называемые коэффициентами Лагранжа:
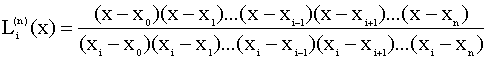 Далее построим матрицу Лагранжа:
Далее построим матрицу Лагранжа:
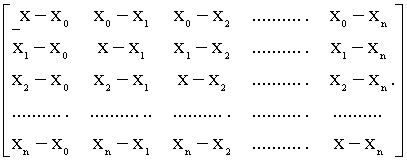 Обозначим произведение строк через
Обозначим произведение строк через 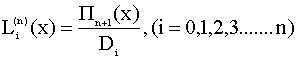
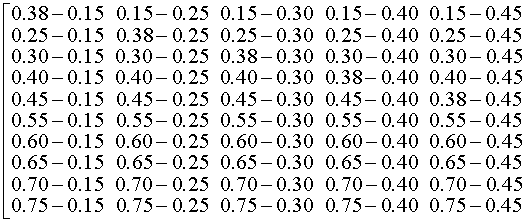
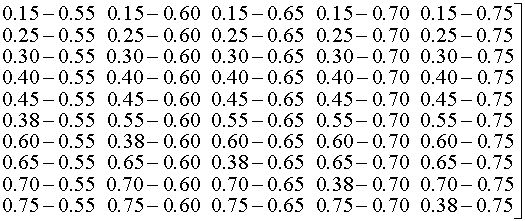 Вычислим её:
Вычислим её:
 отсюда:
Пn+1=4,00384 .10-9
D0=7,68488.10-6 D5=1.1475.10-8
D1=-1.84275.10-7 D6= -1.16944.10-8
D2= 4.2525.10-8 D7=2.3625.10-8
D3=2.92313 10-9 D8= -8.91.10-8
D4= -7.0875.10-9 D9=7.86713.10-7
отсюда:
Пn+1=4,00384 .10-9
D0=7,68488.10-6 D5=1.1475.10-8
D1=-1.84275.10-7 D6= -1.16944.10-8
D2= 4.2525.10-8 D7=2.3625.10-8
D3=2.92313 10-9 D8= -8.91.10-8
D4= -7.0875.10-9 D9=7.86713.10-7
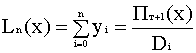 ,
имеем
,
имеем
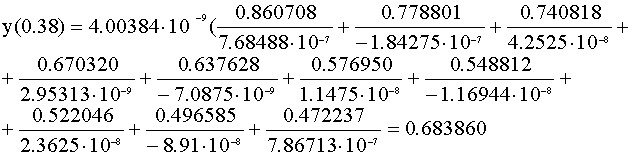 В результате проделанной работы мы произвели интерполяцию функции заданной
таблицей 2.1 и получили значение функции в точке х=0,38 y=0,683860.
О справедливости полученного результата мы можем судить из того ,что точка
х=0,38 находиться точками х=0,30 и х=0,40 и искомое значение должно
находиться между соответствующими значениями этих точек. Полученное значение
y=0,683860 находиться в пределах между y(0.30)=0.670320 и y(0.40)=0.740818.
Следовательно решение верно.
3.Задача 3
3.1.Постановка задачи
В результате проделанной работы мы произвели интерполяцию функции заданной
таблицей 2.1 и получили значение функции в точке х=0,38 y=0,683860.
О справедливости полученного результата мы можем судить из того ,что точка
х=0,38 находиться точками х=0,30 и х=0,40 и искомое значение должно
находиться между соответствующими значениями этих точек. Полученное значение
y=0,683860 находиться в пределах между y(0.30)=0.670320 и y(0.40)=0.740818.
Следовательно решение верно.
3.Задача 3
3.1.Постановка задачи
 или
или а15,а25,а35,а45---свободные члены
а15,а25,а35,а45---свободные члены

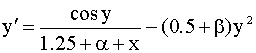 где a=0,5 b=0
Начальное условие y(0)=0
Необходимо найти методом Рунге-Кутта его решение на отрезке [0;0,3]
c шагом h=0.1
4.1.Решение
Дифференциальное уравнение :
где a=0,5 b=0
Начальное условие y(0)=0
Необходимо найти методом Рунге-Кутта его решение на отрезке [0;0,3]
c шагом h=0.1
4.1.Решение
Дифференциальное уравнение :
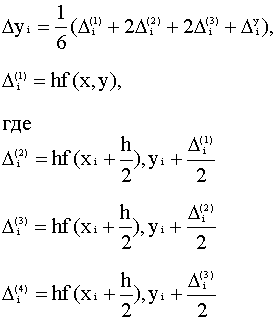 Порядок заполнения таблицы:
1. Записываем в первой строке таблицы данные правой части x0 ,y0
2. Вычисляем f(x0,y0),умножаем на h и заносим в таблицу в качестве D1(0).
3. Записываем во второй строке таблицы
Порядок заполнения таблицы:
1. Записываем в первой строке таблицы данные правой части x0 ,y0
2. Вычисляем f(x0,y0),умножаем на h и заносим в таблицу в качестве D1(0).
3. Записываем во второй строке таблицы 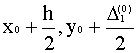 4. Вычисляем
4. Вычисляем 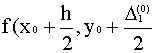 ) умножаем на h и заносим в таблицу в качестве
) умножаем на h и заносим в таблицу в качестве 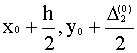 Вычисляем
Вычисляем 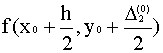 ,умножаем на h и заносим в таблицу в качестве
,умножаем на h и заносим в таблицу в качестве