|
|
|
|
Курсовая: Курсовая работа по численным методам
Курсовая: Курсовая работа по численным методам
1. Методом Крылова развернуть характеристический определитель матрицы А=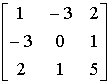 . Исходную систему линейных уравнений решить методом Жордана-Гаусса.
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль
свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем
своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
. Исходную систему линейных уравнений решить методом Жордана-Гаусса.
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль
свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем
своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
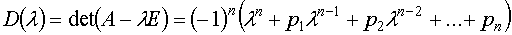 – (1)
характеристический многочлен.
Заменяя в выражении (1) величину
– (1)
характеристический многочлен.
Заменяя в выражении (1) величину 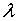 на на 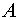 , получим , получим
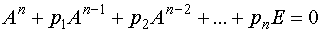 . (2)
Возьмем произвольный ненулевой вектор . (2)
Возьмем произвольный ненулевой вектор
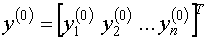 . (3)
Умножим обе части выражения (2) на . (3)
Умножим обе части выражения (2) на 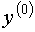 : :
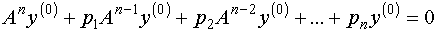 (4)
Положим
(4)
Положим
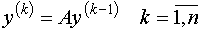 , (5)
т.е. , (5)
т.е.
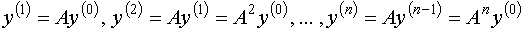 (6)
Учитывая (5), выражение (4) запишем в виде
(6)
Учитывая (5), выражение (4) запишем в виде
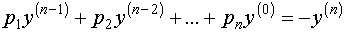 , (7)
или в виде , (7)
или в виде
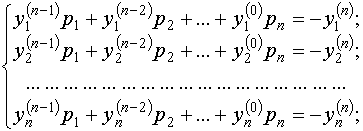 Решаем систему (7). Если эта система имеет единственное решение, то ее корни
Решаем систему (7). Если эта система имеет единственное решение, то ее корни 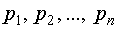 являются коэффициентами характеристического многочлена (1).
Если известны коэффициенты
являются коэффициентами характеристического многочлена (1).
Если известны коэффициенты 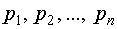 и корни
и корни 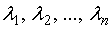 характеристического многочлена, то метод Крылова дает возможность найти
соответствующие собственные векторы по следующей формуле:
характеристического многочлена, то метод Крылова дает возможность найти
соответствующие собственные векторы по следующей формуле:
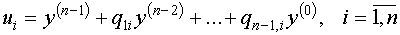 (8)
Здесь (8)
Здесь 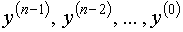 – векторы,
использованные при нахождении коэффициентов – векторы,
использованные при нахождении коэффициентов 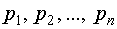 методом Крылова, а коэффициенты
методом Крылова, а коэффициенты 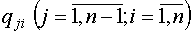 определяются по схеме Горнера
определяются по схеме Горнера
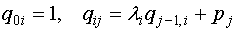 (9)
Используя все выше сказанное, развернем характеристический определитель матрицы
А= (9)
Используя все выше сказанное, развернем характеристический определитель матрицы
А=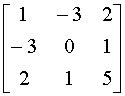 методом Крылова.
Выберем в качестве начального следующий вектор: методом Крылова.
Выберем в качестве начального следующий вектор:
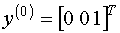 , , 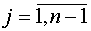 Вычислим
Вычислим
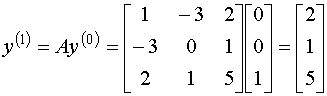 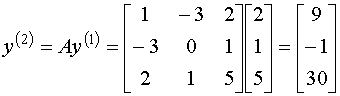 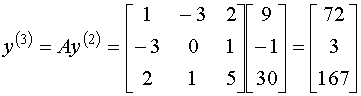 Составим матричное уравнение
Составим матричное уравнение
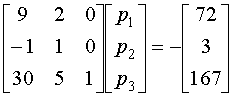 , или , или 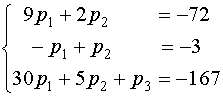 Полученную систему уравнений решим методом Жордана-Гаусса.
Полученную систему уравнений решим методом Жордана-Гаусса.
| 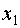
| 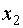
| 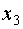
| 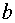
| 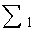
| 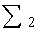
| | 1 | 9 | 2 | 0 | -72 | -61 | -61 | | -1 | 1 | 0 | -3 | -3 | -3 | | 30 | 5 | 1 | -167 | -131 | -131 | | 2 | 1 | 2/9 | 0 | -8 | -61/9 | -61/9 | | 0 | 11/9 | 0 | -11 | -88/9 | -88/9 | | 0 | -15/9 | 1 | 657/9 | 651/9 | 651/9 | | 3 | 1 | 0 | 0 | -6 | -5 | -5 | | 0 | 1 | 0 | -9 | -8 | -8 | | 0 | 0 | 1 | 58 | 59 | 59 | | 4 | 1 | 0 | 0 | | | | | 0 | 1 | 0 | | | | | 0 | 0 | 1 | | | |
Исходя из результатов таблицы, имеем 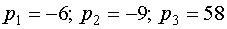 .
Таким образом характеристическое уравнение матрицы .
Таким образом характеристическое уравнение матрицы 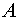 имеет вид имеет вид
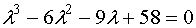 2. Для определения собственных чисел матрицы
2. Для определения собственных чисел матрицы 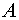 необходимо решить полученное характеристическое уравнение третьей степени
необходимо решить полученное характеристическое уравнение третьей степени
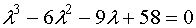 Данное кубическое уравнение невозможно решить стандартными средствами.
Воспользуемся для этой цели числовыми методами, а точнее методами
приближенного вычисления.
2.1 Исследование функции.
Вычислим первую и вторую производные данной функции
Данное кубическое уравнение невозможно решить стандартными средствами.
Воспользуемся для этой цели числовыми методами, а точнее методами
приближенного вычисления.
2.1 Исследование функции.
Вычислим первую и вторую производные данной функции
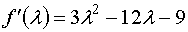
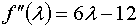 Необходимо выбрать интервал, на котором будем находить решение.
Для отделения корней существует несколько способов. Наиболее популярные из
них – графический и аналитический.
В литературе рассматриваются эти способы по отдельности. По заданию курсовой
работы требуется отделить корни каждым из этих способов. Рискну нарушить это
требование, и объединить эти два способа в один. То есть исследовать функцию
аналитически и по результатам исследования построить приблизительный график
функции.
Областью значений исходного уравнения является вся ось
Необходимо выбрать интервал, на котором будем находить решение.
Для отделения корней существует несколько способов. Наиболее популярные из
них – графический и аналитический.
В литературе рассматриваются эти способы по отдельности. По заданию курсовой
работы требуется отделить корни каждым из этих способов. Рискну нарушить это
требование, и объединить эти два способа в один. То есть исследовать функцию
аналитически и по результатам исследования построить приблизительный график
функции.
Областью значений исходного уравнения является вся ось 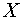 .
Приравняв первую производную к нулю, мы можем получить критические точки
данной функции (точки минимумов и максимумов, или же точки, в которых функция
не определена). .
Приравняв первую производную к нулю, мы можем получить критические точки
данной функции (точки минимумов и максимумов, или же точки, в которых функция
не определена).
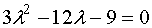
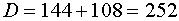
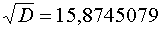 Стоит отметить, что для вычисления квадратного корня, также применимы
числовые методы, на которых и основаны микрокалькуляторы и программы для ЭВМ.
Данные методы основаны на логарифмировании корня и последующего вычисления.
Стоит отметить, что для вычисления квадратного корня, также применимы
числовые методы, на которых и основаны микрокалькуляторы и программы для ЭВМ.
Данные методы основаны на логарифмировании корня и последующего вычисления.
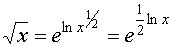
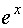 вычисляется при помощи числового ряда вычисляется при помощи числового ряда
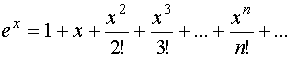 Уравнение
Уравнение 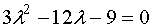 имеет
решение имеет
решение 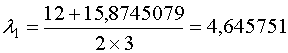 , , 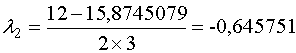 . Изменив знак равенства на знак неравенства (< или >), можем найти
промежутки возрастания и убывания функции.
Функция возрастает на промежутке
. Изменив знак равенства на знак неравенства (< или >), можем найти
промежутки возрастания и убывания функции.
Функция возрастает на промежутке 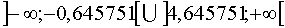 и убывает на промежутке
и убывает на промежутке 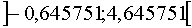 . Подставив в исходное уравнение значения критических точек, имеем в результате
для
. Подставив в исходное уравнение значения критических точек, имеем в результате
для 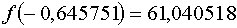 и для и для 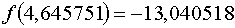 .
Приравняв вторую производную к нулю, мы можем найти точку перегиба и,
соответственно, найти интервал, на котором функция выпуклая и вогнутая.
.
Приравняв вторую производную к нулю, мы можем найти точку перегиба и,
соответственно, найти интервал, на котором функция выпуклая и вогнутая.
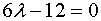
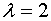
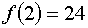 Далее необходимо найти, интервалы, в которых график функции пересекает ось
Далее необходимо найти, интервалы, в которых график функции пересекает ось 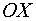 .
Сразу можно определиться, что так при .
Сразу можно определиться, что так при 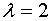 значение функции больше нуля, а при
значение функции больше нуля, а при 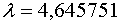 - меньше нуля, то одна из точек пересечения, будет лежать на данном интервале.
Произведя не хитрые математические вычисления значения функции для
- меньше нуля, то одна из точек пересечения, будет лежать на данном интервале.
Произведя не хитрые математические вычисления значения функции для 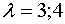 , сузим интервал до
, сузим интервал до 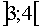 .
Далее рассмотрим оставшиеся два интервала.
Известно, что при
.
Далее рассмотрим оставшиеся два интервала.
Известно, что при 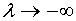 -
значение функции отрицательно, а в первой критической точке положительно, то
будем сужать этот промежуток. В данном случае применим метод половинного
деления. -
значение функции отрицательно, а в первой критической точке положительно, то
будем сужать этот промежуток. В данном случае применим метод половинного
деления.
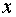
| 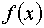
| | 0 | 58 | | -100 | -1059042 | | -50 | -139492 | | -25 | -19092 | | -12 | -2426 | | -6 | -320 | | -3 | 4 | | -5 | -172 | | -4 | -66 |
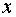
| 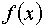
| | 4 | -10 | | 100 | 939158 | | 50 | 109608 | | 25 | 11708 | | 12 | 814 | | 6 | 4 | | 5 | -12 |
Таким образом получили еще один интервал 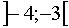 .
Следующий будет от .
Следующий будет от 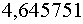 и до бесконечности.
Произведем аналогичные вычисления и получим промежуток и до бесконечности.
Произведем аналогичные вычисления и получим промежуток 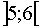 На основании произведенного анализа построим график исходной функции.
На основании произведенного анализа построим график исходной функции.
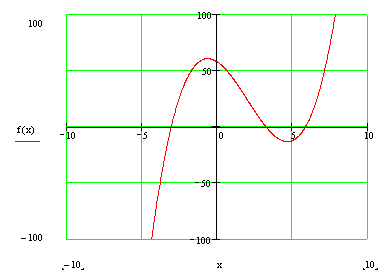 2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении
методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е.
2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении
методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е. 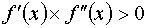 .
В этом случае итерационный процесс осуществляем по формуле
.
В этом случае итерационный процесс осуществляем по формуле
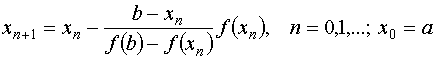 Случай второй. Первая и вторая производные функции имеют разные знаки, т.е.
Случай второй. Первая и вторая производные функции имеют разные знаки, т.е. 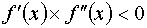 .
В этом случае итерационный процесс осуществляем по формуле .
В этом случае итерационный процесс осуществляем по формуле
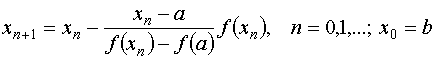 Для оценки точности приближение можно воспользоваться формулой
Для оценки точности приближение можно воспользоваться формулой
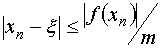 ,
где ,
где 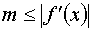 при при 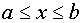 , , 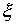 – точное значение корня.
Итак решим наше уравнение – точное значение корня.
Итак решим наше уравнение 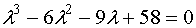 методом хорд с точностью методом хорд с точностью 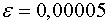 .
2.2.1 Интервал .
2.2.1 Интервал 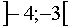 . .
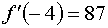
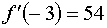
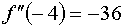
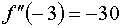
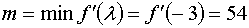 Так как первая и вторые производные в точке, от которой мы начинаем работать
имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
Так как первая и вторые производные в точке, от которой мы начинаем работать
имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
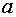
| 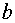
| 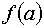
| 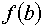
| 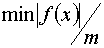
| -4,0000000 | -3,0000000 | -66,0000000 | 4,0000000 | 0,0740741 | -4,0000000 | -3,1142857 | -66,0000000 | -2,3688397 | 0,0438674 | -4,0000000 | -3,0440850 | -66,0000000 | 1,5901736 | 0,0294477 | -4,0000000 | -3,0901012 | -66,0000000 | -0,9879693 | 0,0182957 | -4,0000000 | -3,0610770 | -66,0000000 | 0,6456578 | 0,0119566 | -4,0000000 | -3,0798611 | -66,0000000 | -0,4086778 | 0,0075681 | -4,0000000 | -3,0678974 | -66,0000000 | 0,2640772 | 0,0048903 | -4,0000000 | -3,0755972 | -66,0000000 | -0,1684077 | 0,0031187 | -4,0000000 | -3,0706743 | -66,0000000 | 0,1083107 | 0,0020058 | -4,0000000 | -3,0738353 | -66,0000000 | -0,0692833 | 0,0012830 | -4,0000000 | -3,0718112 | -66,0000000 | 0,0444729 | 0,0008236 | -4,0000000 | -3,0731096 | -66,0000000 | -0,0284836 | 0,0005275 | -4,0000000 | -3,0722776 | -66,0000000 | 0,0182690 | 0,0003383 | -4,0000000 | -3,0728111 | -66,0000000 | -0,0117068 | 0,0002168 | -4,0000000 | -3,0724692 | -66,0000000 | 0,0075061 | 0,0001390 | -4,0000000 | -3,0726884 | -66,0000000 | -0,0048109 | 0,0000891 | -4,0000000 | -3,0725479 | -66,0000000 | 0,0030843 | 0,0000571 | -4,0000000 | -3,0726380 | -66,0000000 | -0,0019770 | 0,0000366 |
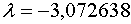 2.2.2 Интервал
2.2.2 Интервал 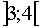 . .
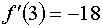
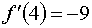
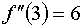
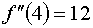
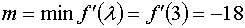 Так как первая и вторые производные в точке, от которой мы начинаем работать
имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
Так как первая и вторые производные в точке, от которой мы начинаем работать
имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
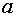
| 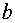
| 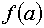
| 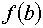
| 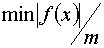
| 3,0000000 | 4,0000000 | 4,0000000 | -10,0000000 | -0,2222222 | 3,0000000 | 3,2857143 | 4,0000000 | -0,8746356 | -0,0485909 | 3,0000000 | 3,2344498 | 4,0000000 | -0,0423087 | -0,0023505 | 3,0000000 | 3,2319959 | 4,0000000 | -0,0019734 | -0,0001096 | 3,0000000 | 3,2318815 | 4,0000000 | -0,0000919 | -0,0000051 |
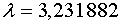 2.2.3 Интервал
2.2.3 Интервал 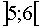 . .
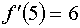
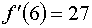
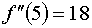
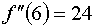
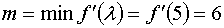 Так как первая и вторые производные в точке, от которой мы начинаем работать
имеют одинаковые знаки, то работаем по первому варианту.
Результаты вычисления приведены в таблице.
Так как первая и вторые производные в точке, от которой мы начинаем работать
имеют одинаковые знаки, то работаем по первому варианту.
Результаты вычисления приведены в таблице.
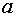
| 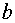
| 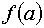
| 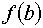
| 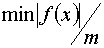
| 5,0000000 | 6,0000000 | -12,0000000 | 4,0000000 | 0,6666667 | 5,7500000 | 6,0000000 | -2,0156250 | 4,0000000 | 0,3359375 | 5,8337662 | 6,0000000 | -0,1613014 | 4,0000000 | 0,0268836 | 5,8402098 | 6,0000000 | -0,0120198 | 4,0000000 | 0,0020033 | 5,8406885 | 6,0000000 | -0,0008909 | 4,0000000 | 0,0001485 | 5,8407240 | 6,0000000 | -0,0000660 | 4,0000000 | 0,0000110 |
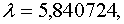 Итак, корнями уравнения
Итак, корнями уравнения 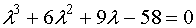 будут будут 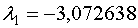 , , 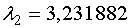 , , 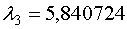 .
2.3 Метод касательных (метод Ньютона).
В век повальной компьютеризации не есть хорошо считать при помощи
логарифмической линейки. Поэтому, разработаем алгоритм и прикладную программу
для решения кубических уравнений методом Ньютона.
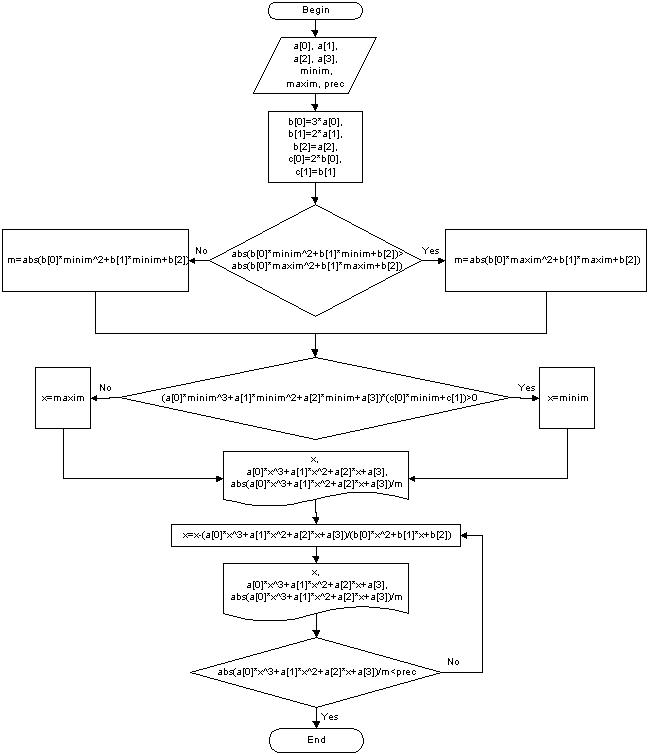
Ниже приведена блок-схема алгоритма и листинг программы, реализующей данный
алгоритм на языке С++. Также привожу текст, которая выдает данная программа
при решении исходного уравнения. .
2.3 Метод касательных (метод Ньютона).
В век повальной компьютеризации не есть хорошо считать при помощи
логарифмической линейки. Поэтому, разработаем алгоритм и прикладную программу
для решения кубических уравнений методом Ньютона.
Ниже приведена блок-схема алгоритма и листинг программы, реализующей данный
алгоритм на языке С++. Также привожу текст, которая выдает данная программа
при решении исходного уравнения.
 //метод Ньютона длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом касательных
(метод Ньютона).\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"\n\n\n"
<<"Исходное уравнение имеет вид : \n\n"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0\n\n"
<<"ПерваЯ производнаЯ имеет вид : \n\n"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")\n\n"
<<"ВтораЯ производнаЯ имеет вид : \n\n"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")\n\n";
}
void Calculation()
<<"-------------------------------------------------"<<endl;
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
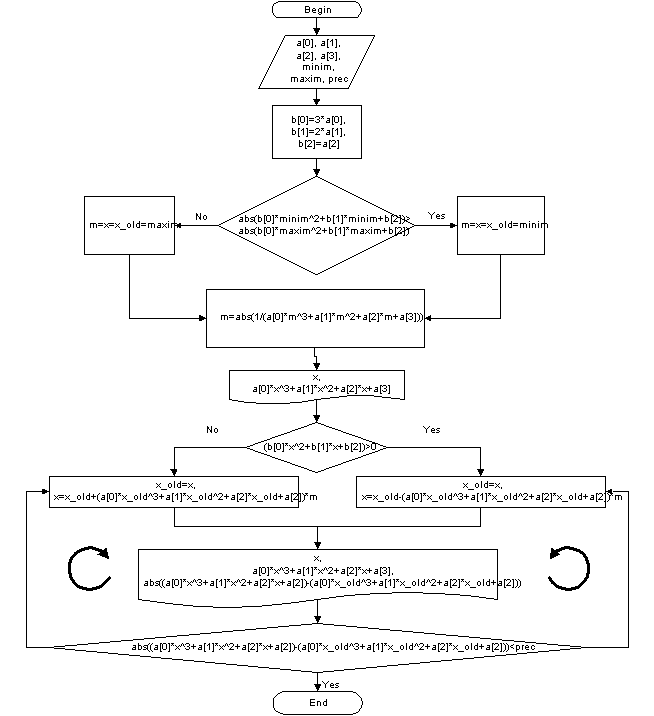
2.4 Метод итераций. Как и для предыдущего метода, привожу блок-схему
алгоритма решения и листинг программы, реализующей этот алгоритм на языке
программирования С++.
//метод Ньютона длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом касательных
(метод Ньютона).\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"\n\n\n"
<<"Исходное уравнение имеет вид : \n\n"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0\n\n"
<<"ПерваЯ производнаЯ имеет вид : \n\n"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")\n\n"
<<"ВтораЯ производнаЯ имеет вид : \n\n"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")\n\n";
}
void Calculation()
<<"-------------------------------------------------"<<endl;
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
2.4 Метод итераций. Как и для предыдущего метода, привожу блок-схему
алгоритма решения и листинг программы, реализующей этот алгоритм на языке
программирования С++.
 //метод итераций длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом итераций.\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |\n";
if(Calc_First(x)>0)
{
do
cout.width(15);cout.precision(10);
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
cout<<"
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
Решив уравнение
//метод итераций длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом итераций.\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |\n";
if(Calc_First(x)>0)
{
do
cout.width(15);cout.precision(10);
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
cout<<"
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
Решив уравнение 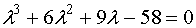 , получили корень , получили корень 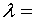
| Метод | Корень № 1 | Корень № 2 | Корень № 3 | | Хорд | -3,072638 | 3,231881 | 5,840724 | | Касательных (Ньютона) | -3,072616 | 3,231855 | 5,840726 | | Итераций | -3,072602 | 3,231875 | 5,840726 |
Для дальнейших расчетов будем использовать среднее арифметическое значение
полученных корней.
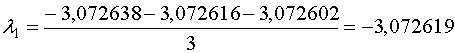
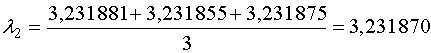
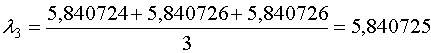 3. Используя полученные значения, определим собственные значения исходной
матрицы.
Собственные вектора матрицы А=
3. Используя полученные значения, определим собственные значения исходной
матрицы.
Собственные вектора матрицы А=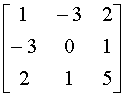 определим по формуле определим по формуле
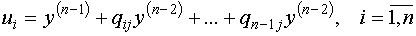 Для нашей матрицы, данная формула примет следующий вид
Для нашей матрицы, данная формула примет следующий вид
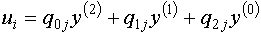 Коэффициенты
Коэффициенты 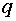 определяются по схеме Горнера: определяются по схеме Горнера:
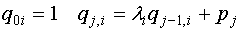 Для
Для 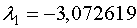 имеем: имеем:
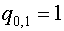
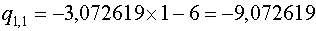
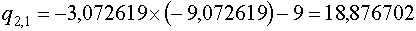 Для
Для 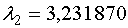 имеем: имеем:
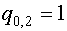
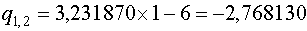
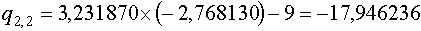 Для
Для 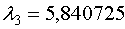 имеем: имеем:
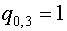
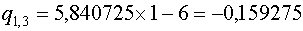
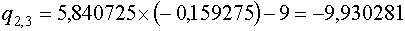 Далее можем найти собственные векторы:
Далее можем найти собственные векторы:
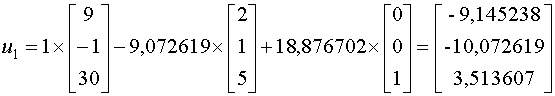
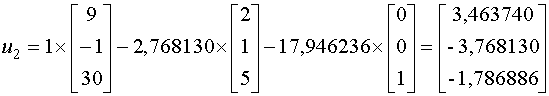
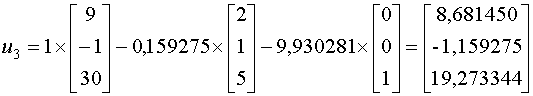 4. Для контроля полученных значений, развернем исходную матрицу А=
4. Для контроля полученных значений, развернем исходную матрицу А=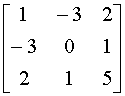 , и определим ее собственные векторы методом непосредственного развертывания.
Характеристический многочлен для данной матрицы имеет вид:
, и определим ее собственные векторы методом непосредственного развертывания.
Характеристический многочлен для данной матрицы имеет вид:
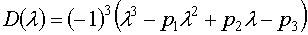 .
Находим .
Находим 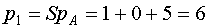 .
Число диагональных миноров второго порядка у матрицы второго порядка .
Число диагональных миноров второго порядка у матрицы второго порядка 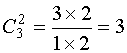 .
Выписываем эти миноры и складываем их: .
Выписываем эти миноры и складываем их:
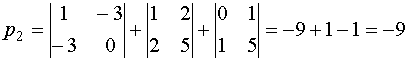 .
И, в заключение, находим
.
И, в заключение, находим
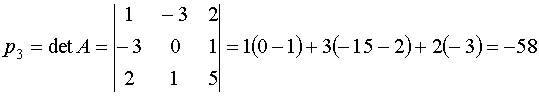 Таким образом, характеристическое уравнение имеет вид
Таким образом, характеристическое уравнение имеет вид
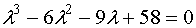 Данное уравнение идентично уравнению, полученному при помощи метода Крылова.
Нет смысла заново его решать. Воспользуемся уже вычисленными корнями (их
средним значением).
Определим собственный вектор
Данное уравнение идентично уравнению, полученному при помощи метода Крылова.
Нет смысла заново его решать. Воспользуемся уже вычисленными корнями (их
средним значением).
Определим собственный вектор 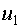 , соответствующий , соответствующий 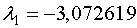 . .
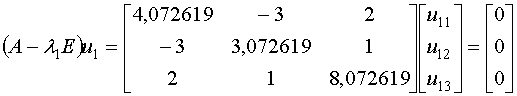 , или
, или
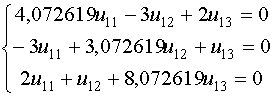 Из третьего уравнения системы выведем
Из третьего уравнения системы выведем 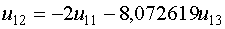 и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
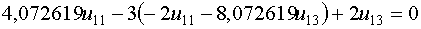
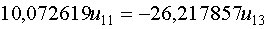 Примем
Примем 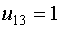 , тогда , тогда 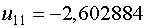 и и 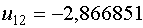 .
Итак, искомый вектор матрицы .
Итак, искомый вектор матрицы 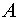 , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя 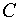 , для собственного значения матрицы
, для собственного значения матрицы 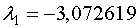 будет:
будет:
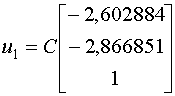 При помощи метода Крылова, мы получили точное значение собственного вектора
При помощи метода Крылова, мы получили точное значение собственного вектора 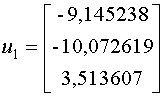 .
Мы можем проверить наши вычисления, взяв .
Мы можем проверить наши вычисления, взяв 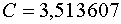 : :
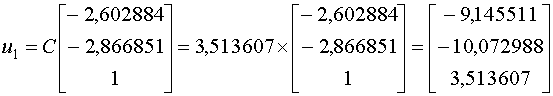 Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор 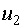 , соответствующий , соответствующий 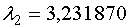 . .
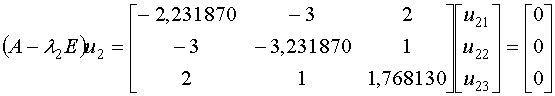 , или
, или
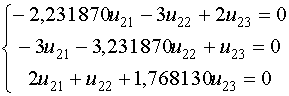 Из третьего уравнения системы выведем
Из третьего уравнения системы выведем 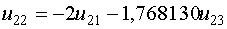 и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
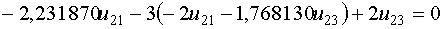
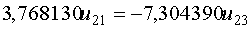 Примем
Примем 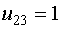 , тогда , тогда 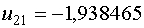 и и 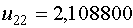 .
Итак, искомый вектор матрицы .
Итак, искомый вектор матрицы 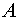 , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя 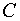 , для собственного значения матрицы
, для собственного значения матрицы 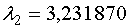 будет:
будет:
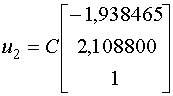 При помощи метода Крылова, мы получили точное значение собственного вектора
При помощи метода Крылова, мы получили точное значение собственного вектора 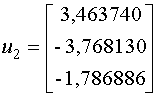 .
Мы можем проверить наши вычисления, взяв .
Мы можем проверить наши вычисления, взяв 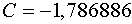 : :
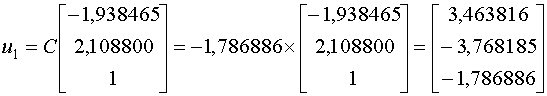 Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор 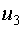 , соответствующий , соответствующий 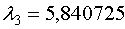 . .
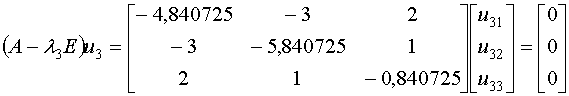 , или
, или
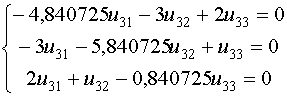 Из третьего уравнения системы выведем
Из третьего уравнения системы выведем 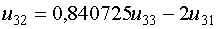 и подставим его в первое уравнение системы
и подставим его в первое уравнение системы
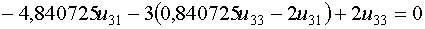
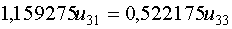 Примем
Примем 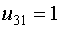 , тогда , тогда 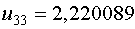 и и 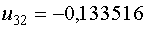 .
Итак, искомый вектор матрицы .
Итак, искомый вектор матрицы 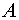 , найденный с точностью до постоянного множителя
, найденный с точностью до постоянного множителя 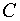 , для собственного значения матрицы
, для собственного значения матрицы 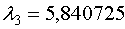 будет:
будет:
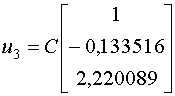 При помощи метода Крылова, мы получили точное значение собственного вектора
При помощи метода Крылова, мы получили точное значение собственного вектора 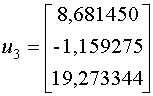 .
Мы можем проверить наши вычисления, взяв .
Мы можем проверить наши вычисления, взяв 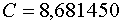 : :
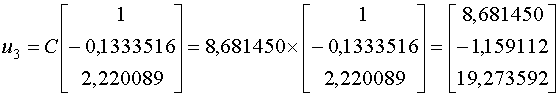 Как видно, мы получил идентичный, до третьего знака, результат.
Как видно, мы получил идентичный, до третьего знака, результат.
|
|
|
|
|

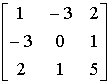 . Исходную систему линейных уравнений решить методом Жордана-Гаусса.
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль
свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем
своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
. Исходную систему линейных уравнений решить методом Жордана-Гаусса.
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль
свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем
своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
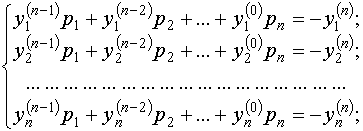 Решаем систему (7). Если эта система имеет единственное решение, то ее корни
Решаем систему (7). Если эта система имеет единственное решение, то ее корни 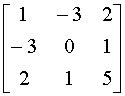 методом Крылова.
Выберем в качестве начального следующий вектор:
методом Крылова.
Выберем в качестве начального следующий вектор:
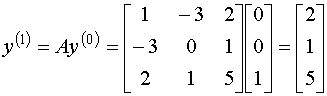
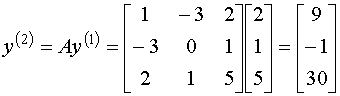
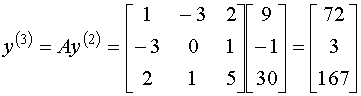 Составим матричное уравнение
Составим матричное уравнение
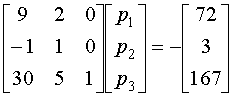 , или
, или 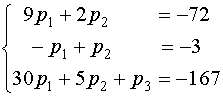 Полученную систему уравнений решим методом Жордана-Гаусса.
Полученную систему уравнений решим методом Жордана-Гаусса.
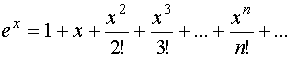 Уравнение
Уравнение 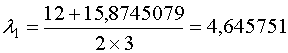 ,
, 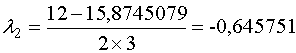 . Изменив знак равенства на знак неравенства (< или >), можем найти
промежутки возрастания и убывания функции.
Функция возрастает на промежутке
. Изменив знак равенства на знак неравенства (< или >), можем найти
промежутки возрастания и убывания функции.
Функция возрастает на промежутке  2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении
методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е.
2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении
методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е. 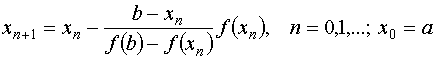 Случай второй. Первая и вторая производные функции имеют разные знаки, т.е.
Случай второй. Первая и вторая производные функции имеют разные знаки, т.е. 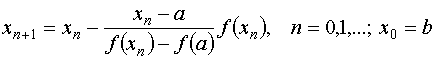 Для оценки точности приближение можно воспользоваться формулой
Для оценки точности приближение можно воспользоваться формулой
 //метод Ньютона длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом касательных
(метод Ньютона).\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"\n\n\n"
<<"Исходное уравнение имеет вид : \n\n"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0\n\n"
<<"ПерваЯ производнаЯ имеет вид : \n\n"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")\n\n"
<<"ВтораЯ производнаЯ имеет вид : \n\n"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")\n\n";
}
void Calculation()
<<"-------------------------------------------------"<<endl;
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
2.4 Метод итераций. Как и для предыдущего метода, привожу блок-схему
алгоритма решения и листинг программы, реализующей этот алгоритм на языке
программирования С++.
//метод Ньютона длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом касательных
(метод Ньютона).\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"\n\n\n"
<<"Исходное уравнение имеет вид : \n\n"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0\n\n"
<<"ПерваЯ производнаЯ имеет вид : \n\n"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")\n\n"
<<"ВтораЯ производнаЯ имеет вид : \n\n"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")\n\n";
}
void Calculation()
<<"-------------------------------------------------"<<endl;
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
ПерваЯ производнаЯ имеет вид :
f'(x)=3x^2+(-12)x+(-9)
ВтораЯ производнаЯ имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
2.4 Метод итераций. Как и для предыдущего метода, привожу блок-схему
алгоритма решения и листинг программы, реализующей этот алгоритм на языке
программирования С++.
 //метод итераций длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом итераций.\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |\n";
if(Calc_First(x)>0)
{
do
cout.width(15);cout.precision(10);
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
cout<<"
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
Решив уравнение
//метод итераций длЯ решениЯ кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа длЯ решениЯ кубических уравнений методом итераций.\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решениЯ."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижнЯЯ граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |\n";
if(Calc_First(x)>0)
{
do
cout.width(15);cout.precision(10);
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
cout<<"
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
Программа длЯ решениЯ кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решениЯ.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
Решив уравнение 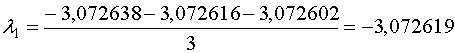
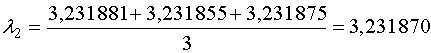
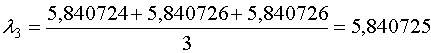 3. Используя полученные значения, определим собственные значения исходной
матрицы.
Собственные вектора матрицы А=
3. Используя полученные значения, определим собственные значения исходной
матрицы.
Собственные вектора матрицы А=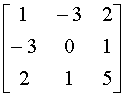 определим по формуле
определим по формуле
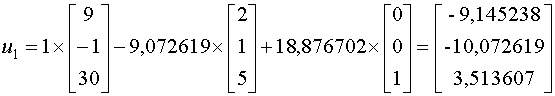
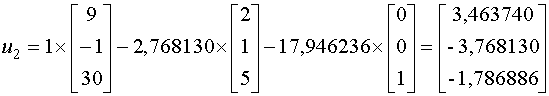
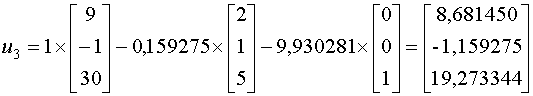 4. Для контроля полученных значений, развернем исходную матрицу А=
4. Для контроля полученных значений, развернем исходную матрицу А=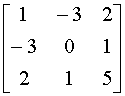 , и определим ее собственные векторы методом непосредственного развертывания.
Характеристический многочлен для данной матрицы имеет вид:
, и определим ее собственные векторы методом непосредственного развертывания.
Характеристический многочлен для данной матрицы имеет вид:
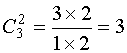 .
Выписываем эти миноры и складываем их:
.
Выписываем эти миноры и складываем их:
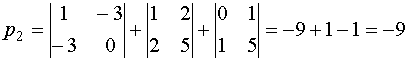 .
И, в заключение, находим
.
И, в заключение, находим
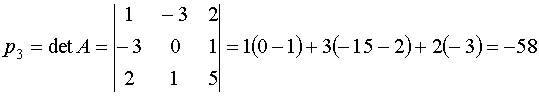 Таким образом, характеристическое уравнение имеет вид
Таким образом, характеристическое уравнение имеет вид
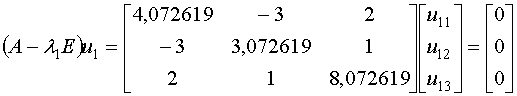 , или
, или
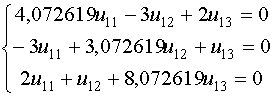 Из третьего уравнения системы выведем
Из третьего уравнения системы выведем 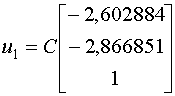 При помощи метода Крылова, мы получили точное значение собственного вектора
При помощи метода Крылова, мы получили точное значение собственного вектора 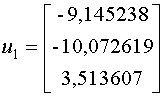 .
Мы можем проверить наши вычисления, взяв
.
Мы можем проверить наши вычисления, взяв 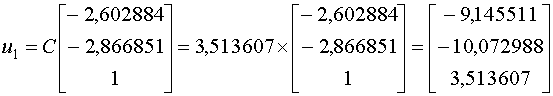 Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор 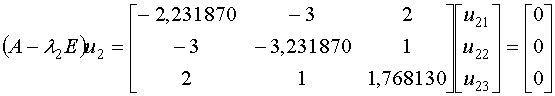 , или
, или
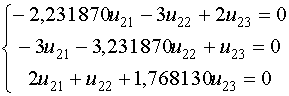 Из третьего уравнения системы выведем
Из третьего уравнения системы выведем 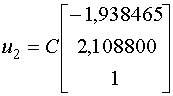 При помощи метода Крылова, мы получили точное значение собственного вектора
При помощи метода Крылова, мы получили точное значение собственного вектора 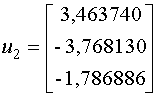 .
Мы можем проверить наши вычисления, взяв
.
Мы можем проверить наши вычисления, взяв 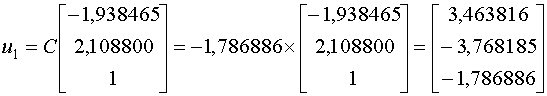 Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор
Как видно, мы получил идентичный, до третьего знака, результат.
Определим собственный вектор 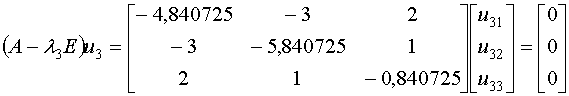 , или
, или
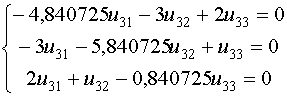 Из третьего уравнения системы выведем
Из третьего уравнения системы выведем 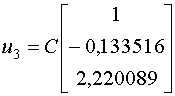 При помощи метода Крылова, мы получили точное значение собственного вектора
При помощи метода Крылова, мы получили точное значение собственного вектора 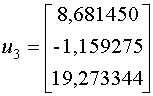 .
Мы можем проверить наши вычисления, взяв
.
Мы можем проверить наши вычисления, взяв 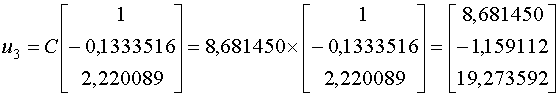 Как видно, мы получил идентичный, до третьего знака, результат.
Как видно, мы получил идентичный, до третьего знака, результат.
