|
|
|
|
Курсовая: Нахождение всех комбинаций расстановки n ферзей на доске n X n
Курсовая: Нахождение всех комбинаций расстановки n ферзей на доске n X n
Государственный комитет Российской Федерации
по высшему и среднеспециальному образованию
Красноярский Государственный Технический Университет
Курсовая работа
по курсу
Математическая логика и теория алгоритмов
Выполнил студент гр. ВТ27-4
Попов А.В.
Проверила:
Пестунова Т.М.
1998
Содержание.
1. Постановка задачи (стр.3).
2. Построение модели (стр.3).
3. Описание алгоритма (стр.4).
4. Доказательство правильности алгоритма (стр.7).
5. Блок-схема алгоритма (стр.8).
6. Описание переменных и программа (стр.9).
7. Расчёт вычислительной сложности (стр.11).
8. Тестирование (стр.11).
9. Список литературы (стр.12).
Постановка задачи.
Перечислить все способы расстановки n ферзей на шахматной доске n на n, при
которых они не бьют друг друга.
Построение модели.
Очевидно, на каждой из n горизонталей должно стоять по ферзю. Будем
называть k-позицией (для k = 0, 1,...,n) произвольную расстановку k ферзей на
k нижних горизонталях (ферзи могут бить друг друга). Нарисуем "дерево
позиций": его корнем будет единственная 0-позиция, а из каждой k-позиции
выходит n стрелок вверх в (k+1)-позиции. Эти n позиций отличаются
положением ферзя на (k+1)-ой горизонтали. Будем считать, что расположение их
на рисунке соответствует положению этого ферзя: левее та позиция, в которой
ферзь расположен левее.
Дерево позиций для n = 2
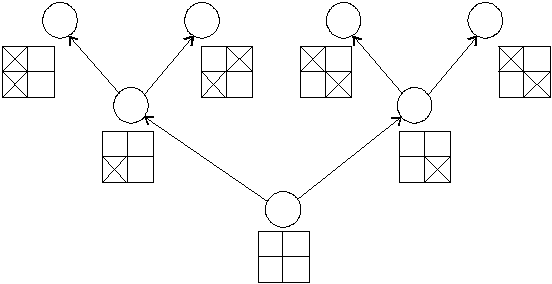Данное дерево представлено только для наглядности и простоты представления
для n=2.
Среди позиций этого дерева нам надо отобрать те n-позиции, в которых ферзи не
бьют друг друга. Программа будет "обходить дерево" и искать их. Чтобы не
делать лишней работы, заметим вот что: если в какой-то k-позиции ферзи бьют
друг друга, то ставить дальнейших ферзей смысла нет. Поэтому, обнаружив это,
мы будем прекращать построение дерева в этом направлении.
Точнее, назовем k-позицию допустимой, если после удаления верхнего ферзя
оставшиеся не бьют друг друга. Наша программа будет рассматривать только
допустимые позиции.
Описание алгоритма.
Разобьем задачу на две части: (1) обход произвольного дерева и (2) реализацию
дерева допустимых позиций.
Сформулируем задачу обхода произвольного дерева. Будем считать, что у нас
имеется Робот, который в каждый момент находится в одной из вершин дерева. Он
умеет выполнять команды:
вверх_налево (идти по самой левой из выходящих вверх стрелок)
вправо (перейти в соседнюю справа вершину)
вниз (спуститься вниз на один уровень)
вверх_налево
вправо
вниз
и проверки, соответствующие возможности выполнить каждую из команд,
называемые "есть_сверху", "есть_справа", "есть_снизу" (последняя истинна
всюду, кроме корня). Обратите внимание, что команда "вправо" позволяет
перейти лишь к "родному брату", но не к "двоюродному".
Будем считать, что у Робота есть команда "обработать" и что его задача -
обработать все листья (вершины, из которых нет стрелок вверх, то есть где
условие "есть_сверху" ложно). Для нашей шахматной задачи команде обработать
будет соответствовать проверка и печать позиции ферзей.
Доказательство правильности приводимой далее программы использует такие
определения. Пусть фиксировано положение Робота в одной из вершин дерева.
Тогда все листья дерева разбиваются на три категории: над Роботом, левее
Робота и правее Робота. (Путь из корня в лист может проходить через вершину с
Роботом, сворачивать влево, не доходя до нее и сворачивать вправо, не доходя
до нее.) Через (ОЛ) обозначим условие "обработаны все листья левее Робота", а
через (ОЛН) - условие "обработаны все листья левее и над Роботом".
Нам понадобится такая процедура:
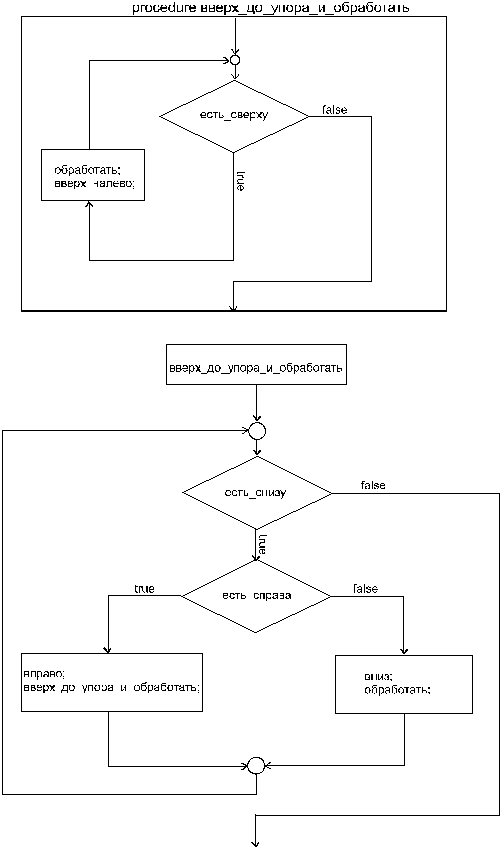
procedure вверх_до_упора_и_обработать
{дано: (ОЛ), надо: (ОЛН)}
begin
{инвариант: ОЛ}
while есть_сверху do begin
вверх_налево
end
{ОЛ, Робот в листе}
обработать;
{ОЛН}
end;
Основной алгоритм:
дано: Робот в корне, листья не обработаны
надо: Робот в корне, листья обработаны
{ОЛ}
вверх_до_упора_и_обработать
{инвариант: ОЛН}
while есть_снизу do begin
if есть_справа then begin {ОЛН, есть справа}
вправо;
{ОЛ}
вверх_до_упора_и_обработать;
end else begin
{ОЛН, не есть_справа, есть_снизу}
вниз;
end;
end;
{ОЛН, Робот в корне => все листья обработаны}
Осталось воспользоваться следующими свойствами команд Робота (сверху записаны
условия, в которых выполняется команда, снизу - утверждения о результате ее
выполнения):
(1) {ОЛ, не есть_сверху} обработать {ОЛН}
(2) {ОЛ} вверх_налево {ОЛ}
(3) {есть_справа, ОЛН} вправо {ОЛ}
(4) {не есть_справа, ОЛН} вниз{ОЛН}
Теперь решим задачу об обходе дерева, если мы хотим, чтобы обрабатывались все
вершины (не только листья).
Решение. Пусть x - некоторая вершина. Тогда любая вершина y относится к
одной из четырех категорий. Рассмотрим путь из корня в y. Он может:
а) быть частью пути из корня в x (y ниже x);
б) свернуть налево с пути в x (y левее x);
в) пройти через x (y над x);
г) свернуть направо с пути в x (y правее x);
В частности, сама вершина x относится к категории в). Условия теперь будут
такими:
(ОНЛ) обработаны все вершины ниже и левее;
(ОНЛН) обработаны все вершины ниже, левее и над.
Вот как будет выглядеть программа:
procedure вверх_до_упора_и_обработать
{дано: (ОНЛ), надо: (ОНЛН)}
begin
{инвариант: ОНЛ}
while есть_сверху do begin
обработать
вверх_налево
end
{ОНЛ, Робот в листе}
обработать;
{ОНЛН}
end;
Основной алгоритм:
дано: Робот в корне, ничего не обработано
надо: Робот в корне, все вершины обработаны
{ОНЛ}
вверх_до_упора_и_обработать
{инвариант: ОНЛН}
while есть_снизу do begin
if есть_справа then begin {ОНЛН, есть справа}
вправо;
{ОНЛ}
вверх_до_упора_и_обработать;
end else begin
{ОЛН, не есть_справа, есть_снизу}
вниз;
end;
end;
{ОНЛН, Робот в корне => все вершины обработаны}
Приведенная только что программа обрабатывает вершину до того, как обработан
любой из ее потомков. Теперь изменим ее, чтобы каждая вершина, не являющаяся
листом, обрабатывалась дважды: один раз до, а другой раз после всех своих
потомков. Листья по-прежнему обрабатываются по разу:
Под "обработано ниже и левее" будем понимать "ниже обработано по разу, слева
обработано полностью (листья по разу, остальные по два)". Под "обработано
ниже, левее и над" будем понимать "ниже обработано по разу, левее и над -
полностью".
Программа будет такой:
procedure вверх_до_упора_и_обработать
{дано: (ОНЛ), надо: (ОНЛН)}
begin
{инвариант: ОНЛ}
while есть_сверху do begin
обработать
вверх_налево
end
{ОНЛ, Робот в листе}
обработать;
{ОНЛН}
end;
Основной алгоритм:
дано: Робот в корне, ничего не обработано
надо: Робот в корне, все вершины обработаны
{ОНЛ}
вверх_до_упора_и_обработать
{инвариант: ОНЛН}
while есть_снизу do begin
if есть_справа then begin {ОНЛН, есть справа}
вправо;
{ОНЛ}
вверх_до_упора_и_обработать;
end else begin
{ОЛН, не есть_справа, есть_снизу}
вниз;
обработать;
end;
end;
{ОНЛН, Робот в корне => все вершины обработаны полностью}
Доказательство правильности алгоритма.
Докажем, что приведенная программа завершает работу (на любом конечном дереве).
Доказательство. Процедура вверх_налево завершает работу (высота
Робота не может увеличиваться бесконечно). Если программа работает бесконечно,
то, поскольку листья не обрабатываются повторно, начиная с некоторого момента
ни один лист не обрабатывается. А это возможно, только если Робот все время
спускается вниз. Противоречие.
Блок-схема алгоритма.
Описание переменных и программа.
Теперь реализуем операции с деревом позиций. Позицию будем представлять с
помощью переменной k: 0..n (число ферзей) и массива c: array [1..n] of 1..n (c
[i] - координаты ферзя на i-ой горизонтали; при i > k значение c [i] роли не
играет). Предполагается, что все позиции допустимы (если убрать верхнего ферзя,
остальные не бьют друг друга).
program queens;
const n = ...;
var k: 0..n;
c: array [1..n] of 1..n;
procedure begin_work; {начать работу}
begin
k := 0;
end;
function danger: boolean; {верхний ферзь под боем}
var b: boolean;
i: integer;
begin
if k <= 1 then begin
danger := false;
end else begin
b := false; i := 1;
{b <=> верхний ферзь под боем ферзей с номерами < i}
while i <> k do begin
b := b or (c[i]=c[k]) {вертикаль}
or (abs(c[i]-c[k])=abs(i-k)); {диагональ}
i := i+ 1;
end;
danger := b;
end;
end;
function is_up: boolean {есть_сверху}
begin
is_up := (k < n) and not danger;
end;
function is_right: boolean {есть_справа}
begin
is_right := (k > 0) and (c[k] < n);
end;
{возможна ошибка: при k=0 не определено c[k]}
function is_down: boolean {есть_снизу}
begin
is_up := (k > 0);
end;
procedure up; {вверх_налево}
begin {k < n}
k := k + 1;
c [k] := 1;
end;
procedure right; {вправо}
begin {k > 0, c[k] < n}
c [k] := c [k] + 1;
end;
procedure down; {вниз}
begin {k > 0}
k := k - 1;
end;
procedure work; {обработать}
var i: integer;
begin
if (k = n) and not danger then begin
for i := 1 to n do begin
write ('<', i, ',' , c[i], '> ');
end;
writeln;
end;
end;
procedure UW; {вверх_до_упора_и_обработать}
begin
while is_up do begin
up;
end
work;
end;
begin
begin_work;
UW;
while is_down do begin
if is_right then begin
right;
UW;
end else begin
down;
end;
end;
end.
Расчёт вычислительной сложности.
Емкостная сложность:
В программе используется одномерный массив размерности n, поэтому объём входа
и объём выхода совпадают и равны n. Количество пременных равно 3(i,b,k) +
1(const n), т.е. объём промежуточных данных равен 4.
С(n)=n+4
Временная сложность:
Если рассматривать обработку каждого листа, без проверки на пути к нему, то
временная сложность T(n) = n0+n1+n2+n3
+.+nn . Но в случае, когда каждая вершина проверяется,
временная сложность T(n) = o(n0+n1+n2+n3
+.+nn). И это тем вернее, чем больше n. Данный вывод получен на
основе приведённых ниже статистических данных:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | | Общее кол-во листьев | 2 | 7 | 40 | 341 | 3906 | 55987 | 960800 | | Кол-во вершин построенного дерева. | 2 | 3 | 4 | 17 | 54 | 153 | 552 | | Время построения(сек) | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| 8 | 9 | 10 | 11 | 12 | 13 | | Общее кол-во листьев |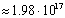 
| 
| 
| 
| 
| 
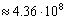
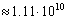
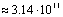
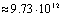
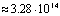
| | Кол-во вершин построенного дерева. | 2057 | 8394 | 35539 | 166926 | 856189 | 4674890 | | Время построения(сек) | <0.01 | 0.21 | 1.20 | 6.48 | 37.12 | 231.29 |
Тестирование.
Построенная по описанному алгоритму программа при различных n выдаёт
следующие данные:
n=4
<1,2><2,4><3,1><4,3>
<1,3><2,1><3,4><4,2>
Т.е. количество расстановок равно 2. Ниже приведена таблица зависимости от n
количества решений (R).
| n = | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | | R= | 1 | 0 | 0 | 2 | 10 | 4 | 40 | 92 | 352 | 724 | 2680 | 14200 | 73712 |
Cписок литературы.
1) Кузнецов О.П. Адельсон-Вельский Г.М. Дискретная математика для
инженера. – М.: Энергоатомиздат, 1988.
2) Евстигнеев В.А. Применение теории графов в программировании. –
М.:Наука, 1984.
3) Основной алгоритм находился на BBS “Master of Univercity” в файле
shen.rar в файловой области “Bardak” (тел. 43-27-03; время работы 21.00 –
7.00; FTN адрес – 2:5090/58).
|
|
|
|
|
