 |
РУБРИКИ |
Курсовая: Неравенство Коши |
РЕКОМЕНДУЕМ |
||
|
Курсовая: Неравенство КошиКурсовая: Неравенство КошиМИНИСТЕРСТВО ПОЛНОГО–ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ кафедра математического анализа Курсовая работа на тему: Неравенства Коши Выполнил: студент 31 гр., ФМФ, Шакиров Айрат Альбиртович Проверил: доц. Каримов Загир Шакирович Уфа – 2002 Оглавление: 1. Введение 2. Множества в Евклидовом пространстве Основные метрические понятия а) Угол между векторами б) Неравенство треугольника 3. Комплексные пространства со скалярным произведением Скалярное произведение (Основные метрические понятия) а) Неравенство Коши–Буняковского б) Неравенство треугольника Введение Коши Огюстен Луи (1789—1857) — знаменитый французский математик. Доказал ряд замечательных теорем в области анализа, теории функций комплексного переменного, теории дифференциальных уравнений и т. д. Большая заслуга Коши — разработка курса анализа, в котором, в частности, он предложил ставшие классическими определения предела, непрерывности функции и т. п. Решительный шаг к созданию прочного фундамента анализа был сделан в 20-е годы прошлого века французским математиком О. Коши (1789—1857), предложившим точные определения пределов функции и последовательности и на их основе доказавшим многие фундаментальные теоремы анализа. Несколько раньше (1821 г.) определения предела и непрерывности, целый ряд других замечательных результатов (в том числе знаменитый пример функции, непрерывной на промежутке, но не имеющей производной ни в одной его точке) получил чешский математик Б. Больцано (1781 —1848), но его работы стали известны много позднее. Определение предела функции по Коши формулируется так: «Число А называется пределом функции f (х) при х, стремящемся к а (т.е. если для любого числа можно подобрать такое число >0, что всех х, удовлетворяющих неравенству 0< | x—а |< ». Опираясь на это определение, уже нетрудно дать определение непрерывности в точке: функция f непрерывна в точке x0 если limf(x)=f(x0) Формулировка определения предела последовательности такова: «Число А является пределом последовательности если для любого существует номер N, такой, что при всех n>N верно неравенство | ». О. Л. Коши внес также большой вклад в развитие математического анализа. О. Л. Коши хорошо известен каждому человеку, изучавшему математический анализ своими результатами в области математического анализа. Множества в Евклидовом Пространстве Основные метрические понятия п.1 Угол между векторами. Угол между парой векторов x и y мы будем называть тот угол (в пределах от 0 до 1800), косинус которого равен отношению Чтобы это определение можно было применить в общем евклидовом пространстве, необходимо доказать, что указанное отношение по абсолютной величине не превосходит единицы, каковы бы ни были векторы x и y. Для доказательства этого утверждения рассмотрим векторы , где вещественное число. В силу аксиомы о положительно определенной форме скалярного произведения векторов при любом Используя формулу мы можем написать это неравенство в виде В левой части неравенства стоит квадратный трехчлен относительно с постоянными коэффициентами. Трехчлен этот не может иметь различных вещественных корней, так как тогда он не мог бы сохранять знака для всех значений дискриминант этого трехчлена не может быть положительным. Следовательно, откуда ,извлекая квадратный корень, получаем что и требовалось. Неравенство (1) называют неравенством Коши–Буняковского. Примеры. а) В пространстве V3 неравенство Коши–Буняковского, очевидно, вытекает из самого определения скалярного произведения как произведение длин векторов и косинуса угла между ними. б) В пространстве Rn неравенство Коши–Буняковского имеет вид оно справедливо для любой пары векторов и самое, для любых двух систем вещественных чисел и в) В пространстве R2(a,b) неравенство Коши–Буняковского имеет вид Рассмотрим более подробно неравенство Коши в пространстве Rn. Для начала дадим определение n–мерного евклидового пространства Rn .. Def. n–мерное точечное пространство, в котором расстояние между точками определено по данной формуле , называется n–мерным евклидовым пространством и обозначается R n. Ясно, что только тогда, когда x = y, т. е. когда при всех i = 1, 2, .,n. Также ясно, что . Докажем, что для любых трех точек Это неравенство в двумерном или трехмерном пространстве выражает тот элементарный геометрический факт, что сумма двух сторон треугольника не меньше третьей стороны*, и потому называется неравенством треугольника. Также данное неравенство является одним из аксиом метрического пространства и называется аксиомой треугольника Предварительно установим важное неравенство Коши справедливо для любых вещественных чисел ai и bi. Простое доказательство этого неравенства основывается на следующем замечании: если квадратный трехчлен Ax2+2Bx+C с вещественными коэффициентами неотрицателен при всех вещественных x, то его дискриминант Составим вспомогательную функцию от вещественной переменной x, сводящуюся к квадратному трехчлену: где Из определения Тогда, на основании предыдущего замечания, это и есть иначе записанное неравенство Коши. Далее из неравенства (3) выведем еще одно неравенство (ai и bi – любые вещественные числа), которое тоже называют неравенством Коши. Для доказательства неравенства (4) извлечем квадратные корни из обеих частей неравенства (3), затем удвоив обе части полученного нового неравенства и прибавим к ним выражение . В результате получим Это неравенство можно переписать и так: Извлекая, квадратные корни из обеих частей последнего неравенства, получим (4). Теперь уже легко доказать неравенство треугольника (2). Пусть Полагая в неравенстве (4) мы получим неравенство (2). Теперь приведем некоторые примеры метрических пространств. Пусть множество l состоит из всех бесконечных числовых последовательностей удовлетворяющих условию Таким образом, l – метрическое пространство Обозначим через l2 множества всех таких последовательностей вещественных чисел, для которых , и положим Прежде всего нужно проверить, что конечно (т. е. что ря в правой части сходится) для любых x и y из l2. А для этого сначала покажем, что неравенство Коши (4) справедливо и для бесконечных последовательностей чисел ai и b i (i=1, 2, .). Действительно, беря произвольное натуральное n, запишем неравенство (4), а затем перейдем в нем к пределу при . Получим неравенство которое мы будем называть неравенством Коши для бесконечных последовательностей. Аналогичным образом из неравенства (3) выводится и другое неравенство Коши для бесконечных последовательностей: Из неравенства (5), в частности, следует, что если и последовательность , т.е. Теперь проверка выполнения в l2 аксиом метрического пространства может быть произведена совершенно так же, как это сделано для Rn. Пространство l2 иногда называют бесконечномерным евклидовым пространством. п.2 Неравенство треугольника. Если x и y –произвольные векторы, то по аналогии с элементарной геометрии вектор x+y естественно называть третьей стороной треугольника, построенного на векторах x и y. Используя неравенство Коши–Буняковского, мы получаем или Неравенства (7)–(8) называются неравенствами треугольника. Геометрически они означают, что длина любой стороны всякого треугольника не больше, чем сумма длин двух других сторон, и не меньше, чем абсолютная величина разности длин этих сторон. Комплексные пространства со скалярным произведением Скалярное произведение (Основные метрические понятия) п.3 Неравенство Коши–Буняковского. Для любых двух векторов x, y из C имеет место неравенство Доказательство проводится по той же схеме, что и в вещественном случае (п.1), но с некоторой осторожностью обращения с комплексными числами. Если (x, y)=0, неравенство (9) очевидно. При (x, y)¹0 замечаем, что при любом комплексном Будем считать, что изменяется по прямой , симметричной относительно вещественной оси с прямой, определяемой комплексным числом (x, y), так что , где t вещественно, а zo–единичный вектор, определяющий направление прямой , есть вещественное число, так что . Неравенство (10) преобразуется к виду Теперь та же аргументация, что и в (п.1), приводит нас к искомому неравенству (9). Если в неравенстве(9) стоит знак равенства, то трехчлен в левой части (11) имеем один вещественный корень to. Заменяя tzo на что трехчлен в левой части (10) имеет корень , откуда и п.4 Неравенство треугольника. Если x и y – два вектора в унитарном пространстве C, то по неравенству Коши–Буняковского (п.3) откуда Неравенства (12), как и в вещественном случае, называют неравенствами треугольника. Список литературы: 1. Вулих Б. З. Краткий курс теории функций вещественной переменной. М.,1973. – 350 с. 2. Коровкин П. П. Неравенства. М., 1983. – 56 с. 3. Шилов Г.Е. Математический анализ (конечномерные линейные пространства). М.,1969 г., 432 с. 4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, том 2 М., 1966 г., 800с. |
|
© 2010 |
|

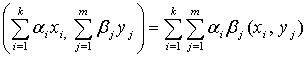 ,
,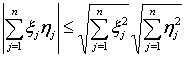 ;
;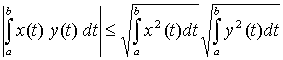 .
.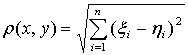
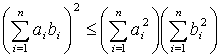 , (3)
, (3)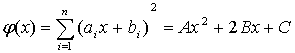 ,
,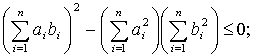
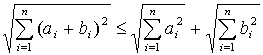 (4)
(4)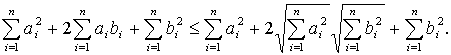
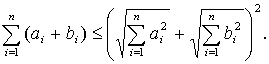
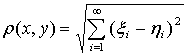 .
.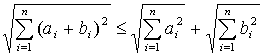 , (5)
, (5)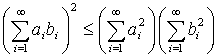 . (6)
. (6)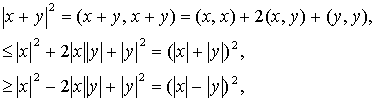
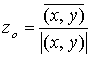 . Тогда
. Тогда 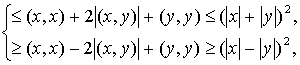
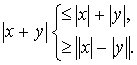 (12)
(12)