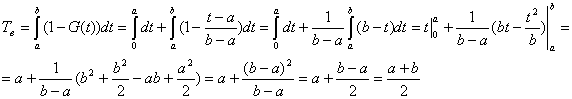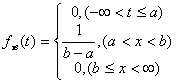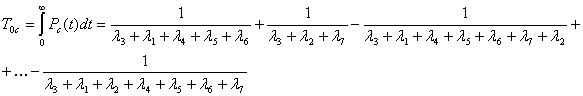|
|
|
|
Курсовая: Обеспечение надежности функционирования КС
Курсовая: Обеспечение надежности функционирования КС
Министерство образования Украины
НТУУ «КПИ»
Кафедра АСОИУ
КУРСОВАЯ РАБОТА
по дисциплине
«ОБЕСПЕЧЕНИЕ НАДЕЖНОСТИ ФУНКЦИОНИРОВАНИЯ КС»
Вариант № 19.
Принял Выполнил
Кузнецов В.Н. студент группы ИС-31
Савчук О.А.
Киев 1998
Задание
Задание 1.
Вычислить восстанавливаемости (ftв (t),V(t), Tв
) системы, если известна функция F(x) распределения времени длительности
восстановления системы. Построить график зависимости плотности ft
в(t) распределения от времени t.
Закон распределения F(x): равномерный.
Определяемый показатель: восстанавливаемость.
Задание 2.
Для одного из видов нагрузки (нагружен, ненагружен) определить показатели λ
c, Pc(t), Qc(t), Toc и Kгс
восстанавливаемой системы, состоящей из 3 типов средств, если известны:
l1= | 10E-4 1/ч | l2= | 10Е-2 1/ч | l3= | 0,1 1/ч | Tв1= | 1 ч | Tв2= | 0,5 ч | Tв3= | 0,25 ч | tp= | 100 ч |
Резерв нагружен.
Схема ССН изображена на рисунке №1.
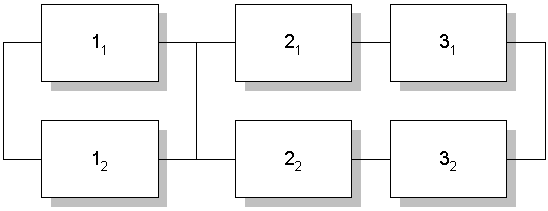 Рис. 1.
Задание 3.
Определить показатели λc и Тос, если известны
вероятности безотказной работы элементов за время t=10 ч, система не
восстанавливаемая:
Рис. 1.
Задание 3.
Определить показатели λc и Тос, если известны
вероятности безотказной работы элементов за время t=10 ч, система не
восстанавливаемая:
P1= | 0,5 | P2= | 0,6 | P3= | 0,7 | P4= | 0,8 | P5= | 0,85 | P6= | 0,9 | P7= | 0,92 |
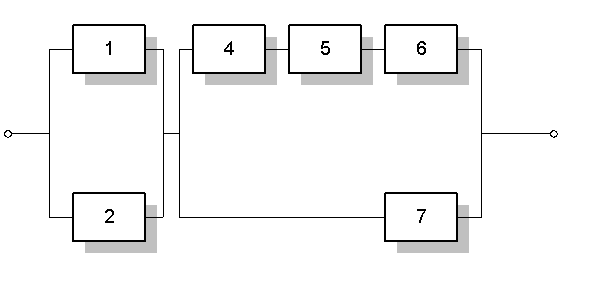
Схема ССН изображена на рисунке №2.
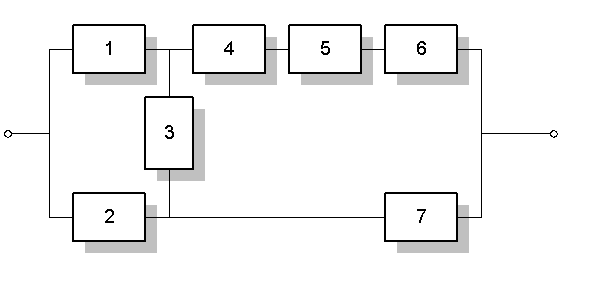 Рис.2.
Задание 4.
Применяя различные виды резервирования (структурное, временное ), для
приведенной в задании 2 структуры обеспечить следующие значения показателей
надежности системы при минимальной ее стоимости:
Т0>=2*103 ч, Кг>=0,99 и P(t)>=0,95 при
t=100 ч, если известны стоимости средств, входящих в систему (в условных
единицах): C1=103; C2=500;C3=100;C
4=50. Стоимость 1 ч резерва времени считать равной 100 у.е.
Рис.2.
Задание 4.
Применяя различные виды резервирования (структурное, временное ), для
приведенной в задании 2 структуры обеспечить следующие значения показателей
надежности системы при минимальной ее стоимости:
Т0>=2*103 ч, Кг>=0,99 и P(t)>=0,95 при
t=100 ч, если известны стоимости средств, входящих в систему (в условных
единицах): C1=103; C2=500;C3=100;C
4=50. Стоимость 1 ч резерва времени считать равной 100 у.е.
Содержание
Задание........................................................................2
Содержание.....................................................................4
Введение.......................................................................5
Расчетная часть................................................................6
Задание 1......................................................................6
Задание 2......................................................................8
Задание 3.....................................................................11
Задание 4.....................................................................14
Выводы........................................................................15
Литература....................................................................16
Введение
В последние годы все больше и больше различная вычислительная техника входит
в нашу жизнь и выполняет все более сложные и ответственные задачи. Сейчас уже
многие опасные и жизненно важные технологические процессы автоматизированы с
использованием вычислительной техники. Это приводит к необходимости
обеспечения высокой надежности и эффективности таких систем.
В данной работе отражаются основные принципы и методы расчета надежности
автоматизированных систем различных структур.
Расчетная часть Задание 1
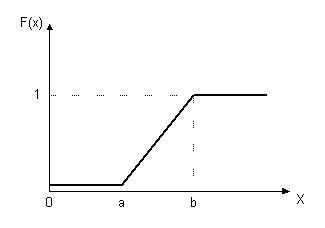
Функция F(x) распределения времени длительности восстановления системы
выглядит следующим образом:
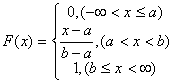 Рис. 3.
Решение.
1. Найдем fτв(t) при различных значениях аргумента.
При -∞ < t £ а fτв(t)=0; при
a £ t < b fτв(t)=F(t)¢
Рис. 3.
Решение.
1. Найдем fτв(t) при различных значениях аргумента.
При -∞ < t £ а fτв(t)=0; при
a £ t < b fτв(t)=F(t)¢
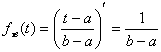 Следовательно
Следовательно
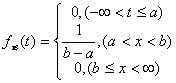 Примем: a=5, b=10
2.
Примем: a=5, b=10
2.
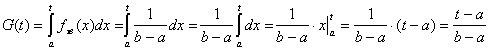 Найдем вероятность восстановления системы за время t - G(t): при -∞
< t £ a G(t)=0; при b £ t £ ∞ G(t)=0; при a
< t < b :
3. Найдем Tв. При -∞ < t £ a Tв=0; при b £ t £ ∞ Tв=1;
при 0 £ t < ∞
Найдем вероятность восстановления системы за время t - G(t): при -∞
< t £ a G(t)=0; при b £ t £ ∞ G(t)=0; при a
< t < b :
3. Найдем Tв. При -∞ < t £ a Tв=0; при b £ t £ ∞ Tв=1;
при 0 £ t < ∞
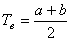 В результате мы получили следующие формулы для вычисления показателей
безотказности системы;
а) плотность распределения длительности восстановления системы fτв(t):
В результате мы получили следующие формулы для вычисления показателей
безотказности системы;
а) плотность распределения длительности восстановления системы fτв(t):
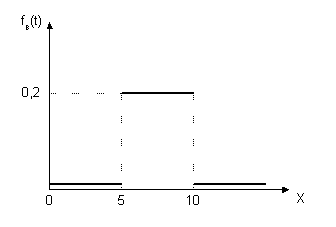 Рис. 4.
на рис. 4 приведен график плотности при a=5, b=10.
б) вероятность восстановления течение времени t
Рис. 4.
на рис. 4 приведен график плотности при a=5, b=10.
б) вероятность восстановления течение времени t
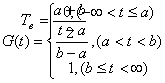 в) среднее время восстановления:
в) среднее время восстановления:
Задание 2
Структура системы приведена на рисунке 1 в задании. А данные следующие:
l1= | 0,0001 1/ч | l2= | 0,01 1/ч | l3= | 0,1 1/ч | Tв1= | 1 ч | Tв2= | 0,5 ч | Tв3= | 0,25 ч | tp= | 100 ч |
Резерв нагружен.
Решение.
Будем использовать алгоритм последовательного структурного укрупнения. Суть
метода состоит в последовательном преобразовании системы. Преобразуем
параллельную часть структуры системы, используя формулы дублирования для
нагруженного резерва:
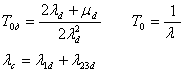 Все преобразования показаны на рисунке 5.
Все преобразования показаны на рисунке 5.
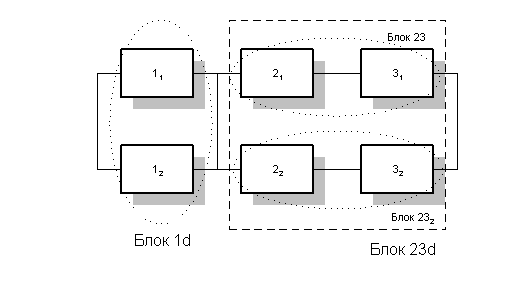 Рис. 5.
Для последовательного включения 2-3 формулы надежности:
Рис. 5.
Для последовательного включения 2-3 формулы надежности:
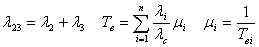 Получаем:
Получаем:
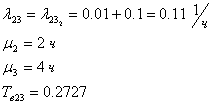 Далее рассчитываем параметры для дублированных элементов 2-3, при
параллельном включении:
Далее рассчитываем параметры для дублированных элементов 2-3, при
параллельном включении:
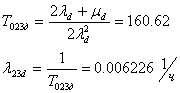
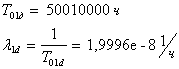 Аналогично для элемента 1:
Предполагаем что время отказа и восстановления системы распределено по
экспоненциальному закону. Используя вышеприведенные формулы, вычислим
интенсивность отказов системы и среднюю наработку на отказ:
λ с= 0,00622589473 1/ч; Toc = 160,619 ч;
Также по формуле для среднего времени восстановления системы при
последовательном соединении 1d и 23d получаем:
Аналогично для элемента 1:
Предполагаем что время отказа и восстановления системы распределено по
экспоненциальному закону. Используя вышеприведенные формулы, вычислим
интенсивность отказов системы и среднюю наработку на отказ:
λ с= 0,00622589473 1/ч; Toc = 160,619 ч;
Также по формуле для среднего времени восстановления системы при
последовательном соединении 1d и 23d получаем:
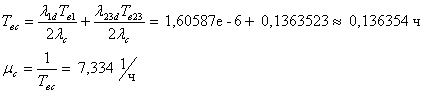 так как интенсивность устранения отказов резервированого узла содержащего k
елементов:
μу = k*μj ;
Вероятность безотказной работы системы:
так как интенсивность устранения отказов резервированого узла содержащего k
елементов:
μу = k*μj ;
Вероятность безотказной работы системы:
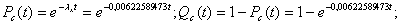 Pc(100)= 0,537; Qc(100)=0,463;
Коэффициент готовности:
Pc(100)= 0,537; Qc(100)=0,463;
Коэффициент готовности:
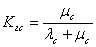 Кгс= 0,999152;
В результате расчетов мы получили следующие показатели надежности:
λ с= 0,00622589473 1/ч;
Toc = 160,619 ч;
Кгс= 0,999152;
Pc(100)= 0,537;
Qc(100)= 0,463;
Кгс= 0,999152;
В результате расчетов мы получили следующие показатели надежности:
λ с= 0,00622589473 1/ч;
Toc = 160,619 ч;
Кгс= 0,999152;
Pc(100)= 0,537;
Qc(100)= 0,463;
Задание 3
Структура системы отображена на рис. 2 в задании.
Решение.
Будем использовать алгоритм последовательного структурного укрупнения. Суть
метода состоит в последовательном преобразовании системы. Преобразуем
заданнную структуру в структуру с последовательным соединением элементов. При
этом будем использовать метод разложения булевой функции относительно
«особого» элемента.
Преобразуем схему в две (рис. 6,7.)
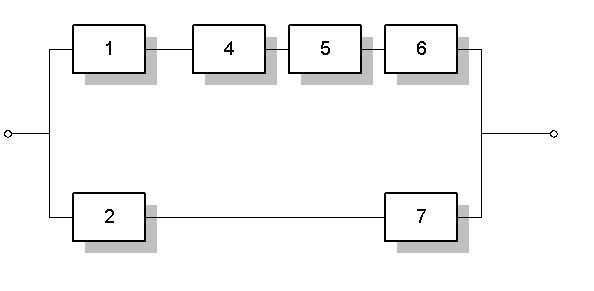 Рис. 6.
Рис. 7.
Таким образом, мы преобразовали функцию B=f(Ai), i=1,7 к следующему виду:
B=A3f(Ai) ÈùA3f(Ai)
Получаем вероятность безотказной работы
P(B)=P(A3f(Ai))+P(ùA3f(Ai))=
P(A3)P(f(Ai/A3))+ P(ùA3
)P(f(Ai/ùA3))= =P3(t) P(f(Ai
), при A3=1)+(1- P3(t)) P(f(Ai), при A3
=0)
Также имеем формулы для последовательного и параллельного соединений:
Рис. 6.
Рис. 7.
Таким образом, мы преобразовали функцию B=f(Ai), i=1,7 к следующему виду:
B=A3f(Ai) ÈùA3f(Ai)
Получаем вероятность безотказной работы
P(B)=P(A3f(Ai))+P(ùA3f(Ai))=
P(A3)P(f(Ai/A3))+ P(ùA3
)P(f(Ai/ùA3))= =P3(t) P(f(Ai
), при A3=1)+(1- P3(t)) P(f(Ai), при A3
=0)
Также имеем формулы для последовательного и параллельного соединений:
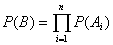 - последовательное - последовательное
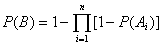 -параллельное
Отсюда получаем, для схемы 1 и 2:
Pcx1= P3(t)* ( 1-(1-P1P4P5P6)(1- P2P7) ).
Pcx2= (1- P3(t))*( (1-(1- P1)(1- P2))*(1-(1-P4P5P6)(1- P7)) ).
И далее , вероятность безотказной работы:
Pc= Pcx1 + Pcx2.
Предполагаем, что время отказа элементов системы распределено по
экспоненциальному закону.
Из соотношения -параллельное
Отсюда получаем, для схемы 1 и 2:
Pcx1= P3(t)* ( 1-(1-P1P4P5P6)(1- P2P7) ).
Pcx2= (1- P3(t))*( (1-(1- P1)(1- P2))*(1-(1-P4P5P6)(1- P7)) ).
И далее , вероятность безотказной работы:
Pc= Pcx1 + Pcx2.
Предполагаем, что время отказа элементов системы распределено по
экспоненциальному закону.
Из соотношения 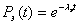 находим находим 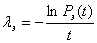 при t=10, получаем:
при t=10, получаем:
P1= | 0,5 | λ1= | 0,0693 | P2= | 0,6 | λ2= | 0,0510 | P3= | 0,7 | λ3= | 0,0356 | P4= | 0,8 | λ4= | 0,0223 | P5= | 0,85 | λ5= | 0,0162 | P6= | 0,9 | λ6= | 0,0105 | P7= | 0,92 | λ7= | 0,0083 |
А время безотказной работы всей системы:
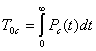
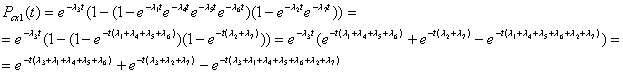 Подставляем полученные фрмулы в интеграл.
В результате расчетов мы получили следующее значение времени безотказной работы:
T0c = 8.4531+10-5.9067+12.8866+16.8634-7.7760-7.8989-
-9.2336+5.6306-7.3746+4.8804-8.8339+6.0901+6.1652+6.9493=
=30,895 ч.
Подставляем полученные фрмулы в интеграл.
В результате расчетов мы получили следующее значение времени безотказной работы:
T0c = 8.4531+10-5.9067+12.8866+16.8634-7.7760-7.8989-
-9.2336+5.6306-7.3746+4.8804-8.8339+6.0901+6.1652+6.9493=
=30,895 ч.
Задание 4
Решение.
Произведем сравнение значений полученных в задании 2 показателей надежности T
oc, Кгс и Pc(t) с приведенными требованиями
Toc = 160,619 ч<2000;
Кгс= 0,999152>0,99;
Pc(100)= 0,537<0.95;
Cравнивая их с требуемыми, видим, что кроме коэффициента готовности,
показатели не обеспечены. Так как стоимость резерва времени меньше стоимости
ненадежного элемента, применим временное резервирование. Для расчета
показателей надежности используются следующие соотношения:
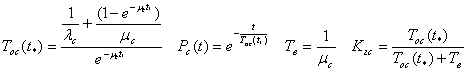 Используя данные соотношения, найдем такое t*,чтобы показатели
надежности соответствовали норме.
Используя данные соотношения, найдем такое t*,чтобы показатели
надежности соответствовали норме.
t* ч | Toc(t*) ч | Pc(100) | Кгс | 1 | 1691,978651 | 0,999409 | 0,999919 | 0,5 | 199,6174595 | 0,997498 | 0,999317 | 0,75 | 405,2974417 | 0,998151 | 0,999664 | 0,625 | 258,3638926 | 0,997584 | 0,999473 | 1,5 | 60094,52894 | 0,999975 | 0,999998 | 1,25 | 9741,126251 | 0,999872 | 0,999986 | 1,1 | 3349,283294 | 0,999672 | 0,999959 | 1,05 | 2370,37751 | 0,999557 | 0,999942 | 1,02 | 1933,929442 | 0,999473 | 0,99993 | 1,03 | 2068,882229 | 0,999502 | 0,999934 | 1,025 | 2000,168795 | 0,999488 | 0,999932 |
Получаем, что при t*=1,025 ч. показатели надежности соответствуют
норме. Продублируем последовательно все элементы цена которых меньше 100у.е.*t
*= 102,5 усл. ед.
Это будет элемент С3 . Дублируем их:
λ4c» 0.0047 1/ч.
Tв» 253.25 ч.
Как видим при дублировании самого дешевого элемента мы не обеспечиваем
требуемые показатели надежности.
Поэтому применим временное резервирование с параметром t*=1,025 ч.
Выводы
В данной работе мы выполнили несколько показательных расчетов, таких как:
· вычисление показателей безотказности/восстанавливаемости системы,
· определение различных параметров восстанавливаемой системы для
нагруженного резерва, состоящей из 3 средств,
· определили параметры надежности системы, содержащей узлы типа
«треугольник»,
· а также применили различные виды резервирования (структурное и
временное) и сравнили их эффективность на примере задачи 2.
В целом данная работа показывает основные принципы анализа надежности
автоматизированных систем.
Литература
1. Методические указания к изучению курса «Прикладная теория
надежности»/Сост.Рожков.- К.:КПИ, 1988.-48с.
2. Надежность АСУ: Учеб.пособие для ВУЗов /Под ред. Я.А.Хотагурова.-М.:
Высш.шк., 1985.-168 с.
3. Конспект лекций по курсу «Теория надежности»
|
|
|
|
|

 Рис. 1.
Задание 3.
Определить показатели λc и Тос, если известны
вероятности безотказной работы элементов за время t=10 ч, система не
восстанавливаемая:
Рис. 1.
Задание 3.
Определить показатели λc и Тос, если известны
вероятности безотказной работы элементов за время t=10 ч, система не
восстанавливаемая:
 Рис.2.
Задание 4.
Применяя различные виды резервирования (структурное, временное ), для
приведенной в задании 2 структуры обеспечить следующие значения показателей
надежности системы при минимальной ее стоимости:
Т0>=2*103 ч, Кг>=0,99 и P(t)>=0,95 при
t=100 ч, если известны стоимости средств, входящих в систему (в условных
единицах): C1=103; C2=500;C3=100;C
4=50. Стоимость 1 ч резерва времени считать равной 100 у.е.
Рис.2.
Задание 4.
Применяя различные виды резервирования (структурное, временное ), для
приведенной в задании 2 структуры обеспечить следующие значения показателей
надежности системы при минимальной ее стоимости:
Т0>=2*103 ч, Кг>=0,99 и P(t)>=0,95 при
t=100 ч, если известны стоимости средств, входящих в систему (в условных
единицах): C1=103; C2=500;C3=100;C
4=50. Стоимость 1 ч резерва времени считать равной 100 у.е.
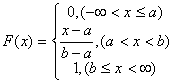 Рис. 3.
Решение.
1. Найдем fτв(t) при различных значениях аргумента.
При -∞ < t £ а fτв(t)=0; при
a £ t < b fτв(t)=F(t)¢
Рис. 3.
Решение.
1. Найдем fτв(t) при различных значениях аргумента.
При -∞ < t £ а fτв(t)=0; при
a £ t < b fτв(t)=F(t)¢
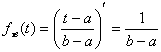 Следовательно
Следовательно
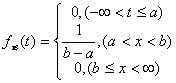 Примем: a=5, b=10
2.
Примем: a=5, b=10
2.
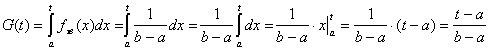 Найдем вероятность восстановления системы за время t - G(t): при -∞
< t £ a G(t)=0; при b £ t £ ∞ G(t)=0; при a
< t < b :
3. Найдем Tв. При -∞ < t £ a Tв=0; при b £ t £ ∞ Tв=1;
Найдем вероятность восстановления системы за время t - G(t): при -∞
< t £ a G(t)=0; при b £ t £ ∞ G(t)=0; при a
< t < b :
3. Найдем Tв. При -∞ < t £ a Tв=0; при b £ t £ ∞ Tв=1;
 Рис. 4.
на рис. 4 приведен график плотности при a=5, b=10.
б) вероятность восстановления течение времени t
Рис. 4.
на рис. 4 приведен график плотности при a=5, b=10.
б) вероятность восстановления течение времени t
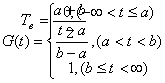 в) среднее время восстановления:
в) среднее время восстановления:
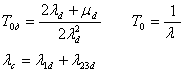 Все преобразования показаны на рисунке 5.
Все преобразования показаны на рисунке 5.
 Рис. 5.
Для последовательного включения 2-3 формулы надежности:
Рис. 5.
Для последовательного включения 2-3 формулы надежности:
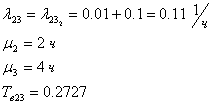 Далее рассчитываем параметры для дублированных элементов 2-3, при
параллельном включении:
Далее рассчитываем параметры для дублированных элементов 2-3, при
параллельном включении:
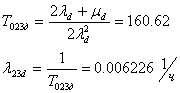
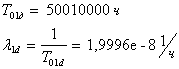 Аналогично для элемента 1:
Предполагаем что время отказа и восстановления системы распределено по
экспоненциальному закону. Используя вышеприведенные формулы, вычислим
интенсивность отказов системы и среднюю наработку на отказ:
λ с= 0,00622589473 1/ч; Toc = 160,619 ч;
Также по формуле для среднего времени восстановления системы при
последовательном соединении 1d и 23d получаем:
Аналогично для элемента 1:
Предполагаем что время отказа и восстановления системы распределено по
экспоненциальному закону. Используя вышеприведенные формулы, вычислим
интенсивность отказов системы и среднюю наработку на отказ:
λ с= 0,00622589473 1/ч; Toc = 160,619 ч;
Также по формуле для среднего времени восстановления системы при
последовательном соединении 1d и 23d получаем:
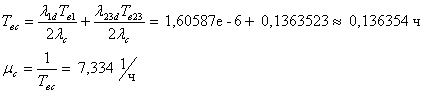 так как интенсивность устранения отказов резервированого узла содержащего k
елементов:
μу = k*μj ;
Вероятность безотказной работы системы:
так как интенсивность устранения отказов резервированого узла содержащего k
елементов:
μу = k*μj ;
Вероятность безотказной работы системы:
 Рис. 6.
Рис. 6.
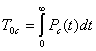
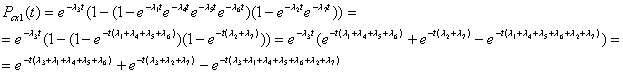 Подставляем полученные фрмулы в интеграл.
Подставляем полученные фрмулы в интеграл.
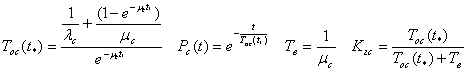 Используя данные соотношения, найдем такое t*,чтобы показатели
надежности соответствовали норме.
Используя данные соотношения, найдем такое t*,чтобы показатели
надежности соответствовали норме.