 |
РУБРИКИ |
Курсовая: Обработка результатов экспериментов и наблюдений |
РЕКОМЕНДУЕМ |
||
|
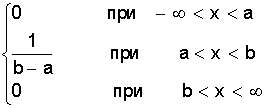
Курсовая: Обработка результатов экспериментов и наблюдений= ( мм2 ); Sa = 7, 35×10-3 мм. При a = 0,95 имеем Dх = ta×Sa = ± 2,26×7,35×10-3 = ± 1,7×10-2 ( мм ); εа = а = 14, 819 ± 0, 017 мм. При a = 0,99 получаем Dх = ta×Sa = ± 3,25×7,35×10-2 = ± 2,4×10-2 ( мм ); εа = а = 14, 819 ± 0, 024 мм. Видно, что абсолютная и относительная погрешность результата десяти измерений стали почти в два раза меньше погрешностей пяти измерений. Применение нормального распределения с s2 = S2n дает в случае a = 0,95 ka = 1,96 и Dх = 1,4 × 10- 2 мм, а величина надежности понижается до 0,91; в случае a = 0,99 получаем ka = 2,58 и Dх = 1,9 × 10-2 мм, а величина надежности понижается до a = 0,97. Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы 1. Цель математической обработки результатов эксперимента; 2. Виды измерений; 3. Типы ошибок измерения; 4. Свойства случайных ошибок; 5. Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является вероятнейшим значением? 6. Что такое истинная абсолютная и вероятнейшая ошибки отдельного измерения? 7. Что такое доверительный интервал случайной величины? 8. Что такое уровень значимости (надежности) серии измерений? 9. Геометрический смысл уровня значимости; 10. Почему при малом числе опытов нельзя погрешность измерений представить в виде Dх = ± Ksа? 11. Что является критерием “случайности” большого отклонения измеряемой величины? 12. Чем определяется величина случайной ошибки косвенных измерений? 13. Чем определяется точность числовой записи случайной величины? 2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН При характеристике случайных величин недостаточно указать их возможные значения. Необходимо еще знать насколько часто возникают различные значения этой величины. Это характеризуется вероятностью p отдельных ее значений. Соотношение, устанавливающее связь между значениями случайной величины и вероятностями этих значений, называют законом распределения случайной величины. Различают интегральный и дифференциальный законы распределения. 2.1. Виды случайных величин и законы их распределения Под случайной величиной понимается величина, принимающая в результате опыта какое либо числовое или качественное значение. Случайная величина, принимающая конечное число или последовательность различных значений, называется дискретной случайной величиной. Случайная величина, принимающая все значения из некоторого интервала, называется непрерывной случайной величиной. Под интегральным законом распределения (или функцией распределения) F (х) случайной величины Х понимают вероятность p того, что случайная величина Х не превысит некоторого ее значения х F (х) = p (Х < х). Основным свойством интегрального распределения является монотонное не убывание в ограниченном диапазоне [ 0; 1 ]. Действительно, если х1 и х2 некоторые значения случайной величины Х. Причем х2 > х1, то очевидно, что событие p (Х < х2) ³ p (Х < х1), т.к. между значениями х 1 и х2 могут быть и промежуточные. Из определения интегрального закона следует, что F (х2) ³ F (х1), что говорит о монотонном не убывании функции. Очевидно также, что F (- ¥) = p (Х < - ¥) = 0; Þ F (¥) - F (- ¥) = 1, F (+ ¥) = p (Х < ¥) = 1; т.е. F (х) изменяется в диапазоне от 0 до 1. Закон распределения дискретной случайной величины может быть задан таблицей или ступенчатой функцией (рис. 4) Рис. 4. Интегральный закон распределения дискретной случайной величины Для дискретной случайной величины F (x) = P (X < x) = P (-¥ < X < x) = распространяется на хi < х. В промежутке между двумя последовательными значениями Х функция F (х) постоянна. При переходе аргумента х через значение хi F (х) скачком возрастает на величину p (Х = х i). Рассмотрим p (х1 £ Х < х2). Если х2 > х1, то очевидно, что p (Х < х2) = p (Х < х1) + p (х1 £ Х < х2). Тогда p (х1 £ Х < х2) = p (Х < х2) - p (Х < х1) = F (х2) - F (х1), т.е. вероятность попадания случайной величины в интервал [х1; х2 ) равен разности значений интегральной функции граничных точек. Последнее условие можно использовать для нахождения вероятности p (Х = х1 ) для непрерывной случайной величины. Для этого рассмотрим предел p (X = x1) = , т.е. если закон распределения случайной величины есть функция непрерывная, то вероятность того, что случайная величина примет заранее заданное значение, равна нулю. Здесь видно различие между дискретными и непрерывными случайными величинами. Для дискретных случайных величин, для каждого значения случайной величины существует своя вероятность. И для него справедливо утверждение: событие, вероятность которого равна нулю, невозможно. Для непрерывной случайной величины это утверждение неверно. Как показано, вероятность того, что Х = х1 ( где х1- заранее выбранное число) равна нулю, это событие не является невозможным. Рассмотрим непрерывную случайную величину Х, интегральный закон которой предполагается непрерывным и дифференцируемым. Функцию ¦ (х) = F¢ (õ) называют дифференциальным законом распределения или плотностью вероятности случайной величины Х. Из определения производной можно записать ¦ (x) = F¢ (x) = , т.е. плотность вероятности случайной величины Х в точке х равна пределу отношения вероятности попадания величины Х в интервал (х; х + Dх) к Dх, когда Dх стремится к нулю. Используя понятия интегральной функции распределения и определенного интеграла можно записать ¦ (x) = F¢ (x) или F (x) = p (x1 < X < x2) = Это соотношение имеет простое геометрическое толкование (рис. 5). Если p (х < Х < х + Dх) » ¦ (х) Dх. Рис. 5. Геометрический смысл дифференциальной функции распределения Из свойств интегрального распределения следует Зная дифференциальный закон распределения можно определить интегральный закон распределения F (x) = 2.2. Числовые характеристики случайных величин, заданных своими распределениями Основными характеристиками случайной величины, заданной своими распределениями, является математическое ожидание ( или среднее значение ) и дисперсия. Математическое ожидание случайной величины является центром ее распределения. Дисперсия характеризует отклонение случайной величины от ее среднего значения. Если Х дискретная случайная величина, значения хi которой принимают с вероятностью pi, так, что , то математическое ожидание М (Х) случайной величины Х определяется равенством M (X) = т.е. суммой произведений всех ее возможных значений на соответствующие вероятности. Математическим ожиданием непрерывной случайной величины является аналог его дискретного выражения M (X) = Действительно, все значения в интервале (х; х + Dх) можно считать примерно равными х, а вероятность таких значений равна ¦ (х) dx (см. ранее). Поэтому значения хi дискретного распределения заменяются х, а вероятности p i - на ¦ (х) dx, а сумма заменяется интегралом. Дисперсией или рассеянием случайной величины Х называется математическое ожидание квадрата разности случайной величины и ее математического ожидания. D (Х) = М [Х - М (Х)]2 = М (Х - х)2 = s2 (х) Если случайная величина Х дискретна и принимает значения хi с вероятностями pi, то случайная величина (Х - х)2 принимает значения (хi - х)2 с вероятностями Рi . Поэтому для дискретной случайной величины имеем D (X) = Аналогично для непрерывной случайной величины получаем D (X) = Чем меньше величина дисперсии, тем лучше значения случайной величины характеризуются ее математическим ожиданием. 2.3. Основные дискретные и непрерывные законы распределения Как отмечалось ранее, очень часто случайная величина распределена по нормальному закону. Но существуют и другие распределения, имеющие практическое значение. Рассмотрим некоторые из них по условиям возникновения и основным параметрам их характеризующим. 1. Равномерное распределение вероятностей. Пусть плотность вероятности А равна нулю всюду, кроме интервала (a; b), на котором она постоянна (рис. 6). Тогда можно записать p (a < X < b) = Рис. 6. Дифференциальный и интегральный законы равномерного распределения Тогда дифференциальный закон равномерного распределения определяется ¦ (x) = Интегральный закон распределения F (x) = . При х ³ b имеем F (x) = Таким образом интегральный закон равномерного распределения задается (рис. 6) F (x) = Основные характеристики распределения М (X) = ; D(X) = = = 2. Биноминальное распределение Пусть при некотором испытании событие А может наступить или не произойти (А). Обозначим вероятность А через р, а А через q = 1 -р ( других итогов испытания нет ). Тогда исходами двух последовательных независимых испытаний и их вероятностью будут: АА - р2; АА - рq; АА - qр; АА - q2. Отсюда видно, что двукратное появление события А равно р2, вероятность однократного появления - 2 рq, а вероятность того, что А не наступит ни разу - q2. Эти результаты единственно возможные и поэтому Это рассуждение можно перенести на любое число испытаний. Например, при трех испытаниях получим . Подсчитаем вероятность того, что при n испытаниях событие А появится m раз. Это может произойти, например, в последовательности Ясно, что вероятность равна рmqn-m. Но m событий А может быть и в другом сочетании. Число всех возможных сочетаний из n элементов по m (количество событий А) равно числу сочетаний . Используя теорему сложения вероятностей получаем общую вероятность Рm ,n наступления m событий А из n испытаний Pm,n = = Из этой формулы видно, что вероятности Рm,n для различного исхода испытаний (появление или не появление определенного результата А) определяется pn + npn-1q + . Коэффициенты перед вероятностями р, q являются биноминальными коэффициентами, а общая вероятность представляет слагаемые в разложении бинома ( р + q )n . Поэтому закон распределения случайной величины Х, в котором вероятность наступления событий А определяется коэффициентами бинома, называется биноминальным распределением дискретной случайной величины. Этот закон может быть задан в виде таблицы 1. Таблица 1 Биноминальный закон распределения
Биномиальные коэффициенты удобно получать с помощью треугольника Паскаля. 1 n = 0 1 1 n = 1 1 2 1 n = 2 1 3 3 1 n = 3 1 4 6 4 1 n = 4 1 5 10 10 5 1 n = 5 Все строки треугольника ( начинающегося с единицы ) начинаются и заканчиваются единицей. Промежуточные числа получаются сложением соседних чисел вышестоящей строки. Числа, стоящие в одной строке, являются биноминальными коэффициентами соответствующей степени. Из описания биномиального распределения становится ясно, что область его действия там, где возможно многократное проведение испытаний с известной вероятностью. На рис. 7 представлен биномиальный закон распределения. Рис. 7. Биномиальный закон распределения Определим основные характеристики этого распределения. Математическое ожидание М (Х) = + + = np (q + p)n-1 = np. Дисперсия распределения может быть определена из общего выражения но это приводит к громоздким вычислениям. В то же время случайная величина Х принимает в каждом опыте только два значения: 1, если событие А произошло и 0, если оно не произошло с вероятностями, соответственно, р или q. Тогда математическое ожидание одного опыта определится М (Х1) = 0×q + 1×р = р = х и соответственно дисперсия одного опыта D (Х1) = (0 - р)2×q + (1 - р)2×р = р2q + q2р = рq (р + q) = рq. Тогда дисперсия всех n опытов составит D (X) = n×p×q. 3. Закон Пуассона В случае малых р ( или, наоборот, близких к 1 ) биноминальный закон распределения можно преобразовать следующим образом где . Определим предел Рm,n при n ® ¥ и постоянном m. Тогда пределы Окончательно имеем Это распределение называется законом Пуассона, где l - интенсивность распределения. Используется в задачах с редкими событиями. На рис. 8 представлена схема вероятностей, распределенных по закону Пуассона. Рис. 8. Закон распределения Пуассона Определим его основные характеристики и смысл величины l. Запишем закон распределения в виде таблицы.
M (X) = + . Выражение в скобках есть разложение функции еl в ряд Маклорена. Поэтому М (Х) = lе-lеl = l. Не рассматривая вывод отметим, что D (Х) = l, т.е. дисперсия равна математическому ожиданию. Рассмотренные виды распределений случайной величины, конечно, не исчерпывают всех существующих распределений. Можно назвать еще несколько: распределение Бернулли, экспоненциальное распределение, гамма - распределение, распределение Вейбула, гипергеометрические распределения и др. При определенных условиях и параметрах один вид распределения может переходить в другой. Поэтому при решении практических задач по законам распределения случайных величин следует обращаться к специальной литературе. 2.4. Понятие статистической гипотезы и статистического критерия Статистической гипотезой называют любое утверждение о виде или свойствах распределения наблюдаемых в эксперименте случайных величин. Такие утверждения можно делать на основе теоретических соображений или статистических исследований других наблюдений. Например, при многократном измерении некоторой физической величины, точное значение Х которой не известно, но в процессе измерений оно меняется. На результат измерений влияют многие случайные факторы, поэтому результат i - го измерения можно записать в виде аi = Х + εi, где εi - случайная погрешность измерения. Если εi складывается из большого числа ошибок, каждая из которых не велика, то на основании центральной предельной теоремы можно предположить, что случайные величины аi имеют нормальное распределение. Такое предположение является статистической гипотезой о виде распределения наблюдаемой случайной величины. Если для исследуемого явления сформулирована та или иная гипотеза ( обычно ее называют основной или нулевой гипотезой и обозначают символом Но ), то задача состоит в том, чтобы сформулировать правило, которое позволяло бы по результатам наблюдений принять или отклонить эту гипотезу. Правило, согласно которому проверяемая гипотеза Но принимается или отвергается, называется статистическим критерием проверки гипотезы Но . Наиболее распространены такие статистические гипотезы, как: а) вида распределения; б) однородности нескольких серий независимых результатов; в) случайности результатов эксперимента и т.п. Статистический критерий проверки гипотезы Но служит для определения возможного отклонения от основной гипотезы. Характер отклонений может быть различным. Если критерий ²улавливает² любые отклонения от Но , то такой критерий называют универсальным или критерием согласия. Существуют критерии, которые выявляют отклонения от заданного вида, это узко направленные критерии. Выбор правила проверки гипотезы Но эквивалентен заданию критической области х1, при попадании в которую переменной х гипотеза Но отвергается. Критерий, определяемый критической областью х1 называют критерием х1. В процессе проверки гипотезы Но можно прийти к правильному решению или совершить ошибку первого рода - отклонить Но когда она верна, или ошибку второго рода - принять Но, когда она ложна. Иными словами, ошибка первого рода имеет место, если точка х попадает в критическую область х1, в то время как верна нулевая гипотеза Но, а ошибка второго рода - когда х Î хо, но гипотеза Но ложна. Желательно провести проверку гипотезы так, чтобы свести к минимуму вероятности обоих ошибок. Однако при данном числе испытаний n в общем случае невозможно одновременно обе эти вероятности сделать как угодно малыми. Поэтому наиболее рационально выбирать критическую область следующим образом: при заданном числе испытаний n устанавливается граница для вероятности ошибки первого рода и при этом выбирается та критическая область х1, для которой вероятность ошибки второго рода минимальна. 2.5. Вероятности ошибок первого и второго рода Рассмотрим станок, который может работать только в одном из двух состояний. Если он работает в налаженном режиме, то для интересующего нас признака качества, например, длины или диаметра заготовки, имеет место нормальное распределение при работе как в налаженном так и в разлаженном режиме. Оба режима отличаются только уровнем настройки процесса по математическому ожиданию ( М(х) = 10 и 11, соответственно в налаженном и разлаженном режиме ), в то время как дисперсии в обоих случаях составляют s2 = 4. Проверить нужно нулевую гипотезу, в соответствии с которой М(х) = 10, против альтернативы ( в данном случае единственной ) М(х) = 11. Конкурирующую гипотезу обозначим Н1. Тогда Но: М(х) = 10; Н1: М(х) = 11. Необходимо по результатам выборки определить в каком из состояний работает станок. Примем объем выборки n из потенциально бесконечной генеральной совокупности. В качестве контрольной величины возьмем выборочное среднее Х n. На рис. 9 изображены плотности распределения Хn для n = 25 и n = 4. Для формулировки критерия необходимо разделить область изменения контрольной величины (х) на критическую область отклонения гипотезы Но ( принятия Н1 ) и область принятия гипотезы Но. Для этого необходимо выбрать число К, такое, что 10 < К < 11, и интервал ( -¥; К ] рассматривать как область принятия гипотезы Но, а интервал [ К; ¥ ) - как область отклонения гипотезы Но. По рис. 9 видно, что каждая реализация Х25 или Х4 возможна при верности любой из двух гипотез, но с различной вероятностью. На рис. 9 указаны вероятности совершения ошибки первого Рис. 9. Плотности распределения двух гипотез при различном объеме выборки и одинаковой дисперсии рода a ( отклонения верной гипотезы Но ) и второго рода b ( принятие гипотезы Но, когда она не верна ). По рис. 9 также видно, что увеличение n ведет к уменьшению дисперсии распределения х и тем самым - к одновременному уменьшению вероятностей a и b. В соответствии с рис. 9 можно записать: ; Эти два уравнения содержат четыре величины a, b, К, n. Задав две из четырех величин, можно определить две другие. Например, при n = 25 и К = 10,4 определим: . Если задаться величинами a и b, то можно определить величины К, n. 2.6. Проверка гипотезы вида закона распределения вероятностей При проверке эксперимента закон распределения вероятностей случайных величин неизвестен и можно лишь предположительно судить о его виде . Выборочные оценки параметров распределения несут в себе случайные ошибки, искажающие истинный характер распределения. Поэтому после получения эмпирического распределения производится подбор теоретического закона распределения, пригодного для описания вероятностных свойств изучаемой случайной величины. Критерии подбора ( проверки гипотезы соответствия ) называют в статистике критериями согласия. Все они основаны на выборе допустимой меры расхождения между теоретическим распределением и выборочными данными. Общую процедуру проверки гипотезы закона распределения можно представить в следующей последовательности: 1. По опытным данным строится эмпирическая кривая распределения вероятностей; 2. Определяются параметры эмпирического распределения ( в соответствии с его видом ); 3. Выдвигается одна или несколько гипотез о функции плотности исследуемой случайной величины, исходя из внешнего вида эмпирической кривой, значений ее параметров, технических факторов, влияющих на ее вид; 4. Эмпирическая кривая выравнивается по одной или нескольким теоретическим кривым; 5. Проводится сравнение по одному или нескольким критериям согласия; 6. Выбирается теоретическая функция, дающая наилучшее согласование. Поясним п. 4; 5. Определив по эмпирическим данным параметры распределения, подставляют их в теоретическую кривую закона распределения и рассчитывают вероятность середин интервалов эмпирического распределения. Умножив значение полученной вероятности на общее число опытов, получают теоретическое значение частот случайной величины, которые и определяют ²выровненную² кривую. Теперь можно найти вероятность того, что эмпирическая кривая соответствует выбранной теоретической, выбрав вероятность согласия ( уровень значимости ). Если результат расхождения не выйдет за принятый уровень значимости, то считают, что эмпирическое распределение согласуется с теоретическим. Если сравнение осуществляется с несколькими теоретическими законами, то окончательно принимать тот, который дает лучшее соответствие. Чаще всего в качестве критериев согласия принимают критерий Пирсона ( c2 ) и критерий Колмогорова - Смирнова ( К - С - критерий ). Критерий c2 является наиболее состоятельным при большом числе наблюдений. Он почти всегда опровергает неверную гипотезу, обеспечивает минимальную ошибку в принятии неверной гипотезы по сравнению с другими критериями. c2 = где mj - наблюдаемая частота случайного события; m*j - ожидаемая по принятому теоретическому закону распределения; К - число интервалов случайной величины. Затем определяется число степеней свободы l: l = К - r - 1; где К - число интервалов случайной величины; r - число параметров теоретической функции распределения. К - С - критерий лучше всего использовать в случае, если теоретические значения параметров распределения известны. При неизвестных параметрах его можно использовать, но он дает несколько завышенные результаты. При использовании этого критерия определяется величина где mнj, m*нj - соответственно, накопленные наблюдаемые и ожидаемые (теоретические) частоты; n - число проведенных опытов. То есть, в данном случае оценивается только максимальное отклонение накопленной частоты случайного события, возникающее в одном из диапазонов изменения случайной величины. Полученное значение коэффициента сравнивается с табличным для числа степеней свободы опыта и принятого уровня значимости результата. Если табличное значение коэффициента больше, то гипотеза о принятом законе распределения не отвергается. Контрольные вопросы 1. Сущность непрерывной и дискретной случайной величины; 2. Сущность интегрального закона распределения случайной величины; 3. Сущность дифференциального закона распределения случайной величины; 4. Связь интегрального и дифференциального законов распределения; 5. Основные характеристики случайной величины, заданной своим распределением; 6. Назовите примеры законов распределения непрерывной и дискретной случайной величины; 7. Понятие статистической гипотезы и статистического критерия; 8. Назовите примеры статистических гипотез; 9. Сущность ошибок первого и второго рода; 10. Сущность проверки гипотезы вида закона распределения; 11. Принципиальное различие в критериях Пирсона и Колмогорова - Смирнова. 3. НАХОЖДЕНИЕ ИНТЕРПОЛИРУЮЩИХ КРИВЫХ В первой части пособия рассматривались измерения той или иной физической величины, находящейся при проведении серии измерений в неизменном состоянии. Очень часто исследуемая величина меняется в соответствии с изменением условий опыта или времени. Цель эксперимента в этом случае состоит в нахождении функциональной зависимости, которая наилучшим образом описывает изменение интересующего нас параметра. Следует понимать, что однозначно восстановить ( большей частью неизвестную ) функциональную зависимость между переменными невозможно даже в том случае, если бы переменные величины, полученные из опыта, не имели бы ошибки измерения. Тем более не следует ожидать, что это удастся сделать, имея экспериментальные данные, содержащие, по крайней мере, случайные ошибки измерений. Поэтому математическая обработка результатов наблюдений не может ставить перед собой задачу разгадать истинный характер зависимости между переменными. Она позволяет лишь представить результаты опыта в виде наиболее простой формулы. В зависимости от назначения этих формул существуют различные методы их получения, отличающиеся сложностью расчетных процедур и точностью получаемых решений. 3.1. Графический метод обработки результатов Графический метод заключается в построении графика зависимости между исследуемыми величинами с последующим определением уравнения зависимости между ними. Графики строят прежде всего в равномерных шкалах. Если характер связи между исследуемыми величинами неизвестен, то сначала проверяют совпадение экспериментальных точек с заданной кривой. Если предварительные сведения о характере уравнения отсутствуют, то первым этапом обработки данных является нахождение кривой, совпадающей с опытными точками. Эта задача решается методом подбора. Можно использовать эталон - кальку с предварительно вычерченным на ней семейством кривых с различными параметрами. Естественно, что масштаб кальки и эмпирической кривой должен быть одинаков. Построенный по опытным данным отрезок кривой может совпадать с большим количеством различных кривых, проходящих достаточно близко к опытным точкам. В этом случае выбирают кривую с наиболее простым и удобным в использовании уравнением. Иногда эмпирическая кривая может иметь перегибы или состоять из отдельных ярко выраженных участков. Однако при этом необходимо определить координаты точек перехода от одной кривой к другой. Уравнение зависимости между исследуемыми величинами при графическом методе просто определяется тогда, когда эмпирические точки достаточно хорошо совпадают с прямой линией, т.е. описываются уравнением y = ax + b, где a, b - коэффициенты, подлежащие определению. Определение коэффициентов при графическом методе основано на ²способе натянутой нити². Нанеся результаты эксперимента на график (лучше, если он выполнен на миллиметровке), подбираем графическую прямую, ближе всего подходящую к нанесенным точкам. Выбрав положение прямой, определяем две произвольные точки на этой прямой (не обязательно являющиеся точками эксперимента), определяем их координаты (x1; y1), (х 2; y2). И для определения коэффициентов а и b получаем два простых уравнения ах1 + b = y1; ах2 + b = y2. На рис. 10 приведена иллюстрация этого метода. Точки - результаты, полученные в эксперименте. Прямая проведена на глаз как можно ближе к экспериментальным точкам. На прямой выбраны точки М (2; 4) и N (13; 10). Коэффициент а характеризует угол наклона прямой. Поэтому . Таким образом y = 0,55х + 2,9. Рис. 10. Графический метод интерполяции В случае, если экспериментальная зависимость имеет нелинейный характер, то графическим способом в системе координат с равномерными шкалами определить коэффициенты кривой затруднительно. Но достаточно большой класс нелинейных зависимостей путем замены переменных и графического изображения в функциональных шкалах можно привести к линейным и далее использовать способ натянутой нити. 3.2. Функциональные шкалы и их применение Пусть функция y = ¦(х) непрерывна и монотонна на некотором промежутке [ a; b ]. Возьмем ось ОМ, на которой будет строиться шкала, выберем на ней точку начала отсчета О и установим масштаб m. Функциональная шкала строится следующим образом. Разбив интервал [ а; b ] на равные части, вычисляем значение функции ¦(х) в каждой из точек деления и отложим на оси ОМ для каждой точки отрезок m¦(х). Получающаяся при этом точка снабжается отметкой х, т.е. откладывается в выбранном масштабе значение функции, а надписывается значение аргумента. Иногда начало шкалы помещают в первую точку отсчета, т.е. точку с надписью а совмещают с 0. Тогда точка х будет находиться в конце отрезка m [ ¦(х) - ¦(а) ]. Полученная шкала позволяет судить о поведении функции на рассматриваемом участке: большие промежутки между отметками укажут, что функция изменяется быстрее, чем там, где эти промежутки малы. Выбор масштаба m определяет длину шкалы. Чаще поступают наоборот: задаются длиной шкалы l и определяют масштаб. Пример. Построим функциональную шкалу для функции y = x2 на участке [ 1; 2 ]. Зададимся длиной шкалы l = 12 см. Тогда m = см. Разобьем отрезок [ 1; 2 ] на десять равных частей и вычислим значения функции во всех точках деления. Совместим начало шкалы с точкой отсчета х = 1. Результаты расчета сведены в табл. 2, а функциональная шкала приведена на рис. 11. Таблица 2 Расчет функциональной шкалы y = x2
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
;
;
,
где суммирование
.
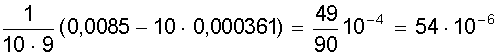
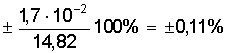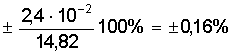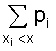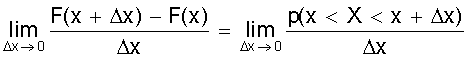
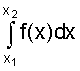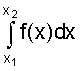определяет заштрихованную область в соответствующих пределах, то
.
.
,
.
.
.
A = 
.
.
.
.
,
,
.
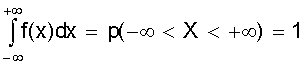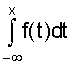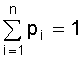
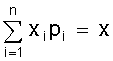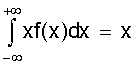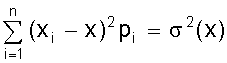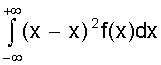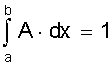
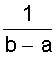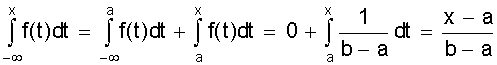
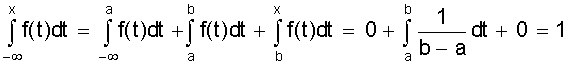
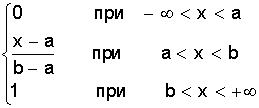
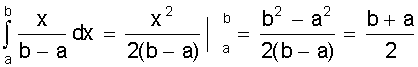
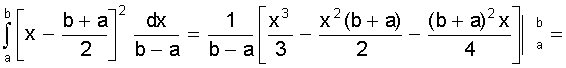
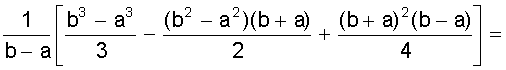
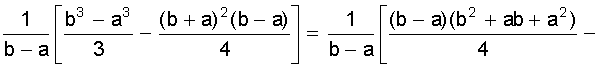
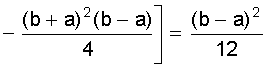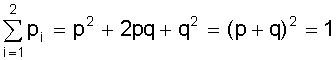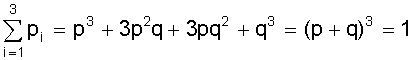
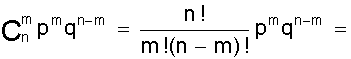
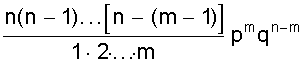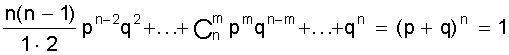
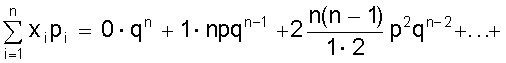
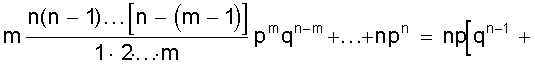
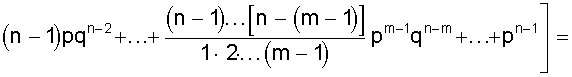
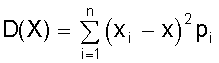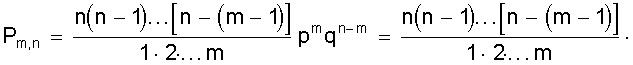
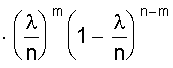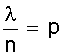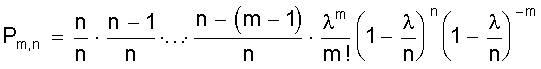
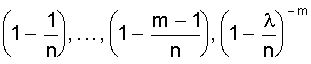равны единице, а 
.
.
.
;
,
,
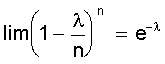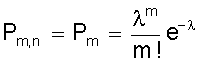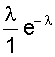
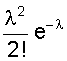
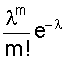
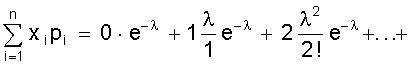
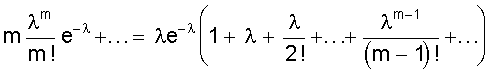
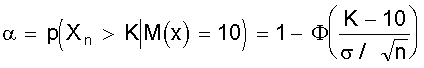
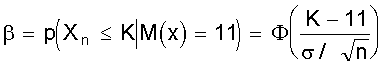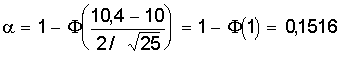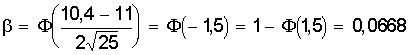
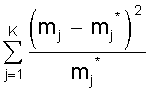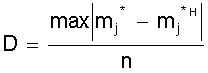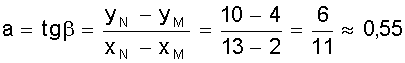
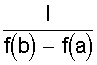Þ m = 
.
© 2010 |
|