|
|
|
|
Лекция: Конспект лекций по дискретной математике
Лекция: Конспект лекций по дискретной математике
Приложение Булевой алгебры к синтезу комбинационных схем
Двоичная система логики:
1. Элементы Булевой алгебры:
а) числа
b) переменные
с) операции
d) выражения
e) функции
f) законы
А) Числа:
Два числа: логический ноль и логическая единица в Булевой алгебре
отождествляются с понятиями “истина” и ”ложь”.
В) Переменные:
Булевы (логические, двоичные) переменные называются переменными, принимающими
значение из множества - ноль и единица.
С) Операции:
1. Отрицание (инверсия).
2. Конъюнкция (логическое умножение).
3. Дизъюнкция (логическое сложение).
Унарной является операция отрицания.
Обозначения:
1. Отрицание 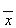 , ù x
2. Конъюнкция a&b, a·b, ab, aÙb
3. Дизъюнкция aÚb
D) Выражения:
Переменные, знакооперации, соединенные вместе при возможном наличии скобок
для задания порядка выполнения операций.
Приоритет задается порядком операции.
Е) Функции:
Булевой (логической) функцией называется такая функция, аргументами которой
являются булевы переменные, и сама функция принимает значение из множества
ноль и единица.
Областью определения Булевой функции является совокупность 2n
двоичных наборов ее аргументов. Набор аргументов можно рассматривать как
n-компонентный двоичный вектор.
Формы задания Булевой функции:
1. Аналитическая (в виде логического выражения)
2. Табличная (в виде таблицы истинности)
3. Графическая
4. Таблично-графическая (в виде карты Карно)
5. Числовая
6. Символическая форма
1) Аналитическая:
_ _
y=(x1 Ú x2) x3
_ _ _ _ _ _
y=x1 x2 x3 Ú x1 x2 x3 Ú x1 x2 x3
2) Табличная: , ù x
2. Конъюнкция a&b, a·b, ab, aÙb
3. Дизъюнкция aÚb
D) Выражения:
Переменные, знакооперации, соединенные вместе при возможном наличии скобок
для задания порядка выполнения операций.
Приоритет задается порядком операции.
Е) Функции:
Булевой (логической) функцией называется такая функция, аргументами которой
являются булевы переменные, и сама функция принимает значение из множества
ноль и единица.
Областью определения Булевой функции является совокупность 2n
двоичных наборов ее аргументов. Набор аргументов можно рассматривать как
n-компонентный двоичный вектор.
Формы задания Булевой функции:
1. Аналитическая (в виде логического выражения)
2. Табличная (в виде таблицы истинности)
3. Графическая
4. Таблично-графическая (в виде карты Карно)
5. Числовая
6. Символическая форма
1) Аналитическая:
_ _
y=(x1 Ú x2) x3
_ _ _ _ _ _
y=x1 x2 x3 Ú x1 x2 x3 Ú x1 x2 x3
2) Табличная:
x1 | x2 | x3 | _ x1 Ú x2 | y | | 0 | 0 | 0 | 1 | 1 | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 1 | | 0 | 1 | 1 | 1 | 0 | | 1 | 0 | 0 | 0 | 0 | | 1 | 0 | 1 | 0 | 0 | | 1 | 1 | 0 | 1 | 1 | | 1 | 1 | 1 | 1 | 0 |
Переход от аналитической к табличной однозначен! Обратный переход не является
однозначным.
Основные законы (тождества)
1) ab=ba
aÚb=bÚa
2) Ассоциативный:
a(bc)=(ab)c
aÚ(bÚc)= (aÚb) Úc
3) Дистрибутивный:
a(bÚc)=abÚac
aÚ(bc)=(aÚb)(aÚc)
4) Закон двойного отрицания:
=
a=a
5) Тавтологии:
aa=a
aÚa=a
6) Законы нулевого элемента:
a0=0
aÚ0=a
7) Законы единичного элемента:
а1=а
аÚ1=1
8) Законы дополнительного элемента:
_
В Булевой алгебре дополнительным элементом к а является а.
_ _
аÚа=1; аа=0
9) Двойственности (деМоргана):
__ _ _
ab=aÚb
___ _ _
aÚb=a b
Cледствия: ab=aÚb; aÚb=a b
10) Поглощения:
aÚab=a
a(aÚb)=a
11) Сокращения:
_
аÚаb=aÚb
_
a(aÚb)=ab _ _ _ _
Cледствия: aÚab=aÚb; a(aÚb)=ab
12) Склеивания:
_ _
abÚab=a; (aÚb)(aÚb)=a
Комментарии:
1) Для доказательства законов можно использовать:
а) Метод совершенной индукции.
б) Использование одних законов для доказательства других законов.
Метод совершенной индукции состоит в доказательстве эквивалентности левой и
правой части на всем множестве наборов аргументов. Для этого составляется
таблица истинности.
2) Большинство законов задается парой соотношений, при этом одно соотношение
можно получить из другого заменив операции конъюнкции на дизъюнкцию или
дизъюнкцию на конъюнкцию (метод не применим в законах, в которых участвуют
константы). С константами же константы заменяются на противоположные
значения. (Дуальность законов Булевой алгебры)
3) Некоторые законы можно распространять на произвольное число элементов.
4) В любом законе можно заменить любую букву на произвольное логическое
выражение.
5) Законы применяются для упрощения Булевых функций.
Разнообразие Булевых функций.
1. Булева функция от одной переменной.
| Обозначение аргумента и функции | Значения аргумента и функции | Наименование функции | | x | 0 | 1 | | 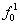
| 0 | 0 | Логический ноль | 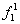
| 0 | 1 | Повторение x | 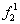
| 1 | 0 | Инверсия x | 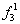
| 1 | 1 | Логическая единица |
2. Возможные функции от двух переменных.
| Обозначение аргументов и функций | Значение аргументов и функций | Обозначение функций | Наименование | Вырожденность | Представление функции в булевом базисе | 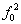
| 0 | 0 | 0 | 0 | “0” | Логический ноль | + | - | 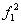
| 0 | 0 | 0 | 1 | x1&x2 | Конъюнкция | - | x1 x2 | 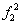
| 0 | 0 | 1 | 0 | x1Dx2 | Запрет x1 по x2 | - | x1 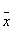 2 2 | 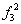
| 0 | 0 | 1 | 1 | x1 | Повторение x1 | + | - | 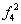
| 0 | 1 | 0 | 0 | x2Dx1 | Запрет x2 по x1 | - | x2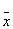 1 1 | 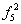
| 0 | 1 | 0 | 1 | x2 | Повторение x2 | + | - | 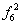
| 0 | 1 | 1 | 0 | x1Åx2 | Сумма по модулю 2 неравнозначная (исключительное или) XOR | - | 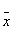 1 x2 Ú x1 1 x2 Ú x1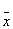 2 2
| 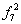
| 0 | 1 | 1 | 1 | x1Úx2 | Дизъюнкция | - | x1 Ú x2 | 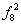
| 1 | 0 | 0 | 0 | x1¯x2 | Функция Вебба | - | x1Úx2 | 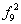
| 1 | 0 | 0 | 1 | x1ºx2 | Равнозначность | - | 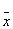 1 1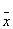 2 Ú x1 x2 2 Ú x1 x2
| 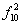
| 1 | 0 | 1 | 0 | 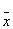 2 2
| Отрицание x2 | + | - | 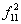
| 1 | 0 | 1 | 1 | x2®x1 | Импликация от x2 к x1 | - | 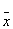 2 Ú x1 2 Ú x1
| 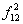
| 1 | 1 | 0 | 0 | 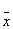 1 1
| Отрицание x1 | + | - | 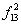
| 1 | 1 | 0 | 1 | x1®x2 | Импликация x1 к x2 | - | 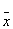 1 Ú x2 1 Ú x2
| 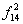
| 1 | 1 | 1 | 0 | x1 | x2 | Штрих Шеффера | - | 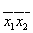
| 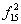
| 1 | 1 | 1 | 1 | “1” | Логическая единица | + | - |
Определение: Булева функция от n аргументов fn(x) называется
вырожденной по аргументу xi, если ее значение не зависит от этого
аргумента, то есть для всех наборов аргументов имеет место равенство:
f(x1, x2, ... , xi-1, 0, xi+1, ... , xn) = f(x1, x2, xi-1, 1, xi+1, ... , xn).
Функция запрета x1Dx2 принимает значение, равное нулю при
равенстве запрещающей переменной (x2) единице и повторяет значение
аргумента x1 при равенстве запрещающей переменной нулю.
Понятие импликации в Булевой алгебре отождествляется с выражением следования
(если ... то ... ).
Пример: Имеют место два простых высказывания.
А. На небе тучи.
В. Идет дождь. В®А
Из истины не может следовать ложь!
Некоторые функции от трех переменных.
| Значение аргументов | Значение функций | | Сумма по модулю 2 | Исключающее ИЛИ | Функция мажоритарности | x1 | x2 | x3 | x1Åx2Åx3 | XOR (x1,x2,x3) | x1#x2#x3 | | 0 | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 1 | 0 | | 0 | 1 | 1 | 0 | 0 | 1 | | 1 | 0 | 0 | 1 | 1 | 0 | | 1 | 0 | 1 | 0 | 0 | 1 | | 1 | 1 | 0 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 0 | 1 |
Функция - сумма по модулю 2 и исключающее ИЛИ являются эквивалентными только
для двух аргументов.
n
Общее разнообразие функций от n аргументов равно 22
В самом компактном виде любую Булеву функцию можно представить символически: 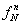 , где n-количество аргументов, а N-десятичный эквивалент двоичного набора
значений функции на упорядоченном множестве аргументов.
Пример:
f3(x)=x1Åx2Åx3=
, где n-количество аргументов, а N-десятичный эквивалент двоичного набора
значений функции на упорядоченном множестве аргументов.
Пример:
f3(x)=x1Åx2Åx3=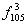 Невырожденные функции от двух переменных с добавлением функции отрицания
принято называть функциями Булевой алгебры. С учетом обращаемости некоторых
базовых функций к некоторым аргументам, их общее количество равно девяти.
Нормальные формы Булевых функций
Нормальные формы - это особый класс аналитических выражений, используемых при
решении задачи минимизации Булевых функций и для перехода от табличной формы
задания к аналитической. Нормальные формы строятся на основании операций
конъюнкции, дизъюнкции и отрицания, причем отрицание только единственной
переменной.
Определение: Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция
(дизъюнкция) конечного числа попарно различимых переменных или их отрицаний.
Элементарную конъюнкцию (дизъюнкцию) принято называть конъюнктивным
(дизъюнктивным) термом.
В частном случае терм, как конъюнктивный так и дизъюнктивный может состоять
из единственной буквы (литерала). Под буквой будем понимать аргумент Булевой
функции и его отрицания.
Примеры конъюнктивных термов:
_ _
x1, x2, x1x3, x2x4x5 (терм)
___ _
x1x2, x1x2x3 (не терм)
Рангом терма называется количество букв входящих в него.
Дизъюнктивной (конъюнктивной) нормальной формой Булевой функции называется
дизъюнкция (конъюнкция) конечного числа попарно различимых конъюнктивных
(дизъюнктивных) термов.
Каноническая нормальная форма.
Конституентой единицы (нуля) называется конъюнктивный (дизъюнктивный) терм
максимального ранга. Т.е. для Булевой функции от n переменных конституента
включает в себя n букв.
Свойство конституенты: Конституента единицы (нуля) принимает значение единицы
(нуля) на одном и только одном наборе аргументов.
Пример: _ _
n=4 x1x2x3x4 (1010)=1
_ _ _
x1Úx2Úx3Úx4=0
Определение: Дизъюнктивная (конъюнктивная) нормальная форма называется
канонической, если все ее дизъюнктивные (конъюнктивные) термы представляют
собой конституенты единицы (нуля). Иногда канонические формы называют
совершенными.
Пример получения канонических форм:
y=x1Åx2
Невырожденные функции от двух переменных с добавлением функции отрицания
принято называть функциями Булевой алгебры. С учетом обращаемости некоторых
базовых функций к некоторым аргументам, их общее количество равно девяти.
Нормальные формы Булевых функций
Нормальные формы - это особый класс аналитических выражений, используемых при
решении задачи минимизации Булевых функций и для перехода от табличной формы
задания к аналитической. Нормальные формы строятся на основании операций
конъюнкции, дизъюнкции и отрицания, причем отрицание только единственной
переменной.
Определение: Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция
(дизъюнкция) конечного числа попарно различимых переменных или их отрицаний.
Элементарную конъюнкцию (дизъюнкцию) принято называть конъюнктивным
(дизъюнктивным) термом.
В частном случае терм, как конъюнктивный так и дизъюнктивный может состоять
из единственной буквы (литерала). Под буквой будем понимать аргумент Булевой
функции и его отрицания.
Примеры конъюнктивных термов:
_ _
x1, x2, x1x3, x2x4x5 (терм)
___ _
x1x2, x1x2x3 (не терм)
Рангом терма называется количество букв входящих в него.
Дизъюнктивной (конъюнктивной) нормальной формой Булевой функции называется
дизъюнкция (конъюнкция) конечного числа попарно различимых конъюнктивных
(дизъюнктивных) термов.
Каноническая нормальная форма.
Конституентой единицы (нуля) называется конъюнктивный (дизъюнктивный) терм
максимального ранга. Т.е. для Булевой функции от n переменных конституента
включает в себя n букв.
Свойство конституенты: Конституента единицы (нуля) принимает значение единицы
(нуля) на одном и только одном наборе аргументов.
Пример: _ _
n=4 x1x2x3x4 (1010)=1
_ _ _
x1Úx2Úx3Úx4=0
Определение: Дизъюнктивная (конъюнктивная) нормальная форма называется
канонической, если все ее дизъюнктивные (конъюнктивные) термы представляют
собой конституенты единицы (нуля). Иногда канонические формы называют
совершенными.
Пример получения канонических форм:
y=x1Åx2
x1 | x2 | y | Конституента единицы | Конституенты нуля | | 0 | 0 | 0 | - | x1Úx2 | | 0 | 1 | 1 | 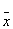 1x2 1x2
| - | | 1 | 0 | 1 | x1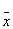 2 2 | - | | 1 | 1 | 0 | - | 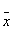 1Ú 1Ú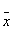 2 2
|
КДНФ - каноническая дизъюнктивная нормальная форма:
_ _
y=x1x2Úx1x2
ККНФ - каноническая конъюнктивная нормальная форма:
_ _
y=(x1Úx2)(x1Úx2)
1) С помощью канонических форм наиболее просто осуществляется переход от
табличной формы задания Булевой функции к аналитической.
2) С помощью канонических форм можно осуществить преобразование любой функции
в Булев базис.
3) Любая Булева функция за исключением логического нуля и логической единицы
имеет единственные КДНФ и ККНФ. Логическую единицу можно представить в виде
КДНФ и логический ноль в виде ККНФ.
4) Правило перехода от табличной формы задания Булевой функции к аналитической:
а) в таблице истинности выделяются все наборы аргументов, при которых функция
равна единице (нулю).
б) для каждого из этих наборов составляют конституенты единицы (нуля).
в) объединением конституенты единицы (нуля) знаками дизъюнкции (конъюнкции)
получается аналитическая форма в виде КДНФ (ККНФ).
Пояснение: при составлении конституент единицы (нуля) используют следующее
правило:
Если некоторый аргумент принимает на наборе значение равное нулю, то в
конституенту единицы он входит с отрицанием, а в конституенту нуля без него.
5) КДНФ и ККНФ представляют собой две различные, но эквивалентные
аналитические формы булевой функции. Это означает, что из одной формы можно
получить другую, используя законы Булевой алгебры.
_ _ _ _ _ _ _ _ _ _
y=(x1Úx2)(x1Úx2)=x1x1Úx1x2Úx2x1Úx2x2=x1x2Úx2x1=x1x2Úx1x2 (КДНФ)
6) Принципиально существует другой способ получения ККНФ:
а) составляется КДНФ, но не для самой, а для ее отрицания.
б) берется отрицание над полученной КДНФ, которое снимается с применением
закона двойственности.
_ _ _ = ------------ ----- ---- _ _
y=x1x2Úx1x2, y=y=x1x2Úx1x2=x1x2 x1x2=( x1Úx2)(x1Úx2)
Разнообразие двоичных алгебр
В связи с тем, что любую сколь угодно сложную Булеву функцию можно
представить в канонических формах, то есть записать ее с помощью операций
отрицания, конъюнкции и дизъюнкции эта система Булевых операций обладает
свойством функциональной полноты, т.е. образует так называемый базис.
Естественно предположить, что система Булевых операций является не
единственной, с помощью которой можно образовать некоторый базис.
В принципе любую из базовых функций можно отождествить соответствующей операцией
и на основе совокупности этих операций построить двоичные алгебры, отличные от
Булевой. К наиболее распространенным двоичным алгебрам относятся: алгебра
Жигалкина (Å, &); алгебра Вебба (Пирса) (¯); алгебра Шеффера ( |
). В каждой из этих алгебр действуют собственные законы. Естественно существуют
взаимно однозначные переходы от операций одного базиса к операциям другого.
Числовое представление Булевых функций
Для любой Булевой функции можно предложить две числовые формы, основанные на
перечислении десятичных эквивалентов наборов аргументов на которых функция
принимает значение единицы (нуля).
f3(x)=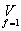 (0,2,6,7) - от этой числовой формы легко перейти к КДНФ путем замены каждого из
наборов в перечислении конституенты единицы.
_ _ _ _ _ _ _ _ _ _ _
y=x1x2x3Úx1x2x3Úx1x2x3Úx1x2x3=x1x3(x2Úx2)Úx1x2(x3Úx3)=x1x3Úx1x2 (ДНФ)
f3(x)=
(0,2,6,7) - от этой числовой формы легко перейти к КДНФ путем замены каждого из
наборов в перечислении конституенты единицы.
_ _ _ _ _ _ _ _ _ _ _
y=x1x2x3Úx1x2x3Úx1x2x3Úx1x2x3=x1x3(x2Úx2)Úx1x2(x3Úx3)=x1x3Úx1x2 (ДНФ)
f3(x)=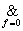 &(1,3,4,5)
_ _ _ _ _ _
y=(x1Úx2Úx3) (x1Úx2Úx3) (x1Úx2Úx3) (x1Úx2Úx3) (*)
Преобразование произвольной аналитической формы Булевой функции в нормальную
В Булевой алгебре в виде теоремы доказывается следующее утверждение:
существует единый конструктивный подход, позволяющий преобразовать
аналитическое выражение Булевой алгебры в произвольной форме к нормальной
форме.
Пример:
_ _ _ _ _ _
y=f4(x)=(x1x2Úx2x3)(x1|x4)=(x1x2Úx2x3)(x1x4)=(x1x2Úx2x3)(x1Úx4)=
_ _ _ _ _ _ _ _ _ _
=x1x2Úx1x2x4Úx1x2x3Úx2x3x4=x1x2Úx1x2x3Úx2x3x4=x1(x2Úx2x3)Úx2x3x4=
_ _ _ _
=x1(x2Úx3) Úx2x3x4=x1x2Úx1x3Úx2x3x4 (КДНФ)
Замечания:
1) В общем случае любая Булева функция может иметь несколько КДНФ,
отличающихся либо количеством термов, либо количеством букв в этих термах.
2) При построении комбинационной схемы, реализующей данную функцию по ее
нормальной форме предпочтительней та, которая обладает наименьшим числом
термов и наименьшим количеством букв в этих термах.
3) По сравнению со схемой, построенной по ДНФ, схема, построенная по
скобочной форме (*), является более предпочтительной т.к. при одном и том же
числе логических элементов (И, ИЛИ) содержат меньшее число входов (9 вместо
10).
Задача преобразования нормальной формы Булевой функции в скобочной форме
называют задачей фактеризации.
4) Сущность конструктивного подхода при получении ДНФ состоит в следуюшем:
а) преобразование операций не-Булевого базиса к операциям Булевого базиса
(см. последние строки таблицы)
б) снятие отрицаний над выражениями с применением законов двойственности
в) раскрытие скобок с применением дистрибутивного закона
г) упрощения выражения с применением закона поглощения
Приведение произвольных нормальных форм Булевой функции к каноническим
Для приведения произвольной ДНФ к КНФ необходимо использовать правило
дизъюнктивного развертывания применительно к каждому из неполных
конъюнктивных термов.
_ _
P=P(xiÚxi)=PxiÚPxi, где P-неполный конъюнктивный терм (ранг этого терма
меньше n), а xi - недостающий в терме аргумент.
Пример:
_ _ _ _ _ _ _
_ _ _
y=x1Úx2x3(ДНФ)=x1(x2Úx2)(x3Úx3) Úx2x3(x1Úx1)=x1x2x3Ú x1x2x3Ú &(1,3,4,5)
_ _ _ _ _ _
y=(x1Úx2Úx3) (x1Úx2Úx3) (x1Úx2Úx3) (x1Úx2Úx3) (*)
Преобразование произвольной аналитической формы Булевой функции в нормальную
В Булевой алгебре в виде теоремы доказывается следующее утверждение:
существует единый конструктивный подход, позволяющий преобразовать
аналитическое выражение Булевой алгебры в произвольной форме к нормальной
форме.
Пример:
_ _ _ _ _ _
y=f4(x)=(x1x2Úx2x3)(x1|x4)=(x1x2Úx2x3)(x1x4)=(x1x2Úx2x3)(x1Úx4)=
_ _ _ _ _ _ _ _ _ _
=x1x2Úx1x2x4Úx1x2x3Úx2x3x4=x1x2Úx1x2x3Úx2x3x4=x1(x2Úx2x3)Úx2x3x4=
_ _ _ _
=x1(x2Úx3) Úx2x3x4=x1x2Úx1x3Úx2x3x4 (КДНФ)
Замечания:
1) В общем случае любая Булева функция может иметь несколько КДНФ,
отличающихся либо количеством термов, либо количеством букв в этих термах.
2) При построении комбинационной схемы, реализующей данную функцию по ее
нормальной форме предпочтительней та, которая обладает наименьшим числом
термов и наименьшим количеством букв в этих термах.
3) По сравнению со схемой, построенной по ДНФ, схема, построенная по
скобочной форме (*), является более предпочтительной т.к. при одном и том же
числе логических элементов (И, ИЛИ) содержат меньшее число входов (9 вместо
10).
Задача преобразования нормальной формы Булевой функции в скобочной форме
называют задачей фактеризации.
4) Сущность конструктивного подхода при получении ДНФ состоит в следуюшем:
а) преобразование операций не-Булевого базиса к операциям Булевого базиса
(см. последние строки таблицы)
б) снятие отрицаний над выражениями с применением законов двойственности
в) раскрытие скобок с применением дистрибутивного закона
г) упрощения выражения с применением закона поглощения
Приведение произвольных нормальных форм Булевой функции к каноническим
Для приведения произвольной ДНФ к КНФ необходимо использовать правило
дизъюнктивного развертывания применительно к каждому из неполных
конъюнктивных термов.
_ _
P=P(xiÚxi)=PxiÚPxi, где P-неполный конъюнктивный терм (ранг этого терма
меньше n), а xi - недостающий в терме аргумент.
Пример:
_ _ _ _ _ _ _
_ _ _
y=x1Úx2x3(ДНФ)=x1(x2Úx2)(x3Úx3) Úx2x3(x1Úx1)=x1x2x3Ú x1x2x3Ú
 _ _ _ _ _ _ _ _ _
Úx1x2x3Úx1x2x3Ú x1x2x3Ú x1x2x3 (КДНФ)
Замечание:
После раскрытия скобок могут получиться одинаковые термы, из которых нужно
оставить только один.
y= _ _ _ _ _ _ _ _ _
Úx1x2x3Úx1x2x3Ú x1x2x3Ú x1x2x3 (КДНФ)
Замечание:
После раскрытия скобок могут получиться одинаковые термы, из которых нужно
оставить только один.
y=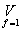 (0,1,2,3,5)=f3
Преобразование КНФ к ККНФ реализуется путем применения правила конъюнктивного
развертывания к каждому неполному дизъюнктивному терму.
_ _
P=PÚxixi=(PÚxi)(PÚxi)
_ _ _ _ _ _ _ _ _
_
y=x1Úx2x3(ДНФ)=(x1Úx2)(x1Úx3)(КНФ)=(x1Úx2Úx3x3)(x1Úx3Úx2x2)= (0,1,2,3,5)=f3
Преобразование КНФ к ККНФ реализуется путем применения правила конъюнктивного
развертывания к каждому неполному дизъюнктивному терму.
_ _
P=PÚxixi=(PÚxi)(PÚxi)
_ _ _ _ _ _ _ _ _
_
y=x1Úx2x3(ДНФ)=(x1Úx2)(x1Úx3)(КНФ)=(x1Úx2Úx3x3)(x1Úx3Úx2x2)=
 _ _ _ _ _ _ _ _
=(x1Úx2Úx3)(x1Úx2Úx3)(x1Úx2Úx3)(x1Úx2Úx3)(ККНФ)
y= _ _ _ _ _ _ _ _
=(x1Úx2Úx3)(x1Úx2Úx3)(x1Úx2Úx3)(x1Úx2Úx3)(ККНФ)
y=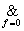 (4,6,7)
Минимизация булевых функций на картах Карно(см. Практику).
Метод Квайна-МакКласски базируется на кубическом представлении булевых функций.
Кубическое представление булевых функций.
В кубическом представлении булевой функции от n переменных все множество из 2
n наборов ее аргументов рассматривается как множество координат вершин
n-мерного куба с длинной ребра равной 1. В соответствии с этим наборы
аргументов, на которых булева функция принимает значение равное 1 принято
называть существенными вершинами.
Существенные вершины образуют так называемые ноль-кубы (0-кубы). Между 0-
кубами существует отношение соседства и определена операция склеивания. Два
0-куба называются соседними если они отличаются только по одной координате.
Пример : n=4 0101
0001 - два соседних 0-куба
результат склеивания : 0x01 (*)
Склеивание 2-х соседних 0-кубов дает в результате 1-куб. Координата,
отмечаемая символом х, называется свободной (независимой, несвязанной), а
остальные (числовые) координаты называются зависимыми (связанными).
Аналогичное отношение соседства существует между 1-кубами, в результате
склеивания которых получается 2-куб.
0х01
0х11 - 0хх1 (**)
В продолжении аналогии два r-куба называются соседними если они отличаются
только по одной (естественно зависимой) координате. r-куб содержит r
независимых и n-r зависимых координат. В результате склеивания 2-х соседних
r-кубов образуется (r+1)-куб содержащий r+1 независимую координату.
Операция склеивания над кубами соответствует применению закона склеивания к
конъюнктивным термам, отождествляемым с этими кубами.
Пример : для склеивания (*)
_ _ _ _ _ _ _
х1х2х3х4Ú х1х2х3х4= х1х3х4
(0101) (0001) (0х01)
_ _ _ _
для (**) х1х3х4Ú х1х3х4= х1х4
(0х01) (0х11) (0хх1)
Определения.
Кубическим комплексом K0(f) булевой функции f называется множество
0-кубов этой функции. В общем случае кубическим комплексом Kr(f)
булевой функции f называется объеденение множеств кубов всех размерностей этой
функции
m
k(f)=UKr(f) m-максимальная размерность кубов функции f.
r=0
Пример получения кубических комплексов
f3(x)=V(1,2,3,6,7) |001 (1) |0x1 (1-3) (1)
(f=1) |010 (2) |01x (2-3) (2)
K0(f)=|011 (3) K1(f)=|x10 (2-4) (3) K2(f)=|x1x (2-5)
|110 (4) |x11 (3-5) (4)
|111 (5) |11x (4-5) (5)
K3(f)=пустому множеству
K(f)=K0(f)UK1(f)UK2(f)
Для получения кубического комплекса K(f) необходимо провести всевозможные
операции склеивания над 0-кубами, 1-кубами и т.д. до тех пор пока на очередном
шаге не получится Kr+1(f)=пустому множеству. При склеивании 1-кубов
2-кубы представлены в 2-х экземплярах как результаты склеивания 2-х различных
пар 1-кубов.
Распространяя этот принцип можно утверждать, что r-кубы как результат
склеивания (r-1)-кубов получаются в r-кратном количестве экземпляров.
Куб, входящий в состав кубического комплекса K(f) называется максимальным,
если он не вступает ни в одну операцию склеивания.
В приведенном примере максимальными кубами являются х1х и 0х17.
Геометрическая интерпретация кубов малой размерности. Графическое
представление булевых функций.
Подобный подход носит ограниченный характер и как правило является наглядным
для булевых функций от 2-х и 3-х переменных.
F3(x)=V(1,2,3,6,7)
(f=1) (4,6,7)
Минимизация булевых функций на картах Карно(см. Практику).
Метод Квайна-МакКласски базируется на кубическом представлении булевых функций.
Кубическое представление булевых функций.
В кубическом представлении булевой функции от n переменных все множество из 2
n наборов ее аргументов рассматривается как множество координат вершин
n-мерного куба с длинной ребра равной 1. В соответствии с этим наборы
аргументов, на которых булева функция принимает значение равное 1 принято
называть существенными вершинами.
Существенные вершины образуют так называемые ноль-кубы (0-кубы). Между 0-
кубами существует отношение соседства и определена операция склеивания. Два
0-куба называются соседними если они отличаются только по одной координате.
Пример : n=4 0101
0001 - два соседних 0-куба
результат склеивания : 0x01 (*)
Склеивание 2-х соседних 0-кубов дает в результате 1-куб. Координата,
отмечаемая символом х, называется свободной (независимой, несвязанной), а
остальные (числовые) координаты называются зависимыми (связанными).
Аналогичное отношение соседства существует между 1-кубами, в результате
склеивания которых получается 2-куб.
0х01
0х11 - 0хх1 (**)
В продолжении аналогии два r-куба называются соседними если они отличаются
только по одной (естественно зависимой) координате. r-куб содержит r
независимых и n-r зависимых координат. В результате склеивания 2-х соседних
r-кубов образуется (r+1)-куб содержащий r+1 независимую координату.
Операция склеивания над кубами соответствует применению закона склеивания к
конъюнктивным термам, отождествляемым с этими кубами.
Пример : для склеивания (*)
_ _ _ _ _ _ _
х1х2х3х4Ú х1х2х3х4= х1х3х4
(0101) (0001) (0х01)
_ _ _ _
для (**) х1х3х4Ú х1х3х4= х1х4
(0х01) (0х11) (0хх1)
Определения.
Кубическим комплексом K0(f) булевой функции f называется множество
0-кубов этой функции. В общем случае кубическим комплексом Kr(f)
булевой функции f называется объеденение множеств кубов всех размерностей этой
функции
m
k(f)=UKr(f) m-максимальная размерность кубов функции f.
r=0
Пример получения кубических комплексов
f3(x)=V(1,2,3,6,7) |001 (1) |0x1 (1-3) (1)
(f=1) |010 (2) |01x (2-3) (2)
K0(f)=|011 (3) K1(f)=|x10 (2-4) (3) K2(f)=|x1x (2-5)
|110 (4) |x11 (3-5) (4)
|111 (5) |11x (4-5) (5)
K3(f)=пустому множеству
K(f)=K0(f)UK1(f)UK2(f)
Для получения кубического комплекса K(f) необходимо провести всевозможные
операции склеивания над 0-кубами, 1-кубами и т.д. до тех пор пока на очередном
шаге не получится Kr+1(f)=пустому множеству. При склеивании 1-кубов
2-кубы представлены в 2-х экземплярах как результаты склеивания 2-х различных
пар 1-кубов.
Распространяя этот принцип можно утверждать, что r-кубы как результат
склеивания (r-1)-кубов получаются в r-кратном количестве экземпляров.
Куб, входящий в состав кубического комплекса K(f) называется максимальным,
если он не вступает ни в одну операцию склеивания.
В приведенном примере максимальными кубами являются х1х и 0х17.
Геометрическая интерпретация кубов малой размерности. Графическое
представление булевых функций.
Подобный подход носит ограниченный характер и как правило является наглядным
для булевых функций от 2-х и 3-х переменных.
F3(x)=V(1,2,3,6,7)
(f=1)
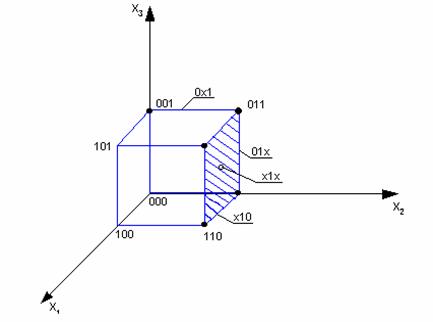 Геометрическим местом 0-куба является точка, представляющая существенную
вершину.
Два соседних 0-куба являются концами какого-либо ребра.
Геометрическим местом 1-куба является ребро, замыкаемое склеивающимися 0-
кубами, образующими данный 1-куб.
Два параллельных ребра, образующих грань, являются образами склеивающихся 1-
кубов. В соответствии с этим геометрической интерпретацией 2-куба является
грань, образуемая парой параллельных ребер. Так как любую грань можно
определить одной из пар параллельных ребер, 2-куб может быть получен как
результат склеивания двух различных пар 1-кубов, то есть представляется в
двух экземплярах.
Геометрическим образом 3-куба можно считать 3-х мерный куб. Так как он может
быть образован 3-мя способами как пара параллельных граней, то при склеивании
он получается в трех экземплярах.
Покрытия булевых функций.
Между кубами различной размерности, входящих в кубический комплекс K(f),
существует отношение включения или покрытия. Принято говорить, что куб А
меньшей размерности покрывается кубом Б большей размерности, если куб А
включается в куб Б. Это означает, что при образовании куба Б хотя бы в одном
склеивании учавствует куб А.
Отношение включения (покрытия) между кубами принято обозначать АÌБ. В
теории множеств отношение включения связывает между собой некоторое множество
и его подмножества.
Для рассмотренного примера отношения включения имеют место между
001Ì0х1; 011Ìx11Ìx1x... любой 1-куб покрывает 2 0-куба,
2-куб - 4 0-куба и 2 1-куба, 3-куб покрывает 8 0-кубов, 12 1-кубов и 6 2-
кубов.
Покрытием булевой функции f называется такое подмножество кубов из
кубического комплекса K(f), которое покрывает все существенные вершины
функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие
конъюнктивный терм, для любого покрытия можно представить некоторую ДНФ
булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K0
(f), покрытие c0(f)=K0(f). Этому покрытию соответствует
КДНФ.
Для примера покрытием является также
|0x1
|01x
c1(f)=K1(f)=|x10
|x11
|11x
этому покрытию соответствует ДНФ вида
_ _ _ _ _ _ _ _ _ _
f=x1x3vx1x2vx2x3vx2x3vx1x2 приведенная ДНФ не является минимальной.
В качестве минимальной еще одного покрытия можно использовать множество
максимальных кубов
|0x1
c2(f)=|x1x
Действительно, куб 0х1 покрывает существенные вершины 0х1É(001, 011),
а куб x1xÉ(010, 011, 110, 111).
Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытие c2(f) соответствует ДНФ вида х1х3vx
2. Эта ДНФ является минимальной. Покрытие булевой функции, которое
соответствует минимальной ДНФ называется минимальным покрытием.
Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае все множество максимальных кубов является минимальным
покрытием. Это справедливо для нашего примера. В общем случае множество
максимальных кубов является избыточным и для получения минимального покрытия
достаточно взять некоторое его подмножество.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
|000 (1) |00x (1-2)
|001 (2) |x00 (1-3)
K0(f)=|100 (3) K1(f)=|1x0 (3-4)
|110 (4) |11x (4-5)
|111 (5)
Для данного примера множество максимальных кубов совпадает с комплексом K1
(f). Z(f)=K1(f)
Минимальными покрытиями являются
|00x |00x
с1(f)=|11x c2(f)=|11x
|x00 |1x0
Из анализа покрытия существенных вершин максимальными кубами из комплекса K
1(f) следует :
1) Куб 00х должен обязательно включаться в покрытие, так как только он
покрывает существенную вершину 001, аналогично 11х покрывает 111.
Множество максимальных кубов без которых не может быть образовано покрытие
булевой функции называется ядром покрытия T(f)=|00x
|11x
2) Так как ядром покрытия кроме существенных вершин 001 и 111 покрываются
также существенные вершины 000 и 110, то не покрытой ядром остается только
существенная вершина 100. Для ее покрытия достаточно взять 1 из оставшихся
максимальных кубов (х00 или 1х0).
Выводы :
Задача получения минимальной ДНФ сводится к задаче получения минимального
покрытия.
Получение минимального покрытия реализуется в таком порядке : а) Находится
множество максимальных кубов б) Выделяется ядро покрытия в) Из максимальных
кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое
покрывает существенные вершины, не покрытые ядром.
Цена покрытия.
Цена r-куба представляет собой количество несвязанных координат. Sr=n*r
Для оценки качества покрытия используют два вида цены покрытия :
m
1) Sa=åSrNr, где Nr - количество r-кубов, входящих в по-
r=0
крытие, m - максимальная размерность куба. Цена Sa представляет
собой сумму цен кубов, входящих в покрытие.
2) Sb=Sa+k, где k - количество кубов, входящих в покрытие
m m
Sa =å(n-r) Nr ; Sb=å(n-r)(Nr+1)
r=0 r=0
Под минимальным покрытием понимают покрытие, обладающее минимальной ценой S
a по сравнению с любым другим покрытием этой функции.
Можно показать, что покрытие, обладающее минимальной ценой Sa
обладает также и минимальной ценой Sb.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
C0(f)=K0(f) ; Sa=5*3=15 ; Sb=Sa+5=20
C1(f)=K1(f) ; Sa=4*2=8 ; Sb=Sa+4=12
Cmin(f) : Sa=3*2=6 ; Sb=9
Цена покрытия Sa представляет собой количество букв, входящих в ДНФ,
которая соответствует данному покрытию.
Цена Sb представляет для ДНФ сумму количества букв и количества термов.
Геометрическим местом 0-куба является точка, представляющая существенную
вершину.
Два соседних 0-куба являются концами какого-либо ребра.
Геометрическим местом 1-куба является ребро, замыкаемое склеивающимися 0-
кубами, образующими данный 1-куб.
Два параллельных ребра, образующих грань, являются образами склеивающихся 1-
кубов. В соответствии с этим геометрической интерпретацией 2-куба является
грань, образуемая парой параллельных ребер. Так как любую грань можно
определить одной из пар параллельных ребер, 2-куб может быть получен как
результат склеивания двух различных пар 1-кубов, то есть представляется в
двух экземплярах.
Геометрическим образом 3-куба можно считать 3-х мерный куб. Так как он может
быть образован 3-мя способами как пара параллельных граней, то при склеивании
он получается в трех экземплярах.
Покрытия булевых функций.
Между кубами различной размерности, входящих в кубический комплекс K(f),
существует отношение включения или покрытия. Принято говорить, что куб А
меньшей размерности покрывается кубом Б большей размерности, если куб А
включается в куб Б. Это означает, что при образовании куба Б хотя бы в одном
склеивании учавствует куб А.
Отношение включения (покрытия) между кубами принято обозначать АÌБ. В
теории множеств отношение включения связывает между собой некоторое множество
и его подмножества.
Для рассмотренного примера отношения включения имеют место между
001Ì0х1; 011Ìx11Ìx1x... любой 1-куб покрывает 2 0-куба,
2-куб - 4 0-куба и 2 1-куба, 3-куб покрывает 8 0-кубов, 12 1-кубов и 6 2-
кубов.
Покрытием булевой функции f называется такое подмножество кубов из
кубического комплекса K(f), которое покрывает все существенные вершины
функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие
конъюнктивный терм, для любого покрытия можно представить некоторую ДНФ
булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K0
(f), покрытие c0(f)=K0(f). Этому покрытию соответствует
КДНФ.
Для примера покрытием является также
|0x1
|01x
c1(f)=K1(f)=|x10
|x11
|11x
этому покрытию соответствует ДНФ вида
_ _ _ _ _ _ _ _ _ _
f=x1x3vx1x2vx2x3vx2x3vx1x2 приведенная ДНФ не является минимальной.
В качестве минимальной еще одного покрытия можно использовать множество
максимальных кубов
|0x1
c2(f)=|x1x
Действительно, куб 0х1 покрывает существенные вершины 0х1É(001, 011),
а куб x1xÉ(010, 011, 110, 111).
Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытие c2(f) соответствует ДНФ вида х1х3vx
2. Эта ДНФ является минимальной. Покрытие булевой функции, которое
соответствует минимальной ДНФ называется минимальным покрытием.
Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае все множество максимальных кубов является минимальным
покрытием. Это справедливо для нашего примера. В общем случае множество
максимальных кубов является избыточным и для получения минимального покрытия
достаточно взять некоторое его подмножество.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
|000 (1) |00x (1-2)
|001 (2) |x00 (1-3)
K0(f)=|100 (3) K1(f)=|1x0 (3-4)
|110 (4) |11x (4-5)
|111 (5)
Для данного примера множество максимальных кубов совпадает с комплексом K1
(f). Z(f)=K1(f)
Минимальными покрытиями являются
|00x |00x
с1(f)=|11x c2(f)=|11x
|x00 |1x0
Из анализа покрытия существенных вершин максимальными кубами из комплекса K
1(f) следует :
1) Куб 00х должен обязательно включаться в покрытие, так как только он
покрывает существенную вершину 001, аналогично 11х покрывает 111.
Множество максимальных кубов без которых не может быть образовано покрытие
булевой функции называется ядром покрытия T(f)=|00x
|11x
2) Так как ядром покрытия кроме существенных вершин 001 и 111 покрываются
также существенные вершины 000 и 110, то не покрытой ядром остается только
существенная вершина 100. Для ее покрытия достаточно взять 1 из оставшихся
максимальных кубов (х00 или 1х0).
Выводы :
Задача получения минимальной ДНФ сводится к задаче получения минимального
покрытия.
Получение минимального покрытия реализуется в таком порядке : а) Находится
множество максимальных кубов б) Выделяется ядро покрытия в) Из максимальных
кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое
покрывает существенные вершины, не покрытые ядром.
Цена покрытия.
Цена r-куба представляет собой количество несвязанных координат. Sr=n*r
Для оценки качества покрытия используют два вида цены покрытия :
m
1) Sa=åSrNr, где Nr - количество r-кубов, входящих в по-
r=0
крытие, m - максимальная размерность куба. Цена Sa представляет
собой сумму цен кубов, входящих в покрытие.
2) Sb=Sa+k, где k - количество кубов, входящих в покрытие
m m
Sa =å(n-r) Nr ; Sb=å(n-r)(Nr+1)
r=0 r=0
Под минимальным покрытием понимают покрытие, обладающее минимальной ценой S
a по сравнению с любым другим покрытием этой функции.
Можно показать, что покрытие, обладающее минимальной ценой Sa
обладает также и минимальной ценой Sb.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
C0(f)=K0(f) ; Sa=5*3=15 ; Sb=Sa+5=20
C1(f)=K1(f) ; Sa=4*2=8 ; Sb=Sa+4=12
Cmin(f) : Sa=3*2=6 ; Sb=9
Цена покрытия Sa представляет собой количество букв, входящих в ДНФ,
которая соответствует данному покрытию.
Цена Sb представляет для ДНФ сумму количества букв и количества термов.
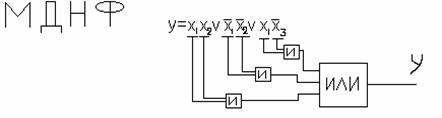 Цена покрытия хорошо согласуется с ценой схемы по Квайну, которая строится по
нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ=9=Sb (9-число входов).
В принципе, между SQ и ценами Sa и Sb
существует соотношение Sa £ SQ £ Sb
Это неравенство имеет место при следующих допущениях по комбинационной схеме :
1) Схема строится по нормальной форме (ДНФ или КНФ).
2) Схема строится на элементах булевого базиса (И, ИЛИ).
3) На входы схемы можно подавать как прямые, так и инверсные значения входных
переменных, представляющие собой значения аргументов булевой функции (схема с
парафазными входами). Элементы НЕ (инвертора в схеме отсутствуют.
Нулевое покрытие булевой функции и получение минимальной КНФ.
Выше было рассмотрено покрытие булевой функции на наборах аргументов для
которых функция равна единице.
Такие покрытия можно назвать единичными. Наряду с единичными покрытиями
существуют и нулевые, для которых покрываются наборы аргументов, на которых
функция равна нулю, то есть покрытие реализуется для существенных вершин, но
не самой функции, а ее отрицания (инверсии).
Нулевое покрытие строится также как и единичное, но только для отрицания
исходной функции.
f3(x)=V(0,1,4,6,7) f3(x)=&(2,3,5)
(f=1) (f=0) _ |010
K0( f )=|011
_ _ |101
C0( f )= K0( f ) Sa=9 Sb=12
_ _ _
K1( f )=|01x Z( f )=Cmin( f )=|01x Sa=5 Sb=7
|101
Цена минимального нулевого покрытия оказалась меньше цены минимального
единичного покрытия.
Так как заранее предсказать невозможно, какое из минимальных покрытий данной
функции, единичное или нулевое, будет иметь меньшую цену, то для построения
схемы, обладающей минимальной ценой по Квайну, целесообразно решать задачу
минимзации в отношении обоих покрытий.
Импликанты булевой функции.
Системы импликант.
Решение задачи минимизации булевой функции методом Квайна и
усовершенствованным методом Квайна-МакКласски базируется на понятиях
импликант и их систем.
Определение : Булева функция g(x) называется импликантой булевой функции
f(x), если для любого набора аргументов, на которых g(x)=1, f(x) также равна
единице.
~ ~ ~
g( x )=1 => f( x )=1, где х - некоторый набор аргументов.
Свойства импликант :
1) Между импликантой и самой функцией существует отношение включения
g(x)Ìf(x).
2) Можно утверждать, что для любого набора аргументов, на котором функция
равна нулю, ее импликанта также равна нулю.
3) Если g(x) и j(x) являются импликантами функции f(x), то их дизъюнкция
также является импликантой этой функции.
Простейшими примерами импликант могут служить конъюнктивные термы, входящие в
ДНФ данной функции.
Пример : для f3(x)=V(0,1,4,6,7) (#)
(f=1) _ _ _
импликантами являются х1х2х3; х1х2х3; х1х2;...
Произвольная дизъюнкция этих термов также является импликантой функции.
Определение : Простой (первичной) импликантой булевой функции называется
конъюнктивный терм, который сам является импликантой этой функции, но никакая
его собственная часть уже не является импликантой этой функции.
Под собственной частью терма понимается новый терм, полученный из исходного,
путем вычеркивания произвольного числа букв.
Для данного примера функции (#) простыми импликантами являются :
_ _ _
х1х2х3; х1х2х3; х1х2;...
Множеству простых импликант можно поставить в соответствие множество
максимальных кубов.
Определение : Дизъюнкция всех простых импликант булевой функции представляет
собой ДНФ этой функции, которая называется сокращенной - СДНФ.
Для функции (#) из приведенного примера
_ _ _ _ _
СДНФ : y= х1х2v х1х2vх2х3v х1х3
Понятие «сокращенное» присвоено ДНФ в том смысле, что она, как правило,
содержит меньшее количество букв и термов по сравнению с КДНФ. Для нашего
примера КДНФ содержит 15 букв и 5 термов, а СДНФ - 8 букв и 4 терма.
Аналогия между импликантами и кубическим представлением Булевой функции
Любому кубу из К(f) можно поставить в соответствие конъюнктивный терм который
можно рассматривать как импликанту булевой функции .Любой простой импликанте
булевой функции соответствует максимальный куб ,и в свою очередь множество
всех простых импликант соответствует множеству Z(f) всех максимальных кубов
К(f).
Таким образом можно провести некоторую аналогию между сокращенной СДНФ и Z(f).
В отношении импликант булевой функции также как и в отношении кубов
соответствующих им существует отношение покрытия.
Принято считать ,что импликанта покрывает некоторую существенную вершину или
в общем случае некоторый куб из К(f) ,если значение импликанты на наборе
аргументов представляющем данную существенную вершину равно 1 или в общем
случае значение импликанты равно 1 для всех существенных вершин покрываемых
кубом из К(f).
ПРИМЕР : импликанта х1х2 покрывает существенные вершины
(110,111) и в свою очередь покрывает куб 11х.
Определение :множество импликант булевой функции образует полную систему
импликант ,если любая существенная вершина булевой функции покрывается хотя
бы одной импликантой этого множества.
Если считать ,что в полную систему импликант включаются импликанты только в
виде конъюнктивных термов и не включает импликанты в виде дизъюнктивных
термов ,то полной системе импликант можно поставить в соответствие некоторое
множество кубов из К(f) образующих покрытие булевой функции f .
Так например ,кубам из кубического комплекса К°(f) соответствует полная
система импликант ,представляющая собой множество конституент 1 данной
функции f. В свою очередь множеству максимальных кубов Z(f) ,естественно
образующих покрытие булевой функции ,соответствует полная система простых
импликант.
Определение :система простых импликант называется приведенной ,если она
является полной ,а никакая ее собственная часть уже не образует полную
систему импликант.
Для функции y= x 1 x 2 Ú
Цена покрытия хорошо согласуется с ценой схемы по Квайну, которая строится по
нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ=9=Sb (9-число входов).
В принципе, между SQ и ценами Sa и Sb
существует соотношение Sa £ SQ £ Sb
Это неравенство имеет место при следующих допущениях по комбинационной схеме :
1) Схема строится по нормальной форме (ДНФ или КНФ).
2) Схема строится на элементах булевого базиса (И, ИЛИ).
3) На входы схемы можно подавать как прямые, так и инверсные значения входных
переменных, представляющие собой значения аргументов булевой функции (схема с
парафазными входами). Элементы НЕ (инвертора в схеме отсутствуют.
Нулевое покрытие булевой функции и получение минимальной КНФ.
Выше было рассмотрено покрытие булевой функции на наборах аргументов для
которых функция равна единице.
Такие покрытия можно назвать единичными. Наряду с единичными покрытиями
существуют и нулевые, для которых покрываются наборы аргументов, на которых
функция равна нулю, то есть покрытие реализуется для существенных вершин, но
не самой функции, а ее отрицания (инверсии).
Нулевое покрытие строится также как и единичное, но только для отрицания
исходной функции.
f3(x)=V(0,1,4,6,7) f3(x)=&(2,3,5)
(f=1) (f=0) _ |010
K0( f )=|011
_ _ |101
C0( f )= K0( f ) Sa=9 Sb=12
_ _ _
K1( f )=|01x Z( f )=Cmin( f )=|01x Sa=5 Sb=7
|101
Цена минимального нулевого покрытия оказалась меньше цены минимального
единичного покрытия.
Так как заранее предсказать невозможно, какое из минимальных покрытий данной
функции, единичное или нулевое, будет иметь меньшую цену, то для построения
схемы, обладающей минимальной ценой по Квайну, целесообразно решать задачу
минимзации в отношении обоих покрытий.
Импликанты булевой функции.
Системы импликант.
Решение задачи минимизации булевой функции методом Квайна и
усовершенствованным методом Квайна-МакКласски базируется на понятиях
импликант и их систем.
Определение : Булева функция g(x) называется импликантой булевой функции
f(x), если для любого набора аргументов, на которых g(x)=1, f(x) также равна
единице.
~ ~ ~
g( x )=1 => f( x )=1, где х - некоторый набор аргументов.
Свойства импликант :
1) Между импликантой и самой функцией существует отношение включения
g(x)Ìf(x).
2) Можно утверждать, что для любого набора аргументов, на котором функция
равна нулю, ее импликанта также равна нулю.
3) Если g(x) и j(x) являются импликантами функции f(x), то их дизъюнкция
также является импликантой этой функции.
Простейшими примерами импликант могут служить конъюнктивные термы, входящие в
ДНФ данной функции.
Пример : для f3(x)=V(0,1,4,6,7) (#)
(f=1) _ _ _
импликантами являются х1х2х3; х1х2х3; х1х2;...
Произвольная дизъюнкция этих термов также является импликантой функции.
Определение : Простой (первичной) импликантой булевой функции называется
конъюнктивный терм, который сам является импликантой этой функции, но никакая
его собственная часть уже не является импликантой этой функции.
Под собственной частью терма понимается новый терм, полученный из исходного,
путем вычеркивания произвольного числа букв.
Для данного примера функции (#) простыми импликантами являются :
_ _ _
х1х2х3; х1х2х3; х1х2;...
Множеству простых импликант можно поставить в соответствие множество
максимальных кубов.
Определение : Дизъюнкция всех простых импликант булевой функции представляет
собой ДНФ этой функции, которая называется сокращенной - СДНФ.
Для функции (#) из приведенного примера
_ _ _ _ _
СДНФ : y= х1х2v х1х2vх2х3v х1х3
Понятие «сокращенное» присвоено ДНФ в том смысле, что она, как правило,
содержит меньшее количество букв и термов по сравнению с КДНФ. Для нашего
примера КДНФ содержит 15 букв и 5 термов, а СДНФ - 8 букв и 4 терма.
Аналогия между импликантами и кубическим представлением Булевой функции
Любому кубу из К(f) можно поставить в соответствие конъюнктивный терм который
можно рассматривать как импликанту булевой функции .Любой простой импликанте
булевой функции соответствует максимальный куб ,и в свою очередь множество
всех простых импликант соответствует множеству Z(f) всех максимальных кубов
К(f).
Таким образом можно провести некоторую аналогию между сокращенной СДНФ и Z(f).
В отношении импликант булевой функции также как и в отношении кубов
соответствующих им существует отношение покрытия.
Принято считать ,что импликанта покрывает некоторую существенную вершину или
в общем случае некоторый куб из К(f) ,если значение импликанты на наборе
аргументов представляющем данную существенную вершину равно 1 или в общем
случае значение импликанты равно 1 для всех существенных вершин покрываемых
кубом из К(f).
ПРИМЕР : импликанта х1х2 покрывает существенные вершины
(110,111) и в свою очередь покрывает куб 11х.
Определение :множество импликант булевой функции образует полную систему
импликант ,если любая существенная вершина булевой функции покрывается хотя
бы одной импликантой этого множества.
Если считать ,что в полную систему импликант включаются импликанты только в
виде конъюнктивных термов и не включает импликанты в виде дизъюнктивных
термов ,то полной системе импликант можно поставить в соответствие некоторое
множество кубов из К(f) образующих покрытие булевой функции f .
Так например ,кубам из кубического комплекса К°(f) соответствует полная
система импликант ,представляющая собой множество конституент 1 данной
функции f. В свою очередь множеству максимальных кубов Z(f) ,естественно
образующих покрытие булевой функции ,соответствует полная система простых
импликант.
Определение :система простых импликант называется приведенной ,если она
является полной ,а никакая ее собственная часть уже не образует полную
систему импликант.
Для функции y= x 1 x 2 Ú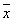 1 1 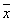 2Ú 2Ú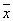 2 2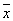 3 Ú x 1 3 Ú x 1 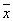 3 (*)
система простых импликант
{ x 1 x 2, 3 (*)
система простых импликант
{ x 1 x 2, 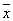 1 1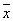 2 , 2 , 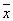 2 2 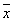 3 , x 1 3 , x 1 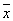 3 }
является полной ,но не является приведенной ,т.к. из нее можно исключить одну из
импликант не нарушая полноты системы .{ 3 }
является полной ,но не является приведенной ,т.к. из нее можно исключить одну из
импликант не нарушая полноты системы .{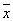 2
2 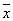 3
или x1 3
или x1 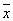 2}
Определение: Дизъюнкция всех простых импликант ,образующих некоторую
приведенную систему называется тупиковой ДНФ булевой функции или ТДНФ
Для функции (*) существуют две ТДНФ
2}
Определение: Дизъюнкция всех простых импликант ,образующих некоторую
приведенную систему называется тупиковой ДНФ булевой функции или ТДНФ
Для функции (*) существуют две ТДНФ
 1) у= x 1 x 2Ú
1) у= x 1 x 2Ú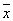 1 1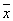 2Ú 2Ú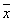 2 2 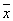 3
2) у= x 1 x 2Ú 3
2) у= x 1 x 2Ú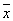 1 1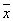 2Ú x 1 2Ú x 1 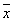 3
В данном случае они совпадaют с минимальной ДНФ. Но в общем случае это
утверждение не справедливо. Т.е. минимальная ДНФ обязательно является ТДНФ но
не любая ТДНФ является МДНФ. Таким образом множество МДНФ является
подмножеством ТДНФ.
Определение: простая импликанта булевой функции называется существенной если
она и только она покрывает некоторую существенную вершину этой функции.
Множество существенных импликант соответствует максимальным кубам образующим
ядро покрытия.
ПОСЛЕДОВАТЕЛЬНОСТЬ действий для решения канонической задачи минимизации
методом Квайна-Мак-Класки.
1)Нахождение множества максимальных кубов или простых импликант функции.
2)Выделение ядра покрытия.
3)Дополнение множества кубов ,принадлежащих ядру покрытия таким минимальным
подмножеством из максимальных кубов ,не входящих в ядро покрытия ,для
получения покрытия с минимальной ценой.
С точки зрения последовательного преобразования ДНФ булевой функции с целью
их упрощения каноническая задача минимизации может быть представлена в виде
КДНФ.
КДНФÞСДНФÞ{ТДНФ}Þ{МДНФ}
Распространение терминологии в отношении нулевого покрытия определяется на
понятии импликанта как соответствие импликанте и на системе импликант.
ПРИМЕР: (минимизация булевой функции методом Квайна-Мак-Класки)
1) f4(x)=V(0,1,5,7,8,10,12,14,15)
(f=1)
f4(x)=&(2,3,4,6,9,11,13)
(f=0)
На этапе получения множества максимальных кубов целесообразно разделить
множество ноль - кубов (К°(f)) на ряд подмножеств ,отличающихся количеством
единиц .
В операцию склеивания в этом случае могут вступать только кубы ,относящиеся к
соседним подмножествам ,то есть отличающиеся на единицу
ì 000X ü
ï X000 ÷ K°(f)=C°(f)
ï 0X01 ÷
Z(f)= í 01X1 ý Sa=36
ê X111 ú Sb=45
ê 111X ú
î 1XX0 þ
K1(f)=C1(f) Sa=10*3=30
Sb=40
Z(f)=C3(f) Sa=20
Sb=27
При минимизации не полностью определенной булевой функции множество
максимальных кубов определяется на объединении множества существенных вершин
и безразличных наборов в целях получения кубов наибольшей размерности .
2) Определение ядра покрытия .
Выполнение этого этапа реализуется с помощью таблицы покрытий .
Kаждая строка таблицы - максимальный куб(простая импликанта).
Каждый столбец - существенная вершина булевой функции (безразличные наборы не
включаются).
Элементы этой таблицы отражают отношение покрытия ,то есть на пересечении i-
ой строки и j-ого столбца ставится некоторая отметка в том случае если i-ый
максимальный куб покрывает j-ую вершину .
Таблицу покрытий иногда называют импликантной таблицей с учетом того ,что
каждый максимальный куб соответствует простой импликанте а существенные
вершины конституантам
единицы(нуля).
Существенные вершины 3
В данном случае они совпадaют с минимальной ДНФ. Но в общем случае это
утверждение не справедливо. Т.е. минимальная ДНФ обязательно является ТДНФ но
не любая ТДНФ является МДНФ. Таким образом множество МДНФ является
подмножеством ТДНФ.
Определение: простая импликанта булевой функции называется существенной если
она и только она покрывает некоторую существенную вершину этой функции.
Множество существенных импликант соответствует максимальным кубам образующим
ядро покрытия.
ПОСЛЕДОВАТЕЛЬНОСТЬ действий для решения канонической задачи минимизации
методом Квайна-Мак-Класки.
1)Нахождение множества максимальных кубов или простых импликант функции.
2)Выделение ядра покрытия.
3)Дополнение множества кубов ,принадлежащих ядру покрытия таким минимальным
подмножеством из максимальных кубов ,не входящих в ядро покрытия ,для
получения покрытия с минимальной ценой.
С точки зрения последовательного преобразования ДНФ булевой функции с целью
их упрощения каноническая задача минимизации может быть представлена в виде
КДНФ.
КДНФÞСДНФÞ{ТДНФ}Þ{МДНФ}
Распространение терминологии в отношении нулевого покрытия определяется на
понятии импликанта как соответствие импликанте и на системе импликант.
ПРИМЕР: (минимизация булевой функции методом Квайна-Мак-Класки)
1) f4(x)=V(0,1,5,7,8,10,12,14,15)
(f=1)
f4(x)=&(2,3,4,6,9,11,13)
(f=0)
На этапе получения множества максимальных кубов целесообразно разделить
множество ноль - кубов (К°(f)) на ряд подмножеств ,отличающихся количеством
единиц .
В операцию склеивания в этом случае могут вступать только кубы ,относящиеся к
соседним подмножествам ,то есть отличающиеся на единицу
ì 000X ü
ï X000 ÷ K°(f)=C°(f)
ï 0X01 ÷
Z(f)= í 01X1 ý Sa=36
ê X111 ú Sb=45
ê 111X ú
î 1XX0 þ
K1(f)=C1(f) Sa=10*3=30
Sb=40
Z(f)=C3(f) Sa=20
Sb=27
При минимизации не полностью определенной булевой функции множество
максимальных кубов определяется на объединении множества существенных вершин
и безразличных наборов в целях получения кубов наибольшей размерности .
2) Определение ядра покрытия .
Выполнение этого этапа реализуется с помощью таблицы покрытий .
Kаждая строка таблицы - максимальный куб(простая импликанта).
Каждый столбец - существенная вершина булевой функции (безразличные наборы не
включаются).
Элементы этой таблицы отражают отношение покрытия ,то есть на пересечении i-
ой строки и j-ого столбца ставится некоторая отметка в том случае если i-ый
максимальный куб покрывает j-ую вершину .
Таблицу покрытий иногда называют импликантной таблицей с учетом того ,что
каждый максимальный куб соответствует простой импликанте а существенные
вершины конституантам
единицы(нуля).
Существенные вершины
| макс. Кубы | 0000 | 0001 | 0101 | 0111 | 1000 | 1010 | 1100 | 1110 | 1111 | | A | 000X | * | * | | | | | | | | | | | | | B | X000 | * | | | | | * | | | | | | | | | C | 0X01 | | * | * | | | | | | | | | | | | D | 01X1 | | | * | * | | | | | | | | | | | E | X111 | | | | * | | | | | | | | | * | | F | 111X | | | | | | | | | | | | | * | | 1XX0 | | | | | | * | | * | | * | | * | | | | a | b | c | d | | | | | | | | | e |
Страницы: 1, 2
|
|
|
|
|

 Геометрическим местом 0-куба является точка, представляющая существенную
вершину.
Два соседних 0-куба являются концами какого-либо ребра.
Геометрическим местом 1-куба является ребро, замыкаемое склеивающимися 0-
кубами, образующими данный 1-куб.
Два параллельных ребра, образующих грань, являются образами склеивающихся 1-
кубов. В соответствии с этим геометрической интерпретацией 2-куба является
грань, образуемая парой параллельных ребер. Так как любую грань можно
определить одной из пар параллельных ребер, 2-куб может быть получен как
результат склеивания двух различных пар 1-кубов, то есть представляется в
двух экземплярах.
Геометрическим образом 3-куба можно считать 3-х мерный куб. Так как он может
быть образован 3-мя способами как пара параллельных граней, то при склеивании
он получается в трех экземплярах.
Покрытия булевых функций.
Между кубами различной размерности, входящих в кубический комплекс K(f),
существует отношение включения или покрытия. Принято говорить, что куб А
меньшей размерности покрывается кубом Б большей размерности, если куб А
включается в куб Б. Это означает, что при образовании куба Б хотя бы в одном
склеивании учавствует куб А.
Отношение включения (покрытия) между кубами принято обозначать АÌБ. В
теории множеств отношение включения связывает между собой некоторое множество
и его подмножества.
Для рассмотренного примера отношения включения имеют место между
001Ì0х1; 011Ìx11Ìx1x... любой 1-куб покрывает 2 0-куба,
2-куб - 4 0-куба и 2 1-куба, 3-куб покрывает 8 0-кубов, 12 1-кубов и 6 2-
кубов.
Покрытием булевой функции f называется такое подмножество кубов из
кубического комплекса K(f), которое покрывает все существенные вершины
функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие
конъюнктивный терм, для любого покрытия можно представить некоторую ДНФ
булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K0
(f), покрытие c0(f)=K0(f). Этому покрытию соответствует
КДНФ.
Для примера покрытием является также
|0x1
|01x
c1(f)=K1(f)=|x10
|x11
|11x
этому покрытию соответствует ДНФ вида
_ _ _ _ _ _ _ _ _ _
f=x1x3vx1x2vx2x3vx2x3vx1x2 приведенная ДНФ не является минимальной.
В качестве минимальной еще одного покрытия можно использовать множество
максимальных кубов
|0x1
c2(f)=|x1x
Действительно, куб 0х1 покрывает существенные вершины 0х1É(001, 011),
а куб x1xÉ(010, 011, 110, 111).
Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытие c2(f) соответствует ДНФ вида х1х3vx
2. Эта ДНФ является минимальной. Покрытие булевой функции, которое
соответствует минимальной ДНФ называется минимальным покрытием.
Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае все множество максимальных кубов является минимальным
покрытием. Это справедливо для нашего примера. В общем случае множество
максимальных кубов является избыточным и для получения минимального покрытия
достаточно взять некоторое его подмножество.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
|000 (1) |00x (1-2)
|001 (2) |x00 (1-3)
K0(f)=|100 (3) K1(f)=|1x0 (3-4)
|110 (4) |11x (4-5)
|111 (5)
Для данного примера множество максимальных кубов совпадает с комплексом K1
(f). Z(f)=K1(f)
Минимальными покрытиями являются
|00x |00x
с1(f)=|11x c2(f)=|11x
|x00 |1x0
Из анализа покрытия существенных вершин максимальными кубами из комплекса K
1(f) следует :
1) Куб 00х должен обязательно включаться в покрытие, так как только он
покрывает существенную вершину 001, аналогично 11х покрывает 111.
Множество максимальных кубов без которых не может быть образовано покрытие
булевой функции называется ядром покрытия T(f)=|00x
|11x
2) Так как ядром покрытия кроме существенных вершин 001 и 111 покрываются
также существенные вершины 000 и 110, то не покрытой ядром остается только
существенная вершина 100. Для ее покрытия достаточно взять 1 из оставшихся
максимальных кубов (х00 или 1х0).
Выводы :
Задача получения минимальной ДНФ сводится к задаче получения минимального
покрытия.
Получение минимального покрытия реализуется в таком порядке : а) Находится
множество максимальных кубов б) Выделяется ядро покрытия в) Из максимальных
кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое
покрывает существенные вершины, не покрытые ядром.
Цена покрытия.
Цена r-куба представляет собой количество несвязанных координат. Sr=n*r
Для оценки качества покрытия используют два вида цены покрытия :
m
1) Sa=åSrNr, где Nr - количество r-кубов, входящих в по-
r=0
крытие, m - максимальная размерность куба. Цена Sa представляет
собой сумму цен кубов, входящих в покрытие.
2) Sb=Sa+k, где k - количество кубов, входящих в покрытие
m m
Sa =å(n-r) Nr ; Sb=å(n-r)(Nr+1)
r=0 r=0
Под минимальным покрытием понимают покрытие, обладающее минимальной ценой S
a по сравнению с любым другим покрытием этой функции.
Можно показать, что покрытие, обладающее минимальной ценой Sa
обладает также и минимальной ценой Sb.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
C0(f)=K0(f) ; Sa=5*3=15 ; Sb=Sa+5=20
C1(f)=K1(f) ; Sa=4*2=8 ; Sb=Sa+4=12
Cmin(f) : Sa=3*2=6 ; Sb=9
Цена покрытия Sa представляет собой количество букв, входящих в ДНФ,
которая соответствует данному покрытию.
Цена Sb представляет для ДНФ сумму количества букв и количества термов.
Геометрическим местом 0-куба является точка, представляющая существенную
вершину.
Два соседних 0-куба являются концами какого-либо ребра.
Геометрическим местом 1-куба является ребро, замыкаемое склеивающимися 0-
кубами, образующими данный 1-куб.
Два параллельных ребра, образующих грань, являются образами склеивающихся 1-
кубов. В соответствии с этим геометрической интерпретацией 2-куба является
грань, образуемая парой параллельных ребер. Так как любую грань можно
определить одной из пар параллельных ребер, 2-куб может быть получен как
результат склеивания двух различных пар 1-кубов, то есть представляется в
двух экземплярах.
Геометрическим образом 3-куба можно считать 3-х мерный куб. Так как он может
быть образован 3-мя способами как пара параллельных граней, то при склеивании
он получается в трех экземплярах.
Покрытия булевых функций.
Между кубами различной размерности, входящих в кубический комплекс K(f),
существует отношение включения или покрытия. Принято говорить, что куб А
меньшей размерности покрывается кубом Б большей размерности, если куб А
включается в куб Б. Это означает, что при образовании куба Б хотя бы в одном
склеивании учавствует куб А.
Отношение включения (покрытия) между кубами принято обозначать АÌБ. В
теории множеств отношение включения связывает между собой некоторое множество
и его подмножества.
Для рассмотренного примера отношения включения имеют место между
001Ì0х1; 011Ìx11Ìx1x... любой 1-куб покрывает 2 0-куба,
2-куб - 4 0-куба и 2 1-куба, 3-куб покрывает 8 0-кубов, 12 1-кубов и 6 2-
кубов.
Покрытием булевой функции f называется такое подмножество кубов из
кубического комплекса K(f), которое покрывает все существенные вершины
функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие
конъюнктивный терм, для любого покрытия можно представить некоторую ДНФ
булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K0
(f), покрытие c0(f)=K0(f). Этому покрытию соответствует
КДНФ.
Для примера покрытием является также
|0x1
|01x
c1(f)=K1(f)=|x10
|x11
|11x
этому покрытию соответствует ДНФ вида
_ _ _ _ _ _ _ _ _ _
f=x1x3vx1x2vx2x3vx2x3vx1x2 приведенная ДНФ не является минимальной.
В качестве минимальной еще одного покрытия можно использовать множество
максимальных кубов
|0x1
c2(f)=|x1x
Действительно, куб 0х1 покрывает существенные вершины 0х1É(001, 011),
а куб x1xÉ(010, 011, 110, 111).
Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытие c2(f) соответствует ДНФ вида х1х3vx
2. Эта ДНФ является минимальной. Покрытие булевой функции, которое
соответствует минимальной ДНФ называется минимальным покрытием.
Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае все множество максимальных кубов является минимальным
покрытием. Это справедливо для нашего примера. В общем случае множество
максимальных кубов является избыточным и для получения минимального покрытия
достаточно взять некоторое его подмножество.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
|000 (1) |00x (1-2)
|001 (2) |x00 (1-3)
K0(f)=|100 (3) K1(f)=|1x0 (3-4)
|110 (4) |11x (4-5)
|111 (5)
Для данного примера множество максимальных кубов совпадает с комплексом K1
(f). Z(f)=K1(f)
Минимальными покрытиями являются
|00x |00x
с1(f)=|11x c2(f)=|11x
|x00 |1x0
Из анализа покрытия существенных вершин максимальными кубами из комплекса K
1(f) следует :
1) Куб 00х должен обязательно включаться в покрытие, так как только он
покрывает существенную вершину 001, аналогично 11х покрывает 111.
Множество максимальных кубов без которых не может быть образовано покрытие
булевой функции называется ядром покрытия T(f)=|00x
|11x
2) Так как ядром покрытия кроме существенных вершин 001 и 111 покрываются
также существенные вершины 000 и 110, то не покрытой ядром остается только
существенная вершина 100. Для ее покрытия достаточно взять 1 из оставшихся
максимальных кубов (х00 или 1х0).
Выводы :
Задача получения минимальной ДНФ сводится к задаче получения минимального
покрытия.
Получение минимального покрытия реализуется в таком порядке : а) Находится
множество максимальных кубов б) Выделяется ядро покрытия в) Из максимальных
кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое
покрывает существенные вершины, не покрытые ядром.
Цена покрытия.
Цена r-куба представляет собой количество несвязанных координат. Sr=n*r
Для оценки качества покрытия используют два вида цены покрытия :
m
1) Sa=åSrNr, где Nr - количество r-кубов, входящих в по-
r=0
крытие, m - максимальная размерность куба. Цена Sa представляет
собой сумму цен кубов, входящих в покрытие.
2) Sb=Sa+k, где k - количество кубов, входящих в покрытие
m m
Sa =å(n-r) Nr ; Sb=å(n-r)(Nr+1)
r=0 r=0
Под минимальным покрытием понимают покрытие, обладающее минимальной ценой S
a по сравнению с любым другим покрытием этой функции.
Можно показать, что покрытие, обладающее минимальной ценой Sa
обладает также и минимальной ценой Sb.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
C0(f)=K0(f) ; Sa=5*3=15 ; Sb=Sa+5=20
C1(f)=K1(f) ; Sa=4*2=8 ; Sb=Sa+4=12
Cmin(f) : Sa=3*2=6 ; Sb=9
Цена покрытия Sa представляет собой количество букв, входящих в ДНФ,
которая соответствует данному покрытию.
Цена Sb представляет для ДНФ сумму количества букв и количества термов.
 Цена покрытия хорошо согласуется с ценой схемы по Квайну, которая строится по
нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ=9=Sb (9-число входов).
В принципе, между SQ и ценами Sa и Sb
существует соотношение Sa £ SQ £ Sb
Это неравенство имеет место при следующих допущениях по комбинационной схеме :
1) Схема строится по нормальной форме (ДНФ или КНФ).
2) Схема строится на элементах булевого базиса (И, ИЛИ).
3) На входы схемы можно подавать как прямые, так и инверсные значения входных
переменных, представляющие собой значения аргументов булевой функции (схема с
парафазными входами). Элементы НЕ (инвертора в схеме отсутствуют.
Нулевое покрытие булевой функции и получение минимальной КНФ.
Выше было рассмотрено покрытие булевой функции на наборах аргументов для
которых функция равна единице.
Такие покрытия можно назвать единичными. Наряду с единичными покрытиями
существуют и нулевые, для которых покрываются наборы аргументов, на которых
функция равна нулю, то есть покрытие реализуется для существенных вершин, но
не самой функции, а ее отрицания (инверсии).
Нулевое покрытие строится также как и единичное, но только для отрицания
исходной функции.
f3(x)=V(0,1,4,6,7) f3(x)=&(2,3,5)
(f=1) (f=0) _ |010
K0( f )=|011
_ _ |101
C0( f )= K0( f ) Sa=9 Sb=12
_ _ _
K1( f )=|01x Z( f )=Cmin( f )=|01x Sa=5 Sb=7
|101
Цена минимального нулевого покрытия оказалась меньше цены минимального
единичного покрытия.
Так как заранее предсказать невозможно, какое из минимальных покрытий данной
функции, единичное или нулевое, будет иметь меньшую цену, то для построения
схемы, обладающей минимальной ценой по Квайну, целесообразно решать задачу
минимзации в отношении обоих покрытий.
Импликанты булевой функции.
Системы импликант.
Решение задачи минимизации булевой функции методом Квайна и
усовершенствованным методом Квайна-МакКласски базируется на понятиях
импликант и их систем.
Определение : Булева функция g(x) называется импликантой булевой функции
f(x), если для любого набора аргументов, на которых g(x)=1, f(x) также равна
единице.
~ ~ ~
g( x )=1 => f( x )=1, где х - некоторый набор аргументов.
Свойства импликант :
1) Между импликантой и самой функцией существует отношение включения
g(x)Ìf(x).
2) Можно утверждать, что для любого набора аргументов, на котором функция
равна нулю, ее импликанта также равна нулю.
3) Если g(x) и j(x) являются импликантами функции f(x), то их дизъюнкция
также является импликантой этой функции.
Простейшими примерами импликант могут служить конъюнктивные термы, входящие в
ДНФ данной функции.
Пример : для f3(x)=V(0,1,4,6,7) (#)
(f=1) _ _ _
импликантами являются х1х2х3; х1х2х3; х1х2;...
Произвольная дизъюнкция этих термов также является импликантой функции.
Определение : Простой (первичной) импликантой булевой функции называется
конъюнктивный терм, который сам является импликантой этой функции, но никакая
его собственная часть уже не является импликантой этой функции.
Под собственной частью терма понимается новый терм, полученный из исходного,
путем вычеркивания произвольного числа букв.
Для данного примера функции (#) простыми импликантами являются :
_ _ _
х1х2х3; х1х2х3; х1х2;...
Множеству простых импликант можно поставить в соответствие множество
максимальных кубов.
Определение : Дизъюнкция всех простых импликант булевой функции представляет
собой ДНФ этой функции, которая называется сокращенной - СДНФ.
Для функции (#) из приведенного примера
_ _ _ _ _
СДНФ : y= х1х2v х1х2vх2х3v х1х3
Понятие «сокращенное» присвоено ДНФ в том смысле, что она, как правило,
содержит меньшее количество букв и термов по сравнению с КДНФ. Для нашего
примера КДНФ содержит 15 букв и 5 термов, а СДНФ - 8 букв и 4 терма.
Аналогия между импликантами и кубическим представлением Булевой функции
Любому кубу из К(f) можно поставить в соответствие конъюнктивный терм который
можно рассматривать как импликанту булевой функции .Любой простой импликанте
булевой функции соответствует максимальный куб ,и в свою очередь множество
всех простых импликант соответствует множеству Z(f) всех максимальных кубов
К(f).
Таким образом можно провести некоторую аналогию между сокращенной СДНФ и Z(f).
В отношении импликант булевой функции также как и в отношении кубов
соответствующих им существует отношение покрытия.
Принято считать ,что импликанта покрывает некоторую существенную вершину или
в общем случае некоторый куб из К(f) ,если значение импликанты на наборе
аргументов представляющем данную существенную вершину равно 1 или в общем
случае значение импликанты равно 1 для всех существенных вершин покрываемых
кубом из К(f).
ПРИМЕР : импликанта х1х2 покрывает существенные вершины
(110,111) и в свою очередь покрывает куб 11х.
Определение :множество импликант булевой функции образует полную систему
импликант ,если любая существенная вершина булевой функции покрывается хотя
бы одной импликантой этого множества.
Если считать ,что в полную систему импликант включаются импликанты только в
виде конъюнктивных термов и не включает импликанты в виде дизъюнктивных
термов ,то полной системе импликант можно поставить в соответствие некоторое
множество кубов из К(f) образующих покрытие булевой функции f .
Так например ,кубам из кубического комплекса К°(f) соответствует полная
система импликант ,представляющая собой множество конституент 1 данной
функции f. В свою очередь множеству максимальных кубов Z(f) ,естественно
образующих покрытие булевой функции ,соответствует полная система простых
импликант.
Определение :система простых импликант называется приведенной ,если она
является полной ,а никакая ее собственная часть уже не образует полную
систему импликант.
Для функции y= x 1 x 2 Ú
Цена покрытия хорошо согласуется с ценой схемы по Квайну, которая строится по
нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ=9=Sb (9-число входов).
В принципе, между SQ и ценами Sa и Sb
существует соотношение Sa £ SQ £ Sb
Это неравенство имеет место при следующих допущениях по комбинационной схеме :
1) Схема строится по нормальной форме (ДНФ или КНФ).
2) Схема строится на элементах булевого базиса (И, ИЛИ).
3) На входы схемы можно подавать как прямые, так и инверсные значения входных
переменных, представляющие собой значения аргументов булевой функции (схема с
парафазными входами). Элементы НЕ (инвертора в схеме отсутствуют.
Нулевое покрытие булевой функции и получение минимальной КНФ.
Выше было рассмотрено покрытие булевой функции на наборах аргументов для
которых функция равна единице.
Такие покрытия можно назвать единичными. Наряду с единичными покрытиями
существуют и нулевые, для которых покрываются наборы аргументов, на которых
функция равна нулю, то есть покрытие реализуется для существенных вершин, но
не самой функции, а ее отрицания (инверсии).
Нулевое покрытие строится также как и единичное, но только для отрицания
исходной функции.
f3(x)=V(0,1,4,6,7) f3(x)=&(2,3,5)
(f=1) (f=0) _ |010
K0( f )=|011
_ _ |101
C0( f )= K0( f ) Sa=9 Sb=12
_ _ _
K1( f )=|01x Z( f )=Cmin( f )=|01x Sa=5 Sb=7
|101
Цена минимального нулевого покрытия оказалась меньше цены минимального
единичного покрытия.
Так как заранее предсказать невозможно, какое из минимальных покрытий данной
функции, единичное или нулевое, будет иметь меньшую цену, то для построения
схемы, обладающей минимальной ценой по Квайну, целесообразно решать задачу
минимзации в отношении обоих покрытий.
Импликанты булевой функции.
Системы импликант.
Решение задачи минимизации булевой функции методом Квайна и
усовершенствованным методом Квайна-МакКласски базируется на понятиях
импликант и их систем.
Определение : Булева функция g(x) называется импликантой булевой функции
f(x), если для любого набора аргументов, на которых g(x)=1, f(x) также равна
единице.
~ ~ ~
g( x )=1 => f( x )=1, где х - некоторый набор аргументов.
Свойства импликант :
1) Между импликантой и самой функцией существует отношение включения
g(x)Ìf(x).
2) Можно утверждать, что для любого набора аргументов, на котором функция
равна нулю, ее импликанта также равна нулю.
3) Если g(x) и j(x) являются импликантами функции f(x), то их дизъюнкция
также является импликантой этой функции.
Простейшими примерами импликант могут служить конъюнктивные термы, входящие в
ДНФ данной функции.
Пример : для f3(x)=V(0,1,4,6,7) (#)
(f=1) _ _ _
импликантами являются х1х2х3; х1х2х3; х1х2;...
Произвольная дизъюнкция этих термов также является импликантой функции.
Определение : Простой (первичной) импликантой булевой функции называется
конъюнктивный терм, который сам является импликантой этой функции, но никакая
его собственная часть уже не является импликантой этой функции.
Под собственной частью терма понимается новый терм, полученный из исходного,
путем вычеркивания произвольного числа букв.
Для данного примера функции (#) простыми импликантами являются :
_ _ _
х1х2х3; х1х2х3; х1х2;...
Множеству простых импликант можно поставить в соответствие множество
максимальных кубов.
Определение : Дизъюнкция всех простых импликант булевой функции представляет
собой ДНФ этой функции, которая называется сокращенной - СДНФ.
Для функции (#) из приведенного примера
_ _ _ _ _
СДНФ : y= х1х2v х1х2vх2х3v х1х3
Понятие «сокращенное» присвоено ДНФ в том смысле, что она, как правило,
содержит меньшее количество букв и термов по сравнению с КДНФ. Для нашего
примера КДНФ содержит 15 букв и 5 термов, а СДНФ - 8 букв и 4 терма.
Аналогия между импликантами и кубическим представлением Булевой функции
Любому кубу из К(f) можно поставить в соответствие конъюнктивный терм который
можно рассматривать как импликанту булевой функции .Любой простой импликанте
булевой функции соответствует максимальный куб ,и в свою очередь множество
всех простых импликант соответствует множеству Z(f) всех максимальных кубов
К(f).
Таким образом можно провести некоторую аналогию между сокращенной СДНФ и Z(f).
В отношении импликант булевой функции также как и в отношении кубов
соответствующих им существует отношение покрытия.
Принято считать ,что импликанта покрывает некоторую существенную вершину или
в общем случае некоторый куб из К(f) ,если значение импликанты на наборе
аргументов представляющем данную существенную вершину равно 1 или в общем
случае значение импликанты равно 1 для всех существенных вершин покрываемых
кубом из К(f).
ПРИМЕР : импликанта х1х2 покрывает существенные вершины
(110,111) и в свою очередь покрывает куб 11х.
Определение :множество импликант булевой функции образует полную систему
импликант ,если любая существенная вершина булевой функции покрывается хотя
бы одной импликантой этого множества.
Если считать ,что в полную систему импликант включаются импликанты только в
виде конъюнктивных термов и не включает импликанты в виде дизъюнктивных
термов ,то полной системе импликант можно поставить в соответствие некоторое
множество кубов из К(f) образующих покрытие булевой функции f .
Так например ,кубам из кубического комплекса К°(f) соответствует полная
система импликант ,представляющая собой множество конституент 1 данной
функции f. В свою очередь множеству максимальных кубов Z(f) ,естественно
образующих покрытие булевой функции ,соответствует полная система простых
импликант.
Определение :система простых импликант называется приведенной ,если она
является полной ,а никакая ее собственная часть уже не образует полную
систему импликант.
Для функции y= x 1 x 2 Ú