|
|
|
|
Лекция: Курс лекций по теории вероятностей
Во втором случае пусть k0 = [np + p] (целая часть
числа np + p, то есть наибольшее целое число, не превосходящее np +
p). Из неравенств (a), (b) следует, что
Действительно, неравенство Р(vn = k0) > Р(vn
= k0+1), например, следует из (b), примененного для
k = k0+1 > np + p.
Видим, что в зависимости от того, является число 1 > np + p целым или
нет, имеется либо два равновероятных «наиболее вероятных» числа успехов k
0 = np + p и k0 –1 > np + p - 1,либо одно
«наиболее вероятное» число успехов k0 = [np + p].
Сформулируем уже доказанное утверждение в виде теоремы.
Теорема 12. В n испытаниях схемы Бернулли с вероятностью успеха
p наиболее вероятным числом успехов является
a) единственное число k0 = [np + p], если число np + p не целое;
б) два числа k0 = np + p и k0 -1= np + p -1, если число np + p целое.
Пример 19. Если p = q = 1/2, то при четном числе испытаний n
число np + p = n/2 + 1 /2— не целое, так что наиболее вероятным является
единственное число успехов [n/2 + 1 /2] = n/2. Что совершенно
понятно, так как есть нечетное число возможностей — получить 0, 1, .n
успехов, причем вероятности получить k и n-k успехов одинаковы.
При нечетном же числе испытаний n число np + p = n/2 + 1 /2 —
целое, так что наиболее вероятными (и одинаково вероятными) являются два числа
успехов n/2 + 1 /2 и n/2 - 1 /2.
5.3 Номер первого успешного испытания
Рассмотрим схему Бернулли с вероятностью успеха p в одном испытании.
Испытания проводятся до появления первого успеха. Введем величину τ
, равную номеру первого успешного испытания.
Теорема 13. Вероятность того, что первый успех произойдет в испытании с
номером k, равна
P(τ = k) = p qk-1.
Доказательство. Действительно,
Определение 21. Набор чисел {p qk-1 }
называется геометрическим распределением вероятностей и обозначается G
p или G(p).
Геометрическое распределение вероятностей обладает интересным свойством, которое
можно назвать свойством «нестарения». Пусть величина τ обозначает, скажем,
время безотказной работы (измеряемое целым числом часов) некоторого устройства.
Предположим, что для величины τ вероятность принять любое свое значение k
в точности равна pqk-1. Справедливо следующее
утверждение.
Теорема 14. Пусть P(τ = k) = p qk-1. Тогда для произвольных n, k ³ 0
P(τ > n+k\ τ > n) = P(τ > k)
Данному равенству можно придать следующее звучание: если известно, что
устройство проработало без отказов n часов, то вероятность ему работать еще не
менее k часов точно такая же, как вероятность проработать не менее k часов для
нового устройства.
Можно прочесть эту формулу и так: вероятность работающему устройству
проработать еще сколько-то часов не зависит от того момента, когда мы начали
отсчет времени, или от того, сколько уже работает устройство.
Доказательство. По определению условной вероятности,
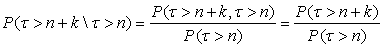 (4)
Последнее равенство следует из того, что событие {τ > n+k}
влечет событие {τ > n}, так что пересечение этих событий есть
{τ > n+k}. Найдем для произвольного m ³ 0 вероятность
P(τ > m).
Можно также заметить, что событие {τ > m} означает, что в схеме
Бернулли первые m испытаний завершились «неудачами», а это событие имеет
вероятность как раз qm.
Возвращаясь к (4), получим
5.4 Приближение гипергеометрического распределения биномиальным
Рассмотрим урну, содержащую N шаров, из которых K шаров — белые,
а оставшиеся N-K шаров — черные. Из урны наудачу (без возвращения)
выбираются n шаров. Вероятность PN,K
(n, k) того, что будет выбрано ровно k белых и n-k черных
шаров, находится по формуле (см. определение 8 гипергеометрического
распределения вероятностей):
Если число шаров в урне очень велико, то извлечение одного, двух, трех шаров
почти не меняет пропорцию белых и черных шаров в урне, так что вероятности P
N,K(n, k) не очень отличаются от вероятностей в
процедуре выбора с возвращением
P(получить ровно k белых шаров при выборе n шаров с возвращением) =
Сформулируем нашу первую предельную теорему.
Теорема 15. Если N → ∞ и K → ∞
так, что K/N → p Î (0, 1) то для любых фиксированных n,
0<=k<=n (4)
Последнее равенство следует из того, что событие {τ > n+k}
влечет событие {τ > n}, так что пересечение этих событий есть
{τ > n+k}. Найдем для произвольного m ³ 0 вероятность
P(τ > m).
Можно также заметить, что событие {τ > m} означает, что в схеме
Бернулли первые m испытаний завершились «неудачами», а это событие имеет
вероятность как раз qm.
Возвращаясь к (4), получим
5.4 Приближение гипергеометрического распределения биномиальным
Рассмотрим урну, содержащую N шаров, из которых K шаров — белые,
а оставшиеся N-K шаров — черные. Из урны наудачу (без возвращения)
выбираются n шаров. Вероятность PN,K
(n, k) того, что будет выбрано ровно k белых и n-k черных
шаров, находится по формуле (см. определение 8 гипергеометрического
распределения вероятностей):
Если число шаров в урне очень велико, то извлечение одного, двух, трех шаров
почти не меняет пропорцию белых и черных шаров в урне, так что вероятности P
N,K(n, k) не очень отличаются от вероятностей в
процедуре выбора с возвращением
P(получить ровно k белых шаров при выборе n шаров с возвращением) =
Сформулируем нашу первую предельную теорему.
Теорема 15. Если N → ∞ и K → ∞
так, что K/N → p Î (0, 1) то для любых фиксированных n,
0<=k<=n
5.5 Независимые испытания с несколькими исходами
Рассмотрим следующий пример, когда из двух очень похожих вопросов на один
можно ответить, пользуясь формулой Бернулли, а для другого этой формулы
оказывается недостаточно:
Пример 20. Игральная кость подбрасывается 15 раз. Найти вероятности
следующих событий:
а) выпадет ровно 10 шестерок; б) выпадет ровно 10 шестерок и три единицы.
а) есть 15 испытаний схемы Бернулли с вероятностью успеха 1/6 (выпадение
шестерки). Вероятность десяти успехов в 15 испытаниях равна
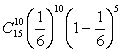 б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки,
выпадение единицы, выпадение остальных граней. Воспользоваться формулой для
числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.
Осталось изобрести формулу для подсчета вероятности каждому исходу в
нескольких независимых испытаниях выпасть нужное число раз, если в одном
испытании возможно не два, а более исходов.
Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, .m.
Пусть исход i в одном испытании случается с вероятностью рi, 1
≤ i ≤ m и
б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки,
выпадение единицы, выпадение остальных граней. Воспользоваться формулой для
числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.
Осталось изобрести формулу для подсчета вероятности каждому исходу в
нескольких независимых испытаниях выпасть нужное число раз, если в одном
испытании возможно не два, а более исходов.
Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, .m.
Пусть исход i в одном испытании случается с вероятностью рi, 1
≤ i ≤ m и
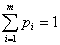 Обозначим через Р(n1,n2,.,nm) вероятность
того, что в n = n1+ n2+ .+nm независимых
испытаний исход 1 появился n1, раз, исход 2 – n2 раз,.
Теорема 16. Для любого n и любых целых n1
≥ 0. nm ≥ 0 таких, что n
1+ n2+ .+nm = n, верна формула:
Обозначим через Р(n1,n2,.,nm) вероятность
того, что в n = n1+ n2+ .+nm независимых
испытаний исход 1 появился n1, раз, исход 2 – n2 раз,.
Теорема 16. Для любого n и любых целых n1
≥ 0. nm ≥ 0 таких, что n
1+ n2+ .+nm = n, верна формула:
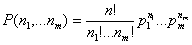 Доказательство. Рассмотрим один элементарный исход, благоприятствующий
выпадению n1 единиц, n2 двоек, . , n
m раз m-ок:
Доказательство. Рассмотрим один элементарный исход, благоприятствующий
выпадению n1 единиц, n2 двоек, . , n
m раз m-ок:
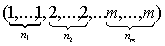 Это результат n экспериментов, когда все нужные исходы появились в
некотором заранее заданном порядке. Вероятность такого результата n
независимых испытаний равна
Это результат n экспериментов, когда все нужные исходы появились в
некотором заранее заданном порядке. Вероятность такого результата n
независимых испытаний равна
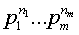 Все остальные благоприятные исходы отличаются лишь расположением чисел 1, 2,
.m на n местах. Число таких исходов равно числу способов расставить
на n местах n1 единиц, n2 двоек,
, . , nm раз чисел m, то есть
Все остальные благоприятные исходы отличаются лишь расположением чисел 1, 2,
.m на n местах. Число таких исходов равно числу способов расставить
на n местах n1 единиц, n2 двоек,
, . , nm раз чисел m, то есть
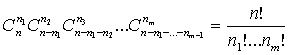 Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как
вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего
исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10
шестерок, 3 единицы и еще 2 других очка равна
Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как
вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего
исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10
шестерок, 3 единицы и еще 2 других очка равна
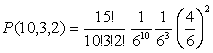
5.6 Теорема Пуассона для схемы Бернулли
Предположим, нам нужна вероятность получить не менее десяти успехов в 1000
испытаний схемы Бернулли с вероятностью успеха 0.003. Вероятность этого
события равна любому из следующих выражений:
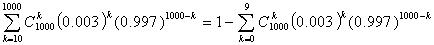 и вычисление даже одного слагаемого в каждом из этих выражений весьма
проблематично.
Сформулируем теорему о приближенном вычислении вероятности какого-либо числа
успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью
успеха. Термин «большое число» должен означать n → ∞. Если
при этом p = pn→ 0,то, очевидно, вероятность получить
любое конечное число успехов при растущем числе испытаний стремится к нулю.
Необходимо чтобы вероятность успеха p = pn→ 0
одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность
успеха меняться не может (см. определение схемы Бернулли).
Поэтому рассмотрим «схему серий»: есть
одно испытание ○ с вероятностью успеха p1
два испытания ○ , ○ с вероятностью успеха p2
.
n испытаний ○ , . , ○ с вероятностью успеха pn
.
Вероятность успеха меняется не внутри одной серии испытаний, а от серии к
серии, когда меняется общее число испытаний. Обозначим через vn
число успехов в n-той серии испытаний.
Теорема 17 (Теорема Пуассона).
Пусть n → ∞ , pn→ 0 так, что n
pn→ λ > 0. Тогда для любого k ≥
0 вероятность получить k успехов в n испытаниях схемы Бернулли с
вероятностью успеха pn стремится к величине
и вычисление даже одного слагаемого в каждом из этих выражений весьма
проблематично.
Сформулируем теорему о приближенном вычислении вероятности какого-либо числа
успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью
успеха. Термин «большое число» должен означать n → ∞. Если
при этом p = pn→ 0,то, очевидно, вероятность получить
любое конечное число успехов при растущем числе испытаний стремится к нулю.
Необходимо чтобы вероятность успеха p = pn→ 0
одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность
успеха меняться не может (см. определение схемы Бернулли).
Поэтому рассмотрим «схему серий»: есть
одно испытание ○ с вероятностью успеха p1
два испытания ○ , ○ с вероятностью успеха p2
.
n испытаний ○ , . , ○ с вероятностью успеха pn
.
Вероятность успеха меняется не внутри одной серии испытаний, а от серии к
серии, когда меняется общее число испытаний. Обозначим через vn
число успехов в n-той серии испытаний.
Теорема 17 (Теорема Пуассона).
Пусть n → ∞ , pn→ 0 так, что n
pn→ λ > 0. Тогда для любого k ≥
0 вероятность получить k успехов в n испытаниях схемы Бернулли с
вероятностью успеха pn стремится к величине
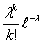 (5)
(5)
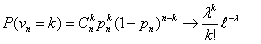 для n → ∞ , pn→ 0 так, что n pn→ λ
Определение 22. Пусть λ > 0— некоторая постоянная. Набор
чисел для n → ∞ , pn→ 0 так, что n pn→ λ
Определение 22. Пусть λ > 0— некоторая постоянная. Набор
чисел 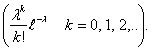 называется
распределением Пуассона с параметром λ.
Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее
десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с
вычисления которой мы начали. Поскольку n = 1000 «велико», а p
n = 0.003 «мало», то, взяв λ = n pn = 3 ,
можно написать приближенное равенство называется
распределением Пуассона с параметром λ.
Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее
десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с
вычисления которой мы начали. Поскольку n = 1000 «велико», а p
n = 0.003 «мало», то, взяв λ = n pn = 3 ,
можно написать приближенное равенство
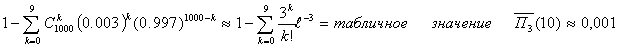 (6)
Осталось решить, а достаточно ли n=103 «велико», а p
n = 0.003 «мало», чтобы заменить точную вероятность P(vn
= k) на приближенное значение
(6)
Осталось решить, а достаточно ли n=103 «велико», а p
n = 0.003 «мало», чтобы заменить точную вероятность P(vn
= k) на приближенное значение
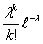 Для этого нужно уметь оценивать разницу между этими двумя вероятностями.
Теорема 18 (Теорема Пуассона с оценкой погрешности).
Пусть A Í {0, 1, ., n} — произвольное множество целых
неотрицательных чисел, vn — число успехов в n
испытаниях схемы Бернулли с вероятностью успеха p, λ = n p.
Тогда
Для этого нужно уметь оценивать разницу между этими двумя вероятностями.
Теорема 18 (Теорема Пуассона с оценкой погрешности).
Пусть A Í {0, 1, ., n} — произвольное множество целых
неотрицательных чисел, vn — число успехов в n
испытаниях схемы Бернулли с вероятностью успеха p, λ = n p.
Тогда
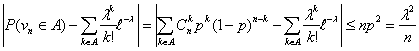 Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно
ли n «велико», а p «мало», руководствуясь полученной величиной
погрешности.
Какова же погрешность в формуле (6)?
Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно
ли n «велико», а p «мало», руководствуясь полученной величиной
погрешности.
Какова же погрешность в формуле (6)?
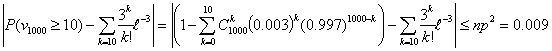 Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае,
можно утверждать, что искомая вероятность никак не больше, чем
0,01=0,001+0,009.
Рассмотрим еще одну формулу приближенного вычисления pn (m)
когда n велико. В отличии от предыдущего результата число успехов m в
этом случае тоже растет с ростом n, а вероятность успеха постоянна.
Локальная теорема Муавра – Лапласа
Пусть
Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае,
можно утверждать, что искомая вероятность никак не больше, чем
0,01=0,001+0,009.
Рассмотрим еще одну формулу приближенного вычисления pn (m)
когда n велико. В отличии от предыдущего результата число успехов m в
этом случае тоже растет с ростом n, а вероятность успеха постоянна.
Локальная теорема Муавра – Лапласа
Пусть 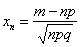 .Предположим, что .Предположим, что 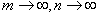 и величины и величины 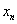 являются ограниченными. Тогда являются ограниченными. Тогда
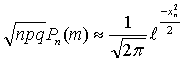 В частности, если
В частности, если 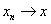 , то , то
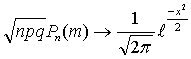 Доказательство:
В силу ограниченности величин
Доказательство:
В силу ограниченности величин 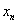 разность
разность 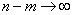 вместе с
n и m Воспользуемся формулой Стирлинга вместе с
n и m Воспользуемся формулой Стирлинга
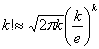
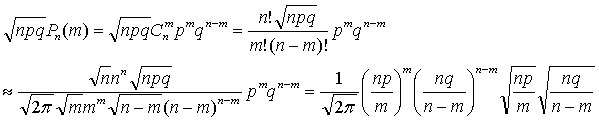 В силу определения
В силу определения 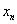
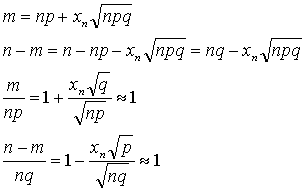
Раздел 6. Случайные величины и их распределения 6.1 Случайные величины
Мы уже видели, что для очень многих экспериментов нет никаких различий в
подсчете вероятностей событий, тогда как элементарные исходы в этих
экспериментах очень различаются. Но нас и должны интересовать именно
вероятности событий, а не структура пространства элементарных исходов. Поэтому
пора во всех таких «похожих» экспериментах вместо самых разных элементарных
исходов использовать, например, числа. То есть ввести соответствие (иначе
говоря, отображение) между элементарными исходами и вещественными числами (с
ними удобно работать).
Пусть имеется случайный эксперимент и задано вероятностное пространство
(Ω, Ψ,Р).
Определение 23. Функция ξ: Ω →R называется
случайной величиной, если для любого х Î R множество
{ ξ < x} = {ω: ξ(ω) < x} является событием, то
есть принадлежит σ-алгебре событий Ψ.
Замечание 10. Можно смело считать, что любое множество элементарных
исходов есть событие, и, следовательно, случайная величина есть
произвольная функция из Ω в R. Никаких неприятностей на
практике это обычно не влечет.
Определение 24. Будем говорить, что функция ξ: Ω →R
является Ψ -измеримой, если {ω: ξ(ω) < x}
принадлежит Ψ для любого х Î R.
Итак, случайная величина есть Ψ - измеримая функция, ставящая в
соответствие каждому элементарному исходу ω Î Ω число
ξ(ω) Î R.
Пример 21. Подбрасываем 1 раз кубик. Пусть Ω = {1, 2, 3, 4, 5,
6} , и две функции из Ω в заданы так: ξ(ω)=
ω , η(ω)= ω2.
Если Ψ есть множество всех подмножеств Ω, то
ξ и η являются случайными величинами, поскольку любое
множество элементарных исходов принадлежит Ψ, в том числе и {ω:
ξ(ω) < x} или {ω: η (ω) < x} .
Можно записать соответствие между значениями случайных величин ξ и
η вероятностями принимать эти значения в виде «таблицы распределения
вероятностей» или, коротко, «таблицы распределения»:
ξ | 1 | 2 | 3 | 4 | 5 | 6 | Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
η | 1 | 4 | 9 | 16 | 25 | 36 | Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Здесь 1/6 = Р(ξ=1)=.= Р(ξ=6) = Р(η =1)= .= Р(η =36)
Пусть σ -алгебра событий Ψ состоит всего из четырех множеств:
Ψ = { Ω ,Æ, {1,3,5},{2,4,6} }
то есть событием является, кроме достоверного и невозможного событий, выпадение
четного (соответственно, нечетного) числа очков. Убедимся, что при такой
«бедной» σ -алгебре ни ξ, ни η не
являются случайными величинами, так как эти функции не Ψ - измеримы.
Возьмем (например) x = 3,967. Видим, что
{ω Î Ω: ξ(ω) < 3,967}= {1, 2, 3}Ï
Ψ и {ω Î Ω: η (ω) < 3,967}= {1}Ï
Ψ
Теперь попробуем понять, зачем нужна Ψ - измеримость и почему требуется,
чтобы {ω: ξ(ω) < x} являлось событием.
Если задана случайная величина ξ, нам может потребоваться вычислить
вероятности типа
P(ξ = 5) = P{ω: ξ(ω) = 5},
P (ξ Î [-3,7]),
P(ξ ³ 3,2),
P(ξ > 0)
(и вообще самые разные вероятности попадания в различные множества на прямой).
Это возможно только если множества, стоящие под знаком вероятности, являются
событиями (напомню, что вероятность есть функция из σ - алгебры
событий в [0,1]).
Но если потребовать, чтобы Ax = {ω: ξ(ω) < x}
было событием при любом x, то мы из свойств σ - алгебры
сразу получим, что
и 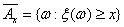 — событие, и — событие, и 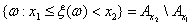 — событие,
и — событие,
и 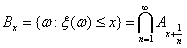 — событие,
и {ω: ξ(ω) = x}= Bx \ Ax —
событие,
(7)
и т.д., и т.п. (операции пересечения, объединения, дополнения событий не
выводят из класса событий).
Можно потребовать в определении 23 чего-нибудь другого. Например, чтобы событием
было попадание в любой интервал: (ω: ξ(ω) Î [a, b])
для любых a < b.
Или чтобы {ω: ξ(ω) ³ x} было событием для любого
x. Любое такое определение эквивалентно исходному.
Опишем различные типы распределений случайных величин. Под распределением
случайной величины мы будем понимать соответствие
«значение случайной величины ↔ вероятность принимать это значение»,
либо (чаще)
«множество на прямой ↔ вероятность случайной величине попасть в это
множество». — событие,
и {ω: ξ(ω) = x}= Bx \ Ax —
событие,
(7)
и т.д., и т.п. (операции пересечения, объединения, дополнения событий не
выводят из класса событий).
Можно потребовать в определении 23 чего-нибудь другого. Например, чтобы событием
было попадание в любой интервал: (ω: ξ(ω) Î [a, b])
для любых a < b.
Или чтобы {ω: ξ(ω) ³ x} было событием для любого
x. Любое такое определение эквивалентно исходному.
Опишем различные типы распределений случайных величин. Под распределением
случайной величины мы будем понимать соответствие
«значение случайной величины ↔ вероятность принимать это значение»,
либо (чаще)
«множество на прямой ↔ вероятность случайной величине попасть в это
множество».
6.2 Дискретные распределения
Определение 25. Говорят, что случайная величина ξ имеет
дискретное распределение, если существует конечный или счетный набор чисел
{a1, a2, .} такой, что:
а) pi = P{ ξ = ai} > 0 для всех i;
б)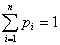 .
То есть случайная величина ξ имеет дискретное распределение, если
она принимает не более чем счетное число значений.
Определение 26. Если случайная величина ξ имеет дискретное
распределение, назовем таблицей распределения соответствие ai
↔ pi, которое чаще всего рисуют так: .
То есть случайная величина ξ имеет дискретное распределение, если
она принимает не более чем счетное число значений.
Определение 26. Если случайная величина ξ имеет дискретное
распределение, назовем таблицей распределения соответствие ai
↔ pi, которое чаще всего рисуют так:
6.3 Примеры дискретных распределений Вырожденное распределение.
Говорят, что случайная величина ξ имеет вырожденное распределение с
параметром а, и пишут ξ Î Ia
если ξ принимает единственное значение а с вероятностью 1,
то есть P(ξ = a) = 1. Таблица распределения ξ имеет
вид
Распределение Бернулли.
Говорят, что случайная величина ξ имеет распределение Бернулли с
параметром р, и пишут ξ Î Вр
, если ξ принимает значения 1 и 0 с вероятностями р и 1
- р, соответственно. Случайная величина ξ с таким
распределением равна числу успехов в одном испытании схемы Бернулли с
вероятностью успеха (0 успехов или 1 успех). Таблица распределения
ξ имеет вид
Биномиальное распределение.
Говорят, что случайная величина ξ имеет биномиальное распределение
с параметрами n и p, где 0 £ p £, n и пишут
ξ Î Вn,р
, если ξ принимает значения 0, 1, .,n с вероятностями
P(ξ = k) = Cnk pk (1-p)n
-k . Случайная величина ξ с таким
распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с
вероятностью успеха р .
Таблица распределения ξ имеет вид
ξ | 0 | 1 | . | k | . | n | Р | (1-p)n | n p(1-p)n-1 | . | Cnk pk (1-p)n-k | . | Pn |
Геометрическое распределение.
Говорят, что случайная величина τ имеет геометрическое
распределение с параметром р, где 0 £ p £, n, и
пишут τ Î Gр, если τ
принимает значения 1, 2, 3, .с вероятностями P(τ = k) =
p (1-p)k-1. Случайная величина τ с таким
распределением имеет смысл номера первого успешного испытания в схеме
Бернулли с вероятностью успеха р .
Таблица распределения τ имеет вид
τ | 1 | 2 | . | k | . | Р | p | Р (1 – р) | . | p (1-p)k-1 | . |
Распределение Пуассона.
Говорят, что случайная величина ξ имеет распределение Пуассона с
параметром λ, где λ > 0 , и ξ Î
П λ, если ξ принимает значения 0, 1,
2 . с вероятностями
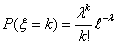 Таблица распределения ξ имеет вид
Таблица распределения ξ имеет вид
ξ | 1 | 2 | . | k | . | Р | е- λ | λ е- λ | . | (λk /k!)е- λ | . |
Гипергеометрическое распределение.
Говорят, что случайная величина ξ имеет гипергеометрическое
распределение с параметрами n, N и K, K £ N
, n £ N если ξ принимает целые значения от
max (0, N - K – n ) до min (K ,n ) с вероятностями
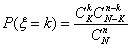 . Случайная величина ξ с таким распределением имеет смысл числа
белых шаров среди n шаров выбранных наудачу и без возвращения из урны,
содержащей К белых шаров и N-K не белых.
Заметьте, что со всеми этими распределениями мы уже хорошо знакомы.
Но распределения случайных величин далеко не исчерпываются дискретными
распределениями. Так, например, если точка бросается наудачу на отрезок
[0,1], то можно задать случайную величину, равную координате этой точки. Но
число значений этой случайной величины несчетно, так что ее распределение
дискретным не является. Да и вероятность этой случайной величине принять
каждое из своих возможных значений (попасть в точку) равна нулю. Так что не
только таблица распределения не существует, но и соответствие «значение
величины « вероятность его принять» ничего не говорит о распределении
случайной величины.
Какими же характеристиками еще можно описать распределение?
. Случайная величина ξ с таким распределением имеет смысл числа
белых шаров среди n шаров выбранных наудачу и без возвращения из урны,
содержащей К белых шаров и N-K не белых.
Заметьте, что со всеми этими распределениями мы уже хорошо знакомы.
Но распределения случайных величин далеко не исчерпываются дискретными
распределениями. Так, например, если точка бросается наудачу на отрезок
[0,1], то можно задать случайную величину, равную координате этой точки. Но
число значений этой случайной величины несчетно, так что ее распределение
дискретным не является. Да и вероятность этой случайной величине принять
каждое из своих возможных значений (попасть в точку) равна нулю. Так что не
только таблица распределения не существует, но и соответствие «значение
величины « вероятность его принять» ничего не говорит о распределении
случайной величины.
Какими же характеристиками еще можно описать распределение?
Раздел 7. Функция распределения
Заметим, что на том же отрезке [0, 1] вероятности попадания в множества
положительной меры совсем не нулевые. И термин «наудачу» мы когда-то описывали
как раз в терминах вероятностей попадания в множество. Может быть, разумно
описать распределение случайной величины, задав для любого множества,
вероятность принять значения из этого множества? Это действительно полное
описание распределения, но уж очень трудно с ней работать — слишком много
множеств на прямой.
Нельзя ли обойтись заданием вероятностей попадания в какой-нибудь меньший набор
множеств на прямой? Оказывается, что можно ограничиться только вероятностями
попадания в интервалы (-¥, х) для всех х Î R,
с помощью которых можно будет определить и вероятность попасть в любое другое
множество.
Замечание 11. Можно с таким же успехом ограничиться набором вероятностей
попадания в интервалы (-¥, х], или в (х ,¥), или в
[х ,¥), или в (х1 ,x2). Впрочем, последних
уже слишком много.
Определение 27.Функцией распределения случайной величины
ξ называется функция Fξ(x) : R ® [0,
1], при каждом x Î R равная Fξ(x)
= P(ξ < x) = P{ω: ξ(ω) < x}
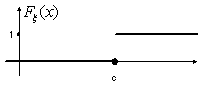
Пример 22. Случайная величина ξ имеет вырожденное распределение Ic. Тогда
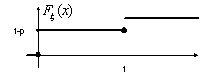
 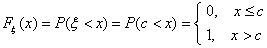 Пример 23. Случайная величина ξ имеет распределение Бернулли Вр. Тогда
Пример 23. Случайная величина ξ имеет распределение Бернулли Вр. Тогда
 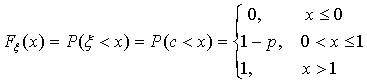 Пример 24. Будем говорить, что случайная величина ξ имеет
равномерное распределение на отрезке [a, b] и писать ξ
Î Ua,b (“ uniform”), если
ξ — координата точки, брошенной наудачу на отрезок [a, b]
числовой прямой. Это распределение можно задать и с помощью функции
распределения:
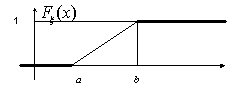
Пример 24. Будем говорить, что случайная величина ξ имеет
равномерное распределение на отрезке [a, b] и писать ξ
Î Ua,b (“ uniform”), если
ξ — координата точки, брошенной наудачу на отрезок [a, b]
числовой прямой. Это распределение можно задать и с помощью функции
распределения:
 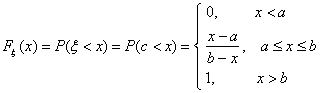
7.1 Свойства функции распределения
Теорема 19.
Функция распределения Fξ(x) обладает следующими свойствами:
F1) Функция распределения Fξ(x) не убывает: если
х1 < x2 то Fξ(x1)
< Fξ(x2);
F2) Существуют пределы
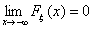 и и 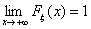 F3) Функция распределения Fξ(x) непрерывна слева:
F3) Функция распределения Fξ(x) непрерывна слева:
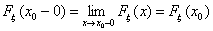 Теорема 20. Если функция F: R ® [0, 1] удовлетворяет
свойствам (F1)–(F3), то F есть функция распределения некоторой
случайной величины ξ, то есть найдется вероятностное пространство
(Ω, Ψ, Р) и случайная величина ξ на этом
пространстве, что F(х) = Fξ(x).
Теорема 20. Если функция F: R ® [0, 1] удовлетворяет
свойствам (F1)–(F3), то F есть функция распределения некоторой
случайной величины ξ, то есть найдется вероятностное пространство
(Ω, Ψ, Р) и случайная величина ξ на этом
пространстве, что F(х) = Fξ(x).
Прочие полезные свойства функций распределения
F4) В любой точке х0 разница Fξ(х0+0) - Fξ(х0) равна P(ξ = х0):
Следствие 3. Если функция распределения Fξ(x) непрерывна в точке х0, то
P(ξ = х0) = 0
F5) Для любой случайной величины ξ имеет место равенство
P(а £ ξ < b) = Fξ(a) - Fξ(b).
Если же функция распределения Fξ(x) непрерывна (для
любого x, или только в точках a и b), то
P(а £ ξ < b) = P(а < ξ < b) = P(а £ ξ
£ b) = P(а < ξ £ b) = Fξ(a) - Fξ
(b)
Функция распределения дискретного распределения
Мы уже видели, как выглядят функции распределения некоторых дискретных
распределений. Из свойств (F4), (F5) следует
Свойство 4. Случайная величина ξ имеет дискретное
распределение тогда и только тогда, когда функция распределения F
ξ — ступенчатая функция. При этом возможные значения ξ
— точки ai скачков Fξ, и
pi = P(ξ = ai ) = Fξ (ai + 0) - Fξ (ai )— величины скачков.
В следующей главе мы рассмотрим случайные величины, функции распределения
которых не удовлетворяют свойству 4 хотя бы потому, что они вовсе не имеют
разрывов. Более того, мы выделим класс функций распределения, которые
«восстанавливаются по своей производной» с помощью интегрирования (так
называемые абсолютно непрерывные функции).
Раздел 8. Абсолютно непрерывные распределения
Определение 28.Случайная величина ξ имеет называемые
абсолютно непрерывное распределение, если существует неотрицательная функция
fξ(x) такая, что для любого х Î R
функция распределения Fξ(x) представима в виде
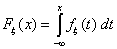 При этом функция fξ(x) называется плотностью
распределения случайной величины ξ.
Теорема 21.Плотность распределения обладает свойствами:
(f1) fξ(x)³ 0 для любого x;
(f2)
При этом функция fξ(x) называется плотностью
распределения случайной величины ξ.
Теорема 21.Плотность распределения обладает свойствами:
(f1) fξ(x)³ 0 для любого x;
(f2) 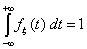 Эти два свойства полностью характеризуют класс плотностей:
Лемма 2. Если функция f обладает свойствами (f1) и (f2
), то существует вероятностное пространство и случайная величина ξ
на нем, для которой f является плотностью распределения.
Доказательство. Пусть Ω есть область, заключенная между осью абсцисс
и графиком функции f (« подграфик» функции f). Площадь
области Ω равна 1 по свойству (f2). И пусть случайная величина
ξ есть абсцисса точки, наудачу брошенной в эту область.
Тогда (вспомнить геометрическую вероятность) для любого х Î R
Эти два свойства полностью характеризуют класс плотностей:
Лемма 2. Если функция f обладает свойствами (f1) и (f2
), то существует вероятностное пространство и случайная величина ξ
на нем, для которой f является плотностью распределения.
Доказательство. Пусть Ω есть область, заключенная между осью абсцисс
и графиком функции f (« подграфик» функции f). Площадь
области Ω равна 1 по свойству (f2). И пусть случайная величина
ξ есть абсцисса точки, наудачу брошенной в эту область.
Тогда (вспомнить геометрическую вероятность) для любого х Î R
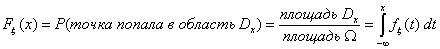 то есть f является плотностью распределения случайной величины ξ
то есть f является плотностью распределения случайной величины ξ
Свойства плотностей
(f3) Если случайная величина ξ имеет абсолютно непрерывное
распределение, то ее функция распределения всюду непрерывна.
Следствие 4. Если случайная величина ξ имеет абсолютно
непрерывное распределение, то P(ξ = х) = 0 для любого х
Î R.
(f4) Если случайная величина ξ имеет абсолютно непрерывное
распределение, то ее функция распределения дифференцируема почти всюду, и
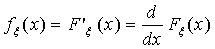 для почти всех х.
Замечание 12. Термин для «почти всех» означает «для всех, кроме
(возможно) х из некоторого множества нулевой меры (длины)». Заметьте,
что стоящую под интегралом функцию можно изменить в одной точке (или на
множестве нулевой длины), и интеграл (« площадь подграфика») от этого не
изменится.
(f5) Если случайная величина ξ имеет абсолютно непрерывное
распределение, то
для почти всех х.
Замечание 12. Термин для «почти всех» означает «для всех, кроме
(возможно) х из некоторого множества нулевой меры (длины)». Заметьте,
что стоящую под интегралом функцию можно изменить в одной точке (или на
множестве нулевой длины), и интеграл (« площадь подграфика») от этого не
изменится.
(f5) Если случайная величина ξ имеет абсолютно непрерывное
распределение, то
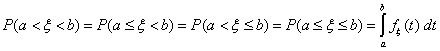 Доказательство. Действительно,
Доказательство. Действительно,
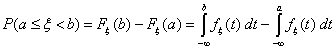 Остальные равенства вытекают из следствия 5.
Остальные равенства вытекают из следствия 5.
8.1 Примеры абсолютно непрерывных распределений
Равномерное.
Это распределение нам уже знакомо. Говорят, что ξ имеет равномерное
распределение на отрезке [a, b], и пишут ξ Î U
a,b если
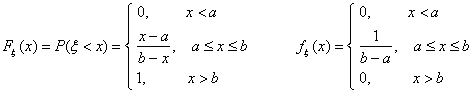 Заметьте, что в точках a и b функция распределения
недифференцируема, и плотность можно задать как угодно.
Показательное.
Говорят, что ξ имеет показательное распределение с параметром
α, α > 0 и ξ Î Еα
, если
Заметьте, что в точках a и b функция распределения
недифференцируема, и плотность можно задать как угодно.
Показательное.
Говорят, что ξ имеет показательное распределение с параметром
α, α > 0 и ξ Î Еα
, если
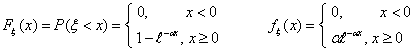 Показательное распределение является единственным абсолютно непрерывным
распределением, для которого выполнено свойство «не старения» (и в этом
смысле оно является непрерывным аналогом дискретного геометрического
распределения).
Теорема 21. Свойство «Не старения». Пусть ξ Î
Еα. Тогда для любых х, у > 0
Показательное распределение является единственным абсолютно непрерывным
распределением, для которого выполнено свойство «не старения» (и в этом
смысле оно является непрерывным аналогом дискретного геометрического
распределения).
Теорема 21. Свойство «Не старения». Пусть ξ Î
Еα. Тогда для любых х, у > 0
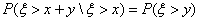 Нормальное.
Нормальное.
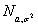 Говорят, что ξ
имеет нормальное распределение с параметрами а и σ2
, где а Î R, σ > 0, и пишут ξ
Î если ξ имеет следующую плотность распределения: Говорят, что ξ
имеет нормальное распределение с параметрами а и σ2
, где а Î R, σ > 0, и пишут ξ
Î если ξ имеет следующую плотность распределения:
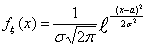 для любого x Î R
Убедимся, что fξ(x)действительно является плотностью
распределения. Так как fξ(x) > 0 для всех x
Î R, то свойство (f1) выполнено. Проверим выполнение (f2
). Используем табличный интеграл (интеграл Пуассона) для любого x Î R
Убедимся, что fξ(x)действительно является плотностью
распределения. Так как fξ(x) > 0 для всех x
Î R, то свойство (f1) выполнено. Проверим выполнение (f2
). Используем табличный интеграл (интеграл Пуассона)
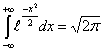 Нормальное (иначе называемое гауссовским по имени Карла Гаусса распределение
играет исключительно важную роль в теории вероятностей, поэтому мы очень
подробно изучим все свойства этого распределения.
Нормальное (иначе называемое гауссовским по имени Карла Гаусса распределение
играет исключительно важную роль в теории вероятностей, поэтому мы очень
подробно изучим все свойства этого распределения.
8.2 Свойства нормального распределения
Нормальное распределение задается, как мы видим, с помощью плотности
распределения. Связано это с тем, что нельзя выписать первообразную от функции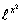 иначе как в виде интеграла, поэтому функцию распределения этого закона можно
записать лишь в таком виде:
иначе как в виде интеграла, поэтому функцию распределения этого закона можно
записать лишь в таком виде:
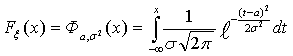
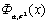 Мы часто будем использовать
обозначение для функции распределения нормального распределения с параметрами
а и σ2. Мы часто будем использовать
обозначение для функции распределения нормального распределения с параметрами
а и σ2.
Стандартное нормальное распределение
Нормальное распределение при 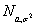 а = 0 и σ= 1 называется стандартным нормальным распределением.
Плотность стандартного нормального распределения имеет вид
а = 0 и σ= 1 называется стандартным нормальным распределением.
Плотность стандартного нормального распределения имеет вид
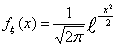 для любого x Î R
а функция распределения для любого x Î R
а функция распределения
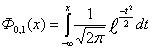 табулирована (то есть ее значения вычислены при многих х) почти во всех
математических справочниках. Установим связь между
табулирована (то есть ее значения вычислены при многих х) почти во всех
математических справочниках. Установим связь между
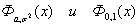 Свойство 5. Для любого x Î R справедливо соотношение
Свойство 5. Для любого x Î R справедливо соотношение
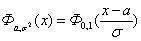 То же самое на языке случайных величин можно сформулировать так:
То же самое на языке случайных величин можно сформулировать так:
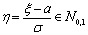 Следствие 5. Если Следствие 5. Если 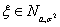 то
Следствие 6. Если то
Следствие 6. Если 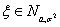 то то
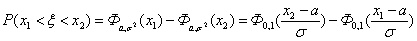 Как мы видим, вычисление любых вероятностей для нормально распределенной
случайной величины сводится к вычислению функции распределения Ф
0,1. Ее свойства
Свойство 6. Ф0,1(0) = 0,5
Свойство 7. Ф0,1(-х) = 1 - Ф0,1(х)
Свойство 8. Если ξ Î N0,1, то
Как мы видим, вычисление любых вероятностей для нормально распределенной
случайной величины сводится к вычислению функции распределения Ф
0,1. Ее свойства
Свойство 6. Ф0,1(0) = 0,5
Свойство 7. Ф0,1(-х) = 1 - Ф0,1(х)
Свойство 8. Если ξ Î N0,1, то
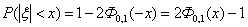 Свойство 9 (« Правило трех сигм»).
Если
Свойство 9 (« Правило трех сигм»).
Если 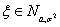 то то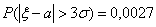 Смысла в запоминании числа 0.0027 нет никакого, а вот помнить, что почти вся
масса нормального распределения сосредоточена в границах [a - 3σ, a -
3σ] всегда полезно.
Смысла в запоминании числа 0.0027 нет никакого, а вот помнить, что почти вся
масса нормального распределения сосредоточена в границах [a-3σ,
a+3σ], всегда полезно.
Смысла в запоминании числа 0.0027 нет никакого, а вот помнить, что почти вся
масса нормального распределения сосредоточена в границах [a - 3σ, a -
3σ] всегда полезно.
Смысла в запоминании числа 0.0027 нет никакого, а вот помнить, что почти вся
масса нормального распределения сосредоточена в границах [a-3σ,
a+3σ], всегда полезно.
Раздел 9. Случайные вектора и их распределения
Определение 29. Если случайные величины 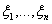 заданы на одном вероятностном пространстве, то вектор (
заданы на одном вероятностном пространстве, то вектор (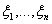 ) мы будем называть случайным вектором.
Определение 30. Функция
) мы будем называть случайным вектором.
Определение 30. Функция 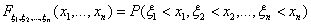 называется функцией распределения случайного вектора (
называется функцией распределения случайного вектора (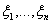 ) или функцией совместного распределения случайных величин
) или функцией совместного распределения случайных величин 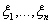 .
.
9.1 Свойства функции совместного распределения
Для простоты обозначений все дальнейшие рассуждения и формулировки приводятся в
случае n = 2 для случайного вектора (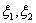 )
F0)
)
F0) 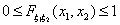 F1)
F1) 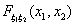 не убывает по каждой координате вектора (x1 x2).
F2) Для любого i = 1, 2, существуют не убывает по каждой координате вектора (x1 x2).
F2) Для любого i = 1, 2, существуют
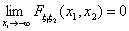
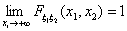 При этом
При этом
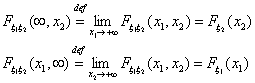 F3) Функция
F3) Функция 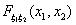 по каждой координате вектора (x1 x2) непрерывна слева.
Только теперь этих свойств оказывается недостаточно для описания класса функций
совместного распределения. Иначе говоря, выполнение этих свойств для некоторой
функции F: R2 ® R вовсе не гарантирует, что
эта функция является функцией распределения некоторого случайного вектора.
Пример 25. Функция по каждой координате вектора (x1 x2) непрерывна слева.
Только теперь этих свойств оказывается недостаточно для описания класса функций
совместного распределения. Иначе говоря, выполнение этих свойств для некоторой
функции F: R2 ® R вовсе не гарантирует, что
эта функция является функцией распределения некоторого случайного вектора.
Пример 25. Функция

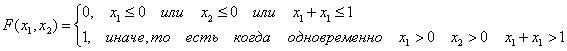 a) удовлетворяет всем свойствам (F0)-(F3);
б) не является функцией распределения никакого вектора (ξ1
, ξ2.) хотя бы потому, что, найдись такой вектор,
найдется и прямоугольник [a1 b1] x [a2
b2], вероятность попасть в который (вычисленная с помощью этой
«функции распределения») отрицательна:
P(a1 £ ξ1< b1 , a2 £ ξ2<b2 ) < 0!
Как же связана вероятность вектору попасть в прямоугольник с функцией
распределения этого вектора?
Упражнение. Доказать, что
P(a1 £ ξ1< b1 , a2
£ ξ2<b2 )= F ξ1
ξ2 (b1, b2) - F ξ
1 ξ2 (a1, b2) - F
ξ1 ξ2 (b1, a2
) + F ξ1 ξ2 (a1
, a2) (8)
Оказывается, если потребовать дополнительно от функции F, чтобы для всякого
[a1 b1] x [a2 b2]
вероятность P(a1 £ ξ1< b1]
, [a2 £ ξ2<b2], связанная
с функцией F равенством (8), была неотрицательна, то любая функция, обладающая
этим свойством и свойствами (F0)-(F3), уже будет функцией
распределения некоторого случайного вектора.
a) удовлетворяет всем свойствам (F0)-(F3);
б) не является функцией распределения никакого вектора (ξ1
, ξ2.) хотя бы потому, что, найдись такой вектор,
найдется и прямоугольник [a1 b1] x [a2
b2], вероятность попасть в который (вычисленная с помощью этой
«функции распределения») отрицательна:
P(a1 £ ξ1< b1 , a2 £ ξ2<b2 ) < 0!
Как же связана вероятность вектору попасть в прямоугольник с функцией
распределения этого вектора?
Упражнение. Доказать, что
P(a1 £ ξ1< b1 , a2
£ ξ2<b2 )= F ξ1
ξ2 (b1, b2) - F ξ
1 ξ2 (a1, b2) - F
ξ1 ξ2 (b1, a2
) + F ξ1 ξ2 (a1
, a2) (8)
Оказывается, если потребовать дополнительно от функции F, чтобы для всякого
[a1 b1] x [a2 b2]
вероятность P(a1 £ ξ1< b1]
, [a2 £ ξ2<b2], связанная
с функцией F равенством (8), была неотрицательна, то любая функция, обладающая
этим свойством и свойствами (F0)-(F3), уже будет функцией
распределения некоторого случайного вектора.
9.2 Типы многомерных распределений
Ограничимся рассмотрением только двух случаев, когда совместное распределение
координат случайного вектора (ξ1, ξ2.)
либо дискретно, либо абсолютно непрерывно.
Дискретное совместное распределение
Определение 31. Говорят, что случайные величины ξ1
, ξ2. имеют дискретное, совместное
распределение, если существует конечный или счетный набор { ai
, bi } такой, что
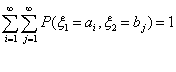 Таблицу, на пересечении i-й строки и j-го столбца которой (или
наоборот) стоит число
P(ξ1= ai ,ξ2=
bj) называют таблицей совместного распределения случайных
величин ξ1,. ξ2
Замечание 13. Напомню, что таблицы распределения каждой из случайных
величин ξ1, ξ2 в отдельности
(таблицы частных, или маргинальных распределений) восстанавливаются по
таблице совместного распределения с помощью очевидных формул:
Таблицу, на пересечении i-й строки и j-го столбца которой (или
наоборот) стоит число
P(ξ1= ai ,ξ2=
bj) называют таблицей совместного распределения случайных
величин ξ1,. ξ2
Замечание 13. Напомню, что таблицы распределения каждой из случайных
величин ξ1, ξ2 в отдельности
(таблицы частных, или маргинальных распределений) восстанавливаются по
таблице совместного распределения с помощью очевидных формул:
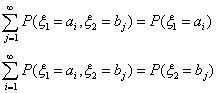 Если эти формулы вам не представляются очевидными, необходимо вернуться к
разделу 4 и перечитать определение 18 полной группы событий,
обратив также внимание на доказательство теоремы 8 (формулы полной
вероятности).
Если эти формулы вам не представляются очевидными, необходимо вернуться к
разделу 4 и перечитать определение 18 полной группы событий,
обратив также внимание на доказательство теоремы 8 (формулы полной
вероятности).
Абсолютно непрерывное совместное распределение
Определение 32. Говорят, что с.в. ξ1, ξ
2 (заданные на одном вероятностном пространстве) имеют абсолютно
непрерывное совместное распределение, если существует функция 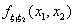 такая, что для любой точки (x1, x2) Î
R2
такая, что для любой точки (x1, x2) Î
R2
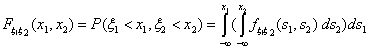 Если такая функция
Если такая функция 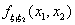 существует, она называется плотностью совместного распределения
случайных величин ξ1, ξ2.
Замечание 14. Для всего дальнейшего более чем достаточно считать, что
существует, она называется плотностью совместного распределения
случайных величин ξ1, ξ2.
Замечание 14. Для всего дальнейшего более чем достаточно считать, что
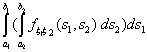 равняется объему под графиком функции f над областью интегрирования —
прямоугольником [a1,b1] x [a2,b
2].
Плотность совместного распределения обладает свойствами, аналогичными
свойствам плотности распределения одной случайной величины:
(f1)
равняется объему под графиком функции f над областью интегрирования —
прямоугольником [a1,b1] x [a2,b
2].
Плотность совместного распределения обладает свойствами, аналогичными
свойствам плотности распределения одной случайной величины:
(f1) 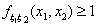 для любых x1, x2 Î R;
(f2) для любых x1, x2 Î R;
(f2) 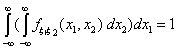 .
Более того, любая функция, обладающая этими свойствами, является плотностью
некоторого совместного распределения.
Если совместное распределение абсолютно непрерывно, то по функции совместного
распределения его плотность находится как смешанная частная производная:
(f3) .
Более того, любая функция, обладающая этими свойствами, является плотностью
некоторого совместного распределения.
Если совместное распределение абсолютно непрерывно, то по функции совместного
распределения его плотность находится как смешанная частная производная:
(f3) 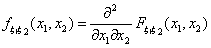 .
Из свойства (F2) функции совместного распределения вытекает следующее
утверждение. Для n > 2 это утверждение, как и свойство (F2),
выглядит существенно иначе!
Теорема 22. Если случайные величины ξ1,
ξ2 имеют абсолютно непрерывное совместное распределение с
плотностью f (x1, x2), то
ξ1, и ξ2 в отдельности также имеют
абсолютно непрерывное распределение с плотностями: .
Из свойства (F2) функции совместного распределения вытекает следующее
утверждение. Для n > 2 это утверждение, как и свойство (F2),
выглядит существенно иначе!
Теорема 22. Если случайные величины ξ1,
ξ2 имеют абсолютно непрерывное совместное распределение с
плотностью f (x1, x2), то
ξ1, и ξ2 в отдельности также имеют
абсолютно непрерывное распределение с плотностями:
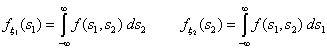
9.3 Независимость случайных величин
Определение 33. Случайные величины ξ1, ξ
2, . , ξn независимы, если для любого набора
множеств В1 Í R, . Вn Í R
имеет место равенство:
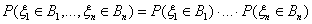 Это определение можно сформулировать в терминах функций распределения:
Определение 34. Случайные величины ξ1, ξ
2, . , ξn независимы, если для любых х
1, х2, . , хn имеет место
равенство:
Это определение можно сформулировать в терминах функций распределения:
Определение 34. Случайные величины ξ1, ξ
2, . , ξn независимы, если для любых х
1, х2, . , хn имеет место
равенство:
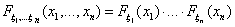 Определение 35. Случайные величины ξ1, ξ
2, . , ξn с дискретным распределением
независимы, если для любых а1, а2, . ,
аn имеет место равенство:
Определение 35. Случайные величины ξ1, ξ
2, . , ξn с дискретным распределением
независимы, если для любых а1, а2, . ,
аn имеет место равенство:
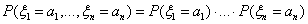 Для случайных величин с абсолютно непрерывным совместным распределением
определение независимости можно сформулировать так:
Определение 36. Случайные величины ξ1, ξ
2, . , ξn с абсолютно непрерывным совместным
распределением независимы, если плотность совместного распределения
равна произведению плотностей случайных ξ1, ξ
2, . , ξn, то есть для любых х1
, х2, . , хn имеет место равенство:
Для случайных величин с абсолютно непрерывным совместным распределением
определение независимости можно сформулировать так:
Определение 36. Случайные величины ξ1, ξ
2, . , ξn с абсолютно непрерывным совместным
распределением независимы, если плотность совместного распределения
равна произведению плотностей случайных ξ1, ξ
2, . , ξn, то есть для любых х1
, х2, . , хn имеет место равенство:
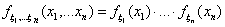
Раздел 10. Преобразования случайных величин 10.1 Преобразование
одной случайной величины
Мы будем рассматривать только преобразования случайных величин с абсолютно
непрерывными распределениями. Пусть с. в. ξ имеет функцию
распределения Fξ(x) и плотность распределения f
ξ(x). Построим с помощью функции g: R ® R
случайную величину η= g(ξ). Требуется найти
функцию распределения и, если существует, плотность распределения η
.
Замечание 15. Плотность распределения случайной величины η=
g(ξ) существует далеко не при любых функциях g. Так,
если функция g кусочно-постоянна, то с. в. η имеет
дискретное распределение, и плотность ее распределения не существует.
Плотность распределения g(ξ) заведомо существует, если,
например, функция g(ξ) монотонна («строго монотонна»).
Вспомним, что означает «найти плотность распределения η, если она
существует».
По определению, если мы представим (для любого х) функцию распределения
η в виде 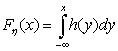 где
подинтегральная функция h(y) неотрицательна, то плотность распределения с.в.
η существует и в точности равна подинтегральной функции fξ
(x) = h(x) . где
подинтегральная функция h(y) неотрицательна, то плотность распределения с.в.
η существует и в точности равна подинтегральной функции fξ
(x) = h(x) .
Так что доказывать существование плотности распределения и находить ее мы
будем одновременно, находя нужное интегральное представление для функции
распределения.
Теорема 23. Пусть ξ имеет функцию распределения F
ξ(x) и плотность распределения fξ(x) , и
постоянная a отлична от нуля. Тогда случайная величина η = a
ξ + b имеет плотность распределения
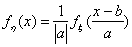 Для произвольной монотонной функции g (то есть либо монотонно
возрастающей функции, либо монотонно убывающей функции справедливо аналогичное
теореме 23 утверждение).
Теорема 24. Пусть ξ имеет функцию распределения F
ξ(x) и плотность распределения fξ(x), и
функция g: R ® R монотонна. Тогда случайная величина
η= g(ξ) имеет плотность распределения
Для произвольной монотонной функции g (то есть либо монотонно
возрастающей функции, либо монотонно убывающей функции справедливо аналогичное
теореме 23 утверждение).
Теорема 24. Пусть ξ имеет функцию распределения F
ξ(x) и плотность распределения fξ(x), и
функция g: R ® R монотонна. Тогда случайная величина
η= g(ξ) имеет плотность распределения
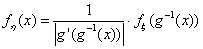 Здесь g -1— функция, обратная к g, и
Здесь g -1— функция, обратная к g, и
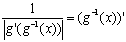 — производная функции g -1.
Следствие 7. Если ξ Î N0,1, то η = σξ+а Î — производная функции g -1.
Следствие 7. Если ξ Î N0,1, то η = σξ+а Î 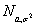 Следствие 8. Если η Î
Следствие 8. Если η Î 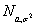 , то ξ = (η –а)/ σ Î N0,1.
Следствие 9. Если ξ Î Еα, то η = αξÎ Е1 , то ξ = (η –а)/ σ Î N0,1.
Следствие 9. Если ξ Î Еα, то η = αξÎ Е1
10.2 Функции от двух случайных величин
Пусть ξ1 ξ2 — случайные величины с
плотностью совместного распределения 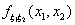 , и задана функция g : R2 ® R. Требуется
найти функцию (а если существует, то и плотность) распределения случайной
величины η = g(ξ1 , ξ2
).
Пользуясь тем, что вероятность случайному вектору попасть в область можно
вычислить как объем под графиком плотности распределения вектора над этой
областью, сформулируем утверждение.
Теорема 25. Пусть хÎ R, и область D
x Î R2 состоит из точек (x1 x
2 ) таких, что g (x1 x2 ) <
x. Тогда случайная величина η = g(ξ1
, ξ2). имеет функцию распределения
, и задана функция g : R2 ® R. Требуется
найти функцию (а если существует, то и плотность) распределения случайной
величины η = g(ξ1 , ξ2
).
Пользуясь тем, что вероятность случайному вектору попасть в область можно
вычислить как объем под графиком плотности распределения вектора над этой
областью, сформулируем утверждение.
Теорема 25. Пусть хÎ R, и область D
x Î R2 состоит из точек (x1 x
2 ) таких, что g (x1 x2 ) <
x. Тогда случайная величина η = g(ξ1
, ξ2). имеет функцию распределения
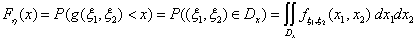 Всюду далее в этой главе предполагается, что случайные величины ξ1
и ξ2 независимы, то есть
Всюду далее в этой главе предполагается, что случайные величины ξ1
и ξ2 независимы, то есть 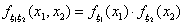 Следствие 10 (Формула свертки). Если с. в. ξ1 и
ξ2 независимы и имеют абсолютно непрерывное распределение с
плотностями f ξ1 (x1) и
f ξ2 (x2)., то плотность
распределения суммы ξ1 + ξ2
равна «свертке» плотностей f ξ1 (x1
) и f ξ2 (x2)
Следствие 10 (Формула свертки). Если с. в. ξ1 и
ξ2 независимы и имеют абсолютно непрерывное распределение с
плотностями f ξ1 (x1) и
f ξ2 (x2)., то плотность
распределения суммы ξ1 + ξ2
равна «свертке» плотностей f ξ1 (x1
) и f ξ2 (x2)
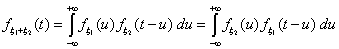 (9)
Следствие 10 не только предлагает формулу для вычисления плотности
распределения суммы, но и утверждает (заметьте!), что сумма двух независимых
случайных величин с абсолютно непрерывными распределениями также имеет
абсолютно непрерывное распределение.
Если даже одна из двух независимых случайных величин имеет дискретное, а
вторая – абсолютно непрерывное распределение, то их сумма тоже имеет
абсолютно непрерывное распределение, как показывает следующее упражнение.
Упражнение. Пусть с. в. ξ имеет таблицу распределения P
(ξ = аi) = pi, с. в. η имеет
плотность распределения fη(x), и эти величины
независимы. Доказать, что ξ +η имеет плотность
распределения
(9)
Следствие 10 не только предлагает формулу для вычисления плотности
распределения суммы, но и утверждает (заметьте!), что сумма двух независимых
случайных величин с абсолютно непрерывными распределениями также имеет
абсолютно непрерывное распределение.
Если даже одна из двух независимых случайных величин имеет дискретное, а
вторая – абсолютно непрерывное распределение, то их сумма тоже имеет
абсолютно непрерывное распределение, как показывает следующее упражнение.
Упражнение. Пусть с. в. ξ имеет таблицу распределения P
(ξ = аi) = pi, с. в. η имеет
плотность распределения fη(x), и эти величины
независимы. Доказать, что ξ +η имеет плотность
распределения
 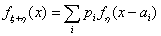
10.3 Примеры использования формулы свертки
Пример 26. Пусть независимые случайные величины ξ и
η имеют стандартное нормальное распределение. Докажем, что их сумма
имеет нормальное распределение с параметрами 0 и 2.
Доказательство. По формуле свертки, плотность суммы равна
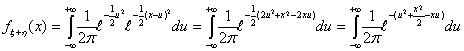 Выделим полный квадрат по u в показателе экспоненты:
Выделим полный квадрат по u в показателе экспоненты:
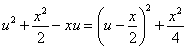 Тогда
Тогда
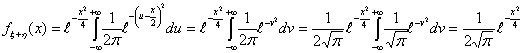 Последнее равенство верно поскольку под интегралом стоит плотность нормального
распределения с параметрами 0 и
Последнее равенство верно поскольку под интегралом стоит плотность нормального
распределения с параметрами 0 и 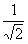 , так что интеграл по всей прямой равен 1. Итак, мы получили, что плотность
суммы есть плотность нормального распределения с параметрами 0 и 2.
Если сумма двух независимых случайных величин из одного и того же распределения
(возможно, с разными параметрами) имеет такое же распределение, говорят, что
это распределение устойчиво относительно суммирования.
В следующих утверждениях, перечислены практически все устойчивые распределения.
Лемма 3. Пусть случайные величины ξ Î П
λ и ηÎ Пμ независимы. Тогда
ξ+ η Î Пλ+μ
Лемма 4. Пусть случайные величины ξ Î Bn
,p и ξ Î Bm,
p независимы. Тогда ξ+ η Î Bm
+n,p
Лемма 5. Пусть случайные величины
, так что интеграл по всей прямой равен 1. Итак, мы получили, что плотность
суммы есть плотность нормального распределения с параметрами 0 и 2.
Если сумма двух независимых случайных величин из одного и того же распределения
(возможно, с разными параметрами) имеет такое же распределение, говорят, что
это распределение устойчиво относительно суммирования.
В следующих утверждениях, перечислены практически все устойчивые распределения.
Лемма 3. Пусть случайные величины ξ Î П
λ и ηÎ Пμ независимы. Тогда
ξ+ η Î Пλ+μ
Лемма 4. Пусть случайные величины ξ Î Bn
,p и ξ Î Bm,
p независимы. Тогда ξ+ η Î Bm
+n,p
Лемма 5. Пусть случайные величины 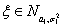 и и 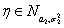 независимы. Тогда независимы. Тогда 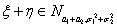 Показательное распределение не устойчиво по суммированию, однако его можно
считать частным случаем гамма-распределения, которое уже в некотором смысле
устойчиво относительно суммирования.
Определение 37. Случайная величина ξ имеет
гамма-распределение Гα,λ с параметрами α >
0, λ > 0, если она имеет плотность распределения
Показательное распределение не устойчиво по суммированию, однако его можно
считать частным случаем гамма-распределения, которое уже в некотором смысле
устойчиво относительно суммирования.
Определение 37. Случайная величина ξ имеет
гамма-распределение Гα,λ с параметрами α >
0, λ > 0, если она имеет плотность распределения
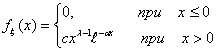 где постоянная c вычисляется из условия
где постоянная c вычисляется из условия
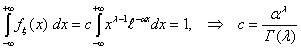 Заметим, что показательное распределение Еα есть
гамма-распределение Гα,1.
Лемма 6. Пусть независимые случайные величины ξ1,
. , ξn имеют показательное распределение Е
α = Гα,1 Тогда ξ1
+.+ξn Î Гα,n
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть
случайная величина мы всегда в праве от нее что-нибудь ожидать.»
Из студенческой контрольной работы.
Заметим, что показательное распределение Еα есть
гамма-распределение Гα,1.
Лемма 6. Пусть независимые случайные величины ξ1,
. , ξn имеют показательное распределение Е
α = Гα,1 Тогда ξ1
+.+ξn Î Гα,n
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть
случайная величина мы всегда в праве от нее что-нибудь ожидать.»
Из студенческой контрольной работы.
Раздел 11. Числовые характеристики случайных величин 11.1
Математическое ожидание случайной величины
Определение 38. Математическим ожиданием Eξ (средним
значением, первым моментом) случайной величины ξ с дискретным
распределением, задаваемым таблицей P(ξ = аi) = pi
, называется число
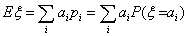 если указанный ряд абсолютно сходится.
Если же если указанный ряд абсолютно сходится.
Если же
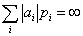 , то говорят, что математическое ожидание не существует.
Определение 39. Математическим ожиданием Eξ
случайной величины ξ с абсолютно непрерывным распределением с
плотностью распределения fξ(x), называется число , то говорят, что математическое ожидание не существует.
Определение 39. Математическим ожиданием Eξ
случайной величины ξ с абсолютно непрерывным распределением с
плотностью распределения fξ(x), называется число
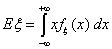 если указанный интеграл абсолютно сходится.
Если же если указанный интеграл абсолютно сходится.
Если же
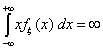 , то говорят, что математическое ожидание не существует.
Математическое ожидание имеет простой физический смысл: если на прямой
разместить единичную массу, поместив в точку аi массу p
i (для дискретного распределения), или «размазав» ее с плотностью
fξ(x) (для абсолютно непрерывного распределения), то точка E
ξ есть координата «центра тяжести» прямой.
Пример 26. Пусть случайная величина ξ равна числу очков,
выпадающих при одном подбрасывании кубика. Тогда , то говорят, что математическое ожидание не существует.
Математическое ожидание имеет простой физический смысл: если на прямой
разместить единичную массу, поместив в точку аi массу p
i (для дискретного распределения), или «размазав» ее с плотностью
fξ(x) (для абсолютно непрерывного распределения), то точка E
ξ есть координата «центра тяжести» прямой.
Пример 26. Пусть случайная величина ξ равна числу очков,
выпадающих при одном подбрасывании кубика. Тогда
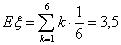
 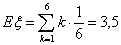 в среднем при подбрасывании кубика выпадает 3.5 очка
Пример 27. Пусть случайная величина ξ — координата точки,
брошенной наудачу на отрезок [a,b]. Тогда
в среднем при подбрасывании кубика выпадает 3.5 очка
Пример 27. Пусть случайная величина ξ — координата точки,
брошенной наудачу на отрезок [a,b]. Тогда
 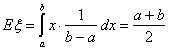 центр тяжести равномерного распределения на отрезке есть середина отрезка.
центр тяжести равномерного распределения на отрезке есть середина отрезка.
11.2 Свойства математического ожидания
Во всех свойствах предполагается, что рассматриваемые математические ожидания
существуют.
E0. Математическое ожидание случайной величины есть ЧИСЛО!
E1. Для произвольной функции функция g : R ® R
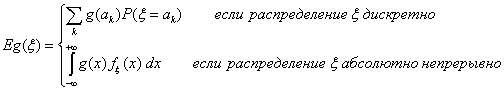 Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
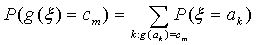 Тогда
Тогда
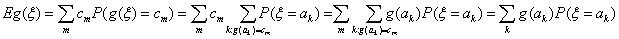 E2 Математическое ожидание const равно этой const Eс = с.
E3. const можно вынести за знак математического
ожидания: E(с ξ) = с Eξ.
Доказательство. Следует из свойства E1 при g(ξ) = с ξ .
E4. Математическое ожидание суммы любых случайных величин ξ и
η равно сумме их математических ожиданий.
E (ξ + η ) = E (ξ )+ E (η)
Доказательство. Для величин с дискретным распределением: пусть x
k и yn — значения ξ и η,
соответственно.
E2 Математическое ожидание const равно этой const Eс = с.
E3. const можно вынести за знак математического
ожидания: E(с ξ) = с Eξ.
Доказательство. Следует из свойства E1 при g(ξ) = с ξ .
E4. Математическое ожидание суммы любых случайных величин ξ и
η равно сумме их математических ожиданий.
E (ξ + η ) = E (ξ )+ E (η)
Доказательство. Для величин с дискретным распределением: пусть x
k и yn — значения ξ и η,
соответственно.
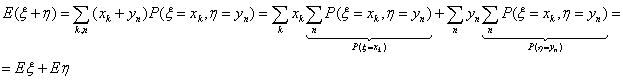 E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
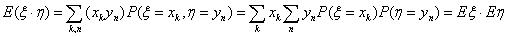 Замечание 16. Обратное утверждение к свойству E6 неверно: из
равенства E(ξη) = Eξ Eη. Не
следует независимость величин ξ и η.
Пример 28. Пусть φ Î U0,2π
, ξ = cos φ, η = sin φ— заведомо зависимые случайные
величины. Но математическое ожидание их произведения равно произведению их
математических ожиданий: по свойству E1
Замечание 16. Обратное утверждение к свойству E6 неверно: из
равенства E(ξη) = Eξ Eη. Не
следует независимость величин ξ и η.
Пример 28. Пусть φ Î U0,2π
, ξ = cos φ, η = sin φ— заведомо зависимые случайные
величины. Но математическое ожидание их произведения равно произведению их
математических ожиданий: по свойству E1
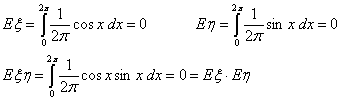
11.3 Моменты старших порядков. Дисперсия
Определение 40. Если 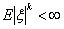 , то число , то число
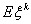 называется моментом порядка k (k -м моментом) случайной величины ξ; называется моментом порядка k (k -м моментом) случайной величины ξ;
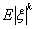 называется
абсолютным моментом порядка k (абсолютным k -м моментом) случайной
величины ξ; называется
абсолютным моментом порядка k (абсолютным k -м моментом) случайной
величины ξ;
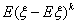 называется
центральным моментом порядка k (центральным k -м моментом) случайной
величины ξ; называется
центральным моментом порядка k (центральным k -м моментом) случайной
величины ξ;
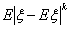 называется
абсолютным центральным моментом порядка k (абсолютным центральным k
-м моментом) случайной величины ξ.
Число Dξ = E(ξ – Eξ)2
(центральный момент порядка 2) называется дисперсией случайной величины
ξ
Пример 29. Пусть, скажем, случайная величина ξ принимает
значение 0 с вероятностью 1-10-5 , и значение 100 с вероятностью 10
-5. Посмотрим, как моменты разных порядков реагируют на большие, но
маловероятные значения случайной величины. называется
абсолютным центральным моментом порядка k (абсолютным центральным k
-м моментом) случайной величины ξ.
Число Dξ = E(ξ – Eξ)2
(центральный момент порядка 2) называется дисперсией случайной величины
ξ
Пример 29. Пусть, скажем, случайная величина ξ принимает
значение 0 с вероятностью 1-10-5 , и значение 100 с вероятностью 10
-5. Посмотрим, как моменты разных порядков реагируют на большие, но
маловероятные значения случайной величины.
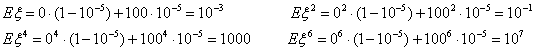 Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число
Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число 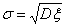 называют среднеквадратичным отклонением случайной величины ξ
.
Следует хорошо понимать, что из существования моментов больших порядков
следует существование моментов меньших порядков. В частности, конечность
второго момента (или дисперсии) влечет существование математического
ожидания.
называют среднеквадратичным отклонением случайной величины ξ
.
Следует хорошо понимать, что из существования моментов больших порядков
следует существование моментов меньших порядков. В частности, конечность
второго момента (или дисперсии) влечет существование математического
ожидания.
11.4 Свойства дисперсии
Все свойства дисперсии следуют из соответствующих свойств математического
ожидания.
D1. 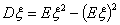 Действительно,
Действительно,
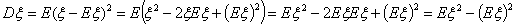 D2.
D2. 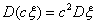 D3.
D3.
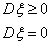 если и только если ξ= const.п.н.
Доказательство. Дисперсия есть всего-навсего математическое ожидание п.н.
неотрицательной с.в.:
Dξ = E(ξ – Eξ)2, и
неотрицательность дисперсии следует из свойства E5. По тому же свойству, D
ξ = 0 если и только если E(ξ – Eξ)2
= 0 п.н., то есть ξ = ξ п.н.
D4. Дисперсия не меняется от сдвига с.в. на постоянную: если и только если ξ= const.п.н.
Доказательство. Дисперсия есть всего-навсего математическое ожидание п.н.
неотрицательной с.в.:
Dξ = E(ξ – Eξ)2, и
неотрицательность дисперсии следует из свойства E5. По тому же свойству, D
ξ = 0 если и только если E(ξ – Eξ)2
= 0 п.н., то есть ξ = ξ п.н.
D4. Дисперсия не меняется от сдвига с.в. на постоянную:
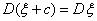 D5. Если ξ и η независимы, то
D5. Если ξ и η независимы, то
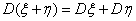 Действительно,
Действительно,
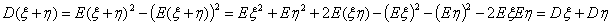 так как математическое ожидание произведения независимых с.в. равно
произведению их математических ожиданий.
D6. Минимум среднеквадратического отклонения случайной величины
ξ от точек вещественной прямой есть среднеквадратическое отклонение
ξ от своего математического ожидания:
так как математическое ожидание произведения независимых с.в. равно
произведению их математических ожиданий.
D6. Минимум среднеквадратического отклонения случайной величины
ξ от точек вещественной прямой есть среднеквадратическое отклонение
ξ от своего математического ожидания:
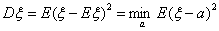 Наименьший момент инерции стержня с распределенной на нем единичной массой
получится, если точка вращения – центр тяжести стержня, а не любая другая
точка.
Доказательство.
Наименьший момент инерции стержня с распределенной на нем единичной массой
получится, если точка вращения – центр тяжести стержня, а не любая другая
точка.
Доказательство.
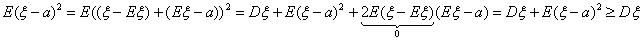 причем равенство достигается только для а = Eξ.
11.5 Математические ожидания и дисперсии стандартных распределений
Пример 31. Распределение Бернулли Вр,
причем равенство достигается только для а = Eξ.
11.5 Математические ожидания и дисперсии стандартных распределений
Пример 31. Распределение Бернулли Вр,
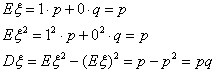 Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
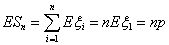 так как все ξi одинаково распределены и их
математическое ожидание равно pi;
так как все ξi одинаково распределены и их
математическое ожидание равно pi;
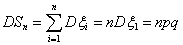 поскольку ξi независимы и дисперсия каждой равна pq.
Пример 33. Геометрическое распределение Gp
При p Î (0,1)
поскольку ξi независимы и дисперсия каждой равна pq.
Пример 33. Геометрическое распределение Gp
При p Î (0,1)
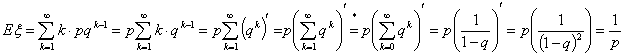 Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
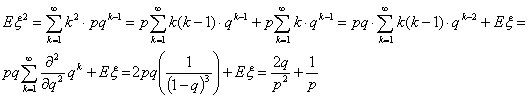 Поэтому
Пример 34. Распределение Пуассона Пλ
Поэтому
Пример 34. Распределение Пуассона Пλ

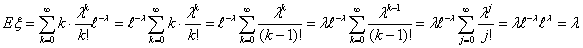 Показать, что
Показать, что
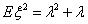 , следовательно , следовательно 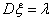 Пример 35. Равномерное распределение Ua,b
Пример 35. Равномерное распределение Ua,b
 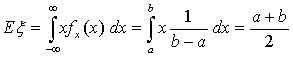
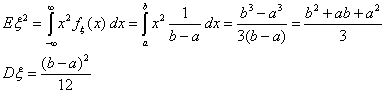 Пример 36. Стандартное нормальное распределение N0,1
Пример 36. Стандартное нормальное распределение N0,1
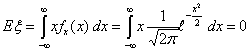 поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей
поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей 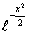 Последнее равенство следует из того, что
а интеграл по всей прямой от плотности любого распределения равен 1. Поэтому
Пример 37. Нормальное распределение
Последнее равенство следует из того, что
а интеграл по всей прямой от плотности любого распределения равен 1. Поэтому
Пример 37. Нормальное распределение  Мы знаем, что если
Мы знаем, что если
 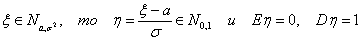 Поэтому
Поэтому
 Пример 38. Показательное (экспоненциальное) распределение Еα
Найдем для произвольного k Î N момент порядка k.
Пример 38. Показательное (экспоненциальное) распределение Еα
Найдем для произвольного k Î N момент порядка k.
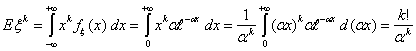 В последнем равенстве мы воспользовались гамма-функцией Эйлера:
В последнем равенстве мы воспользовались гамма-функцией Эйлера:
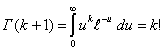 Соответственно, Соответственно,
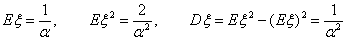 Пример 39. Стандартное распределение Коши С0,1
Распределение Коши. Говорят, что ξ имеет распределение Коши с
параметрами α, σ2, где α Î
R, σ > 0, если
Пример 39. Стандартное распределение Коши С0,1
Распределение Коши. Говорят, что ξ имеет распределение Коши с
параметрами α, σ2, где α Î
R, σ > 0, если
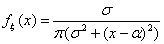 для всех х Î R
Распределение Коши имеет, например, абсцисса точки пересечения луча, посланного
из точки (α, σ) под наудачу выбранным углом, для всех х Î R
Распределение Коши имеет, например, абсцисса точки пересечения луча, посланного
из точки (α, σ) под наудачу выбранным углом,
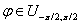 с осью ОХ.
Математическое ожидание для распределения Коши не существует, поскольку с осью ОХ.
Математическое ожидание для распределения Коши не существует, поскольку
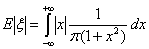 расходится (подинтегральная функция ведет себя на бесконечности как 1/х).
Пример 40. Распределение Парето
Распределение Парето. Говорят, что ξ имеет распределение Парето с
параметрами х0, s, где х0 > 0,
s > 0, если
расходится (подинтегральная функция ведет себя на бесконечности как 1/х).
Пример 40. Распределение Парето
Распределение Парето. Говорят, что ξ имеет распределение Парето с
параметрами х0, s, где х0 > 0,
s > 0, если
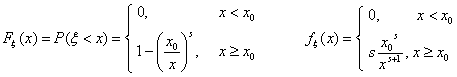 У распределения Парето существуют только моменты порядка u < s, поскольку
У распределения Парето существуют только моменты порядка u < s, поскольку
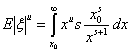 сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть
случайная величина мы всегда в праве от нее что-нибудь ожидать.»
Из студенческой контрольной работы.
сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть
случайная величина мы всегда в праве от нее что-нибудь ожидать.»
Из студенческой контрольной работы.
Раздел 11. Числовые характеристики случайных величин 11.1
Математическое ожидание случайной величины
Определение 38. Математическим ожиданием Eξ (средним
значением, первым моментом) случайной величины ξ с дискретным
распределением, задаваемым таблицей P(ξ = аi) = pi
, называется число
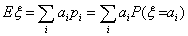 если указанный ряд абсолютно сходится.
Если же если указанный ряд абсолютно сходится.
Если же
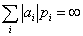 , то говорят, что математическое ожидание не существует.
Определение 39. Математическим ожиданием Eξ
случайной величины ξ с абсолютно непрерывным распределением с
плотностью распределения fξ(x), называется число , то говорят, что математическое ожидание не существует.
Определение 39. Математическим ожиданием Eξ
случайной величины ξ с абсолютно непрерывным распределением с
плотностью распределения fξ(x), называется число
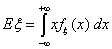 если указанный интеграл абсолютно сходится.
Если же если указанный интеграл абсолютно сходится.
Если же
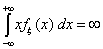 , то говорят, что математическое ожидание не существует.
Математическое ожидание имеет простой физический смысл: если на прямой
разместить единичную массу, поместив в точку аi массу p
i (для дискретного распределения), или «размазав» ее с плотностью
fξ(x) (для абсолютно непрерывного распределения), то точка E
ξ есть координата «центра тяжести» прямой.
Пример 26. Пусть случайная величина ξ равна числу очков,
выпадающих при одном подбрасывании кубика. Тогда , то говорят, что математическое ожидание не существует.
Математическое ожидание имеет простой физический смысл: если на прямой
разместить единичную массу, поместив в точку аi массу p
i (для дискретного распределения), или «размазав» ее с плотностью
fξ(x) (для абсолютно непрерывного распределения), то точка E
ξ есть координата «центра тяжести» прямой.
Пример 26. Пусть случайная величина ξ равна числу очков,
выпадающих при одном подбрасывании кубика. Тогда
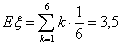
 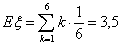 в среднем при подбрасывании кубика выпадает 3.5 очка
Пример 27. Пусть случайная величина ξ — координата точки,
брошенной наудачу на отрезок [a,b]. Тогда
в среднем при подбрасывании кубика выпадает 3.5 очка
Пример 27. Пусть случайная величина ξ — координата точки,
брошенной наудачу на отрезок [a,b]. Тогда
 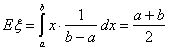 центр тяжести равномерного распределения на отрезке есть середина отрезка.
центр тяжести равномерного распределения на отрезке есть середина отрезка.
11.2 Свойства математического ожидания
Во всех свойствах предполагается, что рассматриваемые математические ожидания
существуют.
E0. Математическое ожидание случайной величины есть ЧИСЛО!
E1. Для произвольной функции функция g : R ® R
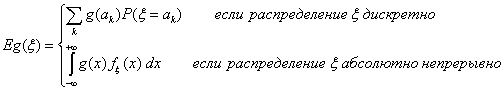 Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
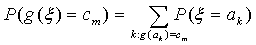 Тогда
Тогда
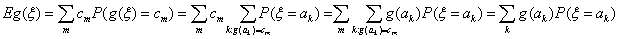 E2 Математическое ожидание const равно этой const Eс = с.
E3. const можно вынести за знак математического
ожидания: E(с ξ) = с Eξ.
Доказательство. Следует из свойства E1 при g(ξ) = с ξ .
E4. Математическое ожидание суммы любых случайных величин ξ и
η равно сумме их математических ожиданий.
E (ξ + η ) = E (ξ )+ E (η)
Доказательство. Для величин с дискретным распределением: пусть x
k и yn — значения ξ и η,
соответственно.
E2 Математическое ожидание const равно этой const Eс = с.
E3. const можно вынести за знак математического
ожидания: E(с ξ) = с Eξ.
Доказательство. Следует из свойства E1 при g(ξ) = с ξ .
E4. Математическое ожидание суммы любых случайных величин ξ и
η равно сумме их математических ожиданий.
E (ξ + η ) = E (ξ )+ E (η)
Доказательство. Для величин с дискретным распределением: пусть x
k и yn — значения ξ и η,
соответственно.
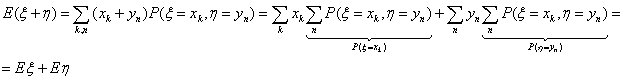 E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
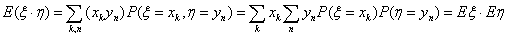 Замечание 16. Обратное утверждение к свойству E6 неверно: из
равенства E(ξη) = Eξ Eη. Не
следует независимость величин ξ и η.
Пример 28. Пусть φ Î U0,2π
, ξ = cos φ, η = sin φ— заведомо зависимые случайные
величины. Но математическое ожидание их произведения равно произведению их
математических ожиданий: по свойству E1
Замечание 16. Обратное утверждение к свойству E6 неверно: из
равенства E(ξη) = Eξ Eη. Не
следует независимость величин ξ и η.
Пример 28. Пусть φ Î U0,2π
, ξ = cos φ, η = sin φ— заведомо зависимые случайные
величины. Но математическое ожидание их произведения равно произведению их
математических ожиданий: по свойству E1
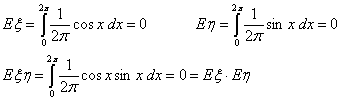
11.3 Моменты старших порядков. Дисперсия
Определение 40. Если 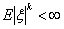 , то число , то число
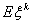 называется моментом порядка k (k -м моментом) случайной величины ξ; называется моментом порядка k (k -м моментом) случайной величины ξ;
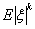 называется
абсолютным моментом порядка k (абсолютным k -м моментом) случайной
величины ξ; называется
абсолютным моментом порядка k (абсолютным k -м моментом) случайной
величины ξ;
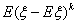 называется
центральным моментом порядка k (центральным k -м моментом) случайной
величины ξ; называется
центральным моментом порядка k (центральным k -м моментом) случайной
величины ξ;
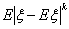 называется
абсолютным центральным моментом порядка k (абсолютным центральным k
-м моментом) случайной величины ξ.
Число Dξ = E(ξ – Eξ)2
(центральный момент порядка 2) называется дисперсией случайной величины
ξ
Пример 29. Пусть, скажем, случайная величина ξ принимает
значение 0 с вероятностью 1-10-5 , и значение 100 с вероятностью 10
-5. Посмотрим, как моменты разных порядков реагируют на большие, но
маловероятные значения случайной величины. называется
абсолютным центральным моментом порядка k (абсолютным центральным k
-м моментом) случайной величины ξ.
Число Dξ = E(ξ – Eξ)2
(центральный момент порядка 2) называется дисперсией случайной величины
ξ
Пример 29. Пусть, скажем, случайная величина ξ принимает
значение 0 с вероятностью 1-10-5 , и значение 100 с вероятностью 10
-5. Посмотрим, как моменты разных порядков реагируют на большие, но
маловероятные значения случайной величины.
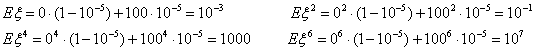 Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число
Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число 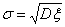 называют среднеквадратичным отклонением случайной величины ξ
.
Следует хорошо понимать, что из существования моментов больших порядков
следует существование моментов меньших порядков. В частности, конечность
второго момента (или дисперсии) влечет существование математического
ожидания.
называют среднеквадратичным отклонением случайной величины ξ
.
Следует хорошо понимать, что из существования моментов больших порядков
следует существование моментов меньших порядков. В частности, конечность
второго момента (или дисперсии) влечет существование математического
ожидания.
11.4 Свойства дисперсии
Все свойства дисперсии следуют из соответствующих свойств математического
ожидания.
D1. 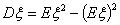 Действительно,
Действительно,
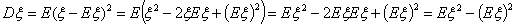 D2.
D2. 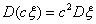 D3.
D3.
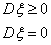 если и только если ξ= const.п.н.
Доказательство. Дисперсия есть всего-навсего математическое ожидание п.н.
неотрицательной с.в.:
Dξ = E(ξ – Eξ)2, и
неотрицательность дисперсии следует из свойства E5. По тому же свойству, D
ξ = 0 если и только если E(ξ – Eξ)2
= 0 п.н., то есть ξ = ξ п.н.
D4. Дисперсия не меняется от сдвига с.в. на постоянную: если и только если ξ= const.п.н.
Доказательство. Дисперсия есть всего-навсего математическое ожидание п.н.
неотрицательной с.в.:
Dξ = E(ξ – Eξ)2, и
неотрицательность дисперсии следует из свойства E5. По тому же свойству, D
ξ = 0 если и только если E(ξ – Eξ)2
= 0 п.н., то есть ξ = ξ п.н.
D4. Дисперсия не меняется от сдвига с.в. на постоянную:
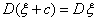 D5. Если ξ и η независимы, то
D5. Если ξ и η независимы, то
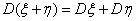 Действительно,
Действительно,
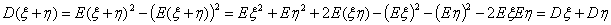 так как математическое ожидание произведения независимых с.в. равно
произведению их математических ожиданий.
D6. Минимум среднеквадратического отклонения случайной величины
ξ от точек вещественной прямой есть среднеквадратическое отклонение
ξ от своего математического ожидания:
так как математическое ожидание произведения независимых с.в. равно
произведению их математических ожиданий.
D6. Минимум среднеквадратического отклонения случайной величины
ξ от точек вещественной прямой есть среднеквадратическое отклонение
ξ от своего математического ожидания:
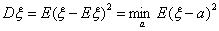 Наименьший момент инерции стержня с распределенной на нем единичной массой
получится, если точка вращения – центр тяжести стержня, а не любая другая
точка.
Доказательство.
Наименьший момент инерции стержня с распределенной на нем единичной массой
получится, если точка вращения – центр тяжести стержня, а не любая другая
точка.
Доказательство.
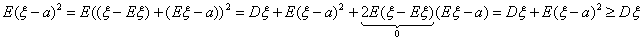 причем равенство достигается только для а = Eξ.
11.5 Математические ожидания и дисперсии стандартных распределений
Пример 31. Распределение Бернулли Вр,
причем равенство достигается только для а = Eξ.
11.5 Математические ожидания и дисперсии стандартных распределений
Пример 31. Распределение Бернулли Вр,
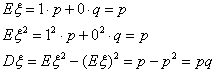 Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
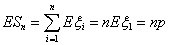 так как все ξi одинаково распределены и их
математическое ожидание равно pi;
так как все ξi одинаково распределены и их
математическое ожидание равно pi;
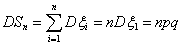 поскольку ξi независимы и дисперсия каждой равна pq.
Пример 33. Геометрическое распределение Gp
При p Î (0,1)
поскольку ξi независимы и дисперсия каждой равна pq.
Пример 33. Геометрическое распределение Gp
При p Î (0,1)
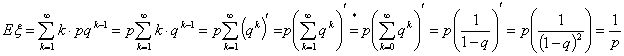 Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
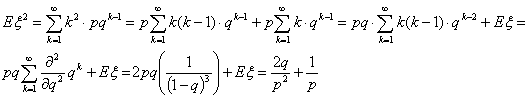 Поэтому
Пример 34. Распределение Пуассона Пλ
Поэтому
Пример 34. Распределение Пуассона Пλ

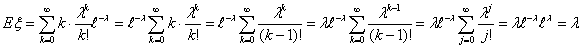 Показать, что
Показать, что
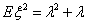 , следовательно , следовательно 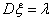 Пример 35. Равномерное распределение Ua,b
Пример 35. Равномерное распределение Ua,b
 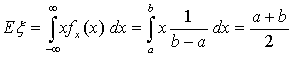
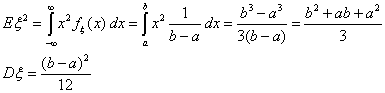 Пример 36. Стандартное нормальное распределение N0,1
Пример 36. Стандартное нормальное распределение N0,1
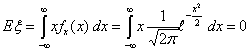 поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей
поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей 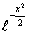 Последнее равенство следует из того, что
а интеграл по всей прямой от плотности любого распределения равен 1. Поэтому
Пример 37. Нормальное распределение
Последнее равенство следует из того, что
а интеграл по всей прямой от плотности любого распределения равен 1. Поэтому
Пример 37. Нормальное распределение 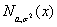 Мы знаем, что если
Мы знаем, что если
 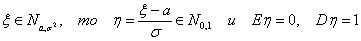 Поэтому
Поэтому
 Пример 38. Показательное (экспоненциальное) распределение Еα
Найдем для произвольного k Î N момент порядка k.
Пример 38. Показательное (экспоненциальное) распределение Еα
Найдем для произвольного k Î N момент порядка k.
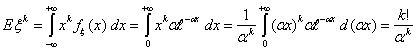 В последнем равенстве мы воспользовались гамма-функцией Эйлера:
В последнем равенстве мы воспользовались гамма-функцией Эйлера:
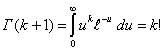 Соответственно, Соответственно,
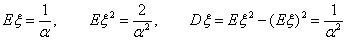 Пример 39. Стандартное распределение Коши С0,1
Распределение Коши. Говорят, что ξ имеет распределение Коши с
параметрами α, σ2, где α Î
R, σ > 0, если
Пример 39. Стандартное распределение Коши С0,1
Распределение Коши. Говорят, что ξ имеет распределение Коши с
параметрами α, σ2, где α Î
R, σ > 0, если
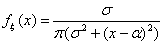 для всех х Î R
Распределение Коши имеет, например, абсцисса точки пересечения луча, посланного
из точки (α, σ) под наудачу выбранным углом, для всех х Î R
Распределение Коши имеет, например, абсцисса точки пересечения луча, посланного
из точки (α, σ) под наудачу выбранным углом,
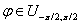 с осью ОХ.
Математическое ожидание для распределения Коши не существует, поскольку с осью ОХ.
Математическое ожидание для распределения Коши не существует, поскольку
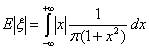 расходится (подинтегральная функция ведет себя на бесконечности как 1/х).
Пример 40. Распределение Парето
Распределение Парето. Говорят, что ξ имеет распределение Парето с
параметрами х0, s, где х0 > 0,
s > 0, если
расходится (подинтегральная функция ведет себя на бесконечности как 1/х).
Пример 40. Распределение Парето
Распределение Парето. Говорят, что ξ имеет распределение Парето с
параметрами х0, s, где х0 > 0,
s > 0, если
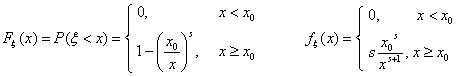 У распределения Парето существуют только моменты порядка u < s, поскольку
У распределения Парето существуют только моменты порядка u < s, поскольку
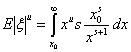 сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
Раздел 12. Числовые характеристики зависимости случайных величин
сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
Раздел 12. Числовые характеристики зависимости случайных величин
12.1 Чем отличается дисперсия суммы от суммы дисперсий?
Мы знаем, что для независимых с. в. с конечными вторыми моментами дисперсия
их суммы равна сумме их дисперсий. Чему равна дисперсия суммы в общем случае?
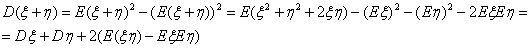 (10)
Величина E(ξη) - Eξ Eη равняется нулю,
если случайные величины ξ и η независимы (свойство
E6 математического ожидания). С другой стороны, из равенства ее нулю вовсе не
следует независимость, как показывает пример 30. Оказывается, что эту величину
часто используют как «индикатор наличия зависимости» пары с. в.
Определение 41. Ковариацией cov(ξ, η) случайных величин
ξ и η называется число
(10)
Величина E(ξη) - Eξ Eη равняется нулю,
если случайные величины ξ и η независимы (свойство
E6 математического ожидания). С другой стороны, из равенства ее нулю вовсе не
следует независимость, как показывает пример 30. Оказывается, что эту величину
часто используют как «индикатор наличия зависимости» пары с. в.
Определение 41. Ковариацией cov(ξ, η) случайных величин
ξ и η называется число
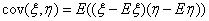 Свойство 10.
Свойство 10.
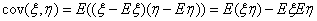 Свойство 11.
a)
Свойство 11.
a) 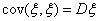 ;
b) ;
b) 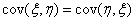 .
Свойство 12. Дисперсия суммы нескольких случайных величин вычисляется по
любой из следующих формул: .
Свойство 12. Дисперсия суммы нескольких случайных величин вычисляется по
любой из следующих формул:
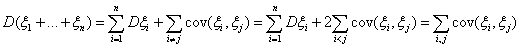 Обсудим достоинства и недостатки ковариации, как величины, характеризующей
зависимость двух с. в.
1. Если ковариация cov(ξ, η) отлична от нуля, то величины
ξ и η зависимы!
2. С гарантией о наличии зависимости мы можем судить, если знаем совместное
распределение пары ξ и η, и можем проверить, равна ли
(например) плотность совместного распределения произведению плотностей.
Но найти совместное распределение часто бывает сложнее, чем посчитать
математическое ожидание произведения ξ и η. Если нам
повезет, и математическое ожидание произведения ξ и η
не будет равняться произведению их мат. ожиданий, мы скажем, что ξ
и η зависимы не находя их совместного распределения!
Пример 41. Покажем, что с помощью ковариации можно судить о зависимости
даже когда для вычисления совместного распределения недостаточно данных.
Пусть ξ и η — независимые случайные величины,
и дисперсия ξ отлична от нуля. Докажем, что ξ и
ξ+ η зависимы.
Обсудим достоинства и недостатки ковариации, как величины, характеризующей
зависимость двух с. в.
1. Если ковариация cov(ξ, η) отлична от нуля, то величины
ξ и η зависимы!
2. С гарантией о наличии зависимости мы можем судить, если знаем совместное
распределение пары ξ и η, и можем проверить, равна ли
(например) плотность совместного распределения произведению плотностей.
Но найти совместное распределение часто бывает сложнее, чем посчитать
математическое ожидание произведения ξ и η. Если нам
повезет, и математическое ожидание произведения ξ и η
не будет равняться произведению их мат. ожиданий, мы скажем, что ξ
и η зависимы не находя их совместного распределения!
Пример 41. Покажем, что с помощью ковариации можно судить о зависимости
даже когда для вычисления совместного распределения недостаточно данных.
Пусть ξ и η — независимые случайные величины,
и дисперсия ξ отлична от нуля. Докажем, что ξ и
ξ+ η зависимы.
 (11)
Поэтому
(11)
Поэтому
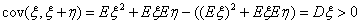 Следовательно, ξ и ξ+ η зависимы.
3. Жаль, что величина cov(ξ, η) не является «безразмерной»:
если ξ – объем газа в сосуде, а η – давление этого
газа, то ковариация измеряется в кубометрах х Паскали :).
Иначе говоря, при умножении одной из величин ξ, η на
какое-нибудь число ковариация тоже умножается на это число. Но умножение на
число не сказывается на «степени зависимости» величин (они от этого «более
зависимыми» не становятся), так что большое значение ковариации не означает
более сильной зависимости.
Нужно как-то нормировать ковариацию, получив из нее «безразмерную» величину,
абсолютное значение которой
а) не менялось бы при умножении или сдвиге случайных величин на число;
б) свидетельствовало бы о «силе зависимости» с. в.
Говря о «силе» зависимости между с.в., мы имеем в виду следующее. Самая
сильная зависимость – функциональная, а из функциональных – линейная
зависимость, когда ξ= аη + b п.н. Бывают гораздо более слабые
зависимости. Так, если по последовательности независимых случайных величин
ξ1 ξ2 . построить ξ = ξ1
+.ξ24 + ξ25 η = ξ
25 +ξ26 + .+ξ90 , то эти величины
зависимы, но очень “слабо зависимы”: через одно-единственное общее слагаемое
ξ25 .
Итак, следующая величина есть всего лишь ковариация, нормированная нужным
образом.
Следовательно, ξ и ξ+ η зависимы.
3. Жаль, что величина cov(ξ, η) не является «безразмерной»:
если ξ – объем газа в сосуде, а η – давление этого
газа, то ковариация измеряется в кубометрах х Паскали :).
Иначе говоря, при умножении одной из величин ξ, η на
какое-нибудь число ковариация тоже умножается на это число. Но умножение на
число не сказывается на «степени зависимости» величин (они от этого «более
зависимыми» не становятся), так что большое значение ковариации не означает
более сильной зависимости.
Нужно как-то нормировать ковариацию, получив из нее «безразмерную» величину,
абсолютное значение которой
а) не менялось бы при умножении или сдвиге случайных величин на число;
б) свидетельствовало бы о «силе зависимости» с. в.
Говря о «силе» зависимости между с.в., мы имеем в виду следующее. Самая
сильная зависимость – функциональная, а из функциональных – линейная
зависимость, когда ξ= аη + b п.н. Бывают гораздо более слабые
зависимости. Так, если по последовательности независимых случайных величин
ξ1 ξ2 . построить ξ = ξ1
+.ξ24 + ξ25 η = ξ
25 +ξ26 + .+ξ90 , то эти величины
зависимы, но очень “слабо зависимы”: через одно-единственное общее слагаемое
ξ25 .
Итак, следующая величина есть всего лишь ковариация, нормированная нужным
образом.
12.2 Коэффициент корреляции
Определение 43. Коэффициентом корреляции ρ(ξ, η)
случайных величин ξ, η, дисперсии которых существуют и отличны
от нуля, называется число
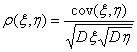 Пример 42. Рассмотрим продолжение примера 41, но пусть ξ
и η будут не только независимыми, но и одинаково распределенными
случайными величинами, и их дисперсия отлична от нуля. Найдем коэффициент
корреляции величин ξ и ξ + η. Согласно формуле (
10),
Пример 42. Рассмотрим продолжение примера 41, но пусть ξ
и η будут не только независимыми, но и одинаково распределенными
случайными величинами, и их дисперсия отлична от нуля. Найдем коэффициент
корреляции величин ξ и ξ + η. Согласно формуле (
10),
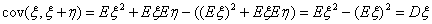 Поэтому
Поэтому
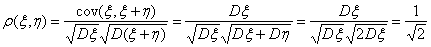 Определение 44. Случайные величины ξ и η
называют некоррелированными, если cov(ξ, η) = 0 (или
если ρ(ξ, η) = 0, — в том случае, когда коэффициент
корреляции существует).
Замечание 17. Если одна из величин ξ и η —
постоянная, то эти величины независимы, и cov (ξ, η) = 0.
Естественно в этом случае тоже полагать, что ξ и η
«некоррелированы», хотя коэффициент корреляции не определен (дисперсия
постоянной равна 0).
Определение 44. Случайные величины ξ и η
называют некоррелированными, если cov(ξ, η) = 0 (или
если ρ(ξ, η) = 0, — в том случае, когда коэффициент
корреляции существует).
Замечание 17. Если одна из величин ξ и η —
постоянная, то эти величины независимы, и cov (ξ, η) = 0.
Естественно в этом случае тоже полагать, что ξ и η
«некоррелированы», хотя коэффициент корреляции не определен (дисперсия
постоянной равна 0).
12.3 Свойства коэффициента корреляции
Всюду далее специально не оговаривается, но предполагается, что коэффициент
корреляции существует.
Теорема 26.
Коэффициент корреляции обладает следующими свойствами.
1. Если с. в. ξ и η независимы, то ρ(ξ,
η) = cov(ξ, η) = 0.
2. ½ρ(ξ, η)½£. 1
3. ½ρ(ξ, η)½= 1, если и только если
с. в. ξ и η с вероятностью 1 линейно связаны,
т.е. существуют числа а ¹ 0 и b такие, что P(η =
aξ+ b) = 1.
Определение 45. Пусть D конечна и отлична от нуля. Определим случайную величину
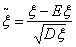 Преобразование
Преобразование  называется стандартизацией случайной величины ξ, а сама с.
в.
называется стандартизацией случайной величины ξ, а сама с.
в.  называется
стандартизованной , или (слэнг!) центрированной и нормированной
версией с. в. ξ.
Свойство 13. Стандартизованная с. в. называется
стандартизованной , или (слэнг!) центрированной и нормированной
версией с. в. ξ.
Свойство 13. Стандартизованная с. в.  имеет нулевое математическое ожидание и единичную дисперсию.
Доказательство. Воспользуемся свойствами математического ожидания и дисперсии:
имеет нулевое математическое ожидание и единичную дисперсию.
Доказательство. Воспользуемся свойствами математического ожидания и дисперсии:
 Полезно знать следующие часто употребляемые термины.
Определение 46. Говорят, что величины ξ и η
отрицательно коррелированы, если ρ(ξ, η) < 0;
говорят, что величины ξ и η положительно коррелированы
, если ρ(ξ, η) > 0.
Смысл знака коэффициента корреляции особенно ясен в случае ½
ρ(ξ, η) ½= 1. Тогда знак ρ равен
знаку a в равенстве η = aξ+ b п.н. То есть
ρ(ξ, η) = 1 означает, что чем больше ξ, тем
больше и η. Напротив, ρ(ξ, η) = -1
означает, что чем больше ξ, тем меньше η. Похожим
образом можно трактовать знак коэффициента корреляции и в случае, когда
½ρ(ξ, η) ½< 1, помня при этом, что
зависимость величин ξ и η теперь уже не линейная и,
возможно, даже не функциональная.
Так, величины ξ и ξ + η в примерах 41 и
42 положительно коррелированы, но их зависимость не функциональная.
Пример 43.
Полезно знать следующие часто употребляемые термины.
Определение 46. Говорят, что величины ξ и η
отрицательно коррелированы, если ρ(ξ, η) < 0;
говорят, что величины ξ и η положительно коррелированы
, если ρ(ξ, η) > 0.
Смысл знака коэффициента корреляции особенно ясен в случае ½
ρ(ξ, η) ½= 1. Тогда знак ρ равен
знаку a в равенстве η = aξ+ b п.н. То есть
ρ(ξ, η) = 1 означает, что чем больше ξ, тем
больше и η. Напротив, ρ(ξ, η) = -1
означает, что чем больше ξ, тем меньше η. Похожим
образом можно трактовать знак коэффициента корреляции и в случае, когда
½ρ(ξ, η) ½< 1, помня при этом, что
зависимость величин ξ и η теперь уже не линейная и,
возможно, даже не функциональная.
Так, величины ξ и ξ + η в примерах 41 и
42 положительно коррелированы, но их зависимость не функциональная.
Пример 43.
 Если с. в. ξ и η есть координаты точки, брошенной
наудачу в треугольник с вершинами (2,0), (0,0) и (0,1),
то коэффициент корреляции ρ(ξ, η) отрицателен. Это можно
объяснить «на пальцах» так: Чем больше ξ, тем меньше у η
возможностей быть большой) Предлагаю убедиться в этом, проверив
справедливость следующих высказываний.
Во-первых,
Если с. в. ξ и η есть координаты точки, брошенной
наудачу в треугольник с вершинами (2,0), (0,0) и (0,1),
то коэффициент корреляции ρ(ξ, η) отрицателен. Это можно
объяснить «на пальцах» так: Чем больше ξ, тем меньше у η
возможностей быть большой) Предлагаю убедиться в этом, проверив
справедливость следующих высказываний.
Во-первых,
 Во-вторых,
Совместное распределение координат точки, брошенной наудачу в произвольную
(измеримую) область D на плоскости имеет постоянную плотность во всех точках
области D. Это связано с понятием «наудачу»: вероятность попасть в любую
область AÌ D, с одной стороны зависит только от площади А и не зависит
от формы и положения А внутри D, равняясь с другой стороны, интегралу по
области А от плотности совместного распределения координат точки. Эти два
качества возможно совместить, только если плотность совместного распределения
постоянна внутри D. Более того, эта постоянная, как легко видеть, есть просто
Во-вторых,
Совместное распределение координат точки, брошенной наудачу в произвольную
(измеримую) область D на плоскости имеет постоянную плотность во всех точках
области D. Это связано с понятием «наудачу»: вероятность попасть в любую
область AÌ D, с одной стороны зависит только от площади А и не зависит
от формы и положения А внутри D, равняясь с другой стороны, интегралу по
области А от плотности совместного распределения координат точки. Эти два
качества возможно совместить, только если плотность совместного распределения
постоянна внутри D. Более того, эта постоянная, как легко видеть, есть просто 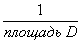 (хотя бы потому, что интеграл от нее по всей области D должен ровняться
вероятности попасть в D, или единице).
Распределение точки, брошенной наудачу в область (все равно где), называют
равномерным распределением.
Итак, плотность равномерного распределения в произвольной области на
плоскости — постоянная, равная (1/ площадь области) для точек внутри области
и нулю — вне. Поэтому (а также потому, что площадь этого треугольника равна
1)
(хотя бы потому, что интеграл от нее по всей области D должен ровняться
вероятности попасть в D, или единице).
Распределение точки, брошенной наудачу в область (все равно где), называют
равномерным распределением.
Итак, плотность равномерного распределения в произвольной области на
плоскости — постоянная, равная (1/ площадь области) для точек внутри области
и нулю — вне. Поэтому (а также потому, что площадь этого треугольника равна
1)
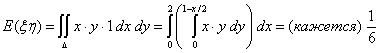 То есть ковариация (а с ней и коэффициент корреляции) отрицательна (посчитать
cov(ξ, η)).
Пример 44.
Найти коэффициент корреляции между числом выпадений единицы и числом выпадений
шестерки при n подбрасываниях симметричного кубика.
Решение. Обозначим для i = 1, 2, 3, 4, 5, 6 через ξ
i случайную величину, равную числу выпадений грани с i очками
при n подбрасываниях кубика. Посчитаем cov(ξ1,
ξ6).
Каждая из случайных величин ξi имеет биномиальное
распределение с параметрами n и 1/6, поэтому
То есть ковариация (а с ней и коэффициент корреляции) отрицательна (посчитать
cov(ξ, η)).
Пример 44.
Найти коэффициент корреляции между числом выпадений единицы и числом выпадений
шестерки при n подбрасываниях симметричного кубика.
Решение. Обозначим для i = 1, 2, 3, 4, 5, 6 через ξ
i случайную величину, равную числу выпадений грани с i очками
при n подбрасываниях кубика. Посчитаем cov(ξ1,
ξ6).
Каждая из случайных величин ξi имеет биномиальное
распределение с параметрами n и 1/6, поэтому
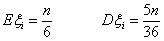 .
Заметим, что сумма ξ1 + . + ξn
этих величин равна n. В силу симметрии кубика, все математические
ожидания .
Заметим, что сумма ξ1 + . + ξn
этих величин равна n. В силу симметрии кубика, все математические
ожидания  одинаковы, но, скорее всего, отличаются от
одинаковы, но, скорее всего, отличаются от
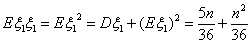 Посчитаем
Посчитаем
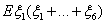 С одной стороны, это равно
С одной стороны, это равно
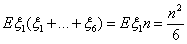 с другой стороны,
с другой стороны,
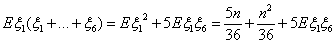 Отсюда
Отсюда
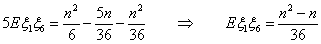 Следовательно, искомый коэффициент корреляции равен
Следовательно, искомый коэффициент корреляции равен
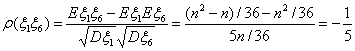 Интересно, что полученный коэффициент корреляции не зависит от n.
... Откуда, наконец, вытекает то удивительное, по-видимому, следствие, что,
если бы наблюдения над всеми событиями продолжать всю вечность, причем
вероятность, наконец, перешла бы в полную достоверность, то было бы замечено,
что в мире все управляется точными отношениями и постоянным законом изменений,
так что даже в вещах, в высшей степени случайных, мы принуждены были бы
признать как бы некоторую необходимость и, скажу я, рок.
Я к о б Б е р н у л л и, Ars conjectandi (1713)
Раздел 13. Куда и как сходятся последовательности случайных величин
Интересно, что полученный коэффициент корреляции не зависит от n.
... Откуда, наконец, вытекает то удивительное, по-видимому, следствие, что,
если бы наблюдения над всеми событиями продолжать всю вечность, причем
вероятность, наконец, перешла бы в полную достоверность, то было бы замечено,
что в мире все управляется точными отношениями и постоянным законом изменений,
так что даже в вещах, в высшей степени случайных, мы принуждены были бы
признать как бы некоторую необходимость и, скажу я, рок.
Я к о б Б е р н у л л и, Ars conjectandi (1713)
Раздел 13. Куда и как сходятся последовательности случайных величин
13.1 Сходимость «почти наверное» и «по вероятности»
Напомню, что случайная величина есть (измеримая) функция из некоторого
абстрактного множества Ω в множество действительных чисел.
Последовательность случайных величин есть, тем самым, последовательность
функций (определенных на одном и том же пространстве элементарных исходов
Ω). И если мы хотим говорить о сходимости последовательности случайных
величин {ξn }¥n=1
, не будем забывать, что мы имеем дело не с последовательностью чисел, а с
последовательностью функций. Существуют разные виды сходимости
последовательности функций. Всякий раз давать определение какой-либо сходимости
мы будем, опираясь на сходимость числовых последовательностей, как на
уже известное основное понятие.
В частности, при каждом новом ω Î Ω мы имеем новую
числовую последовательность {ξn (ω )}¥
n=1 . Поэтому, во-первых, можно говорить о знакомой из
математического анализа (почти) поточечной сходимости последовательностей
функций: о сходимости «почти всюду», которую в теории вероятностей называют
сходимостью «почти наверное».
Определение 46. Говорят, что последовательность с. в. {ξn
} сходится почти наверное к с. в. ξ при n ® ¥ , и
пишут: ξn ® ξ п. н., если P{ ω: ξ
n (ω ) ® ξ при n ® ¥} = 1.
Иначе говоря, если ξn (ω ) ® ξ при n ®
¥ для всех ω Î Ω, кроме, возможно, ω
Î A, где множество (событие) A имеет нулевую вероятность.
Заметим сразу: чтобы говорить о сходимости «почти наверное», требуется (по
крайней мере, по определению) знать, как устроены отображения ω ®
ξn (ω ). В задачах же теории вероятностей, как
правило, известны не сами случайные величины, а лишь их распределения.
Известно, то есть, какова вероятность тех элементарных исходов ω,
для которых ξn (ω ) принимает значения в заданном
множестве. Можем ли мы, обладая только информацией о распределениях, говорить о
какой-либо сходимости последовательности случайных величин {ξn
} к с. в. ξ?
Можно, например, потребовать, чтобы вероятность («доля») тех элементарных
исходов ω, для которых ξn (ω ) не
попадает в «ε-окрестность» числа ξ (ω ), уменьшалась до
нуля с ростом n. Такая сходимость в функциональном анализе называется
сходимостью «по мере», а в теории вероятностей — сходимостью «по вероятности».
Определение 47. Говорят, что последовательность с. в. { ξn
} сходятся по вероятности к с. в. ξ при n ® ¥, и
пишут:
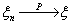 если для любого ε > 0
если для любого ε > 0
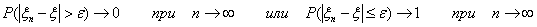 Пример 45. Рассмотрим последовательность с. в. ξ1
, ξ2, ., в которой все величины имеют разные
распределения: с. в. ξn, n > 0, принимает
значения и 0 и n7 с вероятностями
Пример 45. Рассмотрим последовательность с. в. ξ1
, ξ2, ., в которой все величины имеют разные
распределения: с. в. ξn, n > 0, принимает
значения и 0 и n7 с вероятностями 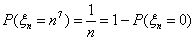 . Докажем, что эта последовательность сходится по вероятности к случайной
величине, равной нулю п. н. (к нулю, проще говоря).
Действительно, зафиксируем произвольное ε > 0. Для всех n
начиная с некоторого n0 такого, что n07
> ε верно равенство (*) ниже
. Докажем, что эта последовательность сходится по вероятности к случайной
величине, равной нулю п. н. (к нулю, проще говоря).
Действительно, зафиксируем произвольное ε > 0. Для всех n
начиная с некоторого n0 такого, что n07
> ε верно равенство (*) ниже
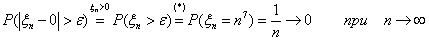 Итак, случайные величины ξn с ростом n могут
принимать все большие и большие значения, но со все меньшей и меньшей
вероятностью.
Замечание 18. Сходимость по вероятности не обязательно сопровождается
сходимостью математических ожиданий или моментов других порядков: из
Итак, случайные величины ξn с ростом n могут
принимать все большие и большие значения, но со все меньшей и меньшей
вероятностью.
Замечание 18. Сходимость по вероятности не обязательно сопровождается
сходимостью математических ожиданий или моментов других порядков: из  не следует, что
не следует, что  Действительно, в примере 45 имеет место сходимость
Действительно, в примере 45 имеет место сходимость 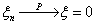 , но неверно, что , но неверно, что 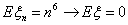 Если вместо значения n7 взять, скажем, n (с той же вероятностью 1/ n), получим
Если вместо значения n7 взять, скажем, n (с той же вероятностью 1/ n), получим
 А если ξn принимает значения 0 и
А если ξn принимает значения 0 и 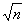 с теми же вероятностями, что и в примере 45, то
с теми же вероятностями, что и в примере 45, то 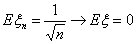 , но уже вторые моменты сходиться ко второму моменту ξ не будут:
, но уже вторые моменты сходиться ко второму моменту ξ не будут:
 Сходимость по вероятности обладает обычными для сходимостей свойствами.
Например, такими.
Свойство 13. Если
Сходимость по вероятности обладает обычными для сходимостей свойствами.
Например, такими.
Свойство 13. Если 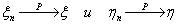 , то
1. , то
1. 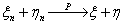 ;
2. ;
2.  .
Свойство 14.
Если .
Свойство 14.
Если  , и g – непрерывная функция, то , и g – непрерывная функция, то 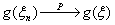 Если
Если 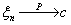 , и g – непрерывна в точке с, то , и g – непрерывна в точке с, то 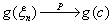 Чтобы доказывать сходимость по вероятности, можно просто уметь вычислять
Чтобы доказывать сходимость по вероятности, можно просто уметь вычислять 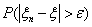 при больших n. Но для этого нужно знать распределение ξn
, что не всегда возможно. Скажем, ξn может быть суммой
нескольких других с. в., распределения которых не устойчивы по суммированию, и
вычислить распределение их суммы по формуле свертки или как-то еще бывает
слишком сложно.
Если бы мы имели неравенства, позволяющие оценить
при больших n. Но для этого нужно знать распределение ξn
, что не всегда возможно. Скажем, ξn может быть суммой
нескольких других с. в., распределения которых не устойчивы по суммированию, и
вычислить распределение их суммы по формуле свертки или как-то еще бывает
слишком сложно.
Если бы мы имели неравенства, позволяющие оценить 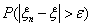 сверху чем-либо, что мы умеем устремлять к нулю и что проще вычисляется, то
сходимость по вероятности мы получили бы по лемме о двух милиционерах:
сверху чем-либо, что мы умеем устремлять к нулю и что проще вычисляется, то
сходимость по вероятности мы получили бы по лемме о двух милиционерах: 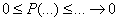 . Итак, неравенства П. Л. Чебышёва.
. Итак, неравенства П. Л. Чебышёва.
13.2 Неравенства Чебышёва
Все неравенства в этом параграфе принято относить к одному классу,
называемому «неравенствами Чебышёва». Следующее неравенство часто называют
собственно неравенством Чебышёва, хотя в такой форме оно появилось впервые,
видимо, в работах А. А. Маркова (например, Исчисление вероятностей, 1913 г.).
Теорема 27 (Неравенство Маркова).
Если 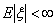 , то для любого положительного x , то для любого положительного x
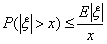 Доказательство. Введем новую случайную величину ξx
, называемую «срезкой» с. в. ½ξ½ на уровне x:
Доказательство. Введем новую случайную величину ξx
, называемую «срезкой» с. в. ½ξ½ на уровне x:
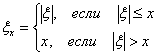 Для неё и,
1.
Для неё и,
1.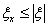 2.
2. 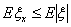 Нам потребуется следующее понятие.
Определение 48. Пусть A — некоторое событие. Назовем
индикатором события A случайную величину I(A), равную единице, если
событие A произошло, и нулю, если A не произошло.
По определению, I(A) имеет распределение Бернулли с параметром p =
P(I(A) = 1) = P(A), и ее математическое ожидание равно вероятности
успеха p = P(A).
Случайную величину ξх можно представить в виде
Нам потребуется следующее понятие.
Определение 48. Пусть A — некоторое событие. Назовем
индикатором события A случайную величину I(A), равную единице, если
событие A произошло, и нулю, если A не произошло.
По определению, I(A) имеет распределение Бернулли с параметром p =
P(I(A) = 1) = P(A), и ее математическое ожидание равно вероятности
успеха p = P(A).
Случайную величину ξх можно представить в виде
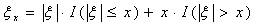 Тогда
Тогда
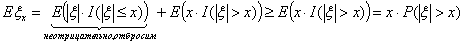 (11)
Вспомним, что
(11)
Вспомним, что 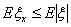 , и оценим , и оценим 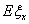 снизу согласно (11): снизу согласно (11):
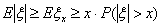 Итак,
Итак, 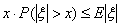 , что и требовалось доказать.
Следующее неравенство мы будем называть «обобщенным неравенством Чебышёва».
Следствие 12. Пусть функция g монотонно возрастает и
неотрицательна на [0,¥]. Если , что и требовалось доказать.
Следующее неравенство мы будем называть «обобщенным неравенством Чебышёва».
Следствие 12. Пусть функция g монотонно возрастает и
неотрицательна на [0,¥]. Если 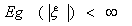 , то для любого положительного х
, то для любого положительного х
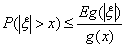 В 1853 г. И. Бьенеме (I. Bienayme) и в 1866 г., независимо от него, П. Л.
Чебышёв прямыми методами доказали следующее неравенство
Следствие 13 (Неравенство Чебышёва-Бьенеме). Если
В 1853 г. И. Бьенеме (I. Bienayme) и в 1866 г., независимо от него, П. Л.
Чебышёв прямыми методами доказали следующее неравенство
Следствие 13 (Неравенство Чебышёва-Бьенеме). Если 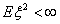 , то , то
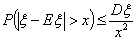 В качестве следствия получим так называемое «правило трех сигм», которое
формулируют, например, так: вероятность случайной величине отличаться от
своего математического ожидания более, чем на три корня из дисперсии, мала.
Разумеется, для каждого распределения величина этой вероятности своя: для
нормального распределения, например, эта вероятность равна 0,0027 — см.
свойство 9. Мы получим верную для всех распределений с конечной
дисперсией оценку сверху для «вероятности с. в. отличаться от своего
математического ожидания более, чем на три корня из дисперсии».
Следствие 14. Если
В качестве следствия получим так называемое «правило трех сигм», которое
формулируют, например, так: вероятность случайной величине отличаться от
своего математического ожидания более, чем на три корня из дисперсии, мала.
Разумеется, для каждого распределения величина этой вероятности своя: для
нормального распределения, например, эта вероятность равна 0,0027 — см.
свойство 9. Мы получим верную для всех распределений с конечной
дисперсией оценку сверху для «вероятности с. в. отличаться от своего
математического ожидания более, чем на три корня из дисперсии».
Следствие 14. Если 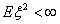 , то , то 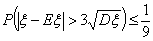
13.3 Законы больших чисел
Определение 49. Говорят, что последовательность с. в. 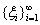 с конечными первыми моментами удовлетворяет закону больших чисел (ЗБЧ),
если
с конечными первыми моментами удовлетворяет закону больших чисел (ЗБЧ),
если
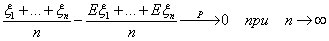 (12)
Законами больших чисел принято называть утверждения об условиях, при которых
последовательность с. в. «удовлетворяет закону больших чисел».
Выясним сначала, что означает и когда выполнен ЗБЧ для независимых и
одинаково распределенных с.в.
Заметим, что если с. в. одинакого распределены, то математические ожидания у них
одинаковы (и равны, например,
(12)
Законами больших чисел принято называть утверждения об условиях, при которых
последовательность с. в. «удовлетворяет закону больших чисел».
Выясним сначала, что означает и когда выполнен ЗБЧ для независимых и
одинаково распределенных с.в.
Заметим, что если с. в. одинакого распределены, то математические ожидания у них
одинаковы (и равны, например,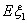 ), поэтому (12) можно записать в виде
), поэтому (12) можно записать в виде
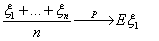 Итак, законы больших чисел.
Теорема 28 (ЗБЧ в форме Чебышёва).
Для любой последовательности независимых и одинаково распределенных
случайных величин с конечным вторым моментом
Итак, законы больших чисел.
Теорема 28 (ЗБЧ в форме Чебышёва).
Для любой последовательности независимых и одинаково распределенных
случайных величин с конечным вторым моментом 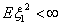 имеет место сходимость:
имеет место сходимость:
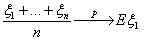 ЗБЧ утверждает, что среднее арифметическое большого числа случайных слагаемых
«стабилизируется» с ростом этого числа. Как бы сильно каждая с. в. не
отклонялась от своего среднего значения, при суммировании эти отклонения
«взаимно гасятся», так что среднее арифметическое приближается к постоянной
величине.
В дальнейшем мы увидим, что требование конечности второго момента (или
дисперсии) связано исключительно со способом доказательства, и что
утверждение остается верным если требовать существования только первого
момента.
Доказательство. Обозначим через
ЗБЧ утверждает, что среднее арифметическое большого числа случайных слагаемых
«стабилизируется» с ростом этого числа. Как бы сильно каждая с. в. не
отклонялась от своего среднего значения, при суммировании эти отклонения
«взаимно гасятся», так что среднее арифметическое приближается к постоянной
величине.
В дальнейшем мы увидим, что требование конечности второго момента (или
дисперсии) связано исключительно со способом доказательства, и что
утверждение остается верным если требовать существования только первого
момента.
Доказательство. Обозначим через 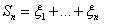 сумму первых n с. в., а их среднее арифметическое через
сумму первых n с. в., а их среднее арифметическое через 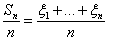 . Тогда
. Тогда
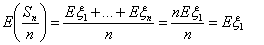 Пусть ε > 0. Воспользуемся неравенством Чебышёва (следствие 13):
Пусть ε > 0. Воспользуемся неравенством Чебышёва (следствие 13):
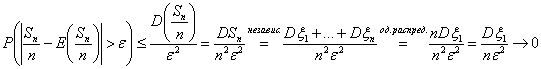 (13)
при
(13)
при 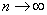 , поскольку , поскольку 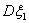 , по условию, конечна.
Следствие 15. Последовательность с. в. , по условию, конечна.
Следствие 15. Последовательность с. в. 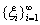 с конечными вторыми моментами удовлетворяет ЗБЧ, то есть
с конечными вторыми моментами удовлетворяет ЗБЧ, то есть
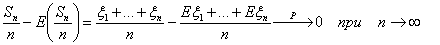 при выполнении любого из следующих условий:
а) если
при выполнении любого из следующих условий:
а) если 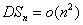 , то есть , то есть 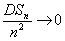 при при  ;
б) если ;
б) если 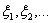 независимы и независимы и 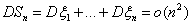 , то есть , то есть
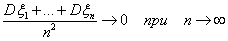 в) если
в) если 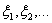 независимы,
одинаково распределены и имеют конечную дисперсию (ЗБЧ Чебышёва).
Теорема 29 (ЗБЧ в форме Хинчина).
Для любой последовательности независимых и одинаково распределенных случайных
величин с конечным первым моментом независимы,
одинаково распределены и имеют конечную дисперсию (ЗБЧ Чебышёва).
Теорема 29 (ЗБЧ в форме Хинчина).
Для любой последовательности независимых и одинаково распределенных случайных
величин с конечным первым моментом 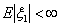 имеет место сходимость:
имеет место сходимость:
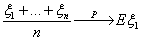 Более того, в условиях теоремы 29 имеет место сходимость «почти
наверное». Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Я.
Бернулли (1713). В отличие от доказанного через полтора столетия ЗБЧ Чебышёва,
описывающего предельное поведение среднего арифметического с. в. с
произвольными распределениями, ЗБЧ Бернулли — утверждение только для
схемы Бернулли.
Теорема 30 (ЗБЧ Бернулли).
Пусть А — событие, которое может произойти в любом из n
независимых испытаний с одной и той же вероятностью P(А). Пусть v
n(А) — число осуществлений события А в n испытаниях.
Тогда
Более того, в условиях теоремы 29 имеет место сходимость «почти
наверное». Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Я.
Бернулли (1713). В отличие от доказанного через полтора столетия ЗБЧ Чебышёва,
описывающего предельное поведение среднего арифметического с. в. с
произвольными распределениями, ЗБЧ Бернулли — утверждение только для
схемы Бернулли.
Теорема 30 (ЗБЧ Бернулли).
Пусть А — событие, которое может произойти в любом из n
независимых испытаний с одной и той же вероятностью P(А). Пусть v
n(А) — число осуществлений события А в n испытаниях.
Тогда
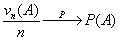 При этом для любого ε > 0
При этом для любого ε > 0
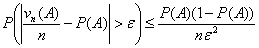
13.4 Примеры использования ЗБЧ и неравенства Чебышёва
Пример 46.
Монета подбрасывается 10 000 раз. Оценить вероятность того, что частота
выпадения герба отличается от вероятности более чем на одну сотую.
Требуется оценить 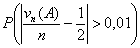 ,
где ,
где 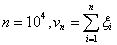 —число
выпадений герба, а —число
выпадений герба, а 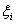 — независимые с. в., имеющие распределение Бернулли с параметром 1/2, равные
«числу гербов, выпавших при i-м подбрасывании» (то есть единице, если
выпал герб и нулю иначе, или индикатору того, что выпал герб). Поскольку
— независимые с. в., имеющие распределение Бернулли с параметром 1/2, равные
«числу гербов, выпавших при i-м подбрасывании» (то есть единице, если
выпал герб и нулю иначе, или индикатору того, что выпал герб). Поскольку 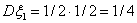 , искомая оценка сверху выглядит так:
, искомая оценка сверху выглядит так:
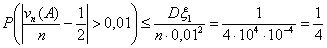 Иначе говоря, неравенство Чебышёва позволяет заключить, что, в среднем, не более
чем в четверти случаев при 10 000 подбрасываниях монеты частота выпадения герба
будет отличаться от 1/2 более чем на одну сотую. Мы увидим, насколько это
грубая оценка, когда познакомимся с центральной предельной теоремой.
Пример 47.
Пусть
Иначе говоря, неравенство Чебышёва позволяет заключить, что, в среднем, не более
чем в четверти случаев при 10 000 подбрасываниях монеты частота выпадения герба
будет отличаться от 1/2 более чем на одну сотую. Мы увидим, насколько это
грубая оценка, когда познакомимся с центральной предельной теоремой.
Пример 47.
Пусть 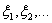 —
последовательность случайных величин, дисперсии которых ограничены одной и той
же постоянной С, а ковариации любых с. в. —
последовательность случайных величин, дисперсии которых ограничены одной и той
же постоянной С, а ковариации любых с. в. 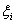 и
и 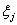 ( (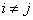 ), не являющихся соседними в последовательности, равны нулю. Удовлетворяет ли
эта последовательность ЗБЧ?
Воспользуемся неравенством (13) и свойством 12:
), не являющихся соседними в последовательности, равны нулю. Удовлетворяет ли
эта последовательность ЗБЧ?
Воспользуемся неравенством (13) и свойством 12:
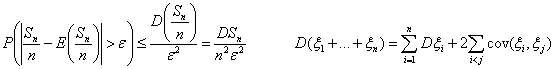 Но для i < j, по условию,
Но для i < j, по условию, 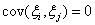 , если
, если 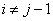 .
Следовательно, в сумме .
Следовательно, в сумме 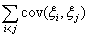 равны нулю все слагаемые кроме, может быть,
равны нулю все слагаемые кроме, может быть, 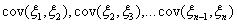 (их ровно n -1 штука).
Оценим каждое из них, используя одно из свойств коэффициента корреляции
(их ровно n -1 штука).
Оценим каждое из них, используя одно из свойств коэффициента корреляции
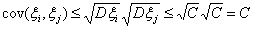 (по условию задачи) (по условию задачи)
 при
при  , т.е. последовательность , т.е. последовательность 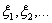 удовлетворяет ЗБЧ.
... Из этой первой лекции по теории вероятностей я запомнил только
полузнакомый термин «математическое ожидание». Незнакомец употреблял этот
термин неоднократно, и каждый раз я представлял себе большое помещение, вроде
зала ожидания, с кафельным полом, где сидят люди с портфелями и бюварами и,
подбрасывая время от времени к потолку монетки и бутерброды, сосредоточенно
чего-то ожидают. До сих пор я часто вижу это во сне. Но тут незнакомец оглушил
меня звонким термином «предельная теорема Муавра — Лапласа» и сказал, что все
это к делу не относится.
Аркадий и Борис Стругацкие, Стажеры удовлетворяет ЗБЧ.
... Из этой первой лекции по теории вероятностей я запомнил только
полузнакомый термин «математическое ожидание». Незнакомец употреблял этот
термин неоднократно, и каждый раз я представлял себе большое помещение, вроде
зала ожидания, с кафельным полом, где сидят люди с портфелями и бюварами и,
подбрасывая время от времени к потолку монетки и бутерброды, сосредоточенно
чего-то ожидают. До сих пор я часто вижу это во сне. Но тут незнакомец оглушил
меня звонким термином «предельная теорема Муавра — Лапласа» и сказал, что все
это к делу не относится.
Аркадий и Борис Стругацкие, Стажеры
Раздел 14. ЦПТ (центральная предельная теорема) 14.1 Как быстро 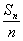 сходится к сходится к 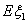 ? ?
Пусть, как в законе больших чисел в форме Чебышёва, 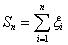 — сумма n независимых и одинаково распределенных величин с конечной
дисперсией. Тогда, в силу ЗБЧ,
— сумма n независимых и одинаково распределенных величин с конечной
дисперсией. Тогда, в силу ЗБЧ, 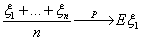 с ростом n. Или, после приведения к общему знаменателю,
с ростом n. Или, после приведения к общему знаменателю,
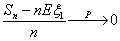 Если при делении на n мы получили в пределе нуль (в смысле некоторой,
все равно какой, сходимости), резонно задать себе вопрос: а не слишком ли на
«много» мы поделили? Нельзя ли поделить на что-нибудь, растущее к бесконечности
медленнее, чем n, чтобы получить в пределе не нуль (и не бесконечность,
само собой)?
Можно поставить этот вопрос по-другому. Вот последовательность, стремящаяся
(как-то) к нулю. Можно ли ее домножить на что-либо растущее, чтобы «погасить»
это стремление к нулю? Получив, тем самым, что-нибудь конечное и отличное от
нуля в пределе?
Оказывается, что уже
Если при делении на n мы получили в пределе нуль (в смысле некоторой,
все равно какой, сходимости), резонно задать себе вопрос: а не слишком ли на
«много» мы поделили? Нельзя ли поделить на что-нибудь, растущее к бесконечности
медленнее, чем n, чтобы получить в пределе не нуль (и не бесконечность,
само собой)?
Можно поставить этот вопрос по-другому. Вот последовательность, стремящаяся
(как-то) к нулю. Можно ли ее домножить на что-либо растущее, чтобы «погасить»
это стремление к нулю? Получив, тем самым, что-нибудь конечное и отличное от
нуля в пределе?
Оказывается, что уже 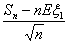 , или, что, то же самое,
, или, что, то же самое, 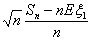 , не сходится к нулю. Распределение этой, зависящей от n, случайной
величины становится все более похоже на нормальное распределение! Можно
считать, что такая последовательность сходится к случайной величине, имеющей
нормальное распределение, но сходится не по вероятности, а только в смысле
сходимости распределений, или «слабой сходимости».
, не сходится к нулю. Распределение этой, зависящей от n, случайной
величины становится все более похоже на нормальное распределение! Можно
считать, что такая последовательность сходится к случайной величине, имеющей
нормальное распределение, но сходится не по вероятности, а только в смысле
сходимости распределений, или «слабой сходимости».
14.2 Слабая сходимость
Пусть задана последовательность с. в.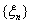 , задано некоторое распределение
, задано некоторое распределение 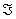 с функцией распределения
с функцией распределения 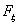 и
и 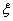 — произвольная с.
в., имеющая распределение — произвольная с.
в., имеющая распределение 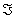 .
Определение 50. Говорят, что последовательность с. в.
.
Определение 50. Говорят, что последовательность с. в. 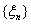 при
при 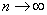 сходится
слабо или по распределению к с. в. сходится
слабо или по распределению к с. в. 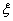 , или говорят, что последовательность с. в. слабо сходится к распределению
, или говорят, что последовательность с. в. слабо сходится к распределению 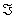 , или говорят, что распределения с.в.
, или говорят, что распределения с.в. 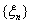 слабо сходится к распределению
слабо сходится к распределению 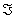 , и пишут:,
, и пишут:, 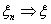 или или 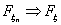 , или
, или 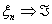 , если для
любого х такого, что функция распределения , если для
любого х такого, что функция распределения 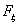 непрерывна в точке х, имеет место сходимость
непрерывна в точке х, имеет место сходимость 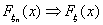 при
при 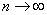 .
Иначе говоря, слабая сходимость — это поточечная сходимость функций
распределения во всех точках непрерывности предельной функции распределения.
Свойство 15. Если .
Иначе говоря, слабая сходимость — это поточечная сходимость функций
распределения во всех точках непрерывности предельной функции распределения.
Свойство 15. Если 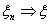 , и функция распределения
, и функция распределения 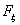 непрерывна в точках a и b, то
непрерывна в точках a и b, то 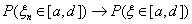 Наоборот, если во всех точках a и b непрерывности функции
распределения
Наоборот, если во всех точках a и b непрерывности функции
распределения 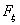 имеет место, например, сходимость
имеет место, например, сходимость 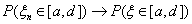 , то
, то 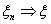 .
Следующее важное свойство уточняет отношения между сходимостями.
Свойство 16.
1. Если .
Следующее важное свойство уточняет отношения между сходимостями.
Свойство 16.
1. Если 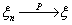 , то , то 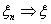 .
2. Если .
2. Если 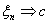 = const, то = const, то 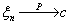 .
Доказательство.Докажем, что слабая сходимость к постоянной влечет
сходимость по вероятности.
Пусть .
Доказательство.Докажем, что слабая сходимость к постоянной влечет
сходимость по вероятности.
Пусть
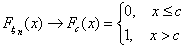 при любом x, являющемся точкой непрерывности предельной функции
при любом x, являющемся точкой непрерывности предельной функции 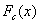 , то есть при всех
, то есть при всех 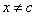 .
Возьмем произвольное .
Возьмем произвольное 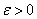 и докажем, что и докажем, что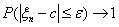 . Раскроем модуль: . Раскроем модуль:
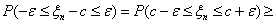 (сужаем событие под знаком вероятности)
(сужаем событие под знаком вероятности)
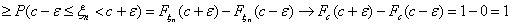 поскольку в точках
поскольку в точках 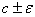 функция
функция  непрерывна,
и, следовательно, имеет место сходимость последовательности непрерывна,
и, следовательно, имеет место сходимость последовательности 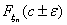 к
к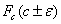 Осталось заметить, что
Осталось заметить, что 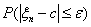 не бывает больше 1, так что по лемме о двух милиционерах
не бывает больше 1, так что по лемме о двух милиционерах 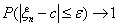 .
Следующее свойство приводит пример операций, которые можно применять к слабо
сходящимся последовательностям — скажем, домножать их на последовательности,
сходящиеся по вероятности к постоянным величинам.
Свойство 17.
1. Если
.
Следующее свойство приводит пример операций, которые можно применять к слабо
сходящимся последовательностям — скажем, домножать их на последовательности,
сходящиеся по вероятности к постоянным величинам.
Свойство 17.
1. Если 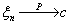 const и const и 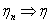 , то , то 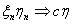 .
2. Если .
2. Если  const и const и 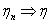 , то , то 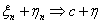 .
Несколько содержательных примеров слабой сходимости мы рассмотрим в следующей
главе. Но основной источник слабо сходящихся последовательностей и необычайно
мощное и универсальное средство для асимптотического анализа распределения
сумм независимых и одинаково распределенных случайных величин предоставляет
нам ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА .
Несколько содержательных примеров слабой сходимости мы рассмотрим в следующей
главе. Но основной источник слабо сходящихся последовательностей и необычайно
мощное и универсальное средство для асимптотического анализа распределения
сумм независимых и одинаково распределенных случайных величин предоставляет
нам ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
14.3 Центральная предельная теорема
Мы будем называть следующее утверждение «ЦПТ А. М. Ляпунова» (1901), но
сформулируем теорему Ляпунова только в частном случае — для
последовательности независимых и одинаково распределенных случайных величин.
Теорема 31 (ЦПТ).
Пусть 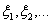 — независимые
и одинаково распределенные случайные величины с конечной и ненулевой
дисперсией: — независимые
и одинаково распределенные случайные величины с конечной и ненулевой
дисперсией: 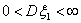 .
Обозначим через .
Обозначим через 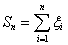 сумму первых n случайных величин. Тогда последовательность с. в.
сумму первых n случайных величин. Тогда последовательность с. в. 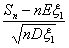 слабо сходится к стандартному нормальному распределению.
Пользуясь определением и свойствами слабой сходимости, и заметив, что функция
распределения
слабо сходится к стандартному нормальному распределению.
Пользуясь определением и свойствами слабой сходимости, и заметив, что функция
распределения  любого нормального закона непрерывна всюду на R, утверждение ЦПТ можно
сформулировать любым из следующих способов:
Следствие 18. Пусть
любого нормального закона непрерывна всюду на R, утверждение ЦПТ можно
сформулировать любым из следующих способов:
Следствие 18. Пусть  — независимые и одинаково распределенные случайные величины с конечной и
ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и
равносильны утверждению ЦПТ.
Для любых вещественных x < y при
— независимые и одинаково распределенные случайные величины с конечной и
ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и
равносильны утверждению ЦПТ.
Для любых вещественных x < y при 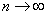 имеет место сходимость имеет место сходимость
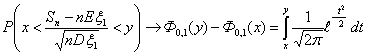 Для любых вещественных x < y при
Для любых вещественных x < y при  имеет место сходимость имеет место сходимость
 Для любых вещественных x < y при
Для любых вещественных x < y при 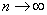 имеет место сходимость имеет место сходимость
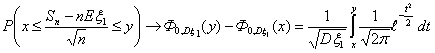 Если
Если 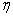 — произвольная с. в. со стандартным нормальным распределением, то — произвольная с. в. со стандартным нормальным распределением, то
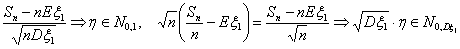 Замечание 19. Еще раз напомним, что функция распределения стандартного
нормального закона ищется либо по соответствующей таблице в справочнике, либо с
помощью какого-либо программного обеспечения, но никак не путем нахождения
первообразной.
Замечание 19. Еще раз напомним, что функция распределения стандартного
нормального закона ищется либо по соответствующей таблице в справочнике, либо с
помощью какого-либо программного обеспечения, но никак не путем нахождения
первообразной.
14.4 Предельная теорема Муавра — Лапласа
Получим в качестве следствия из ЦПТ предельную теорему Муавра — Лапласа (P. S.
Laplace, 1812; A. de Moivre, 1730). Подобно ЗБЧ Бернулли, предельная теорема
Муавра – Лапласа — утверждение только схемы Бернулли.
Теорема 32 (Предельная теорема Муавра — Лапласа).
Пусть А — событие, которое может произойти в любом из n
независимых испытаний с одной и той же вероятностью p = P(A). Пусть 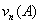 — число осуществлений события А в n испытаниях. Тогда
— число осуществлений события А в n испытаниях. Тогда 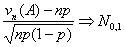 . Иначе говоря, для любых вещественных x < y при
. Иначе говоря, для любых вещественных x < y при  имеет место сходимость
имеет место сходимость
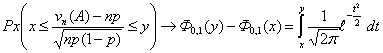
14.5 Примеры использования ЦПТ
Пример 48.
Монета подбрасывается 10 000 раз. Оценить вероятность того, что частота
выпадения герба отличается от вероятности более чем на одну сотую.
Требуется найти
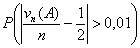 , где , где 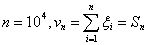 —число выпадений герба, а
—число выпадений герба, а 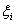 — независимые с. в., имеющие одно и то же распределение Бернулли с параметром
1/2. Домножим обе части неравенства под знаком вероятности на
— независимые с. в., имеющие одно и то же распределение Бернулли с параметром
1/2. Домножим обе части неравенства под знаком вероятности на 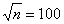 и поделим на корень из дисперсии
и поделим на корень из дисперсии 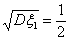 одного слагаемого.
одного слагаемого.
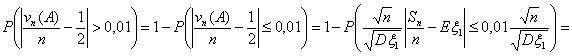
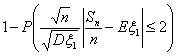 Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность
Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность
 слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную
с. в.
слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную
с. в. 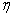 , имеющую
распределение , имеющую
распределение 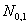 . .
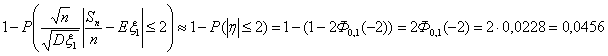 Равенство
Равенство 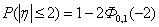 следует из свойства 10.
Замечание 20. Центральной предельной теоремой пользуются для
приближенного вычисления вероятностей, связанных с суммами большого числа
независимых и одинаково распределенных величин. При этом распределение
центрированной и нормированной суммы заменяют на стандартное нормальное
распределение.
Следующий результат позволяет оценить погрешность приближения в ЦПТ.
Теорема 33 (Неравенство Берри – Эссеена).
В условиях ЦПТ для любого х Î R (то есть равномерно по х) следует из свойства 10.
Замечание 20. Центральной предельной теоремой пользуются для
приближенного вычисления вероятностей, связанных с суммами большого числа
независимых и одинаково распределенных величин. При этом распределение
центрированной и нормированной суммы заменяют на стандартное нормальное
распределение.
Следующий результат позволяет оценить погрешность приближения в ЦПТ.
Теорема 33 (Неравенство Берри – Эссеена).
В условиях ЦПТ для любого х Î R (то есть равномерно по х)
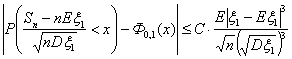 Замечание 21. Про постоянную С известно, что:
а) в общем случае С не превышает 0,7655 (И. С. Шиганов),
б) погрешность приближения наиболее велика, если слагаемые
Замечание 21. Про постоянную С известно, что:
а) в общем случае С не превышает 0,7655 (И. С. Шиганов),
б) погрешность приближения наиболее велика, если слагаемые 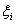 имеют распределение Бернулли, и С в этом случае не меньше, чем
имеют распределение Бернулли, и С в этом случае не меньше, чем  (C. G. Esseen, Б. А. Рогозин),
в) как показывают расчеты, можно смело брать в качестве С число 0,4 —
даже для слагаемых с распределением Бернулли, особенно при малых n,
когда и это значение постоянной оказывается слишком грубой оценкой.
Подробный обзор можно найти в монографии В.М.Золотарева «Современная теория
суммирования независимых случайных величин», стр. 264– 291.
Продолжение примера 48. Проверьте, что для с. в.
(C. G. Esseen, Б. А. Рогозин),
в) как показывают расчеты, можно смело брать в качестве С число 0,4 —
даже для слагаемых с распределением Бернулли, особенно при малых n,
когда и это значение постоянной оказывается слишком грубой оценкой.
Подробный обзор можно найти в монографии В.М.Золотарева «Современная теория
суммирования независимых случайных величин», стр. 264– 291.
Продолжение примера 48. Проверьте, что для с. в.  с распределением Бернулли с распределением Бернулли
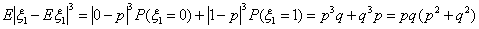 Поэтому разница между левой и правой частями приближенного равенства в примере
48 при
Поэтому разница между левой и правой частями приближенного равенства в примере
48 при 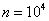 и и 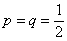 не превышает величины
не превышает величины
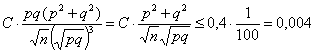 так что искомая вероятность
так что искомая вероятность 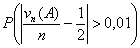 не больше, чем 0,0456+0,004. Уместно сравнить этот ответ с оценкой, полученной с
помощью ЗБЧ в примере 48.
Пример 49.
Пусть
не больше, чем 0,0456+0,004. Уместно сравнить этот ответ с оценкой, полученной с
помощью ЗБЧ в примере 48.
Пример 49.
Пусть 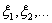 — независимые
и одинаково распределенные случайные величины с конечной и ненулевой
дисперсией, — независимые
и одинаково распределенные случайные величины с конечной и ненулевой
дисперсией, 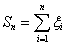 сумму
первых n случайных величин. При каких с имеет или не имеет
место сходимость сумму
первых n случайных величин. При каких с имеет или не имеет
место сходимость
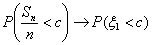 Согласно ЗБЧ, последовательность
Согласно ЗБЧ, последовательность 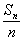 сходится по вероятности (а, следовательно, и слабо) к
сходится по вероятности (а, следовательно, и слабо) к 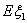 . Слабая сходимость означает, что последовательность функций распределения
. Слабая сходимость означает, что последовательность функций распределения 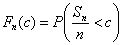 сходится к функции распределения
сходится к функции распределения 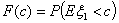 , если
, если 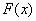 непрерывна в
точке с (и ничего не означает, если непрерывна в
точке с (и ничего не означает, если 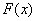 разрывна в точке с). Но
разрывна в точке с). Но
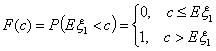 есть функция распределения вырожденного закона и непрерывна в любой точке с
, кроме
есть функция распределения вырожденного закона и непрерывна в любой точке с
, кроме  . Итак,
первый вывод: сходимость . Итак,
первый вывод: сходимость 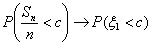 имеет место для любого с, кроме, возможно,
имеет место для любого с, кроме, возможно, 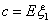 . Убедимся, что для
. Убедимся, что для 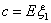 такой сходимости быть не может. Пусть
такой сходимости быть не может. Пусть 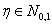 . Согласно ЦПТ,
. Согласно ЦПТ,
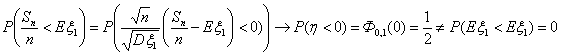 Аналогично, кстати, ведет себя и вероятность
Аналогично, кстати, ведет себя и вероятность 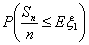 . Она тоже стремится к 1/2, а не к . Она тоже стремится к 1/2, а не к 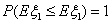
Страницы: 1, 2
|
|
|
|
|

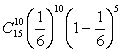 б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки,
выпадение единицы, выпадение остальных граней. Воспользоваться формулой для
числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.
Осталось изобрести формулу для подсчета вероятности каждому исходу в
нескольких независимых испытаниях выпасть нужное число раз, если в одном
испытании возможно не два, а более исходов.
Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, .m.
Пусть исход i в одном испытании случается с вероятностью рi, 1
≤ i ≤ m и
б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки,
выпадение единицы, выпадение остальных граней. Воспользоваться формулой для
числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.
Осталось изобрести формулу для подсчета вероятности каждому исходу в
нескольких независимых испытаниях выпасть нужное число раз, если в одном
испытании возможно не два, а более исходов.
Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, .m.
Пусть исход i в одном испытании случается с вероятностью рi, 1
≤ i ≤ m и
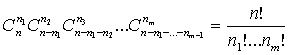 Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как
вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего
исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10
шестерок, 3 единицы и еще 2 других очка равна
Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как
вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего
исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10
шестерок, 3 единицы и еще 2 других очка равна
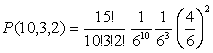
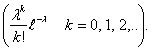 называется
распределением Пуассона с параметром λ.
Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее
десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с
вычисления которой мы начали. Поскольку n = 1000 «велико», а p
n = 0.003 «мало», то, взяв λ = n pn = 3 ,
можно написать приближенное равенство
называется
распределением Пуассона с параметром λ.
Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее
десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с
вычисления которой мы начали. Поскольку n = 1000 «велико», а p
n = 0.003 «мало», то, взяв λ = n pn = 3 ,
можно написать приближенное равенство
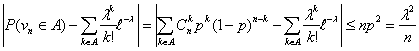 Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно
ли n «велико», а p «мало», руководствуясь полученной величиной
погрешности.
Какова же погрешность в формуле (6)?
Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно
ли n «велико», а p «мало», руководствуясь полученной величиной
погрешности.
Какова же погрешность в формуле (6)?
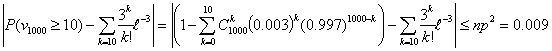 Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае,
можно утверждать, что искомая вероятность никак не больше, чем
0,01=0,001+0,009.
Рассмотрим еще одну формулу приближенного вычисления pn (m)
когда n велико. В отличии от предыдущего результата число успехов m в
этом случае тоже растет с ростом n, а вероятность успеха постоянна.
Локальная теорема Муавра – Лапласа
Пусть
Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае,
можно утверждать, что искомая вероятность никак не больше, чем
0,01=0,001+0,009.
Рассмотрим еще одну формулу приближенного вычисления pn (m)
когда n велико. В отличии от предыдущего результата число успехов m в
этом случае тоже растет с ростом n, а вероятность успеха постоянна.
Локальная теорема Муавра – Лапласа
Пусть 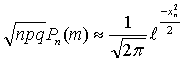 В частности, если
В частности, если 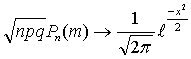 Доказательство:
В силу ограниченности величин
Доказательство:
В силу ограниченности величин 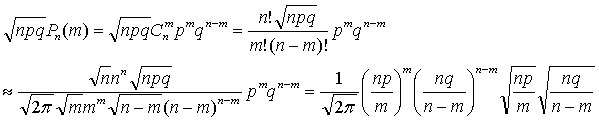 В силу определения
В силу определения 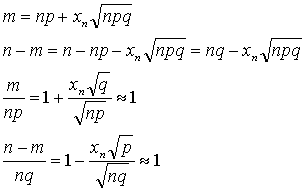


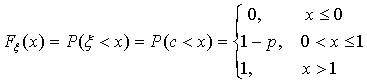 Пример 24. Будем говорить, что случайная величина ξ имеет
равномерное распределение на отрезке [a, b] и писать ξ
Î Ua,b (“ uniform”), если
ξ — координата точки, брошенной наудачу на отрезок [a, b]
числовой прямой. Это распределение можно задать и с помощью функции
распределения:
Пример 24. Будем говорить, что случайная величина ξ имеет
равномерное распределение на отрезке [a, b] и писать ξ
Î Ua,b (“ uniform”), если
ξ — координата точки, брошенной наудачу на отрезок [a, b]
числовой прямой. Это распределение можно задать и с помощью функции
распределения:

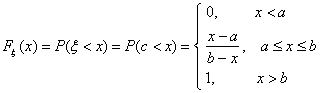
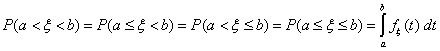 Доказательство. Действительно,
Доказательство. Действительно,
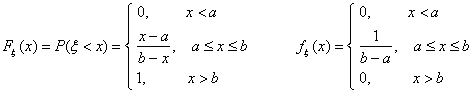 Заметьте, что в точках a и b функция распределения
недифференцируема, и плотность можно задать как угодно.
Показательное.
Говорят, что ξ имеет показательное распределение с параметром
α, α > 0 и ξ Î Еα
, если
Заметьте, что в точках a и b функция распределения
недифференцируема, и плотность можно задать как угодно.
Показательное.
Говорят, что ξ имеет показательное распределение с параметром
α, α > 0 и ξ Î Еα
, если
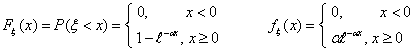 Показательное распределение является единственным абсолютно непрерывным
распределением, для которого выполнено свойство «не старения» (и в этом
смысле оно является непрерывным аналогом дискретного геометрического
распределения).
Теорема 21. Свойство «Не старения». Пусть ξ Î
Еα. Тогда для любых х, у > 0
Показательное распределение является единственным абсолютно непрерывным
распределением, для которого выполнено свойство «не старения» (и в этом
смысле оно является непрерывным аналогом дискретного геометрического
распределения).
Теорема 21. Свойство «Не старения». Пусть ξ Î
Еα. Тогда для любых х, у > 0
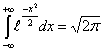 Нормальное (иначе называемое гауссовским по имени Карла Гаусса распределение
играет исключительно важную роль в теории вероятностей, поэтому мы очень
подробно изучим все свойства этого распределения.
Нормальное (иначе называемое гауссовским по имени Карла Гаусса распределение
играет исключительно важную роль в теории вероятностей, поэтому мы очень
подробно изучим все свойства этого распределения.
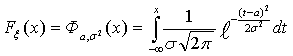
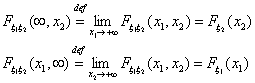 F3) Функция
F3) Функция 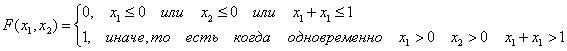 a) удовлетворяет всем свойствам (F0)-(F3);
б) не является функцией распределения никакого вектора (ξ1
, ξ2.) хотя бы потому, что, найдись такой вектор,
найдется и прямоугольник [a1 b1] x [a2
b2], вероятность попасть в который (вычисленная с помощью этой
«функции распределения») отрицательна:
P(a1 £ ξ1< b1 , a2 £ ξ2<b2 ) < 0!
Как же связана вероятность вектору попасть в прямоугольник с функцией
распределения этого вектора?
Упражнение. Доказать, что
P(a1 £ ξ1< b1 , a2
£ ξ2<b2 )= F ξ1
ξ2 (b1, b2) - F ξ
1 ξ2 (a1, b2) - F
ξ1 ξ2 (b1, a2
) + F ξ1 ξ2 (a1
, a2) (8)
Оказывается, если потребовать дополнительно от функции F, чтобы для всякого
[a1 b1] x [a2 b2]
вероятность P(a1 £ ξ1< b1]
, [a2 £ ξ2<b2], связанная
с функцией F равенством (8), была неотрицательна, то любая функция, обладающая
этим свойством и свойствами (F0)-(F3), уже будет функцией
распределения некоторого случайного вектора.
a) удовлетворяет всем свойствам (F0)-(F3);
б) не является функцией распределения никакого вектора (ξ1
, ξ2.) хотя бы потому, что, найдись такой вектор,
найдется и прямоугольник [a1 b1] x [a2
b2], вероятность попасть в который (вычисленная с помощью этой
«функции распределения») отрицательна:
P(a1 £ ξ1< b1 , a2 £ ξ2<b2 ) < 0!
Как же связана вероятность вектору попасть в прямоугольник с функцией
распределения этого вектора?
Упражнение. Доказать, что
P(a1 £ ξ1< b1 , a2
£ ξ2<b2 )= F ξ1
ξ2 (b1, b2) - F ξ
1 ξ2 (a1, b2) - F
ξ1 ξ2 (b1, a2
) + F ξ1 ξ2 (a1
, a2) (8)
Оказывается, если потребовать дополнительно от функции F, чтобы для всякого
[a1 b1] x [a2 b2]
вероятность P(a1 £ ξ1< b1]
, [a2 £ ξ2<b2], связанная
с функцией F равенством (8), была неотрицательна, то любая функция, обладающая
этим свойством и свойствами (F0)-(F3), уже будет функцией
распределения некоторого случайного вектора.
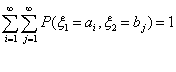 Таблицу, на пересечении i-й строки и j-го столбца которой (или
наоборот) стоит число
P(ξ1= ai ,ξ2=
bj) называют таблицей совместного распределения случайных
величин ξ1,. ξ2
Замечание 13. Напомню, что таблицы распределения каждой из случайных
величин ξ1, ξ2 в отдельности
(таблицы частных, или маргинальных распределений) восстанавливаются по
таблице совместного распределения с помощью очевидных формул:
Таблицу, на пересечении i-й строки и j-го столбца которой (или
наоборот) стоит число
P(ξ1= ai ,ξ2=
bj) называют таблицей совместного распределения случайных
величин ξ1,. ξ2
Замечание 13. Напомню, что таблицы распределения каждой из случайных
величин ξ1, ξ2 в отдельности
(таблицы частных, или маргинальных распределений) восстанавливаются по
таблице совместного распределения с помощью очевидных формул:
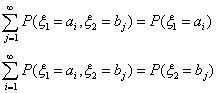 Если эти формулы вам не представляются очевидными, необходимо вернуться к
разделу 4 и перечитать определение 18 полной группы событий,
обратив также внимание на доказательство теоремы 8 (формулы полной
вероятности).
Если эти формулы вам не представляются очевидными, необходимо вернуться к
разделу 4 и перечитать определение 18 полной группы событий,
обратив также внимание на доказательство теоремы 8 (формулы полной
вероятности).
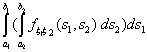 равняется объему под графиком функции f над областью интегрирования —
прямоугольником [a1,b1] x [a2,b
2].
Плотность совместного распределения обладает свойствами, аналогичными
свойствам плотности распределения одной случайной величины:
(f1)
равняется объему под графиком функции f над областью интегрирования —
прямоугольником [a1,b1] x [a2,b
2].
Плотность совместного распределения обладает свойствами, аналогичными
свойствам плотности распределения одной случайной величины:
(f1) 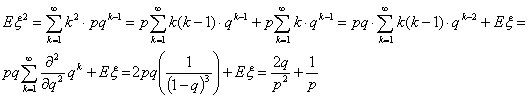 Поэтому
Пример 34. Распределение Пуассона Пλ
Поэтому
Пример 34. Распределение Пуассона Пλ
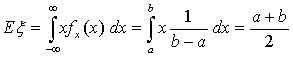
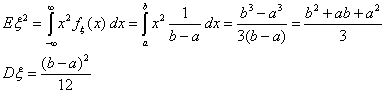 Пример 36. Стандартное нормальное распределение N0,1
Пример 36. Стандартное нормальное распределение N0,1
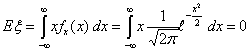 поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей
поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей 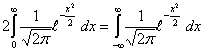
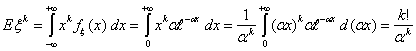 В последнем равенстве мы воспользовались гамма-функцией Эйлера:
В последнем равенстве мы воспользовались гамма-функцией Эйлера:
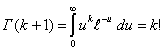 Соответственно,
Соответственно,
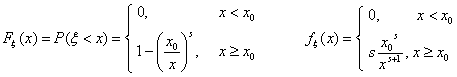 У распределения Парето существуют только моменты порядка u < s, поскольку
У распределения Парето существуют только моменты порядка u < s, поскольку
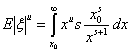 сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть
случайная величина мы всегда в праве от нее что-нибудь ожидать.»
Из студенческой контрольной работы.
сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
«Случайных величин без мат. ожидания не бывает, так как, если у нас есть
случайная величина мы всегда в праве от нее что-нибудь ожидать.»
Из студенческой контрольной работы.
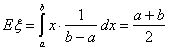 центр тяжести равномерного распределения на отрезке есть середина отрезка.
центр тяжести равномерного распределения на отрезке есть середина отрезка.
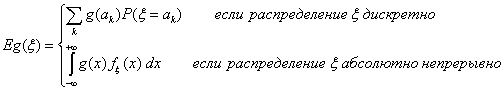 Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
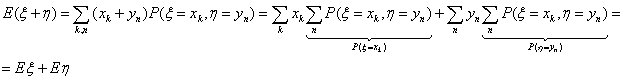 E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
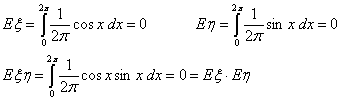
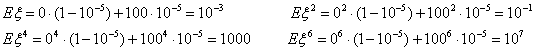 Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число
Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число 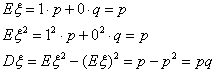 Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
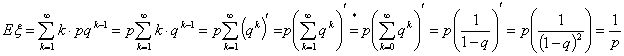 Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
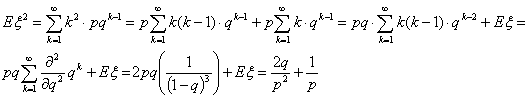 Поэтому
Пример 34. Распределение Пуассона Пλ
Поэтому
Пример 34. Распределение Пуассона Пλ
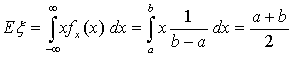
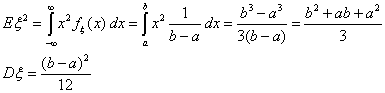 Пример 36. Стандартное нормальное распределение N0,1
Пример 36. Стандартное нормальное распределение N0,1
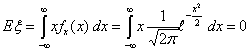 поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей
поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно
сходится (за счет быстро убывающей 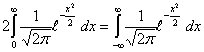
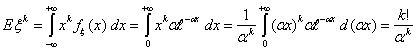 В последнем равенстве мы воспользовались гамма-функцией Эйлера:
В последнем равенстве мы воспользовались гамма-функцией Эйлера:
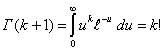 Соответственно,
Соответственно,
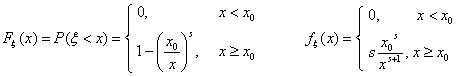 У распределения Парето существуют только моменты порядка u < s, поскольку
У распределения Парето существуют только моменты порядка u < s, поскольку
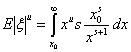 сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
Раздел 12. Числовые характеристики зависимости случайных величин
сходится при u < s, то есть когда подинтегральная функция на
бесконечности бесконечно мала по сравнению с 1/х.
Раздел 12. Числовые характеристики зависимости случайных величин 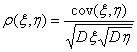 Пример 42. Рассмотрим продолжение примера 41, но пусть ξ
и η будут не только независимыми, но и одинаково распределенными
случайными величинами, и их дисперсия отлична от нуля. Найдем коэффициент
корреляции величин ξ и ξ + η. Согласно формуле (
10),
Пример 42. Рассмотрим продолжение примера 41, но пусть ξ
и η будут не только независимыми, но и одинаково распределенными
случайными величинами, и их дисперсия отлична от нуля. Найдем коэффициент
корреляции величин ξ и ξ + η. Согласно формуле (
10),
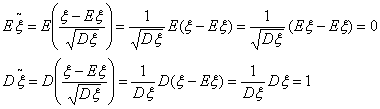 Полезно знать следующие часто употребляемые термины.
Определение 46. Говорят, что величины ξ и η
отрицательно коррелированы, если ρ(ξ, η) < 0;
говорят, что величины ξ и η положительно коррелированы
, если ρ(ξ, η) > 0.
Смысл знака коэффициента корреляции особенно ясен в случае ½
ρ(ξ, η) ½= 1. Тогда знак ρ равен
знаку a в равенстве η = aξ+ b п.н. То есть
ρ(ξ, η) = 1 означает, что чем больше ξ, тем
больше и η. Напротив, ρ(ξ, η) = -1
означает, что чем больше ξ, тем меньше η. Похожим
образом можно трактовать знак коэффициента корреляции и в случае, когда
½ρ(ξ, η) ½< 1, помня при этом, что
зависимость величин ξ и η теперь уже не линейная и,
возможно, даже не функциональная.
Так, величины ξ и ξ + η в примерах 41 и
42 положительно коррелированы, но их зависимость не функциональная.
Пример 43.
Полезно знать следующие часто употребляемые термины.
Определение 46. Говорят, что величины ξ и η
отрицательно коррелированы, если ρ(ξ, η) < 0;
говорят, что величины ξ и η положительно коррелированы
, если ρ(ξ, η) > 0.
Смысл знака коэффициента корреляции особенно ясен в случае ½
ρ(ξ, η) ½= 1. Тогда знак ρ равен
знаку a в равенстве η = aξ+ b п.н. То есть
ρ(ξ, η) = 1 означает, что чем больше ξ, тем
больше и η. Напротив, ρ(ξ, η) = -1
означает, что чем больше ξ, тем меньше η. Похожим
образом можно трактовать знак коэффициента корреляции и в случае, когда
½ρ(ξ, η) ½< 1, помня при этом, что
зависимость величин ξ и η теперь уже не линейная и,
возможно, даже не функциональная.
Так, величины ξ и ξ + η в примерах 41 и
42 положительно коррелированы, но их зависимость не функциональная.
Пример 43.
 Если с. в. ξ и η есть координаты точки, брошенной
наудачу в треугольник с вершинами (2,0), (0,0) и (0,1),
то коэффициент корреляции ρ(ξ, η) отрицателен. Это можно
объяснить «на пальцах» так: Чем больше ξ, тем меньше у η
возможностей быть большой) Предлагаю убедиться в этом, проверив
справедливость следующих высказываний.
Во-первых,
Если с. в. ξ и η есть координаты точки, брошенной
наудачу в треугольник с вершинами (2,0), (0,0) и (0,1),
то коэффициент корреляции ρ(ξ, η) отрицателен. Это можно
объяснить «на пальцах» так: Чем больше ξ, тем меньше у η
возможностей быть большой) Предлагаю убедиться в этом, проверив
справедливость следующих высказываний.
Во-первых,
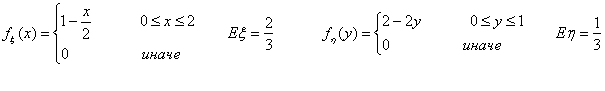 Во-вторых,
Совместное распределение координат точки, брошенной наудачу в произвольную
(измеримую) область D на плоскости имеет постоянную плотность во всех точках
области D. Это связано с понятием «наудачу»: вероятность попасть в любую
область AÌ D, с одной стороны зависит только от площади А и не зависит
от формы и положения А внутри D, равняясь с другой стороны, интегралу по
области А от плотности совместного распределения координат точки. Эти два
качества возможно совместить, только если плотность совместного распределения
постоянна внутри D. Более того, эта постоянная, как легко видеть, есть просто
Во-вторых,
Совместное распределение координат точки, брошенной наудачу в произвольную
(измеримую) область D на плоскости имеет постоянную плотность во всех точках
области D. Это связано с понятием «наудачу»: вероятность попасть в любую
область AÌ D, с одной стороны зависит только от площади А и не зависит
от формы и положения А внутри D, равняясь с другой стороны, интегралу по
области А от плотности совместного распределения координат точки. Эти два
качества возможно совместить, только если плотность совместного распределения
постоянна внутри D. Более того, эта постоянная, как легко видеть, есть просто 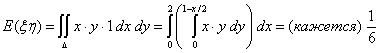 То есть ковариация (а с ней и коэффициент корреляции) отрицательна (посчитать
cov(ξ, η)).
Пример 44.
Найти коэффициент корреляции между числом выпадений единицы и числом выпадений
шестерки при n подбрасываниях симметричного кубика.
Решение. Обозначим для i = 1, 2, 3, 4, 5, 6 через ξ
i случайную величину, равную числу выпадений грани с i очками
при n подбрасываниях кубика. Посчитаем cov(ξ1,
ξ6).
Каждая из случайных величин ξi имеет биномиальное
распределение с параметрами n и 1/6, поэтому
То есть ковариация (а с ней и коэффициент корреляции) отрицательна (посчитать
cov(ξ, η)).
Пример 44.
Найти коэффициент корреляции между числом выпадений единицы и числом выпадений
шестерки при n подбрасываниях симметричного кубика.
Решение. Обозначим для i = 1, 2, 3, 4, 5, 6 через ξ
i случайную величину, равную числу выпадений грани с i очками
при n подбрасываниях кубика. Посчитаем cov(ξ1,
ξ6).
Каждая из случайных величин ξi имеет биномиальное
распределение с параметрами n и 1/6, поэтому
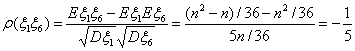 Интересно, что полученный коэффициент корреляции не зависит от n.
... Откуда, наконец, вытекает то удивительное, по-видимому, следствие, что,
если бы наблюдения над всеми событиями продолжать всю вечность, причем
вероятность, наконец, перешла бы в полную достоверность, то было бы замечено,
что в мире все управляется точными отношениями и постоянным законом изменений,
так что даже в вещах, в высшей степени случайных, мы принуждены были бы
признать как бы некоторую необходимость и, скажу я, рок.
Я к о б Б е р н у л л и, Ars conjectandi (1713)
Раздел 13. Куда и как сходятся последовательности случайных величин
Интересно, что полученный коэффициент корреляции не зависит от n.
... Откуда, наконец, вытекает то удивительное, по-видимому, следствие, что,
если бы наблюдения над всеми событиями продолжать всю вечность, причем
вероятность, наконец, перешла бы в полную достоверность, то было бы замечено,
что в мире все управляется точными отношениями и постоянным законом изменений,
так что даже в вещах, в высшей степени случайных, мы принуждены были бы
признать как бы некоторую необходимость и, скажу я, рок.
Я к о б Б е р н у л л и, Ars conjectandi (1713)
Раздел 13. Куда и как сходятся последовательности случайных величин 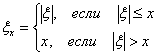 Для неё и,
1.
Для неё и,
1.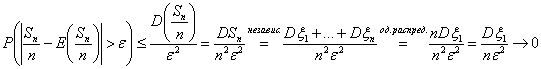 (13)
при
(13)
при 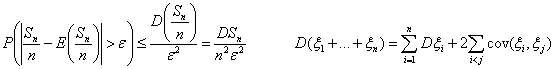 Но для i < j, по условию,
Но для i < j, по условию, 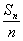 сходится к
сходится к 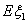 ?
?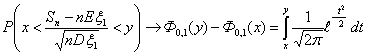 Для любых вещественных x < y при
Для любых вещественных x < y при 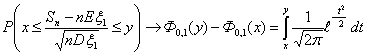 Для любых вещественных x < y при
Для любых вещественных x < y при 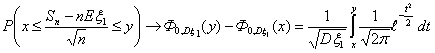 Если
Если 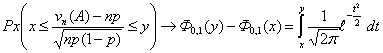
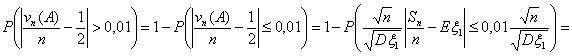
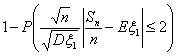 Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность
Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность
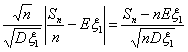 слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную
с. в.
слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную
с. в. 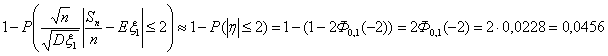 Равенство
Равенство 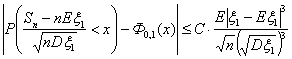 Замечание 21. Про постоянную С известно, что:
а) в общем случае С не превышает 0,7655 (И. С. Шиганов),
б) погрешность приближения наиболее велика, если слагаемые
Замечание 21. Про постоянную С известно, что:
а) в общем случае С не превышает 0,7655 (И. С. Шиганов),
б) погрешность приближения наиболее велика, если слагаемые 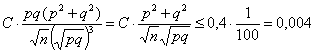 так что искомая вероятность
так что искомая вероятность 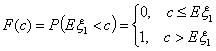 есть функция распределения вырожденного закона и непрерывна в любой точке с
, кроме
есть функция распределения вырожденного закона и непрерывна в любой точке с
, кроме 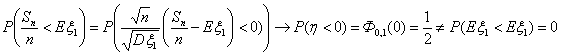 Аналогично, кстати, ведет себя и вероятность
Аналогично, кстати, ведет себя и вероятность 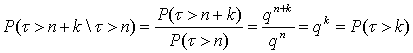
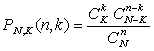
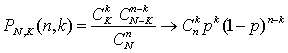
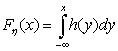 где
подинтегральная функция h(y) неотрицательна, то плотность распределения с.в.
η существует и в точности равна подинтегральной функции fξ
(x) = h(x) .
где
подинтегральная функция h(y) неотрицательна, то плотность распределения с.в.
η существует и в точности равна подинтегральной функции fξ
(x) = h(x) .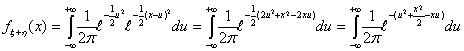 Выделим полный квадрат по u в показателе экспоненты:
Выделим полный квадрат по u в показателе экспоненты:
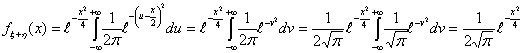 Последнее равенство верно поскольку под интегралом стоит плотность нормального
распределения с параметрами 0 и
Последнее равенство верно поскольку под интегралом стоит плотность нормального
распределения с параметрами 0 и 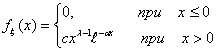 где постоянная c вычисляется из условия
где постоянная c вычисляется из условия
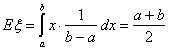 центр тяжести равномерного распределения на отрезке есть середина отрезка.
центр тяжести равномерного распределения на отрезке есть середина отрезка.
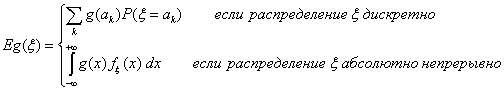 Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
Доказательство. Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения. Пусть g(ξ) принимает
значения с1 с2 . с вероятностями
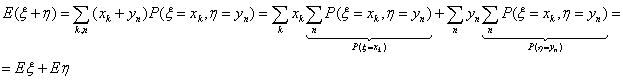 E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
E5.Если ξ ³ 0 п.н. (« почти наверное»,
т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ
³ 0;
Если ξ ³ 0 п.н., и при этом Eξ = 0
, то ξ = 0 п.н., то есть P(ξ = 0) = 1.
Следствие 11.
Если ξ £ η п.н., то E ξ £ Eη .
Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.
E6. Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.: если ξ
и η независимы, то
E(ξη) = Eξ Eη.
Доказательство.
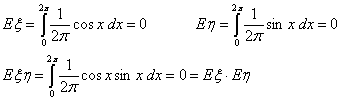
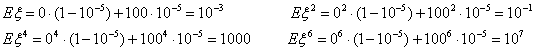 Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число
Пример 30. Дисперсия Dξ = E(ξ – Eξ)
2 есть «среднее значение квадрата отклонения случайной величины ξ
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть случайная величина ξ принимает значения +-1 с вероятностью
1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2.
Тогда Eξ = Eη = 0 поэтому D ξ = E
ξ2 = 1, Dη = Eη2 = 100.
Говорят, что дисперсия характеризует степень разброса значений случайной
величины вокруг ее математического ожидания.
Если говорить о распределении случайной величины, как о распределении
единичной массы по невесомому стержню, то дисперсия есть в точности момент
инерции этого стержня, закрепленного в центре тяжести.
Определение 40. Если дисперсия величины ξ конечна, то число 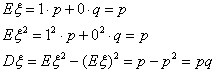 Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
Пример 32. Биномиальное распределение Вn,p
Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования — леммой 5. Возьмем n независимых случайных величин
ξ1 ξ2 . ξn, имеющих
распределение Бернулли В,p = В
1,p.
Тогда их сумма Sn = ξ1 + ξ2 +. + ξn имеет распределение Вn,p
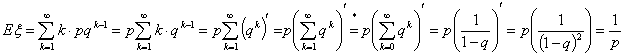 Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
Равенство (*) появилось из-за нежелания дифференцировать сумму
геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что
производная у добавленных слагаемых равна 0, так что производные от этих двух
сумм равны
