|
|
|
|
Лекция: Математическая Логика
Лекция: Математическая Логика
Конспекты лекций по математической логике.
1. Теория алгоритмов
1.1 Различные подходы к определению алгоритма:
10. Неформальное понятие алгоритма (последовательность инструкций
для выполнения действия).
20. Машина с неограниченными регистрами (МНР).
30 Машина Тьюринга – Поста (МТ-П).
40 Нормальные алгоритмы Маркова (НАМ).
1.1.1 Машина с неограниченными регистрами (МНР).
 Имеется некое устройство, в
котором счетное число ячеек памяти (регистров), в которых хранятся целые числа.
Допустимые команды:
Z(n) - обнуление регистра Rn.
S(n) - увеличение числа в регистре Rn на 1.
T(m,n) - копирует содержимое Rm в регистор Rn.
I(p,q,n) - если содержимое Rp = Rq то выполняется команда с номером n , если нет
следующая.
Программа для МНР должна быть последовательностью команд Z, S, T, I с
определенным порядком, выполняемые последовательно.
Тезис Черча (Churcha): Первое и второе определение
алгоритма эквивалентны между собой. Любой неформальный алгоритм может быть
представлен в программе для МНР. Имеется некое устройство, в
котором счетное число ячеек памяти (регистров), в которых хранятся целые числа.
Допустимые команды:
Z(n) - обнуление регистра Rn.
S(n) - увеличение числа в регистре Rn на 1.
T(m,n) - копирует содержимое Rm в регистор Rn.
I(p,q,n) - если содержимое Rp = Rq то выполняется команда с номером n , если нет
следующая.
Программа для МНР должна быть последовательностью команд Z, S, T, I с
определенным порядком, выполняемые последовательно.
Тезис Черча (Churcha): Первое и второе определение
алгоритма эквивалентны между собой. Любой неформальный алгоритм может быть
представлен в программе для МНР.
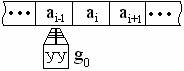 1.1.2 Машина Тьюринга - Поста.
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие
элементы алфавита: 1.1.2 Машина Тьюринга - Поста.
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие
элементы алфавита: 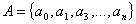 , где
, где 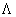 - пустой
символ (пустое слово), который может принадлежать и не принадлежать А.
Также существует управляющая головка (устройство) (УУ)/(УГ), которая в
начальный момент расположена в определенном месте, в состоянии - пустой
символ (пустое слово), который может принадлежать и не принадлежать А.
Также существует управляющая головка (устройство) (УУ)/(УГ), которая в
начальный момент расположена в определенном месте, в состоянии 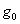 . Также существуют внутренние состояния машины:
. Также существуют внутренние состояния машины: 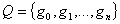 Слово в данном алфавите - любая конечная упорядоченная
последовательность букв данного алфавита, притом длина слова это количество
букв в нем (у пустого слова длина 0).
Допустимые команды:
Слово в данном алфавите - любая конечная упорядоченная
последовательность букв данного алфавита, притом длина слова это количество
букв в нем (у пустого слова длина 0).
Допустимые команды:
1) 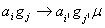 ,где ,где 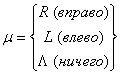 . . 2) 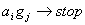 (остановка программы). (остановка программы). | Последовательность команд называется программой, если в этой последовательности не встречается команд с одинаковыми левыми частями. Машина останавливается если она не находит команды с левой частью подобной текущей. |
1.1.3 Нормальные алгоритмы Маркова.
Тип машины перерабатывающий слова, в которой существует некий алфавит 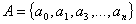 , для которого W - множество всех слов.
Допустимые команды: (Для машин этого типа важна последовательность команд.)
1.1.4 Реализация функции натурального переменного.
, для которого W - множество всех слов.
Допустимые команды: (Для машин этого типа важна последовательность команд.)
1.1.4 Реализация функции натурального переменного. 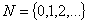
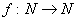 но мы допускаем не всюду определенную функцию. но мы допускаем не всюду определенную функцию.
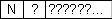  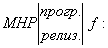 то это означает, что то это означает, что 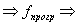 притом
притом 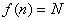 , если f не определена, то и программа не должна ничего выдавать. , если f не определена, то и программа не должна ничего выдавать.
  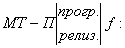 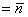 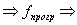 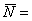 притом
притом 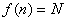 , если f не определена, то и программа не должна ничего выдавать.
( , если f не определена, то и программа не должна ничего выдавать.
(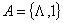 , а числа представляются в виде , а числа представляются в виде 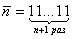 ,например ,например 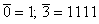 .)
1.2 Эквивалентность трех подходов к понятию алгоритм.
1.2.1 Теорема об эквивалентности понятия вычислимой функции. .)
1.2 Эквивалентность трех подходов к понятию алгоритм.
1.2.1 Теорема об эквивалентности понятия вычислимой функции.
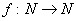 вычислима: ( вычислима: (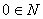 )
1) Если существует программа МНР, которая вычисляет эту функцию.
2) Если существует программа МТ-П, которая вычисляет эту функцию.
3) Если существует программа НАМ, которая вычисляет эту функцию.
Использование НАМ: )
1) Если существует программа МНР, которая вычисляет эту функцию.
2) Если существует программа МТ-П, которая вычисляет эту функцию.
3) Если существует программа НАМ, которая вычисляет эту функцию.
Использование НАМ: 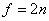 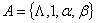
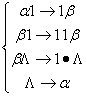 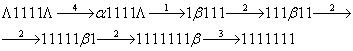
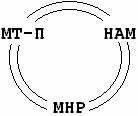 Теор.: Классы функций
вычислимых на МТ-П, с помощью НАМ и с помощью МНР совпадают.
Пусть Теор.: Классы функций
вычислимых на МТ-П, с помощью НАМ и с помощью МНР совпадают.
Пусть 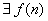 которая вычисляется на МТ-П, вычислим её на НАМ. которая вычисляется на МТ-П, вычислим её на НАМ.
МТ-П: 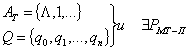
НАМ: 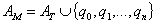 Команда МТП:
Команда МТП: 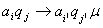 преобразуется по правилам: преобразуется по правилам:
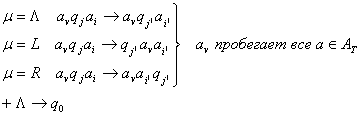 Команда МТП:
Команда МТП: 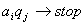 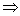 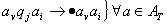 2. Булевы функции.
2.1 Основные определения
2.1.1 Декартово произведение
2. Булевы функции.
2.1 Основные определения
2.1.1 Декартово произведение
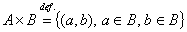 - мн-во всевозможных упорядоченных пар элементов из А и В.
Пример: - мн-во всевозможных упорядоченных пар элементов из А и В.
Пример: 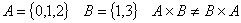
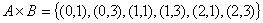 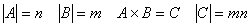
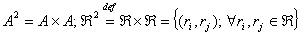 2.1.2 Декартова степень произвольного множества.
Опр:
2.1.2 Декартова степень произвольного множества.
Опр: 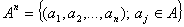 -
множество всевозможных упорядоченных наборов длины n , элементов множества А. -
множество всевозможных упорядоченных наборов длины n , элементов множества А. 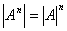 2.1.3 Определение булевой функции от n переменных.
Любое отображение
2.1.3 Определение булевой функции от n переменных.
Любое отображение 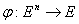 -
называется булевой функцией от n переменных, притом множество -
называется булевой функцией от n переменных, притом множество 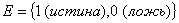
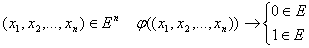 2.1.4 Примеры булевой функции.
1)
2.1.4 Примеры булевой функции.
1) 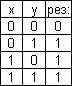 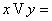 логическая сумма (дизъюнкция).
2) логическая сумма (дизъюнкция).
2) 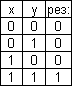 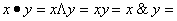 логическое умножение (конъюнкция).
3) логическое умножение (конъюнкция).
3) 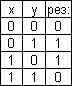 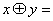 сложение по модулю два.
4) сложение по модулю два.
4) 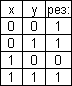 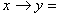 логическое следствие (импликация).
5) логическое следствие (импликация).
5) 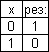 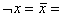 отрицание.
2.1.5 Основные булевы тождества.
1) отрицание.
2.1.5 Основные булевы тождества.
1) 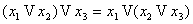 (ассоциативность)
2) (ассоциативность)
2) 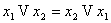 (коммутативность)
3) (коммутативность)
3) 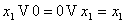 (свойство нуля)
4) (свойство нуля)
4) 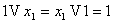 (закон поглощения для 1)
5) (закон поглощения для 1)
5) 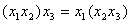 (ассоциативность)
6) (ассоциативность)
6) 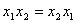 (коммутативность)
7) (коммутативность)
7) 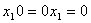 (свойство нуля по умножению)
8) (свойство нуля по умножению)
8) 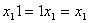 (свойство нейтральности 1 по умножению)
9) (свойство нейтральности 1 по умножению)
9) 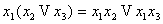 (дистрибутивность)
10) (дистрибутивность)
10) 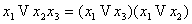 (дистрибутивность 2)
11) (дистрибутивность 2)
11) 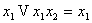 (закон поглощения)
12) (закон поглощения)
12) 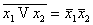 ( Законы
13) ( Законы
13) 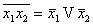 де Моргана)
14) де Моргана)
14) 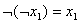 (закон снятия двойного отрицания)
15) (закон снятия двойного отрицания)
15) 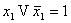 (tertium non datur – третьего не дано)
16) (tertium non datur – третьего не дано)
16) 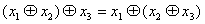 (ассоциативность)
17) (ассоциативность)
17) 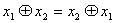 18)
18) 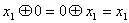 19)
19) 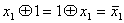 20)
20) 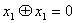 21)
21) 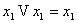 (Свойства
22) (Свойства
22) 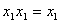 идемпотентности)
2.2 Дизъюнктивные нормальные формы.
2.2.1 Основные определения. идемпотентности)
2.2 Дизъюнктивные нормальные формы.
2.2.1 Основные определения.
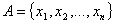 - конечный алфавит из переменных.
Рассмотрим слово: - конечный алфавит из переменных.
Рассмотрим слово: 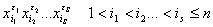 Экспоненциальные обозначения:
Экспоненциальные обозначения: 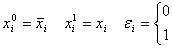
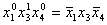 - элемент конъюнкции.
S – длина элемента конъюнкции.
ДНФ – дизъюнкция нескольких различных элементарных конъюнкций. - элемент конъюнкции.
S – длина элемента конъюнкции.
ДНФ – дизъюнкция нескольких различных элементарных конъюнкций.
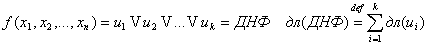 Любая булева функция может быть представлена как ДНФ
2.2.2 Теорема о совершенной ДНФ.
Любая булева функция
Любая булева функция может быть представлена как ДНФ
2.2.2 Теорема о совершенной ДНФ.
Любая булева функция 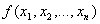 тождественно не равная 0 может быть разложена в ДНФ следующего вида:
тождественно не равная 0 может быть разложена в ДНФ следующего вида:
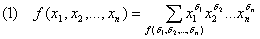 Опр: Носитель булевой функции
Опр: Носитель булевой функции 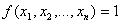
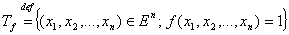 .
Лемма: .
Лемма: 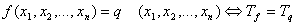 1)
1) 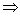 это элементарно это элементарно 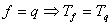 2)
2) 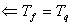 возьмем набор возьмем набор 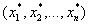 а)
а) 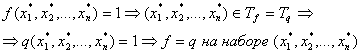 б)
б)
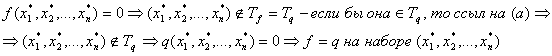 Доказательство:
Доказательство: 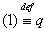 , будем доказывать, что , будем доказывать, что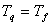 .
1) Докажем, что .
1) Докажем, что 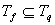 . Возьмем
. Возьмем 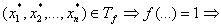 он
попадает в число суммируемых наборов и по нему будет проводиться сумирование. он
попадает в число суммируемых наборов и по нему будет проводиться сумирование.
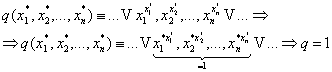 2) Докажем, что
2) Докажем, что 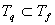 . Возьмем другой набор из . Возьмем другой набор из 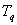
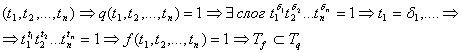 Следовательно
Следовательно 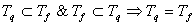 2.2.3 Некоторые другие виды ДНФ.
Опр:
2.2.3 Некоторые другие виды ДНФ.
Опр: 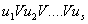 - называется
минимальной ДНФ, если она имеет - называется
минимальной ДНФ, если она имеет 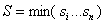 - наименьшую возможную длину из всех ДНФ данной функции.
Опр:
- наименьшую возможную длину из всех ДНФ данной функции.
Опр: 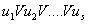 - называется
тупиковой ДНФ, если из неё нельзя выбросить ни одного слагаемого с
сохранением булевой функции.
(Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не
верно.)
Опр: К-мерной гранью называется такое подмножество - называется
тупиковой ДНФ, если из неё нельзя выбросить ни одного слагаемого с
сохранением булевой функции.
(Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не
верно.)
Опр: К-мерной гранью называется такое подмножество 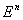 , которая является носителем некоторой элементарной конъюнкции длины: n-k.
Опр: Предположим дана функция
, которая является носителем некоторой элементарной конъюнкции длины: n-k.
Опр: Предположим дана функция 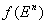 и есть
и есть 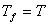 . Грань
называется отмеченной, если она целиком содержится в носителе
Т.
Опр: Максимальная грань – это такая грань, которая не содержится
ни в какой грани более высокой размерности.
Предложение: Любую отмеченную грань можно вложить в максимальную грань.
Предложение: . Грань
называется отмеченной, если она целиком содержится в носителе
Т.
Опр: Максимальная грань – это такая грань, которая не содержится
ни в какой грани более высокой размерности.
Предложение: Любую отмеченную грань можно вложить в максимальную грань.
Предложение:
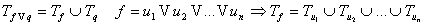 (Носитель любой функции можно разложить в объединение нескольких граней
разной размерностей)
Предложение: Носитель любой функции разлагается в объединение всех своих
максимальных граней.
(Носитель любой функции можно разложить в объединение нескольких граней
разной размерностей)
Предложение: Носитель любой функции разлагается в объединение всех своих
максимальных граней. 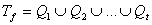 Опр: Элементарная конъюнкция называется минимальной, если её
носитель является максимальной гранью. Следовательно всякая булева функция
разлагается в дизъюнкцию всех своих элементарных конъюнкций.
Опр: Сокращенная ДНФ – разложение данной булевой функции в
соответствующие ДНФ, которые соответствуют объединению её максимальных граней.
Теор: Минимальная ДНФ может быть получена из сокращенной
отбрасыванием некоторого количества слагаемых, возможно пустого.
3 Логические Исчисления.
3.1 Исчисления высказывания (ИВ).
3.1.1 Определения.
Опр: Элементарная конъюнкция называется минимальной, если её
носитель является максимальной гранью. Следовательно всякая булева функция
разлагается в дизъюнкцию всех своих элементарных конъюнкций.
Опр: Сокращенная ДНФ – разложение данной булевой функции в
соответствующие ДНФ, которые соответствуют объединению её максимальных граней.
Теор: Минимальная ДНФ может быть получена из сокращенной
отбрасыванием некоторого количества слагаемых, возможно пустого.
3 Логические Исчисления.
3.1 Исчисления высказывания (ИВ).
3.1.1 Определения.
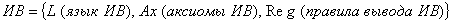
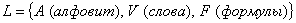
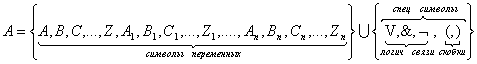 Опр: V – словом в алфавите А, называется любая конечная
упорядоченная последовательность его букв.
Опр: Формативная последовательность слов – конечная
последовательность слов и высказываний
Опр: V – словом в алфавите А, называется любая конечная
упорядоченная последовательность его букв.
Опр: Формативная последовательность слов – конечная
последовательность слов и высказываний 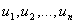 , если они имеют формат вида:
, если они имеют формат вида:
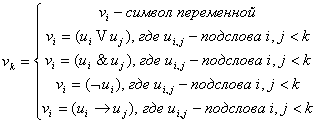 Опр: F – формулой ИВ, называется любое слово, входящее в
какую-нибудь формативную последовательность.
Пример:
Опр: F – формулой ИВ, называется любое слово, входящее в
какую-нибудь формативную последовательность.
Пример: 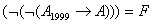
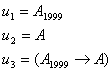 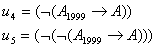 Опр: Аксиомы – специально выделенное подмножество формул.
Опр: Аксиомы – специально выделенное подмножество формул. 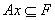 1)
1) 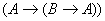 2)
2) 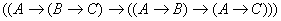 3)
3) 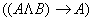 4)
4) 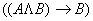 5)
5) 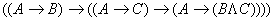 6)
6) 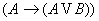 7)
7) 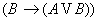 8)
8) 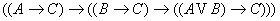 9)
9) 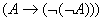 10)
10) 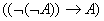 11)
11) 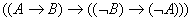 Reg – правила вывода ИВ (некоторые правила преобразования первого слова в
другое).
a – символ переменной
Reg – правила вывода ИВ (некоторые правила преобразования первого слова в
другое).
a – символ переменной 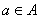
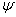 - произвольное слово ИВ (формула)
Отображение - произвольное слово ИВ (формула)
Отображение 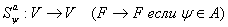 действует так, что на место каждого вхождения символа а , пишется слово
действует так, что на место каждого вхождения символа а , пишется слово 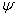 .
Пример:
.
Пример: 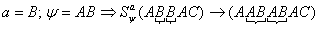 Правило modus ponens:
Правило modus ponens: 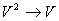 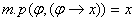 3.1.2 Формальный вывод.(простейшая модель доказательства теоремы)
Опр: Последовательность формул ИВ, называется формальным выводом, если каждая
формула этой последовательности имеет следующий вид:
3.1.2 Формальный вывод.(простейшая модель доказательства теоремы)
Опр: Последовательность формул ИВ, называется формальным выводом, если каждая
формула этой последовательности имеет следующий вид:
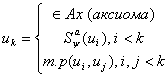 Опр: Выводимый формулой (теоремой) ИВ называется любая формула входящая в
какой-нибудь формальный вывод.
Опр: Выводимый формулой (теоремой) ИВ называется любая формула входящая в
какой-нибудь формальный вывод. 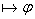 - выводимая формула ИВ.
Пример:
- выводимая формула ИВ.
Пример: 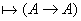 Правило одновременной подстановки.
Замечание: Если формула
Правило одновременной подстановки.
Замечание: Если формула 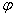 выводима, то выводима и выводима, то выводима и 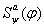 Возьмем формативную последовательность вывода
Возьмем формативную последовательность вывода 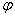 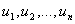 и добавим в неё
и добавим в неё 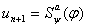 ,
получившаяся последовательность является формальным выводом.
(Если выводима ,
получившаяся последовательность является формальным выводом.
(Если выводима 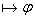 то если то если 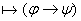 , то выводима , то выводима 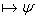 )
Теор: Если выводимая формула )
Теор: Если выводимая формула 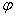 , то , то 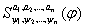 ( (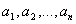 - различные символы переменных) выводима
Выберем - различные символы переменных) выводима
Выберем 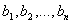 - символы
переменных которые различны между собой и не входят не в одну из формул - символы
переменных которые различны между собой и не входят не в одну из формул 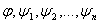 , сделаем подстановку
, сделаем подстановку 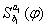 и последовательно применим
и последовательно применим 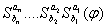 и в новом слове делаем последовательную подстановку:
и в новом слове делаем последовательную подстановку: 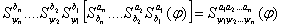 , где
, где 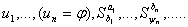 - является
формальным выводом.
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез - является
формальным выводом.
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез 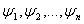 (формулы), называется такая последовательность слов
(формулы), называется такая последовательность слов 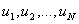 , каждая из которых удовлетворяет условию:
, каждая из которых удовлетворяет условию:
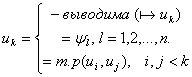
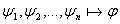 если формулу если формулу 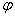 можно включить в некоторый формальный вывод из гипотез можно включить в некоторый формальный вывод из гипотез 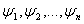 .
Лемма: .
Лемма: 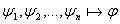 ; ; 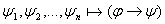 : то тогда : то тогда 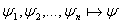 Напишем список:
Напишем список:
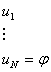 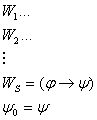 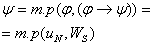 Лемма:
Лемма:
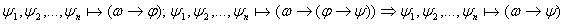 Док:
Док: 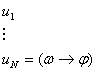 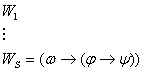 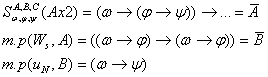 3.1.4 Теорема Дедукции.
Если из
3.1.4 Теорема Дедукции.
Если из
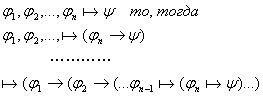 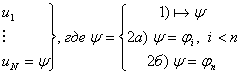 1) и 2а)
1) и 2а) 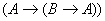 , где , где 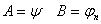 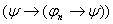 по правилу m.p. по правилу m.p. 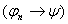 , ч.т.д.
2б) , ч.т.д.
2б) 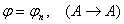 - уже выводили - уже выводили 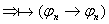 , ч.т.д.
Базис индукции: N=1 , ч.т.д.
Базис индукции: N=1 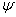 - формальный вывод из длинного списка - формальный вывод из длинного списка 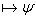
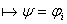 (только что доказано), осуществим переход по индукции: (только что доказано), осуществим переход по индукции:
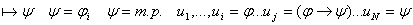
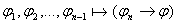 по индукции по индукции
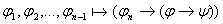 и по лемме 2 и по лемме 2
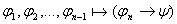 Пример:
Пример: 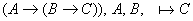
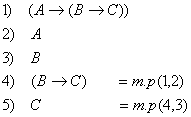 по теореме дедукции по теореме дедукции 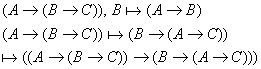 3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
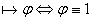 - тавтология
при любой интерпретации алфавита (символов переменных) - тавтология
при любой интерпретации алфавита (символов переменных)
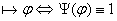 3.2.2 Понятие интерпретации.
3.2.2 Понятие интерпретации.
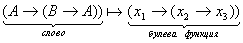 символ переменной
символ переменной 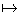 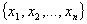 переменную поставим в соответствие. переменную поставим в соответствие.
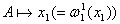 , где , где 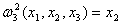 - проекция на - проекция на 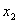 . .
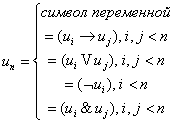 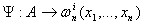
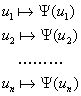 ; ; 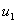 - только символ
переменных, т.к.
это заглавное слово
формативной последо-
вательности вида:
Где: - только символ
переменных, т.к.
это заглавное слово
формативной последо-
вательности вида:
Где:
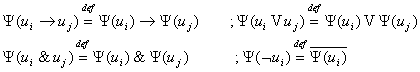 3.2.3 Доказательство теоремы.
3.2.3 Доказательство теоремы.
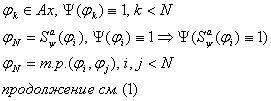 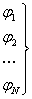
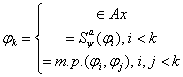 формальный
вывод формальный
вывод 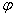
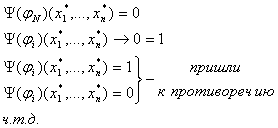 (1)
(1) 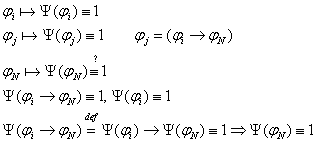 3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем.
3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем. 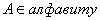 .
2) .
2) 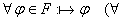 формула выводима в ИВ) формула выводима в ИВ)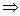 ИВ противоречиво.
3) ИВ противоречиво.
3) 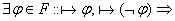 ИВ противоречиво.
ИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к
любому из трех определений.
Док-во: (1) Если ИВ противоречиво.
ИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к
любому из трех определений.
Док-во: (1) Если 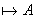 , то соответствующая ей булева функция будет тождественно равна 1.
, то соответствующая ей булева функция будет тождественно равна 1.
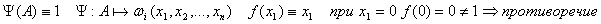 (2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.
(3) Пусть
(2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.
(3) Пусть 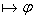 и и 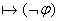 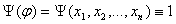 - булева функция - булева функция
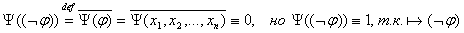 - противоречие.
3.4 Формальные исчисления.
Алфавит – конечное или счетное множество символов, возможно,
разбитых на группы. Алфавит должен быть упорядоченным множеством.
Слово – конечная упорядоченная последовательность символов
алфавита, в т.ч. пустое слово.
V – множество всех слов.
Вычислимая функция от нескольких натуральных переменных
- противоречие.
3.4 Формальные исчисления.
Алфавит – конечное или счетное множество символов, возможно,
разбитых на группы. Алфавит должен быть упорядоченным множеством.
Слово – конечная упорядоченная последовательность символов
алфавита, в т.ч. пустое слово.
V – множество всех слов.
Вычислимая функция от нескольких натуральных переменных 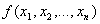 ( f – может быть не всюду определенной )
f – называется вычислимой, если
( f – может быть не всюду определенной )
f – называется вычислимой, если 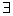 такая машина Тьюринга, которая её вычисляет. такая машина Тьюринга, которая её вычисляет.
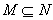 - разрешимое множество, если характеристическая функция - разрешимое множество, если характеристическая функция
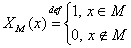 - является вычислимой.
Множество - является вычислимой.
Множество 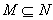 называется перечислимым, если называется перечислимым, если 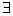 такая вычислимая функция такая вычислимая функция
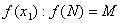 М - разрешимо
М - разрешимо 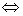 М и N \M перечислимы.
М – перечислимо М и N \M перечислимы.
М – перечислимо 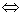 М – область определения некоторой вычислимой функции.
Множество всех формул F – некоторое разрешимое подмножество V.
Т – счетное множество, если М – область определения некоторой вычислимой функции.
Множество всех формул F – некоторое разрешимое подмножество V.
Т – счетное множество, если 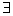 его биективное отображение на V. его биективное отображение на V.
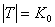 - обозначение счетного множества. ( - обозначение счетного множества. (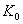 - алеф-нуль)
Если - алеф-нуль)
Если 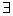 и зафиксировано биективное и вычислимое отображение и зафиксировано биективное и вычислимое отображение 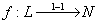 (вычис.),
то L – ансамбль.
V – ансамбль (слова лексикографически упорядочены и занумерованы)
Определение: В произвольном формальном исчислении: (вычис.),
то L – ансамбль.
V – ансамбль (слова лексикографически упорядочены и занумерованы)
Определение: В произвольном формальном исчислении: 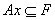 - множество всех аксиом – разрешимое подмножество множества всех формул.
- множество всех аксиом – разрешимое подмножество множества всех формул.
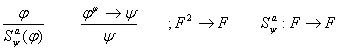 Правило вывода:
Правило вывода:
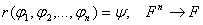 ,при ,при 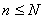 разрешимо. Для ИВ N=2.
Пример: разрешимо. Для ИВ N=2.
Пример:
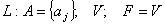 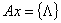 (пустое слово) , (пустое слово) , 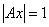
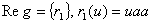
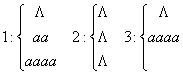 1 и 2 – формальные выводы.
3 – не является формальным выводом. 1 и 2 – формальные выводы.
3 – не является формальным выводом.
4 Предикаты и кванторы.
4.1 Определение предиката.
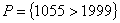
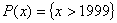 - высказывание, содержащее переменную. - высказывание, содержащее переменную.
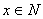 - предметная область предиката. - предметная область предиката.
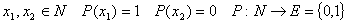 Пусть А – множество объектов произвольной природы (предметная область
предиката).
Пусть А – множество объектов произвольной природы (предметная область
предиката).
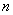 -местный предикат – произвольное отображение -местный предикат – произвольное отображение 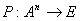 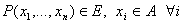
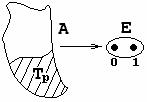 Множество истинности данного предиката Множество истинности данного предиката 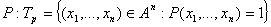
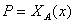 -
- характеристическая
функция от x на множестве
А - совпадает
с предикатами -
- характеристическая
функция от x на множестве
А - совпадает
с предикатами
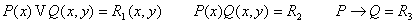

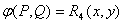 4.2 Понятие квантора.
4.2 Понятие квантора.
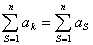 k – связанная переменная
n – свободная переменная k – связанная переменная
n – свободная переменная
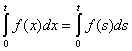 t – свободная, x – связанная. t – свободная, x – связанная.
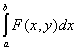 , a,b,y – свободные переменные, x – связанная. , a,b,y – свободные переменные, x – связанная.
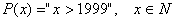
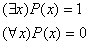
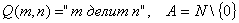
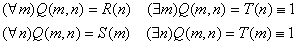 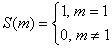
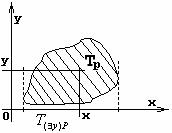
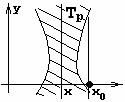
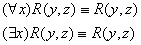 4.3 Геометрическая интерпретация навешивания кванторов.
4.3 Геометрическая интерпретация навешивания кванторов.
| 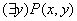
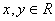
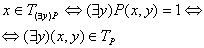 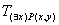 - ортогональная проекция на ось x - ортогональная проекция на ось x
| 
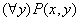
|
Пронесение отрицания через кванторы
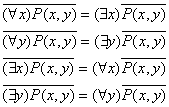 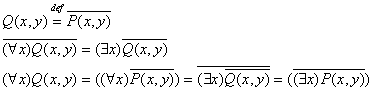 Геометрическое 'доказательство':
Геометрическое 'доказательство':
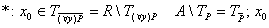 не обладает свойством, что прямая не обладает свойством, что прямая 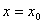 целиком лежит в целиком лежит в 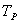
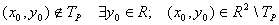
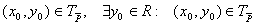
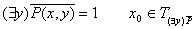 ч.т.д. ч.т.д.
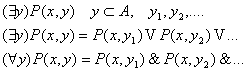
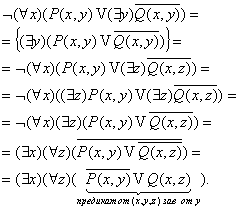
|
|
|
|
|

 1.1.2 Машина Тьюринга - Поста.
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие
элементы алфавита:
1.1.2 Машина Тьюринга - Поста.
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие
элементы алфавита: 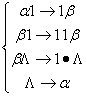
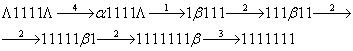
 Теор.: Классы функций
вычислимых на МТ-П, с помощью НАМ и с помощью МНР совпадают.
Пусть
Теор.: Классы функций
вычислимых на МТ-П, с помощью НАМ и с помощью МНР совпадают.
Пусть 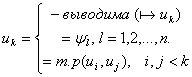
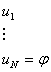
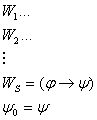
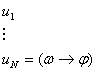
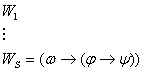
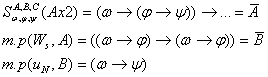 3.1.4 Теорема Дедукции.
Если из
3.1.4 Теорема Дедукции.
Если из
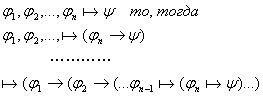
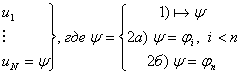 1) и 2а)
1) и 2а) 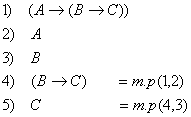 по теореме дедукции
по теореме дедукции 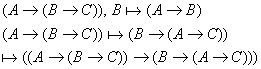 3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
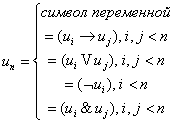
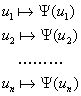 ;
; 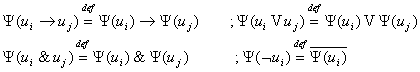 3.2.3 Доказательство теоремы.
3.2.3 Доказательство теоремы.
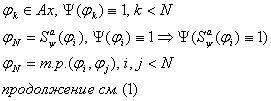
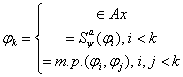 формальный
вывод
формальный
вывод 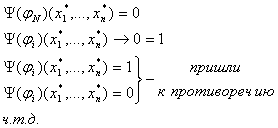 (1)
(1) 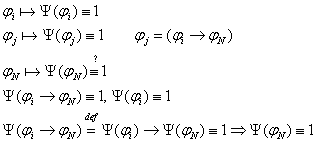 3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем.
3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем. 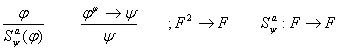 Правило вывода:
Правило вывода:
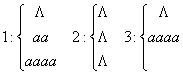 1 и 2 – формальные выводы.
3 – не является формальным выводом.
1 и 2 – формальные выводы.
3 – не является формальным выводом.
 Множество истинности данного предиката
Множество истинности данного предиката 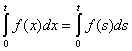 t – свободная, x – связанная.
t – свободная, x – связанная.
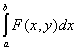 , a,b,y – свободные переменные, x – связанная.
, a,b,y – свободные переменные, x – связанная.
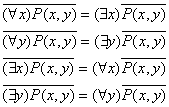
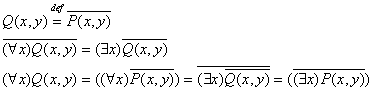 Геометрическое 'доказательство':
Геометрическое 'доказательство':
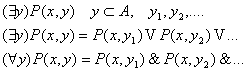
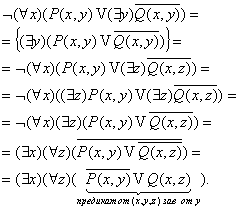
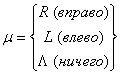 .
.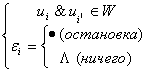
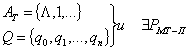
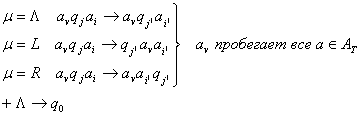 Команда МТП:
Команда МТП: 



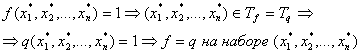 б)
б)
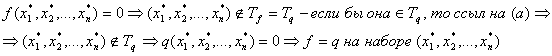 Доказательство:
Доказательство: 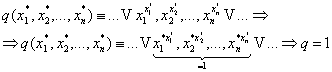 2) Докажем, что
2) Докажем, что 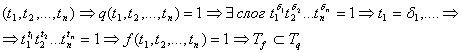 Следовательно
Следовательно 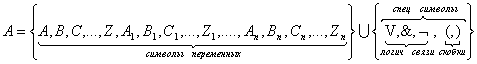 Опр: V – словом в алфавите А, называется любая конечная
упорядоченная последовательность его букв.
Опр: Формативная последовательность слов – конечная
последовательность слов и высказываний
Опр: V – словом в алфавите А, называется любая конечная
упорядоченная последовательность его букв.
Опр: Формативная последовательность слов – конечная
последовательность слов и высказываний 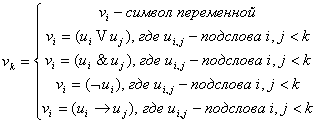 Опр: F – формулой ИВ, называется любое слово, входящее в
какую-нибудь формативную последовательность.
Пример:
Опр: F – формулой ИВ, называется любое слово, входящее в
какую-нибудь формативную последовательность.
Пример: 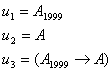
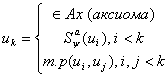 Опр: Выводимый формулой (теоремой) ИВ называется любая формула входящая в
какой-нибудь формальный вывод.
Опр: Выводимый формулой (теоремой) ИВ называется любая формула входящая в
какой-нибудь формальный вывод. 

