 |
РУБРИКИ |
Лекция: Математические модели электромеханических систем в пространстве состояний |
РЕКОМЕНДУЕМ |
||
|
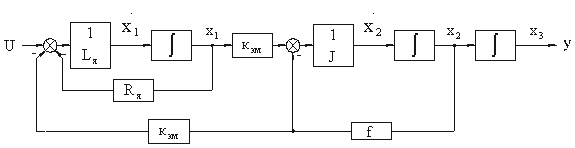
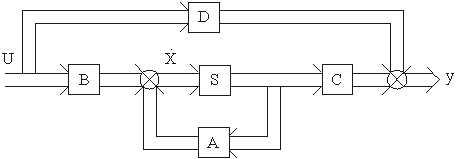
Лекция: Математические модели электромеханических систем в пространстве состоянийЛекция: Математические модели электромеханических систем в пространстве состояний2. Математические модели электромеханических систем в пространстве состояний Способы получения уравнений состояния реальных физических объектов ничем не отличаются от способов описания этих объектов с помощью дифференциальных уравнений. Уравнения состояния записываются на основе физических законов, положенных в основу работы объекта. Рассмотрим электромеханическую систему, состоящую из двигателя постоянного тока с независимым возбуждением, работающего на инерционную нагрузку с вязким трением. Управляющим воздействием для двигателя считаем напряжение на якоре U(t), выходной координатой, угол поворота вала двигателя y(t)=j(t). Уравнение электрической цепи имеет вид где - угловая скорость вала двигателя, - единый электромагнитный коэффициент. Уравнение моментов будет иметь следующий вид где инерции нагрузки, приведенный к валу двигателя, f - коэффициент вязкого трения. Выберем следующие переменные состояния: х1=i, x2=w, x3=j. Получим Запишем эти уравнения относительно переменных Запишем матричные уравнения где Рассмотрим структурную схему электромеханической системы с двигателем постоянного тока, работающего на инерционную нагрузку с вязким трением. Рис. 2.1. Структурная схема электромеханической системы с двигателем постоянного тока Запишем уравнение состояния для механической системы, представляющей собой груз массой m, подвешенный на пружине и соединенный с гидравлическим демпфером. К грузу приложена сила P(t), выходная переменная перемещения x(t), управляющие воздействия U(t)=P(t). Уравнение движения груза получаем из уравнения равновесия сил где сила, f - коэффициент вязкого трения, - сила сопротивления демпфера, - сила сопротивления пружины. Выбираем в качестве переменных состояния x(t) и - перемещение и скорость перемещения соответственно. Рис. 2.2. Механическая система, включающая в своем составе пружину, массу и вязкий демпфер Так как дифференциальное уравнение имеет второй порядок, то и количество переменных состояния будет равно двум. Исходное уравнение движения груза можно записать в виде двух уравнений где U(t)=P(t) - управляющее воздействие. Добавим к этим уравнениям следующее уравнение выхода Эти уравнения представляют собой уравнения состояния приведенной механической системы. Запишем эти уравнения состояния в матричном виде Запишем это уравнение в другом виде где С данным уравнением состояния можно сопоставлять следующую структурную схему, где двойными линиями показаны векторные переменные. Рис. 2.3. Структурная схема Пример: Рассмотрим электрическую цепь и получим уравнение состояния RLC цепи Рис. 2.4. RLC цепь Динамическое поведение этой электрической системы полностью определяется при t³t0, если известны начальные значения: i(t0), e c(t0) и входное напряжение e(t) при t³t0, следовательно, эта система полностью определяется переменными состояния i(t) и ec(t). При указанных переменных состояния i(t) и ec(t) имеем следующие уравнения где Введем следующие обозначения В соответствии с этими обозначениями получаем причем Следовательно, для электрической цепи запишем эту систему в векторно- матричном виде Запишем матричные уравнения где |
|
© 2010 |
|
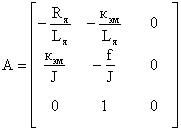 ,
, 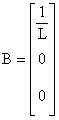 ,
, 
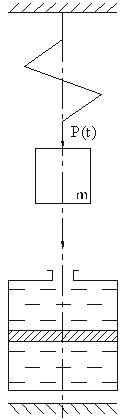
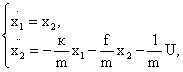
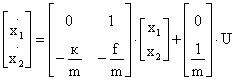 ,
, 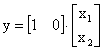 .
. 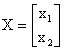 ,
, 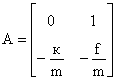 ,
, 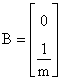 ,
, 
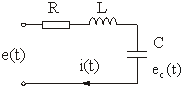
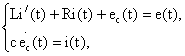
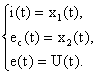
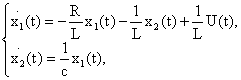
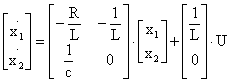 ,
, 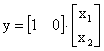 .
. 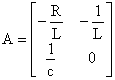 ,
, 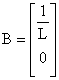 ,
, 