|
|
|
|
Лекция: Метод Крамера
Лекция: Метод Крамера
Министерство рыбного хозяйства
Владивостокский морской колледж
ТЕМА: “ Системы 2-х , 3-х линейных уравнений.
Правило Крамера. ”
г. Владивосток
ОГЛАВЛЕНИЕ.
1.Краткая теория .
2. Методические рекомендации по выполнению заданий.
3.Примеры выполнения заданий.
4.Варианты заданий.
5.Список литературы.
1. КРАТКАЯ ТЕОРИЯ .
________________________________
Пусть дана система линейных уравнений
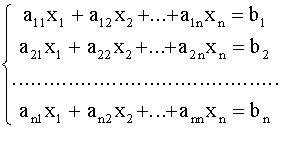 (1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn
ý - называется решением системы (1), если при подстановке этих чисел
вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij
ç, составленный из коэффициентов при неизвестных , называется
определителем системы (1). В зависимости от определителя системы (1) различают
следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может
быть найдено по формулам Крамера : x1= (1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn
ý - называется решением системы (1), если при подстановке этих чисел
вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij
ç, составленный из коэффициентов при неизвестных , называется
определителем системы (1). В зависимости от определителя системы (1) различают
следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может
быть найдено по формулам Крамера : x1=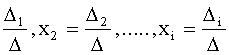 , где
определитель n-го порядка Di ( i=1,2,...,n) получается из
определителя системы путем замены i-го столбца свободными членами b1
, b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо
несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
__________________________________________
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
, где
определитель n-го порядка Di ( i=1,2,...,n) получается из
определителя системы путем замены i-го столбца свободными членами b1
, b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо
несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
__________________________________________
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
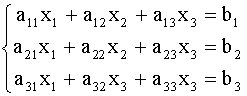 (2).
1. В данной системе составим определитель (2).
1. В данной системе составим определитель  и вычислим.
2. Составить и вычислить следующие определители : и вычислим.
2. Составить и вычислить следующие определители :
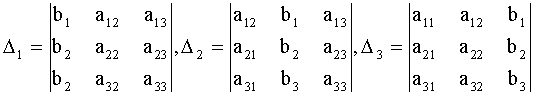 .
3. Воспользоваться формулами Крамера.
.
3. Воспользоваться формулами Крамера.
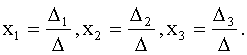 3. ПРИМЕРЫ.
_______________
1.
3. ПРИМЕРЫ.
_______________
1. 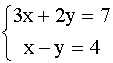 . .
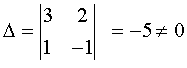
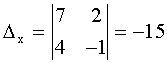 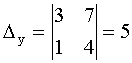
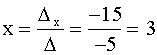 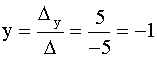 .
Проверка: .
Проверка:
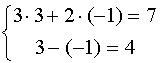 Ответ: ( 3 ; -1 ).
2. Ответ: ( 3 ; -1 ).
2. 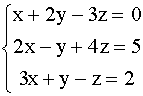
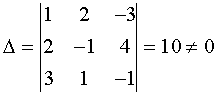

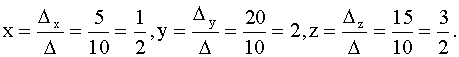 Проверка:
Проверка:
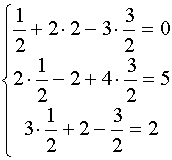 Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
___________________________
ВАРИАНТ 1.
Решить системы:
Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
___________________________
ВАРИАНТ 1.
Решить системы:
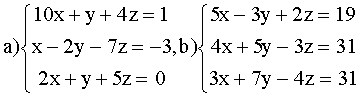 ВАРИАНТ 2.
Решить системы:
ВАРИАНТ 2.
Решить системы:
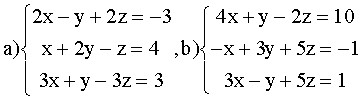 ВАРИАНТ 3.
Решить системы:
ВАРИАНТ 3.
Решить системы:
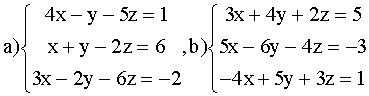 ВАРИАНТ 4.
Решить системы:
ВАРИАНТ 4.
Решить системы:
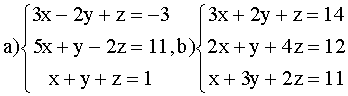 ВАРИАНТ 5.
Решить системы:
ВАРИАНТ 5.
Решить системы:
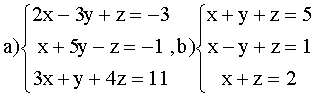 ВАРИАНТ 6.
Решить системы:
ВАРИАНТ 6.
Решить системы:
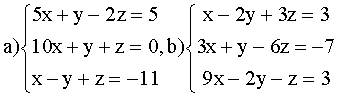 ВАРИАНТ 7.
Решить системы:
ВАРИАНТ 7.
Решить системы:
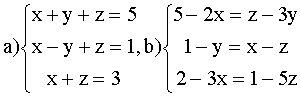 ВАРИАНТ 8.
Решить системы:
ВАРИАНТ 8.
Решить системы:
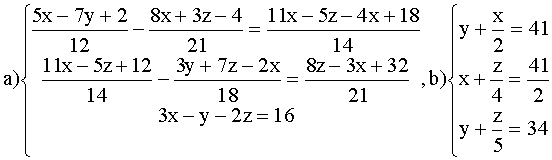 1. Г.И. КРУЧКОВИЧ.
“Сборник задач по курсу высшей математике.”
М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ.
“Высшая математика.”
М. “Высшая школа”, 1985 год.
1. Г.И. КРУЧКОВИЧ.
“Сборник задач по курсу высшей математике.”
М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ.
“Высшая математика.”
М. “Высшая школа”, 1985 год.
|
|
|
|
|

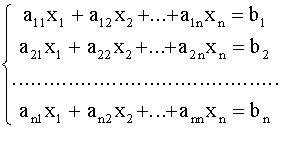 (1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn
ý - называется решением системы (1), если при подстановке этих чисел
вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij
ç, составленный из коэффициентов при неизвестных , называется
определителем системы (1). В зависимости от определителя системы (1) различают
следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может
быть найдено по формулам Крамера : x1=
(1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn
ý - называется решением системы (1), если при подстановке этих чисел
вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij
ç, составленный из коэффициентов при неизвестных , называется
определителем системы (1). В зависимости от определителя системы (1) различают
следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может
быть найдено по формулам Крамера : x1=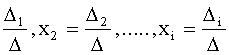 , где
определитель n-го порядка Di ( i=1,2,...,n) получается из
определителя системы путем замены i-го столбца свободными членами b1
, b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо
несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
__________________________________________
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
, где
определитель n-го порядка Di ( i=1,2,...,n) получается из
определителя системы путем замены i-го столбца свободными членами b1
, b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо
несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
__________________________________________
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
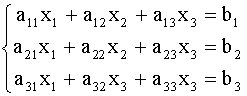 (2).
1. В данной системе составим определитель
(2).
1. В данной системе составим определитель  и вычислим.
2. Составить и вычислить следующие определители :
и вычислим.
2. Составить и вычислить следующие определители :
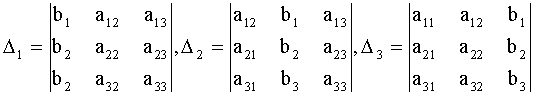 .
3. Воспользоваться формулами Крамера.
.
3. Воспользоваться формулами Крамера.
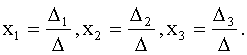 3. ПРИМЕРЫ.
_______________
1.
3. ПРИМЕРЫ.
_______________
1. 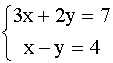 .
.
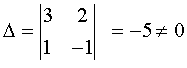
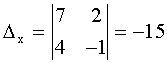
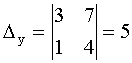
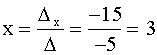
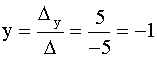 .
Проверка:
.
Проверка:
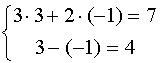 Ответ: ( 3 ; -1 ).
2.
Ответ: ( 3 ; -1 ).
2. 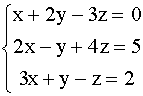
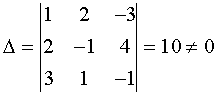

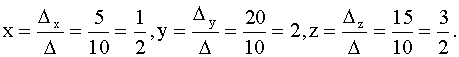 Проверка:
Проверка:
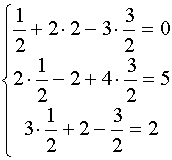 Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
___________________________
ВАРИАНТ 1.
Решить системы:
Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
___________________________
ВАРИАНТ 1.
Решить системы:
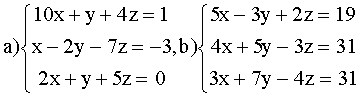 ВАРИАНТ 2.
Решить системы:
ВАРИАНТ 2.
Решить системы:
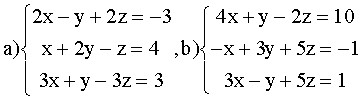 ВАРИАНТ 3.
Решить системы:
ВАРИАНТ 3.
Решить системы:
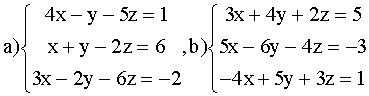 ВАРИАНТ 4.
Решить системы:
ВАРИАНТ 4.
Решить системы:
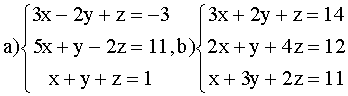 ВАРИАНТ 5.
Решить системы:
ВАРИАНТ 5.
Решить системы:
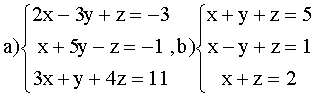 ВАРИАНТ 6.
Решить системы:
ВАРИАНТ 6.
Решить системы:
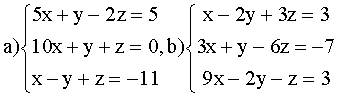 ВАРИАНТ 7.
Решить системы:
ВАРИАНТ 7.
Решить системы:
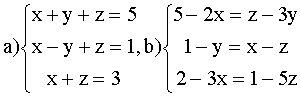 ВАРИАНТ 8.
Решить системы:
ВАРИАНТ 8.
Решить системы:
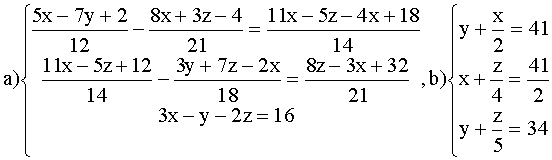 1. Г.И. КРУЧКОВИЧ.
“Сборник задач по курсу высшей математике.”
М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ.
“Высшая математика.”
М. “Высшая школа”, 1985 год.
1. Г.И. КРУЧКОВИЧ.
“Сборник задач по курсу высшей математике.”
М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ.
“Высшая математика.”
М. “Высшая школа”, 1985 год.

