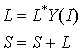|
РУБРИКИ |
Методические указания: Интерполяция |
РЕКОМЕНДУЕМ |
||
|
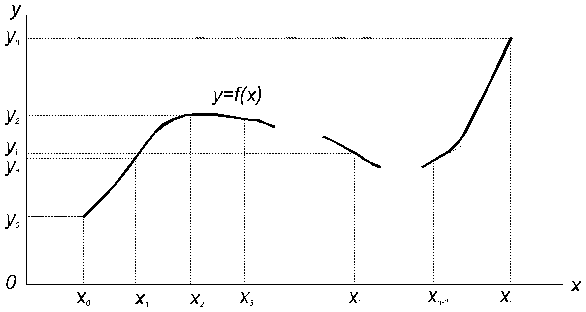
Методические указания: ИнтерполяцияМетодические указания: Интерполяция7 ИНТЕРПОЛЯЦИЯ, ЭКСТРАПОЛЯЦИЯ 7.1 Постановка задачи Предположим, что задано Требуется найти функцию , значения которой при данных значениях абсциссы в точности равны соответствующим ординатам заданных точек: Т.е. нужно найти линию, описываемую уравнением , проходящую через данную точку (рис.7.1).
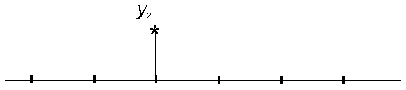
Рис.7.1 Заметим, что здесь приходится различать два случая: 1) интерполяцию (от лат. interpolar — подновлять) — восстановление промежуточных значений функции внутри интервала по ряду известных ее значений; 2) экстраполяцию (лат. приставка extra означает «вне») — когда не вошедшее в исследование значение лежит вне интервала . Очевидно, интерполяция более надежна, чем экстраполяция. Вообще говоря, существует бесконечное число линий, проходящих через заданную точку. Потребуем, чтобы искомая линия была простейшей, т.е. значения функции, задающие эту линию, должны находиться при помощи простейших операций (сложения, умножения). Этому требованию отвечают многочлены (полиномы), т.е. выражения вида: Зная численные значения коэффициентов многочлена, мы можем найти его ординату при любом значении переменной . Наконец, из двух многочленов условимся считать простейшим тот, степень которого ниже. Итак, приходим к задаче о полиномиальной интерполяции: пусть даны различных чисел соответствующих им чисел , требуется найти многочлен наименьшей возможной степени, удовлетворяющий условиям: 7.2 Интерполяционный многочлен Лагранжа для произвольных узлов Для решения предложенной задачи зафиксируем одну ординату , а остальные будем считать равными нулю (рис.7.2), т.е. заданным значениям абсцисс в соответствие значения ординат Из свойств многочленов следует, что многочлен, обращающийся в нуль в разных точках, т.е. имеющий различных корней, должен делиться на каждую из Рис.7.2 а следовательно, и на произведение этих разностей, т.е. его степень не может быть ниже случае многочлен должен иметь вид (7.3) Из условия , таким образом находим (7.4) В полученном выражении никакого особого преимущества не имеет, мы можем приписать эту особую роль любому , т.е. если абсциссам поставить в соответствие значения , указанные в любой из следующих строк: то выражение для многочлена, принимающего при соответствующих значениях абсцисс численные значения, выписанные в одной из строк, будет аналогично рассмотренному, т.е. (7.5) Общее решение является суперпозицией (суммой) частных решений (7.5) (7.6) Это и есть интерполяционный многочлен Лагранжа. По наборам исходных пар (7.1) формула (7.6) позволяет достаточно просто составить «внешний вид» многочлена. Используя обозначение формуле Лагранжа можно придать более сжатый вид. Продифференцируем ; при . (7.8) Формула Лагранжа с учетом (7.7) и (7.8) примет вид: или В рассмотренном случае предполагалось, что точки расположены на отрезке произвольно. Рассмотрим формулу Лагранжа, для равноотстоящих значений абсцисс. 7.3 Интерполяционный многочлен Лагранжа для равностоящих узлов Пусть на отрезке задана система равноотстоящих узлов которыми отрезок делится на равных частей В этом случае интерполяционный многочлен Лагранжа строится на равноотстоящих узлах и имеет более удобный вид. Обозначим .................................................. Т.е. в общем случае: Используя (7.10) и принятое обозначение Учитывая, что Заметим, что в (7.12) ровно строк ( отсутствует); причем численные значения первых строк положительны, а остальные — отрицательны. Используя (7.12), получим: т.е. С учетом (7.11) и (7.13) формула Лагранжа для равноотстоящих узлов примет вид: (7.14) 7.4 Интерполяционный многочлен Ньютона для равноотстоящих узлов На практике часто встречается случай, когда интерполяционная функция подбирается для таблиц с равноотстоящими значениями аргумента Рассмотрим метод построения интерполирующей функции, основанный на вычислении конечных разностей. 7.4.1 Конечные разности Назовем конечными разностями разности между значениями функции в соседних узлах интерполяции: где конечные разности будем называть разностями первого порядка. Из разностей первого порядка получим разности второго порядка: где Повторяя процедуру, получим конечные разности третьего порядка: Для конечных разностей В результате получим таблицу конечных разностей:
............. Используя понятие конечных разностей выведем интерполяционную формулу Ньютона для равноотстоящих узлов 7.4.2 Интерполяционная формула Ньютона Полином перепишем в виде где Т.к. полином выбирается таким образом, чтобы — значения заданной функции совпадали с — значениями интерполирующей функции в узлах, то, полагая найдем 1. Полагая 2. Полагая отсюда 3. Полагая отсюда отсюда Подставив вычисленные значения (7.15) Полученное выражение называется интерполяционной формулой Ньютона для равноотстоящих узлов. 7.5 Погрешность многочленной интерполяции 1. Оценочная формула погрешности метода интерполирования по формуле Лагранжа записывается следующим образом: где значение производной от интерполирующей функции на отрезке (считаем, что функция дифференцируема на отрезке раз). 2. Погрешность при интерполяции полиномом Ньютона оценивается по формуле: 7.6 Пример вычисления значения интерполяционного многочлена Лагранжа Имеется таблица значений функции
Требуется получить значение этой функции в точке , пользуясь интерполяционным многочленом Лагранжа. Для составления программы вычисления одного значения интерполяционного многочлена Лагранжа на ЭВМ воспользуемся формулой (7.9). ввод таблицы x, y
S=0
начало цикла по I от 1 до N
L=1
начало цикла по J от 1 до N
да I=J нет
конец цикла по J
конец цикла по I
вывод Q,S Рис.7.3 Схема алгоритма изображена на рисунке 7.3. В приведенной блок-схеме: N — количество узлов интерполяции; Q — заданное значение аргумента Для набора исходных данных рассматриваемого примера будут получены следующие результаты: 7.7 Контрольные вопросы 1. В чем особенность приближения таблично заданной функции методом интерполирования? 2. Как связана степень интерполяционного многочлена с количеством узлов интерполяции? 3. Как строятся интерполяционные многочлены Лагранжа и Ньютона? В чем особенности этих двух способов интерполяции? 4. В чем состоит различие между интерполяцией и экстраполяцией? 7.8 Задания к лабораторной работе № 7 1. По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа. Построить его график и отметить на нем узловые точки 2. Вычислить одно значение заданной функции для промежуточного значения аргумента интерполяционного многочлена Лагранжа и оценить погрешность интерполяции. 3. Выполнить пункт 2 для интерполяционного многочлена Ньютона. Сравнить полученные результаты. В оформленной работе должны быть приведены графики функций; все составленные алгоритмы или блок-схемы методов, программы и результаты расчетов, ответы на контрольные вопросы. После выполнения заданий необходимо сравнить полученные результаты и сопоставить в них верные цифры.
|
|
© 2010 |
|
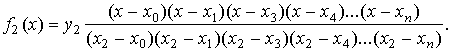
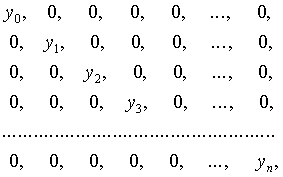
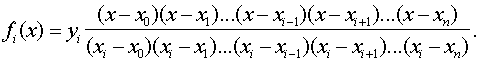
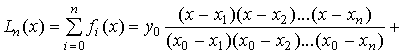
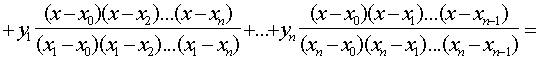
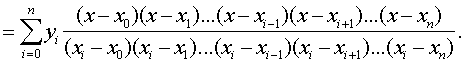
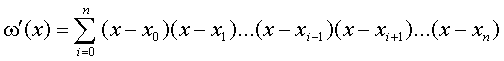
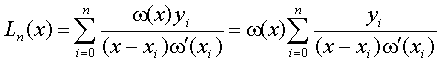
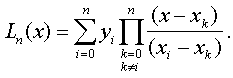 (7.9)
(7.9)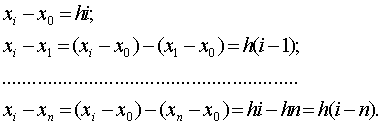 (7.12)
(7.12)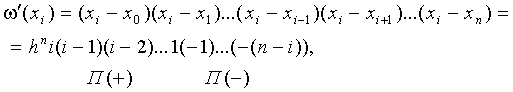
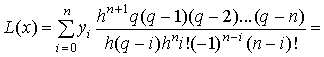
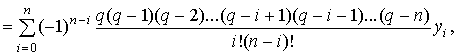
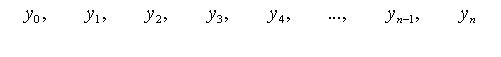
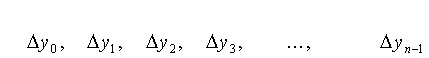




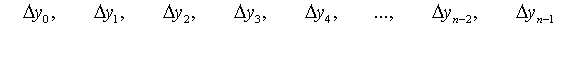
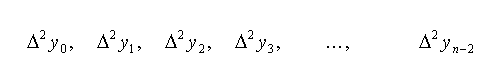
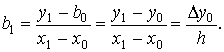
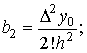 и т.д.
и т.д.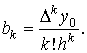
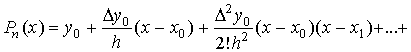

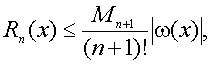 (7.16)
(7.16)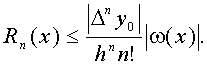 (7.17)
(7.17) ввод N, Q
ввод N, Q