|
РУБРИКИ |
Реферат: Диспут и формула Кардано |
РЕКОМЕНДУЕМ |
||
|
Реферат: Диспут и формула КарданоРеферат: Диспут и формула КарданоДиспут Формула Кардано Мостового Кирилла г. Одесса 1999г Диспут Диспуты в средние века всегда представляли собой интересное зрелище, привлекавшие праздных горожан от мала до велика. Темы диспутов носили разнообразный характер, но обязательно научный. При этом под наукой понимали то, что входило в перечень так называемых семи свободных искусств было, конечно, и богословие. Богословские диспуты были наиболее частыми. Спорили обо всем. Например, о том , приобщать ли мышь к духу святому, если съест причастие, могла ли Кумская сивилла предсказать рождение Иисуса Христа, почему братья и сестры спасителя не причислены к лику святых и т. д. О споре, который должен был произойти между прославленным математиком и не менее прославленным врачом, высказывались лишь самые общие догадки, так как толком никто ничего не знал. Говорили, что один из них обманул другого (кто именно и кого именно, неизвестно). Почти все те, кто собрались на площади имели о математике самые смутные представления, но каждый с нетерпением ожидал начала диспута. Это всегда было интересно, можно было посмеяться над неудачником, независимо от того, прав он или нет. Когда часы на ратуше пробили пять, врата широко распахнулись, и толпа бросилась внутрь собора. По обе стороны от осевой линии, соединяющей вход с алтарем, у двух боковых колонн были воздвигнуты две высокие кафедры, предназначенные для спорщиков. Присутствующие громко шумели, не обращая никакого внимания на то, что находились в церкви. Наконец, перед железной решеткой, отделявшей иконостас от остальной части центрального нефа, появился городской глашатай в черно-фиолетовом плаще и провозгласил: «Достославные граждане города Милана! Сейчас перед вами выступит знаменитый математик Никколо Тарталья из Брении. Его противником должен был быть математик и врач Джеронимо Кардано. Никколо Тарталья обвиняет Кардано в том, что последней в своей книге «Ars magna» опубликовал способ решения уравнения 3-Й степени, принадлежащий ему, Тарталье. Однако сам Кардано на диспут прийти не смог и поэтому прислал своего ученика Луидже Феррари. Итак, диспут объявляется открытым, участники его приглашаются на кафедры». На левую от входа кафедру поднялся неловкий человек с горбатым носом и курчавой бородой, а на противополжную кафедру взошел молодой человек двадцати с небольшим лет, с красивым самоуверенным лицом. Во всей его манере держаться сказывалась полная уверенность в том, что каждый его жест и каждое его слово будут приняты с восторгом. Начал Тарталья. - Уважаемые господа! Вам известно, что 13 лет назад мне удалось найти способ решения уравнения 3-й степени и тогда я, пользуясь этим способом, одержал победу в диспуте с Фиори. Мой способ привлек внимание вашего согражданина Кардано, и он приложил всё своё хитроумное искусство, чтобы выведать у меня секрет. Он не остановился ни перед обманом, ни перед прямым подлогом. Вы знаете также, что 3 года назад в Нюрнберге вышла книга Кардано о правилах алгебры, где мой способ, так бессовестно выкраденный, был сделан достоянием каждого. Я вызвал Кардано и его ученика на состязание. Я предложил решить 31 задачу, столько же было предложено и мне моими противниками. Был определен срок для решения задач – 15 дней. Мне удалось за 7 дней решить большую часть тех задач, которые были составлены Кардано и Феррари. Я напечатал их и послал с курьером в Милан. Однако мне пришлось ждать целых пять месяцев, пока я получил ответы к своим задачам. Они были решены не правильно. Это и дало мне основание вызвать обоих на публичный диспут. Тарталья замолчал. Молодой человек, посмотрев на несчастного Тарталью, произнес: - Уважаемые господа! Мой достойный противник позволил себе в первых же словах своего выступления высказать столько клеветы в мой адрес и в адрес моего учителя, его аргументация была столь голословной, что мне едва ли доставит какой-либо труд опровергнуть первое и показать вам несостоятельность второго. Прежде всего, о каком обмане может идти речь, если Никколо Тарталья совершенно добровольно поделился своим способом с нами обоими? И вот как пишет Джеронимо Кардано о роли моего противника в открытии алгебраического правила. Он говорит, что не ему, Кардано, «а моему другу Тарталье принадлежит честь открытия такого прекрасного и удивительного, превосходящего человеческое остроумие и все таланты человеческого духа. Это открытие есть по истине небесный дар, такое прекрасное доказательство силы ума, его постигнувшего, что уже ничто не может считаться для него недостижимым.» - Мой противник обвинил меня и моего учителя в том, что мы будто бы дали не верное решение его задач. Но как может быть неверным корень уравнения, если подставляя его в уравнение и выполняя все предписанные в этом уравнении действия, мы приходим к тождеству? И уже если сеньор Тарталья хочет быть последовательным, то он должен был ответить на замечание, почему мы, укравшие, но его словами, его изобретение и использовавши его для решения предложенных задач, получили неверное решение. Мы – мой учитель и я – не считаем, однако изобретение синьора Тартальи маловажным. Это изобретение замечательно. Более того, я, опираясь в значительной мере на него, нашел способ решения уравнения 4-й степени, и в «Ars magna» мой учитель говорит об этом. Что же хочет от нас сеньор Тарталья? Чего он добивается диспутом? - Господа, господа, - закричал Тарталья, - я прошу вас выслушать меня! Я не отрицаю того, что мой молодой противник очень силен в логике и красноречии. Но этим нельзя заменить истинное математическое доказательство. Задачи, которые я дал Кардано и Феррари, решены не правильно, но и я докажу это. Действительно, возьмем, например, уравнение из числа решавшихся. Оно, как известно . В церкви поднялся невообразимый шум, поглотивший полностью окончание фразы, начатой незадачливым математиком. Ему не дали продолжать. Толпа, требовала от него, чтобы он замолчал, и чтобы очередь была предоставлена Феррари. Тарталья, видя, что продолжение спора совершенно бесполезно, поспешно опустился с кафедры и вышел через северный притвор на площадь. Толпа бурно приветствовала «победителя» диспута Луиджи Феррари. .Так закончился этот спор, который и сейчас продолжает вызывать все новые и новые споры. Кому в действительности принадлежит способ решения уравнения 3-й степени? Мы говорим сейчас – Никколо Тарталье. Он открыл , а Кардано выманил у него это открытие. И если сейчас мы называем формулу, представляющую корни уравнения 3-й степени через его коэффициенты, формулой Кардано, то это - историческая несправедливость. Однако, несправедливость ли? Как подсчитать меру участия в открытии каждого из математиков? Может быть, со временем кто- то и сможет ответить на этот вопрос совершенно точно, а может быть это останется тайной .
Формула КарданоЕсли воспользоваться современным математическим языком и современной символикой, то вывод формулы Кардано может быть найден с помощью следующих в высшей степени элементарных соображений: Пусть нам дано общее уравнение 3-й степени: ax3+3bx2+3cx+d=0 (1)
Если положить где Введем новое неизвестное U с помощью равенства Внося это выражение в (2), получим Отсюда следовательно Если числитель и знаменатель второго слагаемого умножить на выражение и учесть, получающееся в результате выражение для u оказывается симметричным относительно знаков «+» и «-», то окончательно получим (Произведение кубических радикалов в последнем равенстве должно равняться p ). Это и есть знаменитая формула Кардано. Если перейти от y вновь к x, то получим формулу, определяющую корень общего уравнения 3-й степени. Молодой человек, так безжалостно обошедшийся с Тарталья, разбирался в математике столь же легко, как и в правах неприхотливой тайны. Феррари находит способ решения уравнения 4-й степени. Кардано поместил этот способ в свою книгу. Что же представляет собой этот способ? Пусть – общее уравнение 4-й степени. Если положить то уравнение (1) можно привести к виду где p,q,r – некоторые коэффициенты, зависящие от a,b,c,d,e. Легко видеть, что это уравнение можно записать в таком виде: В самом деле, достаточно раскрыть скобки, тогда все члены, содержащие t, взаимно уничтожается, и мы возвратимся к уравнению (2). Выберем параметр t так ,чтобы правая часть уравнения (3) была полным квадратом относительно y. Как известно, необходимым и достаточным условием этого является обращение в нуль дискриминанта из коэффициентов трехчлена (относительно y), стоящего справа: Получили полное кубическое уравнение, которое мы уже можем решить. Найдем какой либо его корень и внесем его в уравнение (3), теперь примет вид Отсюда Это квадратное уравнение. Решая его, можно найти корень уравнения(2), а следовательно и (1). За 4 месяца до смерти Кардано закончил свою автобиографию, которою он напряженно писал весь последний год и которая должна была подвести итог его сложной жизни. Он чувствовал приближение смерти. По некоторым сведениям его собственный гороскоп связывал его кончину с 75- летием. Он умер 21сентября 1576г. за 2 дня до годовщины. Имеется версия, что он покончил с собой в ожидании неминуемой смерти или даже чтобы подтвердить гороскоп. В любом случае Кардано – астролог относился к гороскопу серьезно.
Замечание о формуле КарданоПроанализируем формулу для решения уравнения При вычислении x нам приходится извлекать в начале квадратный корень, а затем кубический. Мы сможем извлечь квадратный корень, оставаясь в вещественной области, если Два значения квадратного корня, отличающихся знаком, фигурируют в разных слагаемых для x. Значения кубического корня в вещественной области единственно и получается единственный вещественный корень x при . Исследуя график кубического трехчлена ,нетрудно убедиться, что он в самом деле имеет единственный вещественный корень при имеется три вещественных корня. При имеется двукратный вещественный корень и однократный, а при -трехкратный корень x=0. Продолжим исследование формулы при . Оказывается. Что если при этом уравнение с целыми коэффициентами имеет целочисленный корень, при вычислении его по формуле могут возникнуть промежуточные иррациональности. Например, уравнение имеет единственный корень (вещественный) – x=1. Формула Кардано дает для этого единственного вещественного корня выражение Значит, любое доказательство предполагает использование того, что это выражение является корнем уравнения . Если же не угадать того, при преобразовании будут возникать неистребимые кубические радикалы. О проблеме Кардано – Тартальи вскоре забыли. Формулу для решения кубического уравнения связали с «Великим искусством» и постепенно стали называть формулой Кардано. У многих возникало желание восстановить истинную картину событий в ситуации, когда их участники несомненно не говорили всей правды. Для многих было важно установить степень вины Кардано. К концу XIX века часть дискуссий стала носить характер серьезных историко-математических исследований. Математики поняли, какую большую роль в конце XVI века сыграли работы Кардано. Стало ясно то, что еще раньше отмечал Лейбниц: «Кардано был великим человеком при всех его недостатках; без них он был бы совершенством». |
|
© 2010 |
|
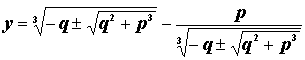
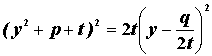 .
.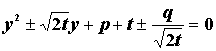 .
.