 |
РУБРИКИ |
Реферат: Граничные условия общего вида |
РЕКОМЕНДУЕМ |
||
|
Реферат: Граничные условия общего видаРеферат: Граничные условия общего видаПлан. 1. Сопряженный оператор. 2. Сопряженная однородная задача. 3. Условия разрешимости. Сопряженный оператор. Обозначим через где собой непрерывные функции в промежутке . Если - дважды непрерывно дифференцируемые на функции, то имеем: Как и в предыдущем параграфе, интегрирование соотношения (2) по частям дает: (3) Обозначим дифференциальный оператор, входящий в подынтегральное выражение в правой части (3) через , т.е. (4) При этом соотношение (3) перепишется так: Оператор сопряженным по отношению к оператору . Умножая соотношение (4) на и интегрируя полученный результат по частям, по отношению к оператору . Таким образом, операторы и сопряжены. Как и в предыдущем параграфе, дифференциальное уравнение: будем называть сопряженным дифференциальному уравнению: Если же оператор дифференциальное уравнение будем называть сопряженными. Сравнивая выражения (1) и (5), приходим к выводу, что только, когда: Таким образом, оператор При этом: Так как любое дифференциальное уравнение вида (7) можно преобразовать в самосопряженную форму, умножив на функцию . Дифференцируя соотношение (5) по Правая часть этой формулы может быть записана как: (9) где Отметим, что: матрица -невырожденная. Подстановка выражения (9) в соотношение (8) дает: Сопряженная однородная задача. Введем следующее невырожденное линейное преобразование где Заметим, что указанное преобразование может быть выполнено бесчисленным множеством способов, в зависимости от выбора матрицы А. При заданном ненулевом векторе последние строки матрицы А можно выбрать так, чтобы придать любые требуемые значения компонентам . Это замечание используется в дальнейшем при нахождении вида сопряженных граничных условий. Поскольку , мы можем обратить преобразование (12) и получить: При этом (11) можно переписать как: или где Билинейная форма соотношении (13) называется каноническим представлением билинейной формы в правой части тождества (11). Для того чтобы найти граничные условия сопряженной задачи, положим в соотношении (13) Из формулы (21) следует, что однородные граничные условия, эквивалентны равенствам: С учетом равенств (16) и (17) соотношение (15) принимает вид: При ненулевом векторе последние две строки матрицы А могут быть выбраны так, чтобы компоненты и требуемые значения, лишь бы и нуль одновременно. В частности, нижние строки матрицы А можно выбрать из условия из соотношения (11) следует, что . Аналогичным образом, нижние строки матрицы А можно выбрать так, чтобы выполнялись равенства . При этом из соотношения (11) вытекает, что . Таким образом, задача, сопряженная задаче (19) имеет вид: где связаны с компонентами вектора соотношением (14). Краевая задача (19) называется самосопряженной тогда и только тогда, когда каждая из двух компонент и комбинацией , т.е. пропорциональна Один из определителей: матриц-блоков должен быть отличным от нуля. Чтобы иметь возможность сравнить эти результаты с теми. которые были получены в предыдущем параграфе, предположим. что . Далее, выберем такие и матрицы А были линейно независимы. Например, положим При этом матрица А примет вид: Из формулы (19) следует, что Тогда Подставляя матрицы (20) и (9) в соотношение (14) имеем (14а): Следовательно, граничные условия сопряженной задачи имеют вид: (22) (23) Для того, чтобы краевые задачи были самосопряженными необходимо, чтобы и чтобы каждая из компонент и комбинацией . Как указывалось выше, тогда и только тогда, когда . При этом условия (21) и (20) принимают вид: Разрешая равенства относительно Сравнивая граничные условия (24) и (25), заключаем, что они совпадают тогда и только тогда, когда: Краевая задача при самосопряжена тогда и только тогда, когда выполнены соотношения (24) и равенство . Условие разрешимости. Определив сопряженную краевую задачу, вернемся к решению неоднородной задачи. Используя определение (25), перепишем формулу Грина в виде: тогда из соотношения (27) вытекает, что условие разрешимости имеет вид: Для того, чтобы сравнить условие (27) с условием разрешимости, используем связь и , описываемую формулой (14а) т.е.: При этом соотношение (27) принимает вид: Если иметь дело с граничными условиями общего вида можно выразить какие-либо два из граничных значений через два других. |
|
© 2010 |
|
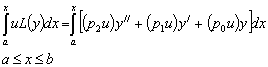 (2)
(2)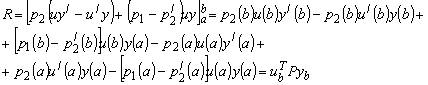
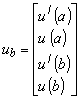
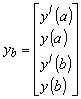
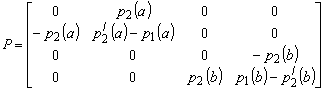 (10)
(10)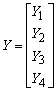

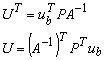 (14)
(14)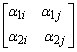
 (21).
(21). (22)
(22)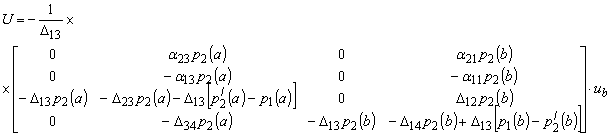
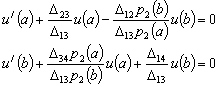 (24)
(24)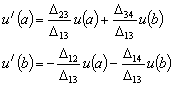 (25)
(25)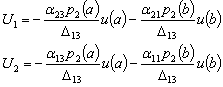 (28)
(28)