|
|
|
|
Реферат: Кривые и поверхности второго порядка
Реферат: Кривые и поверхности второго порядка
ЭЛЛИПС.
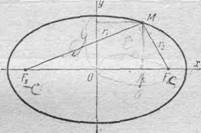
Эллипсом называется геометрическое место точек, для которых сумма расстояний от
двух фиксированных точек плоскости, называемых фокусами, есть постоянная
величина; требуется, чтобы эта постоянная была больше расстояния между
фокусами. Фокусы эллипса принято обозначать через F1 и F2.
Пусть М—произвольная точка эллипса с фокусами F1 и
F2. Отрезки F1М и F2М (так
же как и длины этих отрезков) называются фокальными радиусами точки
М. Постоянную сумму фокальных радиусов точки эллипса принято обозначать
через 2а. Таким образом, для любой точки М эллипса имеем:
F1М + F2М = 2а.
Расстояние F1 и F2 между фокусами обозначают через 2с.
Пусть дан какой-нибудь эллипс с фокусами F1, F2.
Возьмем на плоскости произвольную точку М и обозначим ее координаты
через х и у. Обозначим, далее, через r1 и
r2 расстояния от точки М до фокусов (r1 =
F1М, r2 = F2М). Точка М будет
находиться на данном эллипсе в том и только в том случае, когда
r1 + r2 = 2а.
Чтобы получить искомое уравнение, нужно в равенстве заменить переменные r
1 и r2 их выражениями через координаты х, у.
Заметим, что так как F1 F2 = 2с и так как фокусы
F1 и F2 расположены на оси Ох
симметрично относительно начала координат, то они имеют соответственно
координаты (—с; 0) и (+с; 0); приняв это во внимание находим:
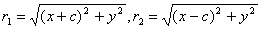 Заменяя r1 и r2, получаем:
Заменяя r1 и r2, получаем:
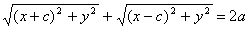 Это и есть уравнение рассматриваемого эллипса, так как ему удовлетворяют
координаты точки
М (х; у), когда точка М лежит на этом эллипсе. Возведём обе части
равенства в квадрат, получим:
Это и есть уравнение рассматриваемого эллипса, так как ему удовлетворяют
координаты точки
М (х; у), когда точка М лежит на этом эллипсе. Возведём обе части
равенства в квадрат, получим:
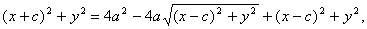 или
или
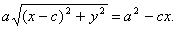 Возводя в квадрат обе части последнего равенства, найдем:
а2х2 — 2а2сх + а2с2 + а2у2 = а4 — 2а2сх + с2х2 ,
откуда
(а2—с2)х2 + а2у2 = а2(а2—с2).
Здесь мы введем в рассмотрение новую величину
Возводя в квадрат обе части последнего равенства, найдем:
а2х2 — 2а2сх + а2с2 + а2у2 = а4 — 2а2сх + с2х2 ,
откуда
(а2—с2)х2 + а2у2 = а2(а2—с2).
Здесь мы введем в рассмотрение новую величину
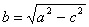 ;
а>с, следовательно, а2—с2>0 и величина b—вещественна.
b2 = a2—c2,
тогда
b2x2 + a2y2 = a2b2 ,
или ;
а>с, следовательно, а2—с2>0 и величина b—вещественна.
b2 = a2—c2,
тогда
b2x2 + a2y2 = a2b2 ,
или
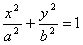 .
Это уравнение называется каноническим уравнением эллипса.
Уравнение .
Это уравнение называется каноническим уравнением эллипса.
Уравнение
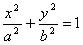 ,
определяющее эллипс в некоторой системе декартовых прямоугольных координат, есть
уравнение второй степени; таким образом, эллипс есть линия второго порядка.
Эксцентриситетом эллипса называется отношение расстояния между фокусами
этого эллипса к длине его большой оси; обозначив эксцентриситет буквой
ε, получаем: ,
определяющее эллипс в некоторой системе декартовых прямоугольных координат, есть
уравнение второй степени; таким образом, эллипс есть линия второго порядка.
Эксцентриситетом эллипса называется отношение расстояния между фокусами
этого эллипса к длине его большой оси; обозначив эксцентриситет буквой
ε, получаем:
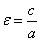 .
Так как с<a, то ε<1, т. е. эксцентриситет каждого эллипса меньше единицы.
Заметим, что c2 = a2— b2; поэтому .
Так как с<a, то ε<1, т. е. эксцентриситет каждого эллипса меньше единицы.
Заметим, что c2 = a2— b2; поэтому
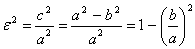 ;
отсюда ;
отсюда
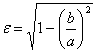 и и 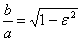 Следовательно, эксцентриситет определяется отношением осей эллипса, а
отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом,
эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к
единице, тем меньше 1— ε2, тем меньше, следовательно,
отношение
Следовательно, эксцентриситет определяется отношением осей эллипса, а
отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом,
эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к
единице, тем меньше 1— ε2, тем меньше, следовательно,
отношение 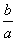 ; значит,
чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности
b=a и ε=0.
Рассмотрим какой-нибудь эллипс и введем декартову прямоугольную систему
координат так, чтобы этот эллипс определялся каноническим уравнением ; значит,
чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности
b=a и ε=0.
Рассмотрим какой-нибудь эллипс и введем декартову прямоугольную систему
координат так, чтобы этот эллипс определялся каноническим уравнением
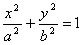 Предположим, что рассматриваемый эллипс не является окружностью, т. е. что
а≠b и, следовательно, ε=0. Предположим еще, что этот
эллипс вытянут в направлении оси Ох, т. е. что а>b.
Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично
относительно центра на расстоянии
Предположим, что рассматриваемый эллипс не является окружностью, т. е. что
а≠b и, следовательно, ε=0. Предположим еще, что этот
эллипс вытянут в направлении оси Ох, т. е. что а>b.
Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично
относительно центра на расстоянии 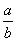 от него, называются директрисами эллипса.
Уравнения директрис в выбранной системе координат имеют вид
от него, называются директрисами эллипса.
Уравнения директрис в выбранной системе координат имеют вид
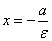 и и 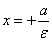 .
Первую из них мы условимся называть левой, вторую—правой. Так как для эллипса
ε<1, то .
Первую из них мы условимся называть левой, вторую—правой. Так как для эллипса
ε<1, то 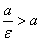 . Отсюда следует, что правая директриса расположена правее правой вершины
эллипса; аналогично, левая директриса расположена левее его левой вершины.
Частным случаем эллипса является окружность. Её уравнение имеет вид:
х2 + у2 = R2.
ГИПЕРБОЛА.
. Отсюда следует, что правая директриса расположена правее правой вершины
эллипса; аналогично, левая директриса расположена левее его левой вершины.
Частным случаем эллипса является окружность. Её уравнение имеет вид:
х2 + у2 = R2.
ГИПЕРБОЛА.
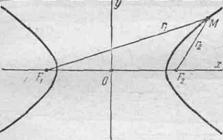 Гиперболой называется
геометрическое место точек, для которых разность расстояний от двух
фиксированных точек плоскости, называемых фокусами, есть постоянная величина;
указанная разность берется по абсолютному значению; кроме того,
требуется, чтобы она была меньше расстояния между фокусами и отлична от
нуля. Фокусы гиперболы принято обозначать через F1 и
F2, а расстояние между ними—через 2с.
Пусть М—произвольная точка гиперболы с фокусами F1 и
F2. Отрезки F1М и F2М (так
же, как и длины этих отрезков) называются фокальными радиусами точки
М и обозначаются через r1 и r2 (r1
= F1М, r2= F2М). По определению гиперболы
разность фокальных радиусов ее точки М есть постоянная величина;
эту постоянную принято обозначать через 2а.
Пусть дана какая-нибудь гипербола с фокусами F1 и F2
. Возьмем на плоскости произвольную точку М и обозначим ее
координаты через х и у, а фокальные радиусы F1М
и F2М через r1 и r2.
Точка М будет находиться на (данной) гиперболе в том и только в том
случае, когда
r1— r2= ±2а.
Так как F1 F2=2с и так как фокусы F1
и F2 расположены на оси Ох симметрично относительно
начала координат, то они имеют соответственно координаты (—с; 0) и (+с;
0); приняв это во внимание находим: Гиперболой называется
геометрическое место точек, для которых разность расстояний от двух
фиксированных точек плоскости, называемых фокусами, есть постоянная величина;
указанная разность берется по абсолютному значению; кроме того,
требуется, чтобы она была меньше расстояния между фокусами и отлична от
нуля. Фокусы гиперболы принято обозначать через F1 и
F2, а расстояние между ними—через 2с.
Пусть М—произвольная точка гиперболы с фокусами F1 и
F2. Отрезки F1М и F2М (так
же, как и длины этих отрезков) называются фокальными радиусами точки
М и обозначаются через r1 и r2 (r1
= F1М, r2= F2М). По определению гиперболы
разность фокальных радиусов ее точки М есть постоянная величина;
эту постоянную принято обозначать через 2а.
Пусть дана какая-нибудь гипербола с фокусами F1 и F2
. Возьмем на плоскости произвольную точку М и обозначим ее
координаты через х и у, а фокальные радиусы F1М
и F2М через r1 и r2.
Точка М будет находиться на (данной) гиперболе в том и только в том
случае, когда
r1— r2= ±2а.
Так как F1 F2=2с и так как фокусы F1
и F2 расположены на оси Ох симметрично относительно
начала координат, то они имеют соответственно координаты (—с; 0) и (+с;
0); приняв это во внимание находим:
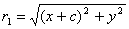 , , 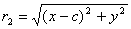 .
Заменяя r1 и r2, получаем: .
Заменяя r1 и r2, получаем:
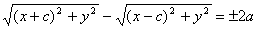 .
Это и есть уравнение рассматриваемой гиперболы, так как ему удовлетворяют
координаты точки М (х; у), когда точка М лежит на гиперболе.
Возведём обе части равенства в квадрат; получим: .
Это и есть уравнение рассматриваемой гиперболы, так как ему удовлетворяют
координаты точки М (х; у), когда точка М лежит на гиперболе.
Возведём обе части равенства в квадрат; получим:
 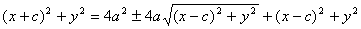 , , или
или
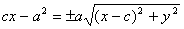 .
Возводя в квадрат обе части этого равенства, найдем:
c2x2 – 2a2cx + a4 = a2x2 – 2a2cx + a2c2 + a2y2 ,
откуда
(c2 – a2)x2 – a2y2 = a2(c2 – a2) .
Здесь мы введем в рассмотрение новую величину .
Возводя в квадрат обе части этого равенства, найдем:
c2x2 – 2a2cx + a4 = a2x2 – 2a2cx + a2c2 + a2y2 ,
откуда
(c2 – a2)x2 – a2y2 = a2(c2 – a2) .
Здесь мы введем в рассмотрение новую величину
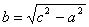 ;
с>a, следовательно, с2—а2>0 и величина b—вещественна.
b2= с2—а2,
тогда
b2x2 — a2y2 = a2b2 ,
или ;
с>a, следовательно, с2—а2>0 и величина b—вещественна.
b2= с2—а2,
тогда
b2x2 — a2y2 = a2b2 ,
или
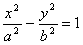 .
Уравнение .
Уравнение
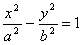 ,
определяющее гиперболу в некоторой системе декартовых прямоугольных координат,
есть уравнение второй степени; таким образом, гипербола есть линия второго
порядка.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами
этой гиперболы к расстоянию между ее вершинами; обозначив эксцентриситет
буквой ε, получим: ,
определяющее гиперболу в некоторой системе декартовых прямоугольных координат,
есть уравнение второй степени; таким образом, гипербола есть линия второго
порядка.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами
этой гиперболы к расстоянию между ее вершинами; обозначив эксцентриситет
буквой ε, получим:
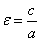 .
Так как для гиперболы с>a, то ε>1; т. е.
эксцентриситет каждой гиперболы больше единицы. Заметив, что c2
= a2+ b2, находим: .
Так как для гиперболы с>a, то ε>1; т. е.
эксцентриситет каждой гиперболы больше единицы. Заметив, что c2
= a2+ b2, находим:
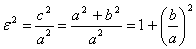 ;
отсюда ;
отсюда
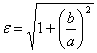 и и 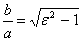 .
Следовательно, эксцентриситет определяется отношением .
Следовательно, эксцентриситет определяется отношением 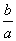 , а отношение
, а отношение 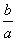 в
свою очередь определяется эксцентриситетом. Таким образом, эксцентриситет
гиперболы характеризует форму ее основного прямоугольника, а значит, и форму
самой гиперболы.
Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше ε
2—1, тем меньше, следовательно, отношение в
свою очередь определяется эксцентриситетом. Таким образом, эксцентриситет
гиперболы характеризует форму ее основного прямоугольника, а значит, и форму
самой гиперболы.
Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше ε
2—1, тем меньше, следовательно, отношение 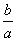 ; значит, чем меньше эксцентриситет гиперболы, тем более вытянут ее
основной прямоугольник (в направлении оси, соединяющей вершины). В случае
равносторонней гиперболы a=b и ε=√2.
Рассмотрим какую-нибудь гиперболу и введем декартову прямоугольную систему
координат так, чтобы эта гипербола определялась каноническим уравнением
; значит, чем меньше эксцентриситет гиперболы, тем более вытянут ее
основной прямоугольник (в направлении оси, соединяющей вершины). В случае
равносторонней гиперболы a=b и ε=√2.
Рассмотрим какую-нибудь гиперболу и введем декартову прямоугольную систему
координат так, чтобы эта гипербола определялась каноническим уравнением
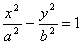 .
Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и
расположенные симметрично относительно центра на расстоянии .
Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и
расположенные симметрично относительно центра на расстоянии 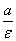 от него, называются директрисами гиперболы.
Уравнения директрис в выбранной системе координат имеют вид
от него, называются директрисами гиперболы.
Уравнения директрис в выбранной системе координат имеют вид
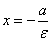 и и 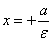 .
Первую из них мы условимся называть левой, вторую —правой.
Так как для гиперболы ε >1, то .
Первую из них мы условимся называть левой, вторую —правой.
Так как для гиперболы ε >1, то 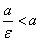 .
Отсюда следует, что правая директриса расположена между центром и правой
вершиной гиперболы; аналогично, левая директриса расположена между центром
и левой вершиной.
ПАРАБОЛА. .
Отсюда следует, что правая директриса расположена между центром и правой
вершиной гиперболы; аналогично, левая директриса расположена между центром
и левой вершиной.
ПАРАБОЛА.
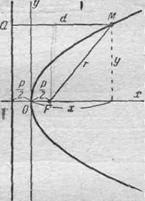 Параболой называется
геометрическое место точек, для каждой из которых расстояние до некоторой
фиксированной точки плоскости, называемой фокусом, равно расстоянию до
некоторой фиксированной прямой, называемой директрисой (предполагается,
что эта прямая не проходит через фокус).
Фокус параболы принято обозначать буквой F, расстояние от фокуса до
директрисы—буквой p. Величину р называют параметром параболы.
Пусть дана какая-нибудь парабола. Возьмем на плоскости произвольную точку М
и обозначим ее координаты через х и у. Обозначим далее через
r расстояние от точки М до фокуса (r=FM), через d—
расстояние от точки М до директрисы. Точка М будет находиться
на (данной) параболе в том и только в том случае, когда
r=d.
Чтобы получить искомое уравнение, нужно заменить переменные r и d
их выражениями через текущие координаты х, у.
Заметим, что фокус F имеет координаты Параболой называется
геометрическое место точек, для каждой из которых расстояние до некоторой
фиксированной точки плоскости, называемой фокусом, равно расстоянию до
некоторой фиксированной прямой, называемой директрисой (предполагается,
что эта прямая не проходит через фокус).
Фокус параболы принято обозначать буквой F, расстояние от фокуса до
директрисы—буквой p. Величину р называют параметром параболы.
Пусть дана какая-нибудь парабола. Возьмем на плоскости произвольную точку М
и обозначим ее координаты через х и у. Обозначим далее через
r расстояние от точки М до фокуса (r=FM), через d—
расстояние от точки М до директрисы. Точка М будет находиться
на (данной) параболе в том и только в том случае, когда
r=d.
Чтобы получить искомое уравнение, нужно заменить переменные r и d
их выражениями через текущие координаты х, у.
Заметим, что фокус F имеет координаты 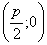 ; приняв это во внимание, находим: ; приняв это во внимание, находим:
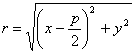 .
Обозначим через Q основание перпендикуляра, опущенного из точки М
на директрису. Очевидно, точка Q имеет координаты .
Обозначим через Q основание перпендикуляра, опущенного из точки М
на директрису. Очевидно, точка Q имеет координаты 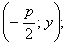 отсюда, получаем:
отсюда, получаем:
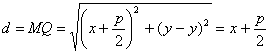
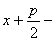 число
положительное; это следует из того, что М (х; у) должна находиться с
той стороны от директрисы, где находится фокус, т. е. должно быть число
положительное; это следует из того, что М (х; у) должна находиться с
той стороны от директрисы, где находится фокус, т. е. должно быть 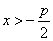 , откуда
, откуда 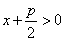 .
Заменяя r и d, найдем .
Заменяя r и d, найдем
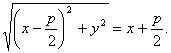 Это и есть уравнение рассматриваемой параболы, так как ему удовлетворяют
координаты точки
М (х; у), когда точка М лежит на данной параболе.
Возведем обе части равенства в квадрат; получим:
Это и есть уравнение рассматриваемой параболы, так как ему удовлетворяют
координаты точки
М (х; у), когда точка М лежит на данной параболе.
Возведем обе части равенства в квадрат; получим:
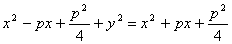 или
у2=2рх.
Это уравнение называется каноническим уравнением параболы. Уравнение
у2=2рх, определяющее параболу в некоторой системе декартовых
прямоугольных координат, есть уравнение второй степени; таким образом,
парабола есть линия второго порядка.
Министерство образования РФ
Пензенская Государственная Архитектурно-Строительная
Академия
РЕФЕРАТ
Тема: «Кривые и поверхности второго порядка»
Выполнил: Богданович Ольга
Специальность: ОБД
Обозначение: 240400 Группа: ОБД-11
Проверил: Фадеева Г.Д.
Оценка:
Пенза – 2000.
Кривые
второго
порядка
Поверхности
второго
порядка
Эллипсоид
или
у2=2рх.
Это уравнение называется каноническим уравнением параболы. Уравнение
у2=2рх, определяющее параболу в некоторой системе декартовых
прямоугольных координат, есть уравнение второй степени; таким образом,
парабола есть линия второго порядка.
Министерство образования РФ
Пензенская Государственная Архитектурно-Строительная
Академия
РЕФЕРАТ
Тема: «Кривые и поверхности второго порядка»
Выполнил: Богданович Ольга
Специальность: ОБД
Обозначение: 240400 Группа: ОБД-11
Проверил: Фадеева Г.Д.
Оценка:
Пенза – 2000.
Кривые
второго
порядка
Поверхности
второго
порядка
Эллипсоид
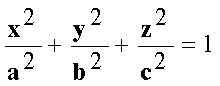 Однополостный гиперболоид
Однополостный гиперболоид
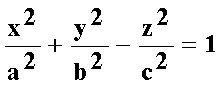 Двухполостный гиперболоид
Двухполостный гиперболоид
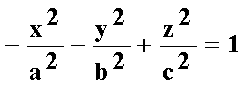 Конус
Конус
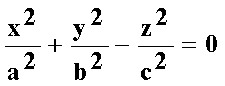 Эллиптический параболоид
Эллиптический параболоид
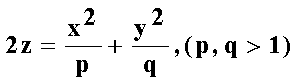 Гиперболический параболоид
Гиперболический параболоид
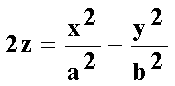 Эллиптический цилиндр
Эллиптический цилиндр
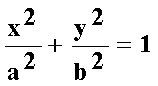 Гиперболический цилиндр
Гиперболический цилиндр
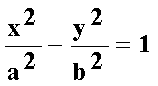 Параболический цилиндр
Параболический цилиндр
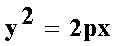
|
|
|
|
|

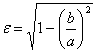 и
и  Гиперболой называется
геометрическое место точек, для которых разность расстояний от двух
фиксированных точек плоскости, называемых фокусами, есть постоянная величина;
указанная разность берется по абсолютному значению; кроме того,
требуется, чтобы она была меньше расстояния между фокусами и отлична от
нуля. Фокусы гиперболы принято обозначать через F1 и
F2, а расстояние между ними—через 2с.
Пусть М—произвольная точка гиперболы с фокусами F1 и
F2. Отрезки F1М и F2М (так
же, как и длины этих отрезков) называются фокальными радиусами точки
М и обозначаются через r1 и r2 (r1
= F1М, r2= F2М). По определению гиперболы
разность фокальных радиусов ее точки М есть постоянная величина;
эту постоянную принято обозначать через 2а.
Пусть дана какая-нибудь гипербола с фокусами F1 и F2
. Возьмем на плоскости произвольную точку М и обозначим ее
координаты через х и у, а фокальные радиусы F1М
и F2М через r1 и r2.
Точка М будет находиться на (данной) гиперболе в том и только в том
случае, когда
r1— r2= ±2а.
Так как F1 F2=2с и так как фокусы F1
и F2 расположены на оси Ох симметрично относительно
начала координат, то они имеют соответственно координаты (—с; 0) и (+с;
0); приняв это во внимание находим:
Гиперболой называется
геометрическое место точек, для которых разность расстояний от двух
фиксированных точек плоскости, называемых фокусами, есть постоянная величина;
указанная разность берется по абсолютному значению; кроме того,
требуется, чтобы она была меньше расстояния между фокусами и отлична от
нуля. Фокусы гиперболы принято обозначать через F1 и
F2, а расстояние между ними—через 2с.
Пусть М—произвольная точка гиперболы с фокусами F1 и
F2. Отрезки F1М и F2М (так
же, как и длины этих отрезков) называются фокальными радиусами точки
М и обозначаются через r1 и r2 (r1
= F1М, r2= F2М). По определению гиперболы
разность фокальных радиусов ее точки М есть постоянная величина;
эту постоянную принято обозначать через 2а.
Пусть дана какая-нибудь гипербола с фокусами F1 и F2
. Возьмем на плоскости произвольную точку М и обозначим ее
координаты через х и у, а фокальные радиусы F1М
и F2М через r1 и r2.
Точка М будет находиться на (данной) гиперболе в том и только в том
случае, когда
r1— r2= ±2а.
Так как F1 F2=2с и так как фокусы F1
и F2 расположены на оси Ох симметрично относительно
начала координат, то они имеют соответственно координаты (—с; 0) и (+с;
0); приняв это во внимание находим:
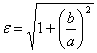 и
и  Параболой называется
геометрическое место точек, для каждой из которых расстояние до некоторой
фиксированной точки плоскости, называемой фокусом, равно расстоянию до
некоторой фиксированной прямой, называемой директрисой (предполагается,
что эта прямая не проходит через фокус).
Фокус параболы принято обозначать буквой F, расстояние от фокуса до
директрисы—буквой p. Величину р называют параметром параболы.
Пусть дана какая-нибудь парабола. Возьмем на плоскости произвольную точку М
и обозначим ее координаты через х и у. Обозначим далее через
r расстояние от точки М до фокуса (r=FM), через d—
расстояние от точки М до директрисы. Точка М будет находиться
на (данной) параболе в том и только в том случае, когда
r=d.
Чтобы получить искомое уравнение, нужно заменить переменные r и d
их выражениями через текущие координаты х, у.
Заметим, что фокус F имеет координаты
Параболой называется
геометрическое место точек, для каждой из которых расстояние до некоторой
фиксированной точки плоскости, называемой фокусом, равно расстоянию до
некоторой фиксированной прямой, называемой директрисой (предполагается,
что эта прямая не проходит через фокус).
Фокус параболы принято обозначать буквой F, расстояние от фокуса до
директрисы—буквой p. Величину р называют параметром параболы.
Пусть дана какая-нибудь парабола. Возьмем на плоскости произвольную точку М
и обозначим ее координаты через х и у. Обозначим далее через
r расстояние от точки М до фокуса (r=FM), через d—
расстояние от точки М до директрисы. Точка М будет находиться
на (данной) параболе в том и только в том случае, когда
r=d.
Чтобы получить искомое уравнение, нужно заменить переменные r и d
их выражениями через текущие координаты х, у.
Заметим, что фокус F имеет координаты 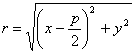 .
Обозначим через Q основание перпендикуляра, опущенного из точки М
на директрису. Очевидно, точка Q имеет координаты
.
Обозначим через Q основание перпендикуляра, опущенного из точки М
на директрису. Очевидно, точка Q имеет координаты 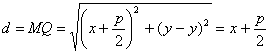
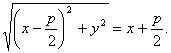 Это и есть уравнение рассматриваемой параболы, так как ему удовлетворяют
координаты точки
М (х; у), когда точка М лежит на данной параболе.
Возведем обе части равенства в квадрат; получим:
Это и есть уравнение рассматриваемой параболы, так как ему удовлетворяют
координаты точки
М (х; у), когда точка М лежит на данной параболе.
Возведем обе части равенства в квадрат; получим:
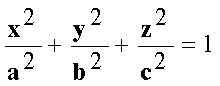 Однополостный гиперболоид
Однополостный гиперболоид
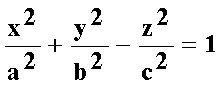 Двухполостный гиперболоид
Двухполостный гиперболоид
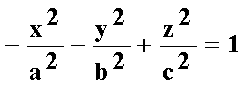 Конус
Конус
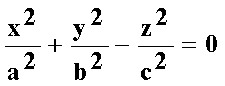 Эллиптический параболоид
Эллиптический параболоид
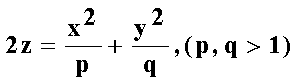 Гиперболический параболоид
Гиперболический параболоид
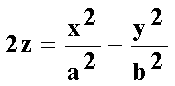 Эллиптический цилиндр
Эллиптический цилиндр
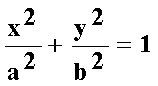 Гиперболический цилиндр
Гиперболический цилиндр
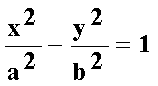 Параболический цилиндр
Параболический цилиндр