|
РУБРИКИ |
Реферат: Математическая модель взаимодействия подсистем производства сельхозпродуктов в районных АПК |
РЕКОМЕНДУЕМ |
||
|
Реферат: Математическая модель взаимодействия подсистем производства сельхозпродуктов в районных АПК/td> | |||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||
|
 |
|
| |||||||
 |
|
| |||||||
|
|
|
| I | Внешние инветиции. |
| aI | Инвестиции, направленные в коллективные хозяйства. (0<a<1) |
| bI | Инвестиции, направленные в частные хозяйства. (0<b<1, a+b=1) |
| X | Валовой продукт. |
| Y | Валовой продукт минус амортизационные отчисления. |
| C | Конечный продукт. |
| П | Природные ресурсы. |
| L | Трудовые ресурсы. |
| A | Амортизационные отчисления. |
| U | Чистые инвестиции (Расширенное воспроизводство). |
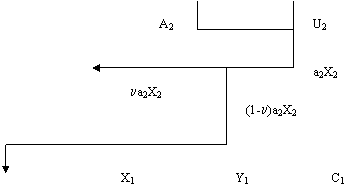
| Доля валового продукта, идущая на капиталовложения. |
(1-n)a2X2 | Доля валового продукта коллективных хозяйств, идущая на инвестиции в частные хозяйства. |
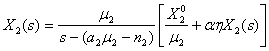 (11)
(11)
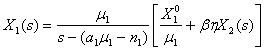 . (12)
Из первого уравнения получим, что конечный продукт сельхозкооператива
выразится следующим образом:
. (12)
Из первого уравнения получим, что конечный продукт сельхозкооператива
выразится следующим образом:
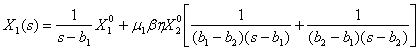 . (17)
Где
. (17)
Где 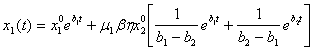 . (18)
При отсутствии внешних инвестиций (I(t)=0) часть валовых капиталовложений
сельхозкооперативов будет отвлекаться на инвестиции в производство частных
хозяйств. Заметим, что эта ситуация более характерна для сложившейся
экономической ситуации, потому что на данный момент инвестиций в
агропромышленный комплекс как таковых нет. Предположим, что коллективное
производство получит капиталовложений
. (18)
При отсутствии внешних инвестиций (I(t)=0) часть валовых капиталовложений
сельхозкооперативов будет отвлекаться на инвестиции в производство частных
хозяйств. Заметим, что эта ситуация более характерна для сложившейся
экономической ситуации, потому что на данный момент инвестиций в
агропромышленный комплекс как таковых нет. Предположим, что коллективное
производство получит капиталовложений 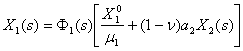 ,
, 6.1. Структурная схема
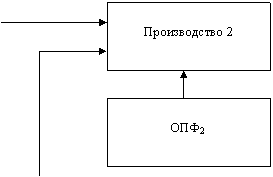
В разделе 5 были получены условия обеспечения расширенного воспроизводства при совместном функционировании сельхозпредприятий и личных хозяйств работников этих предприятий. Рассмотрим далее, каким образом можно повысить эффективность этого взаимодействия. Далее проанализирована модель, в которой личные хозяйства максимизируют свою прибыль за счет перераспределения доли труда, вложенного в предприятия и в личные хозяйства и эта доля зависит от коэффициента k, характеризующий поощрение личных хозяйств за труд, вложенный в сельхозпредприятие. Руководитель предприятия, зная подход личных хозяйств к распределению труда оптимизирует прибыль сельхозпредприятия за счет выбора значения коэффициента поощрения. Как следует из приведенного анализа производства сельхозкооперативов в районных АПК Тверской области, вклад в производство фермерских и подсобных хозяйств незначителен. Соответственно, структура рассматриваемой системы производителей сельхозпродукции может быть представлена в виде двух взаимодействующих подсистем сельхозпредприятий с различными формами собственности и личных хозяйств членов этих кооперативов (Рис. 6.1).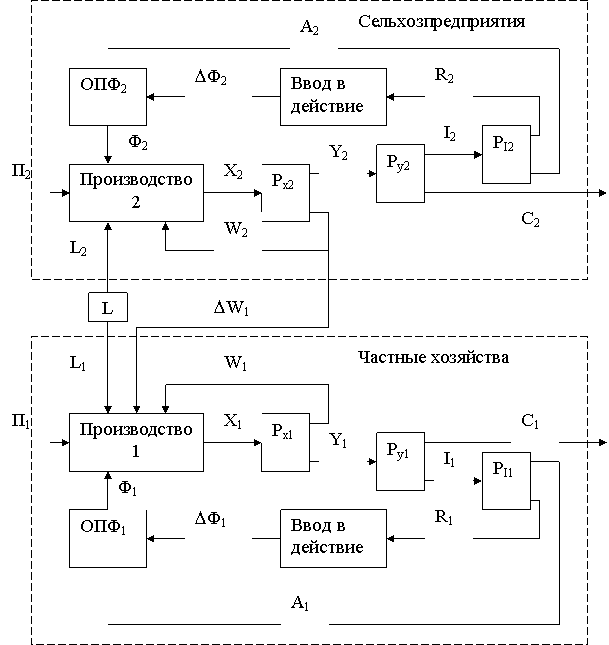
| Где | |
| L | Труд, |
| П | Природные ресурсы, |
| Ф | Основные производственные фонды (ОПФ), |
| X | Валовой продукт, |
| W | Производственное потребление, |
| Y | Конечный продукт, |
| I | Валовые капитальные вложения, |
| C | Непроизводственное потребление, |
| А | Амортизационные отчисления, |
| R | Чистые капитальные вложения. |
6.2. Производственные взаимосвязи.
Для дальнейших рассуждений введем производственную функцию. Валовой продукт агропромышленного предприятия в общепринятом понимании является функцией четырех параметров: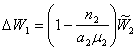 . (19)
Тогда kmax может быть получено преобразованием выражения (18) с
использованием (19):
. (19)
Тогда kmax может быть получено преобразованием выражения (18) с
использованием (19):
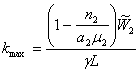 или
или 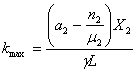 . (20)
С другой стороны, можно действовать следующим образом. Предположим, что
предприятие не получает никакой прибыли, однако оно должно покрыть
амортизацию оборудования и заплатить зарплату своим работникам, для чего
необходимо выполнение следующего неравенства:
. (20)
С другой стороны, можно действовать следующим образом. Предположим, что
предприятие не получает никакой прибыли, однако оно должно покрыть
амортизацию оборудования и заплатить зарплату своим работникам, для чего
необходимо выполнение следующего неравенства:
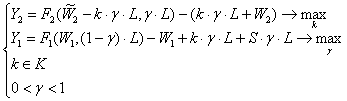 (28)
Рассмотрим второе соотношение. Для достижения максимума необходимо, чтобы
(28)
Рассмотрим второе соотношение. Для достижения максимума необходимо, чтобы 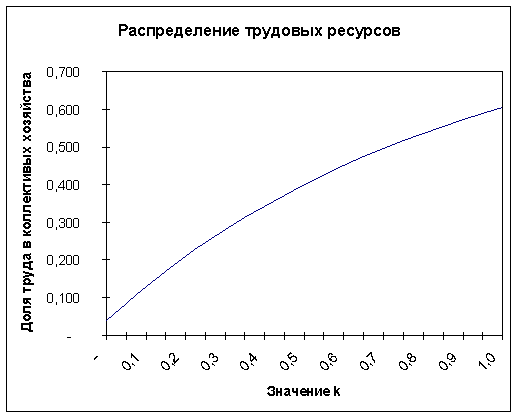 рис. 6.3.1.
Видно, что построенный график удовлетворяет вышеперечисленным условиям.
Производственная функция сельхозкооператива имеет вид:
рис. 6.3.1.
Видно, что построенный график удовлетворяет вышеперечисленным условиям.
Производственная функция сельхозкооператива имеет вид:
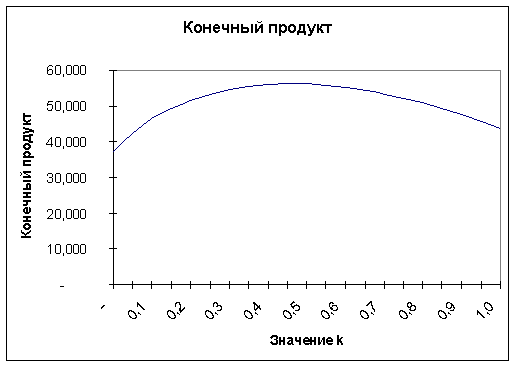 Рис. 6.3.2
К сожалению, аналитически выразить k* не представляется возможным,
однако, используя численные методы, его можно найти. В данном случае оно равно
примерно 0,63. Таким образом, администрация коллективного хозяйства должна
выбрать соответствующий коэффициент поощрения k, основываясь на показателях
своего производства и на отличительных его особенностях.
Вернемся к задаче (31). Напомню, что она характеризует действия дирекции,
направленные не просто на увеличение прибыли своего хозяйства, но и на
увеличении прибыли частных хозяйств. В данном случае вместо g в функции Y1
и Y2 нужно подставить g=Y(k). Задача примет следующий вид:
Рис. 6.3.2
К сожалению, аналитически выразить k* не представляется возможным,
однако, используя численные методы, его можно найти. В данном случае оно равно
примерно 0,63. Таким образом, администрация коллективного хозяйства должна
выбрать соответствующий коэффициент поощрения k, основываясь на показателях
своего производства и на отличительных его особенностях.
Вернемся к задаче (31). Напомню, что она характеризует действия дирекции,
направленные не просто на увеличение прибыли своего хозяйства, но и на
увеличении прибыли частных хозяйств. В данном случае вместо g в функции Y1
и Y2 нужно подставить g=Y(k). Задача примет следующий вид:
7. Заключение.
В работе рассмотрена структура системы производства сельхозпродукции, сложившаяся в настоящее время в районных АПК Тверской области. Из результатов рассмотрения следуют выводы. 1. Из анализа статистичестких данных функционирования районных АПК, можно утверждать, что основными производителями сельхозпродукции в России сейчас являются сельхозпредприятия с различными формами собственности и частные хозяйства работников этих предприятий. Причем наблюдается взаимная интеграция этих производств, связанная с оттоком финансовых средств из первых во вторые. При дальнейшем сохранении сложившегося взаимодействия, существует угроза полного развала этого сектора экономики и экономики страны в целом. 2. Проведен анализ функционирования и взаимодействия подсистем частных и коллективных хозяйств. Разработана математическая модель, позволяющая для определенных условий находить оптимальное решение задачи, при котором сельхозкооперативы оптимизируют прибыль не препятствуя функционированию личных хозяйств. Для этого предложена схема, на основе которой предоставление материальных ресурсов (помощи) частным хозяйствам зависит от труда, вложенного в производство сельхозпредприятий. Основная идея состоит в том, что при определенном характере (количественном значении) помощи личным хозяйствам со стороны сельхозпредприятий, работникам оказывается выгодным выделять для работы на предприятиях необходимую для последних часть своего труда. 3. Для конкретного примера произведены расчеты по оптимизации конечного продукта и проанализирован вид полученных зависимостей. Основная идея решения состояла в том, чтобы ввести в зависимость выделение помощи от количества труда, вложенного в кооператив. Исходя из этого, предположительно можно добиться того, чтобы членам кооператива было выгоднее в нем работать, что решит проблему в целом.8. Литература
1. Каданер Э.Д. Динамическое моделирование экономических систем. Пермь, 1990. 2. Ждакаев С. Конец диктатуры ленивых. // Известия, 17.02.98. 3. Лисичкин Г. Бывшие «братья» в поисках выхода из аграрного тупика. // Известия, 10.08.97. 4. Пугачев В.Ф., Пителин А.К. Анализ вариантов антиинфляционной экономической политики экономике // Экономика и математические методы, 1996’1. 5. Пугачев В.Ф., Пителин А.К. Инфляция в технически отсталой монополизированной экономике // Экономика и математические методы, 1995’1. 6. Основы теории оптимального управления. Под ред. Кротова. Москва, 1990. 7. Моисеев Н. Н. Математические задачи системного анализа. Москва «Наука», 1981. 8. Хромов Ю.С. Производственная безопасность России: внутренние и международные аспекты // Общество и экономика, 1994’9-10. 9. Дроздов Н.Д. Введение в прикладное математическое моделирование. Методология и логика прикладной математики. Тверь, ТвГУ, 1994. 10. Статистические данные хозяйствования Максатихинского и Конаков ского районов в 1992-96 гг. 11. Вахина Н.Д. “Анализ состояния и перспектив развития Максатихинского района”. Дипломная работа. Научный руководитель Дроздов Н.Д., Тверское заочное отделение Северо-западной академии государственной службы. Тверь 1997 г. 12. Рассказова В.Н. “Анализ состояния и перспектив развития Конаковского района”. Дипломная работа. Научный руководитель Дроздов Н.Д., Тверское заочное отделение Северо-западной академии государственной службы. Тверь 1997 г.Страницы: 1, 2
|
|
© 2010 |
|