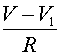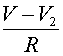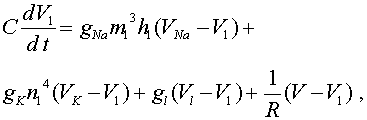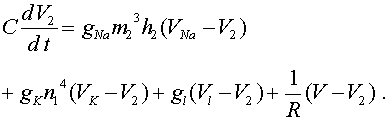|
РУБРИКИ |
Реферат: Математические модели естествознания |
РЕКОМЕНДУЕМ |
||
|
Реферат: Математические модели естествознаниявеличины мембранного потенциала) открываются активационные так называемые -ворота для натриевых каналов. Чем сильнее деполяризована мембрана, тем больше -ворот открыто, что в свою очередь увеличивает деполяризацию. Процесс открытия ворот протекает лавинообразно. При относительно длительной деполяризации натриевые каналы инактивируются. Срабатывают так называемые -ворота, которые блокируют каналы через время порядка 1 мсек после открытия -ворот. В 1980 г. Ф. Сигворс и Э. Неер зарегистрировали токи через единичные натриевые каналы. Оказалось, что они подчиняются закону «все или ничего», Открываются практически мгновенно, а через время около 1 мсек. так же практически мгновенно закрываются. Ионные каналы представляют собой молекулы белка, вкрапленные в липидный слой мембраны. В районы максимума пика потенциала действия большинство натриевых каналов инактивируется, т.е. закрываются -ворота. Встает вопрос: каким образом мембранный потенциал возвращается к исходному уровню -состоянию покоя? Экспериментально А. Ходжкин и А. Хаксли обнаружили, что с некоторым запаздыванием по отношению к началу натриевого тока возникает калиевый ток. Ионы калия начинают покидать клетку, поскольку активируются калиевые каналы. Гипотеза связывает это с открытием так называемых -ворот. Ионы калия движутся в область с меньшей концентрацией (пассивный транспорт). При этом в районе овершута (мембранный потенциал положителен) движение осуществляется в соответствии с направлением электрического поля. Калиевый ток уносит из клетки (точнее с внутренней поверхности мембраны) отрицательный заряд. Мембрана снова поляризуется. Считается, что в отличие от натриевых каналов, для калиевых каналов нет инактивационных ворот. Активационные -ворота сами закрываются, когда мембрана возвращается к уровню потенциала покоя (реполяризуется). Важна отметить, что количество ионов, которое проходит через мембрану при одиночном потенциале действия, практически не вызывает изменения внутриклеточных концентраций ионов. Исключение могут составлять лишь мельчайшие нервные клетки. По некоторым оценкам при одном потенциале действия содержание внутри гигантского аксона кальмара изменяется всего лишь на от исходного. Если блокировать активные натриевые насосы каким-нибудь ядом, то аксон все равно сможет сгенерировать несколько тысяч импульсов. Непосредственно активный транспорт не участвует в генерации спайков. Однако, он поддерживает на должном уровне концентрационные градиенты, наличие которых приводит к возникновению потенциалов действия. После описания механизма генерации спайка, обратимся к системе уравнений, описывающей это процесс. Она предложена А. Ходжкиным и А. Хаксли. Аксон Ходжкина - Хаксли Модель базируется на электрохимическом уравнении (3). Мембранный потенциал будем отсчитывать от его уровня в состоянии покоя, т.е. положим , или же Аналогично введем обозначения для отсчитываемых от равновесных электрохимических потенциалов и сохраняются разности: и мембранного потенциала кроме ионов и и другие ионы, в частности, ионы . Обозначим их суммарный электрохимический потенциал через , соответственно В уравнение (3) для баланса мембранных токов следует добавить слагаемое . Данный ток называется током утечки. Для гигантского аксона кальмара А. Ходжкиным и А. Хаксли были экспериментально найдены значения: мв, мв. Электрохимическое уравнение (3) суть обыкновенное дифференциальное уравнение первого порядка. Как показано выше, его коэффициенты следует считать функциями от мембранного потенциала . По биологическому смыслу решения уравнения ограничены на положительной полуоси . Можно доказать, что все решения такого уравнения монотонно стремятся к состояниям равновесия. Объяснить в рамках одного электрохимического уравнения генерацию потенциала действия невозможно. Из приведенных выше построений следует, проводимости и функциями не только мембранного потенциала , но и времени. Нижеследующие построения А. Ходжкина и А. Хаксли во многом носят феноменологический характер, т.е. не имеют под собой прочной теоретической основы и опираются на ряд допущений и догадок. Рассмотрим натриевую проводимость. Для описания ее зависимости от времени и мембранного потенциала А. Ходжкин и А. Хаксли ввели две новые переменные и характеризуют процессы активации и инактивации натриевых каналов. В интерпретации авторов -вероятность открытия -ворот, -вероятность закрытия -ворот, или же -отношение числа открытых и закрытых ворот соответствующего типа к числу каналов на поверхности мембраны единичной площади. Авторы модели положили: коэффициент назван максимальной натриевой проводимостью. Предложенное А. Ходжкиным и А. Хаксли обоснование вида зависимости в настоящее время выглядит искусственным. Методом подбора были выписаны линейные обыкновенные уравнения первого порядка для переменных . При этом в уравнение для не входит переменная , а в уравнение для не входит Коэффициенты уравнений зависят только от мембранного потенциала . Более менее убедительное обоснование необходимости именно такой зависимости отсутствует. Для описания изменения калиевой проводимости А. Ходжкиным и А. Хаксли была введена функция . Она интерпретировалась как вероятность открытия -ворот для калиевых каналов, т.е. как вероятность активации последних. Напомним, что по гипотезе А. Ходжкина и А. Хаксли инактивационные ворота для калиевых каналов отсутствуют. Авторы опытным путем подобрали линейное обыкновенное дифференциальное уравнение для и положили Коэффициенты уравнения зависят только от мембранного потенциала . Коэффициент называется максимальной калиевой проводимостью. Относительно проводимости для тока утечки А. Ходжкин и А. Хаксли предложили считать его постоянным: . В результате для описания процесса генерации потенциала действия была предложена система четырех уравнений, Первое из них -электрохимическое уравнение для баланса мембранных токов : . Напомним, что Второе и третье уравнения описывают соответственно процессы открытия и закрытия для натриевых каналов. Наконец, четвертое уравнение отражает процесс открытия -ворот для калиевых каналов. Система уравнений Ходжкина -Хаксли имеет следующий вид: , (6) где, напомним, , функции , , положительны и непрерывны. Функции , относятся к классу так называемых сигмоидных функций, т.е. они монотонны обладают следующими свойствами: , при , при Ходжкина и А. Хаксли указан их конкретный вид. Функции весьма сложно устроены. Реально система уравнений допускает только численное исследование. Ограничимся рядом замечаний на качественном уровне, иллюстрирующих впечатления от численного исследования. Входящие в систему (6) -(9) функции подобраны так, что выполнен ряд свойств. Она имеет устойчивое состояние равновесия , где -положительны. Пусть , , не слишком велико, то в силу устойчивости состояния равновесия с течением времени Существует такое пороговое значение , что при системы ведут себя по другому. Первоначально убывает. Однако начинает расти величина . Слагаемое уравнении (6) положительно, т.к. , а В результате производная V¢(t) становится положительной. Мембранный потенциал начинает расти (момент начала генерации спайка). Вместе с ним растет и величина , что приводит к дальнейшему увеличению V¢(t) и ускорению роста . Однако, чуть позже начинает уменьшаться величина . Это замедляет рост , тем более, что уменьшается разность . Одновременно растет величина . Соответствующее слагаемое в уравнении (6) отрицательно, т.к. и момент времени где V¢(tm)=0. Это точка максимума потенциала действия. Значение мембранного потенциала относительно близко к . После прохождения точки максимума значение производной V¢(t) определяется значением слагаемого и становится отрицательным. Скорость убывания мембранного потенциала на нисходящем участке спайка меньше по абсолютной величине, чем скорость роста на восходящем участке. Нисходящий участок продолжительнее восходящего. В дальнейшем значение становится отрицательным, а после этого . Величины , своим равновесным значениям. Процесс генерации спайка закончен. Особо подчеркнем значимость факта, что система (6) -(7) обладает пороговыми свойствами. Существует такое критическое значение мембранного потенциала, что при начальном отклонении мембранного потенциала с течением времени значение . Если же некоторое время (его называют скрытым, или латентным периодом) генерируется спайк. Модель адекватно отражает пороговые свойства реального аксона. Если воздействовать на мембрану кратковременным толчком деполяризующего тока (отклоняющего мембранный потенциал в положительном направлении), то после слабого воздействия мембранный потенциал возвращается в равновесное состояние. Вследствие достаточно сильного воздействия спустя латентный период генерируется спайк. Обсудим еще одно свойство аксона. Гигантские аксоны достигают длины нескольких десятков сантиметров. Мембранный потенциал на разных участках аксона может различаться. Аксон представляет собой так называемую распределенную систему. Если подействовать на некоторый участок аксона допороговым деполяризующим толчком тока, то мембранный потенциал на этом и некотором примыкающем к нему участке отклонится от равновесного состояния в положительном направлении. Такое отклонение называется локальным ответом. Возмущение с течением времени затухает, одновременно, как капля, растекаясь по аксону. В результате локальные ответы, возникшие при стимулировании различных участков, могут накладываться друг на друга, т.е., как говорят, суммироваться по пространству. Если же на участок аксона повторно подается деполяризирующий ток, то новый локальный ответ накладывается на предыдущий. Говорят, что происходит временное суммирование. Локальные ответы градуальны. Их амплитуда зависит от силы стимула (точнее, силы -длительности). В случае, когда локальный ответ в результате суммации, или же после достаточно сильного одноразового локального воздействия достигает порогового уровня, запускаются механизмы генерации потенциала действия. Зародившись локально, потенциал действия распространяется по аксону. Явление распространения объясняется следующим образом. Цитоплазма - электролит, а, следовательно, хороший проводник. Если между точками существуют ненулевые разности потенциалов, то вдоль мембраны возникают токи (вблизи поверхности). Они направлены от точек с более высоким потенциалом к точкам, где он меньше, и подчиняются закону Ома. Вследствие этого потенциал на участках, прилегающих, к области генерации спайка, растет и достигает порогового значения. В результате эти участки сами генерируют потенциалы действия. Процесс распространяется вдоль аксона. Проведение нервных импульсов обладает важной особенностью. При “столкновении” они аннигилируют, т.е. уничтожаются. С помощью локального воздействия возбудим аксон в двух точках. По нему будут распространяться четыре импульса, два из которых движутся во встречных направлениях. Данные импульсы встретятся и не пропустят друг друга. Это связано с тем, что мембрана обладает следующим свойством. Во время потенциала действия и некоторое время после его завершения она не реагирует на воздействие. В частности, после завершения спайка некоторое время не способна сгенерировать нового потенциала действия. Данное состояние называется абсолютной рефрактерностью. Отметим, что постепенно абсолютная рефрактерность сменяется относительной. Для того, чтобы инициировать потенциал действия в состоянии относительной рефрактерности, нужно применить более мощный стимул, нежели в состоянии покоя. Для описания процесса распространения потенциала действия вдоль аксона А. Ходжкин и А. Хаксли модернизировали уравнение (6). Пусть -координата точки вдоль аксона, а -значение мембранного потенциала в этой точке. Используется закон Ома, согласно которому ток через сечение пропорционален градиенту напряжения (в одномерном случае -производной). Ток через сечение равен направление выбрано в сторону возрастания , коэффициент -проводимость. Выделим участок аксона, координаты точек которого заключены в интервале Суммарный ток через сечения и . Используя формулу Лагранжа получим: , где поверхность мембраны выбранного участка аксона проходят емкостной , натриевый калиевый также ток утечки Пусть мембранный ток приближенно равен . Привлекая закон Кирхгофа, получим: . Используя приведенные ранее формулы (4), (5) для мембранных токов и устремляя к нулю, приходим к уравнению: Его часто называют уравнением аксона Ходжкина -Хаксли. В (10) функции , как и выше подчиняются уравнениям (7) -(9). А. Ходжкин и А. Хаксли исследовали так называемые автоволновые решения системы уравнений, т. е. решения типа бегущих волн: (аналогично для , -скорость распространения волны. После подстановки в (11) для получается обыкновенное дифференциальное уравнение: Система (7) -(9), (11) исследовалась численно. Методом подбора было найдено значение скорости при которой система уравнений имела приемлемое по мнению авторов решение. Параметры полученного при исследовании системы уравнений распространяющегося потенциала действия оказались близкими к реально наблюдаемым в эксперименте. Скорость распространения импульса по гигантскому аксону относительно не велика (по сравнению с аналогичными по назначению проводниками нервных импульсов у человека). Она растет с увеличением диаметра аксона. Увеличение диаметров аксонов избрала природа для высокоскоростного проведения импульсов у беспозвоночных. Однако, когда организму нужна не только быстрота реакции, но и огромное количество связей, гигантские аксона становятся не приемлемыми. Например, в зрительном нерве, где больше миллиона связей, для больших аксонов не хватило бы места. Длинные аксоны у человека и позвоночных животных покрыты достаточно толстым липидным слоем -миелиновой оболочкой (точнее, они обвиты клетками содержащими и вырабатывающими миелин). В миелиновой оболочке присутствуют регулярно расположенные разрывы, где мембрана аксона оголена. Разрывы называются перехватами Ранвье. Миелинизированные участки имеют длину порядка 1 -2 мм. Протяженность перехватов Ранвье около 1 мкм. Перехваты Ранвье способны генерировать спайки. Миелинизированные участки обладают емкостью и омическим сопротивлением, но они не генерируют спайков. Импульсы по миелинизированным участкам распространяются пассивно, т.е. с затратами энергии на омическое сопротивление и на перезаряд участка, представляющего собой конденсатор (обратимые потери). Суммарно затраты энергии не велики. Рассмотрим миелинизированный участок, ограниченный двумя перехватами. Пусть левый перехват генерирует спайк. Возмущение (положительное) по миелинизированному участку передается правому перехвату. Когда отклонение мембранного потенциала правого участка достигает порогового значения, он генерирует спайк. Этот импульс не может вызвать генерацию нового спайка левым перехватом Ранвье, поскольку тот находится в рефрактерном состоянии (в состоянии невосприимчивости). Однако, данный перехват по той же схеме возбуждает перехват, следующий за ним справа. По миелинизированному аксону, перескакивая от перехвата к перехвату, будет распространяться импульс. Процесс называется сальтаторным проведением возбуждения (saltare - прыгать). Оно обеспечивает скорость распространения импульсов в 20- 25 раз более высокую, чем в гигантских аксонах того же диаметра. Описанный процесс сальтаторного проведения импульсов легко формализуется. В простейшем случае это выглядит следующим образом. Пусть и потенциалы левого и правого перехватов Ранвье, а -потенциал миелинизированного участка (считаем его во всех точках участка одинаковым). Тогда между участком и соответствующими перехватами проходят токи: и -сопротивление перехода от перехвата к миелинизированному участку. Через миелиновую оболочку проходят емкостной ток V¢ и ток утечки , где емкость, а суммарное сопротивление миелиновой оболочки. В силу первого закона Кирхгофа получаем: Для описания мембранных потенциалов и уравнение (6), в правую часть которого согласно закону Кирхгофа следует добавить для левого перехвата слагаемое , а для правого -слагаемое . Это токи, проходящие между соответствующими перехватами и миелинизированным участком. В результате получим уравнения: Величины и удовлетворяют уравнениям (7) -(9), в которых для левого и правого перехватов следует положить соответственно. Ключевые источники естествознания Имея в виду рациональность перехода от натурфилософии к математически точному естествознанию, В.И. Вернадский отмечал одинаковую существенность и взаимную дополнительность двух основных и воистину универсальных математических методов - количественного (арифметического или алгебраического) и качественного (геометрического), т. е. интегрального (внешнего) и дифференциального (внутреннего): «Одно и то же природное явление может быть независимо охвачено обоими этими направлениями творческой математической мысли». Отдавая должное философии и сознавая «огромное значение математики для естествознания», он все-таки полагал, что «в основе естествознания лежат только научные эмпирические факты и научные эмпирические обобщения»: «Все основные научные эмпирические понятия при логическом анализе приводят к иррациональному остатку...Никогда ни одно научно изучаемое явление, ни один научный эмпирический факт и ни одно научное эмпирическое обобщение не может быть выражено до конца, без остатка, в словесных образах, в логических построениях - в понятиях - в тех формах, в пределах которых только и идет работа философской мысли, их синтезирующая, их анализирующая. В предметах исследования науки всегда остается неразлагаемый рационалистически остаток, иногда большой, который влияет на эмпирическое научное изучение, остаток, исчезающий нацело из идеальных построений философии, космогонии или математики и математической физики. Глубокая мысль, в яркой красивой форме выраженная Ф. И. Тютчевым- «Мысль изреченная есть ложь», всегда сознательно или бессознательно чувствуется испытателем природы и всяким научным исследователем, когда он в своей научной работе сталкивается с противоречиями между эмпирическими научными обобщениями и отвлеченными построениями философии или когда факты заставляют его менять и уточнять (обычно осложнять, а часто резко упрощать) свои гипотезы, особенно часто - неизбежно ограниченные математические выражения природных явлений». Поэтому Вернадский считал необходимым исходить прежде всего или, в конечном счете, именно из ключевых научных эмпирических фактов или соответствующих ключевых научных эмпирических обобщений (типа открытой Менделеевым Периодической системы химических элементов—«одного из величайших эмпирических обобщений»), т. е. обращаться непосредственно к этим естественным ключевым источникам, как бы вспоминая красноречивое тютчевское «Молчание»: Как сердцу высказать себя? Другому как понять тебя? Поймет ли он, чем ты живешь? Мысль изреченная есть ложь. Взрывая, возмутишь ключи, Питайся ими—и молчи. Всегда остающийся в предметах исследования науки неразлагаемый рационалистически остаток, т. е. иррациональный остаток, к которому приводят все основные научные эмпирические понятия при логическом анализе, означает, что мы должны принимать во внимание наряду с безусловно необходимыми - достоверными - фактами, характерными для вполне детерминистической классической механики, и факты вероятностные, лежащие в основе надлежащей квантовой механики (с ее соответствующей вероятностной интерпретацией и с характерным для нее принципом неопределенности), а также факты веры, с которыми имеют дело не только все религии, но и атеизм, поскольку «основанные на философских заключениях» «атеистические представления,—как справедливо заметил Вернадский, - по существу тоже предмет веры». Чуть ли не все подвергая сомнению, Вернадский замечает: «Но это не касается эмпирических обобщений, которые в основе своей существенно отличны от научных теорий и научных гипотез, с которыми они обычно смешиваются». При этом он считал принципиально необходимым и возможным стремиться к предельно полному охвату природных явлений и самой Природы в целом. Однако в пределе, охватывая в целом Природу, Вселенную, материю (со всеми присущими ей атрибутами, вплоть до Жизни и Разума, в том числе Высшего Разума - с бесконечными потенциальными возможностями), мы по крайней мере в принципе можем и должны получить - и действительно получаем! - не только искомое воистину универсальное (предельно полное) ключевое научное эмпирическое обобщение в виде вполне детерминированных взаимосвязанных периодических систем всевозможных (так называемых эталонных и производных) фундаментальных структурных элементов материи на всех четырех возможных последовательных основных уровнях ее естественной самоорганизации - физическом, химическом, биологическом и психологическом (т. е. на самом деле величайшее атомистическое научное эмпирическое обобщение менделеевского типа), но и адекватное ему столь же универсальное ключевое научное теоретическое обобщение в виде совершенно однотипных по своей симметрии и, соответственно, непосредственно однозначно дедуктивно определяемых по надлежащей математической индукции вполне детерминированных взаимосвязанных периодических систем всевозможных равномерно квантованных собственных значений всех возможных универсальных характеристик рассматриваемых элементов. Список используемой литературы 1. Пуанкаре А. «О науке».М., 1983 2. Аристотель «Сочинения». М., «Мысль», 1975 г. 3. Кант И. «Сочинения», М., «Мысль», 1964 г. 4. Н.К.Вахтомин «Теория научного знания Иммануила Канта». М., «Наука», 1986 г. 5. Кедров Б.М. «Предмет и взаимосвязь естественных наук».М., «Наука»,1967.436с. 6. «Природа и общество» М, «Наука,1968.348с. 7. «Физика ХХ века. Развитие и перспективы.» Сборник. М,«Наука,1984.334с. 8. Алексеев И.С., Овчинников Н.Ф., Печенкин А.А. «Методология обоснования квантовой теории». М.: «Наука»,1984.334с. 9. В.И.Кузнецов, Г.М.Идлис, В.Н.Гутина «Естествознание» М, «Агар»,1996,384с. Страницы: 1, 2 |
|
© 2010 |
|
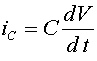 ,
, 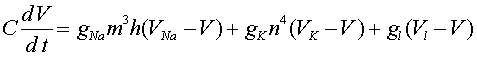
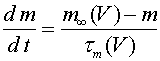 , (7)
, (7)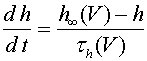 , (8)
, (8)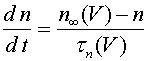 , (9)
, (9)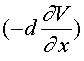 , где
, где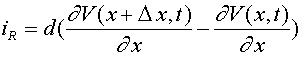
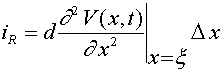
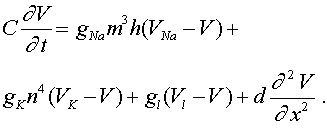 (10)
(10)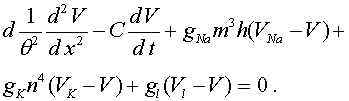 (11)
(11)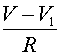
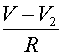 , где
, где 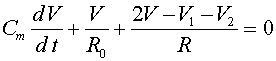 .
.