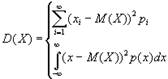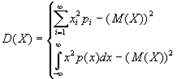|
|
|
|
Реферат: Матожидание, дисперсия, мода и медиана
Реферат: Матожидание, дисперсия, мода и медиана
Математическое ожидание и его свойства.
Одной из важных числовых характеристик случайной величины является
математическое ожидание. Введем понятие системы случайных величин.
Рассмотрим совокупность случайных величин 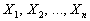 , которые являются результатами одного и того же случайного эксперимента. Если
, которые являются результатами одного и того же случайного эксперимента. Если 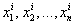 — одно из возможных значений системы
— одно из возможных значений системы 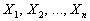 , то событию
, то событию 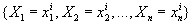 соответствует
определенная вероятность удовлетворяющая аксиомам Колмогорова. Функция соответствует
определенная вероятность удовлетворяющая аксиомам Колмогорова. Функция
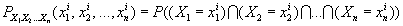 , определенная при любых возможных значениях
, определенная при любых возможных значениях 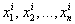 случайных величин
случайных величин 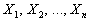 , называется
совместным законом распределения. Эта функция позволяет вычислять
вероятности любых событий из , называется
совместным законом распределения. Эта функция позволяет вычислять
вероятности любых событий из 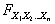 .
В частности, совместный закон распределения случайных величин .
В частности, совместный закон распределения случайных величин 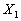 и
и 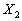 , которые принимают значения
из множества , которые принимают значения
из множества 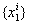 и и 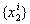 , задается вероятностями
, задается вероятностями 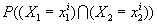 .
Расширим понятие независимости случайных событий и введем понятие независимых
случайных величин.
1) Математическое ожидание постоянной величины равно самой постоянной, т.е. .
Расширим понятие независимости случайных событий и введем понятие независимых
случайных величин.
1) Математическое ожидание постоянной величины равно самой постоянной, т.е. 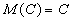 .
Доказательство. Постоянную .
Доказательство. Постоянную 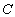 можно рассматривать как дискретную случайную величину, принимающую единственное
значение
можно рассматривать как дискретную случайную величину, принимающую единственное
значение 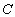 с вероятностью 1. с вероятностью 1. 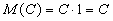 .
2) Постоянный множитель можно выносить за знак математического ожидания:
.
2) Постоянный множитель можно выносить за знак математического ожидания: 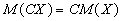 .
Доказательство. Пусть случайная величина .
Доказательство. Пусть случайная величина 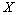 задана законом распределения вероятностей:
Очевидно, что случайная величина
задана законом распределения вероятностей:
Очевидно, что случайная величина 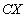 также является дискретной и принимает значения
также является дискретной и принимает значения 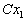 ,
, 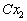 , ... , , ... , 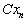 , ... с прежними вероятностями
, ... с прежними вероятностями 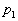 ,
, 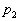 , ... , , ... , 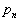 , ... т.е. закон распределения
, ... т.е. закон распределения 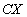 имеет вид
Тогда по определению математического ожидания
имеет вид
Тогда по определению математического ожидания
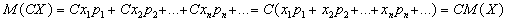 .
3) Математическое ожидание произведения нескольких взаимно независимых
случайных величин равно произведению их математических ожиданий:
.
3) Математическое ожидание произведения нескольких взаимно независимых
случайных величин равно произведению их математических ожиданий:
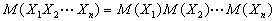 .
Доказательство. Рассмотрим случайную величину .
Доказательство. Рассмотрим случайную величину 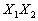 и докажем, что и докажем, что 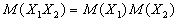 Действительно, если
Действительно, если 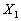 и и 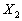 заданы рядами распределения
то, как было указано выше, случайная величина заданы рядами распределения
то, как было указано выше, случайная величина 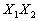 имеет следующий закон распределения:
Тогда
имеет следующий закон распределения:
Тогда
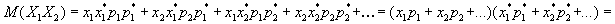
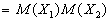 .
Методом математической индукции можно доказать, что если это свойство
выполняется для .
Методом математической индукции можно доказать, что если это свойство
выполняется для 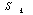 случайных
величин, то оно выполняется и для случайных
величин, то оно выполняется и для 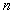 случайных величин.
4) Математическое ожидание суммы нескольких случайных величин равно сумме
математических ожиданий слагаемых:
случайных величин.
4) Математическое ожидание суммы нескольких случайных величин равно сумме
математических ожиданий слагаемых: 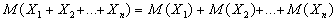 .
Доказательство. Пусть заданы две случайные величины
.
Доказательство. Пусть заданы две случайные величины 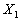 и
и 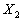 рядами распределения (см.
предыдущее свойство).
В силу вышесказанного возможные значения случайной величины рядами распределения (см.
предыдущее свойство).
В силу вышесказанного возможные значения случайной величины 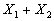 будут
будут 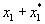 , , 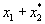 ,
, 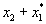 , , 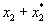 , ... Их вероятности
, ... Их вероятности 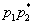 , , 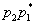 ,
, 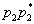 , ... , т.к. они определяются
по теореме умножения вероятностей. Т.к. вероятность , ... , т.к. они определяются
по теореме умножения вероятностей. Т.к. вероятность 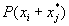 обозначает вероятность того, что события
обозначает вероятность того, что события 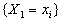 и
и 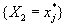 наступают совместно, т.е. наступают совместно, т.е.
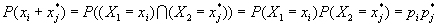 .
Переходя к математическом ожиданию рассматриваемой суммы, имеем
.
Переходя к математическом ожиданию рассматриваемой суммы, имеем
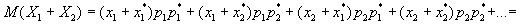
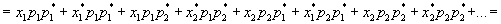
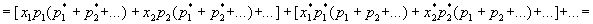
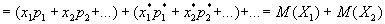 Предположим, что свойство 4) справедливо для
Предположим, что свойство 4) справедливо для 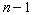 случайной величины применяя в очередной раз метод математической индукции
докажем, что это свойство справедливо и для
случайной величины применяя в очередной раз метод математической индукции
докажем, что это свойство справедливо и для 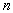 случайных величин.
Дисперсия случайной величины
На практике часто требуется оценить рассеивание возможных значений случайной
величины вокруг ее среднего значения. Отклонением случайной величины
случайных величин.
Дисперсия случайной величины
На практике часто требуется оценить рассеивание возможных значений случайной
величины вокруг ее среднего значения. Отклонением случайной величины 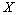 является разность между значением случайной величины и ее математическим
ожиданием и обозначается
является разность между значением случайной величины и ее математическим
ожиданием и обозначается 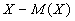 .
Хотя отклонение является величиной случайной, но использовать его для оценки
разброса не удобно, т.к. его математическое ожидание всегда равно 0. Поэтому
для характеристики рассеивания вводят другие характеристики.
Определение. Дисперсией случайной величины называется математическое
ожидание квадрата ее отклонения: .
Хотя отклонение является величиной случайной, но использовать его для оценки
разброса не удобно, т.к. его математическое ожидание всегда равно 0. Поэтому
для характеристики рассеивания вводят другие характеристики.
Определение. Дисперсией случайной величины называется математическое
ожидание квадрата ее отклонения: 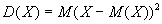 .
Из этого определения следует, что дисперсия случайной величины
.
Из этого определения следует, что дисперсия случайной величины 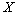 вычисляется по формуле
вычисляется по формуле
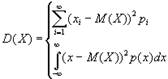
| для дискретной случайной величины 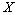 для непрерывной случайной величины 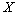 . . | (1) |
Справедлива следующая теорема.
Теорема. Дисперсия случайной величины равна математическому ожиданию
ее квадрата минус квадрат математического ожидания: 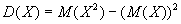 .
Доказательство. Из определения дисперсии и учитывая, что математическое
ожидание — постоянная величина, получим
.
Доказательство. Из определения дисперсии и учитывая, что математическое
ожидание — постоянная величина, получим
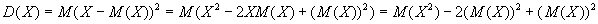 .
Тогда формула (1) примет вид
.
Тогда формула (1) примет вид
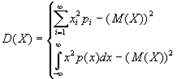
| для дискретной случайной величины 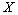 для непрерывной случайной величины 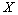 . . | (2) |
Свойства дисперсии
- Дисперсия постоянной величины
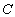 равна нулю: равна нулю: 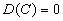 . .
Действительно, 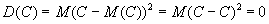 . .
- Постоянный множитель можно выносить за знак дисперсии, возводя его
в квадрат:
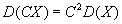 . .
Доказательство. По определению дисперсии и в силу свойств математического
ожидания получаем:
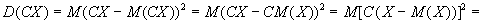
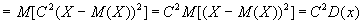 . .
- Дисперсия суммы нескольких независимых случайных величин равна
сумме дисперсий этих величин:
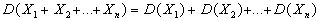 .
Доказательство. Вначале докажем свойство для двух величин .
Доказательство. Вначале докажем свойство для двух величин 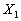 и и 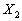 .
По теореме .
По теореме
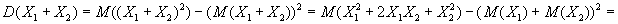
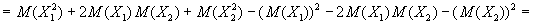
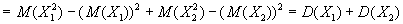 И далее методом математической индукции...
Следствие 1. Дисперсия суммы постоянной величины и случайной величины
И далее методом математической индукции...
Следствие 1. Дисперсия суммы постоянной величины и случайной величины 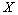 равна дисперсии случайной величины
равна дисперсии случайной величины 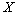 :
: 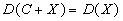 .
Действительно, .
Действительно,  .
Следствие 2. Дисперсия разности двух независимых случайных величин равна
сумме их дисперсий: .
Следствие 2. Дисперсия разности двух независимых случайных величин равна
сумме их дисперсий: 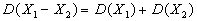 .
Доказательство. Используя свойства 2) и 3), получаем .
Доказательство. Используя свойства 2) и 3), получаем
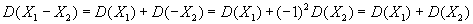 .
Дисперсия случайной величины как характеристика разброса имеет одну неудобную
особенность: ее размерность (из определения) равна квадрату размерности
случайной величины
.
Дисперсия случайной величины как характеристика разброса имеет одну неудобную
особенность: ее размерность (из определения) равна квадрату размерности
случайной величины 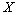 .
Определение. Средним квадратическим отклонением случайной величины .
Определение. Средним квадратическим отклонением случайной величины 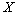 называется арифметический корень из дисперсии, т.е.
называется арифметический корень из дисперсии, т.е. 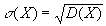 .
Зная введенные две числовые характеристики — математическое ожидание
.
Зная введенные две числовые характеристики — математическое ожидание 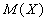 и среднее квадратическое отклонение
и среднее квадратическое отклонение 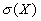 , — получаем ориентировочное представление о пределах возможных значений
случайной величины.
Мода и медиана как разновидность средних величин в вариационных рядах
Средние величины являются своего рода отвлеченной, абстрактной величиной.
Отвлекаясь от конкретных величин каждого варианта, эти числа отражают то
общее, что присуще всей совокупности единиц. При этом может случиться, что
величина средней не имеет равенства ни с одним из конкретных вариантов
встречающихся в рассматриваемой совокупности вариантов.
Например, среднее число членов семьи, равное 3,84, полученное на основе
исчисления соответствующей совокупности данных, ничего общего с конкретным
составом семьи не имеет, поскольку дробного числа членов семьи не может быть.
Здесь в данном показателе средней величины состава семьи выражается некоторое
центральное значение, около которого группируются реально существующие
варианты.
Кроме рассмотренных средних, когда определяется некая абстрактная величина,
могут быть использованы величины конкретных вариантов имеющихся в
рассматриваемой совокупности величин, величин занимающих определенное место в
ранжированном ряду индивидуальных значений признака. Ранжировка признаков
может быть построена в порядке возрастания или убывания индивидуальных
значений признака. Такими величинами, чаще всего являются мода и медиана.
Мода - это наиболее часто встречающаяся в совокупности величина варианта. Эту
величину означают символом Мо.
Мода как величина в дискритном (прерывистом) ряду определяется следующим
образом на примере выявления наибольшего процента мужчин носящих определенный
размер обуви. Наглядно это можно представить следующей таблицей.
Распределение числа мужчин по размеру используемой обуви
, — получаем ориентировочное представление о пределах возможных значений
случайной величины.
Мода и медиана как разновидность средних величин в вариационных рядах
Средние величины являются своего рода отвлеченной, абстрактной величиной.
Отвлекаясь от конкретных величин каждого варианта, эти числа отражают то
общее, что присуще всей совокупности единиц. При этом может случиться, что
величина средней не имеет равенства ни с одним из конкретных вариантов
встречающихся в рассматриваемой совокупности вариантов.
Например, среднее число членов семьи, равное 3,84, полученное на основе
исчисления соответствующей совокупности данных, ничего общего с конкретным
составом семьи не имеет, поскольку дробного числа членов семьи не может быть.
Здесь в данном показателе средней величины состава семьи выражается некоторое
центральное значение, около которого группируются реально существующие
варианты.
Кроме рассмотренных средних, когда определяется некая абстрактная величина,
могут быть использованы величины конкретных вариантов имеющихся в
рассматриваемой совокупности величин, величин занимающих определенное место в
ранжированном ряду индивидуальных значений признака. Ранжировка признаков
может быть построена в порядке возрастания или убывания индивидуальных
значений признака. Такими величинами, чаще всего являются мода и медиана.
Мода - это наиболее часто встречающаяся в совокупности величина варианта. Эту
величину означают символом Мо.
Мода как величина в дискритном (прерывистом) ряду определяется следующим
образом на примере выявления наибольшего процента мужчин носящих определенный
размер обуви. Наглядно это можно представить следующей таблицей.
Распределение числа мужчин по размеру используемой обуви
Размер обуви | Число мужчин старше 16 лет % к итогу | Накопление частности | | До 37 | 1 | 1 | | 38 | 5 | 6 | | 39 | 12 | 18 | | 40 | 23 | 41 | | 41 | 28 | 69 | | 42 | 21 | 90 | | 43 | 8 | 98 | | 44 | 2 | 100 | | и более | - | | Всего | 100 | |
В распределении мужчин по размеру обуви наибольшая часть мужчин (28%)
относится к величине номера обуви в 41. Следовательно, мода Мо = 41, т.е.
модой является 41-й размер обуви.
Чтобы определить медиану, необходимо найти один из центральных вариантов
рассматриваемой совокупности. В нашем примере центральным вариантом будет
находиться в центре совокупности состоящей из 100 членов, т.е. 100 : 2 = 50.
Затем по накопленным частотам определяем величину 50-го члена ряда. В нашем
примере он будет находиться между 41 и 69 накопленной частности (см. 3-ий
столбец таблицы), 50-ый член ряда имеет величину 41, т.е. Ме = 41-му размеру
обуви.
В практике мода и медиана часто используются вместо средней арифметической
или наряду с ней. Так, фиксируя средние цены на оптовых рынках, записывают
наиболее часто встречающуюся цену каждого продукта, т.е. определяют моду
цены. Тем не менее наилучшей характеристикой величины варианта служит средняя
арифметическая, которая имеет ряд существенных преимуществ, о которых было
сказано раньше, главное из которых, точное отражение суммы всех значений
признака, использующихся для решения соответствующих практических задач.
|
|
|
|
|