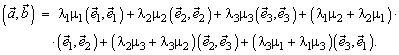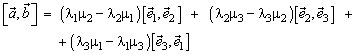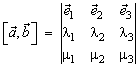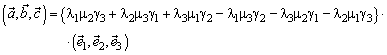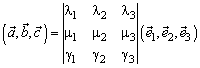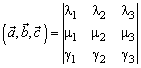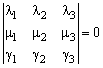|
РУБРИКИ |
Реферат: Векторы. Действия над векторами |
РЕКОМЕНДУЕМ |
||
|
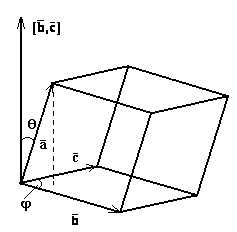
Реферат: Векторы. Действия над векторамивектором базиса φ, тогда . Пример: Пусть вектор единичной длины векторами и пространстве углы α, β, γ, соответственно (рис.11), тогда . Причем cosβ, cosγ называются направляющими косинусами вектора Глава 6. Скалярное произведение Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если один из векторов нулевой скалярное произведение считается равным нулю. Скалярное произведение векторов и [или ]. Если φ - угол между векторами и . Скалярное произведение обладает следующими свойствами: 1. 2. 3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них нулевой. 4. 5. 6. Теорема: В ортогональном базисе Действительно, пусть каждое слагаемое коллинеарно соответствующему базисному вектору. Из теоремы второго раздела следует, что где выбирается знак плюс или минус в зависимости от того, одинаково или противоположно направлены векторы , и , где φ - угол между векторами , и . Аналогично вычисляются и остальные компоненты. Скалярное произведение используется для решения следующих основных задач: 1. Пусть в некотором базисе векторы тогда, пользуясь свойствами скалярного произведения, можно записать: Величины Теорема: В ортонормированном базисе Замечание: Все рассуждения этого раздела приведены для случая расположения векторов в пространстве. Случай расположения векторов на плоскости получается изъятием лишних компонент. Автор предлагает сделать вам это самостоятельно. Глава 7. Векторное произведение
Упорядоченная тройка некомпланарных векторов называется правоориентированной (правой), если после приложения к общему началу из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. В противном случае упорядоченная тройка некомпланарных векторов называется левоориентированной ( левой). Определение: Векторным произведением вектора на вектор , удовлетворяющий условиям: 1. 2. вектор 3. упорядоченная тройка векторов Если один из векторов нулевой, то векторное произведение есть нулевой вектор. Векторное произведение вектора Теорема: Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения. Теорема: Длина (модуль) векторного произведения двух векторов равняется площади параллелограмма, построенного на этих векторах как на сторонах. Пример: Если Пример: Если Пример: Пусть, ортогонален к получается из вектора вокруг вектора по часовой стрелке (если смотреть из конца вектора ). Пример: Если дан вектор , то каждый вектор можно представить в виде суммы , где , а . Легко видеть, что Действительно, можно заметить, что . Вектор и и (рис. 12), что они одинаково направлены. Векторное произведение обладает следующими свойствами: 1. Действительно, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей. Точно так же вектор коллинеарен вектору переставляя сомножители, мы должны изменить направление произведения, чтобы было выполнено условие 3) определения. Действительно, если , - правая тройка, то , , - снова правая тройка. 2. Если φ - угол между векторами и . Векторы, стоящие в обеих частях доказываемого равенства, лежат на прямой, перпендикулярной . При λ > 0 и вектор вектор направлены так же, как Если λ < 0, то кратчайший поворот от к кратчайшему повороту от . Поэтому противоположно направлены. Очевидно, что противоположно направлены также и векторы . Таким образом, при λ ≠ 0 векторы и и равенство доказано. При λ = 0 равенство очевидно. 3. Если очевидно. Если и и и , а коллинеарны , и вектор , а , нам достаточно доказать равенство и (в силу свойства 2) даже равенство , где равна 1. Выше, в примере, мы видели, что в этом случае умножение на сводится к повороту (ортогонального к ) первого сомножителя на угол 90°. Но при повороте параллелограмм, построенный на , поворачивается целиком вместе с диагональю. Тем самым равенство доказано. 4. Пусть в некотором базисе или Теорема: В ортонормированном базисе или {если базис левый, то перед одной из частей каждого равенства следует поставить знак минус}. Справедливость теоремы следует из предыдущих формул при учете примеров в начале раздела. Чтобы избежать постоянных замечаний об ориентации базиса, мы будем считать, что базис выбирается всегда правый. Векторное произведение используется в основном для решения двух задач: 1. Нахождения вектора перпендикулярного плоскости, в которой расположены два заданных вектора. 2. Вычисление площади S параллелограмма, построенного на векторах и ортонормированном базисе В планиметрии векторное произведение не определено. Но ничто не мешает считать, что изучаемая плоскость помещена в пространство и третий базисный вектор выбран единичным и перпендикулярным плоскости. Тогда векторное произведение имеет одну ненулевую компоненту, а именно третью, и площадь параллелограмма в ортонормированном базисе на плоскости выражается формулой Глава 8. Смешанное произведение Определение: число Смешанное произведение векторов Теорема: Смешанное произведение трех векторов равно объему параллелепипеда, построенного на векторах как на ребрах, взятому со знаком плюс если тройка правая, и со знаком минус, если тройка левая. Действительно, угол между векторами , а θ - угол между векторами и построенного на векторах и произведению площади основания на высоту первое утверждение доказано. Знак смешанного произведения совпадает со знаком cosθ, и поэтому смешанное произведение положительно когда направлен в ту же сторону от плоскости векторов и , т. е. когда тройка , доказывается, что смешанное произведение левой тройки векторов отрицательно. Пример: Если ортонормированный базис, то или это базис или левый. Теорема: Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения. Равенство a.хотя бы один вектор нулевой; тогда все три вектоpaкомпланарны; b.sinφ = 0 тогда c.cosθ = 0 тогда вектор Обратное утверждение доказывается аналогично. Смешанное произведение обладает следующими свойствами: 1. 2. 3. Пусть в некотором базисе или В частности, в ортонормированном базисе {если базис левый, то перед одной из частей равенства следует поставить знак минус}. Следствие: Условие является необходимым и достаточным условием компланарности трех векторов, заданных своими координатами в некотором базисе Глава 9. Двойное векторное произведение Определение: Вектор Теорема: Для любых векторов Литература
Действительно, этим числом является или , или направлены ли векторы одинаково или противоположно. Если , то λ = 0. Единственность множителя λ очевидна: при умножении на разные числа мы получим различные векторы. Страницы: 1, 2 |
|
© 2010 |
|
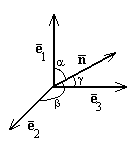
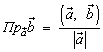 ; 3.
; 3. 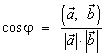 .
.