|
|
|
|
Реферат: Векторы
Реферат: Векторы
 дним из фундаментальных понятий современной математики являются
вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась
благодаря широкому использованию этого понятия в различных областях математики,
механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием
векторного исчисления и его приложений. Были созданы векторная алгебра и
векторный анализ, общая теория векторного пространства. Эти теории были
использованы при построении специальной и общей теории относительности, которые
играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора
стало одним из ведущих понятий школьного курса математики.
дним из фундаментальных понятий современной математики являются
вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась
благодаря широкому использованию этого понятия в различных областях математики,
механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием
векторного исчисления и его приложений. Были созданы векторная алгебра и
векторный анализ, общая теория векторного пространства. Эти теории были
использованы при построении специальной и общей теории относительности, которые
играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора
стало одним из ведущих понятий школьного курса математики.
  Что же такое вектор? Как ни странно, ответ на этот вопрос
представляет известные затруднения. Существуют различные подходы к определению
понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь
для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут
иметься различные взгляды на это понятие. Разумеется, какое бы определение мы
ни взяли, вектор – с элементарно-геометрической точки зрения - есть
геометрический объект, характеризуемый направлением ( т.е. заданной с точностью
до параллельности прямой и направлением на ней) и длиной. Однако такое
определение является слишком общим, не вызывающим конкретных геометрических
представлений. Согласно этому общему определению параллельный перенос можно
считать вектором. И действительно, можно было бы принять такое определение
: «Вектором называется всякий параллельный перенос». Это определение
логически безупречно, и на его основе может быть построена вся теория действий
над векторами и развиты приложения этой теории. Однако это определение,
несмотря на его полную конкретность , нас здесь также не может удовлетворить,
так как представление о векторе как о геометрическом преобразовании кажется нам
недостаточно наглядным и далеким от физических представлений о векторных
величинах.
Что же такое вектор? Как ни странно, ответ на этот вопрос
представляет известные затруднения. Существуют различные подходы к определению
понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь
для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут
иметься различные взгляды на это понятие. Разумеется, какое бы определение мы
ни взяли, вектор – с элементарно-геометрической точки зрения - есть
геометрический объект, характеризуемый направлением ( т.е. заданной с точностью
до параллельности прямой и направлением на ней) и длиной. Однако такое
определение является слишком общим, не вызывающим конкретных геометрических
представлений. Согласно этому общему определению параллельный перенос можно
считать вектором. И действительно, можно было бы принять такое определение
: «Вектором называется всякий параллельный перенос». Это определение
логически безупречно, и на его основе может быть построена вся теория действий
над векторами и развиты приложения этой теории. Однако это определение,
несмотря на его полную конкретность , нас здесь также не может удовлетворить,
так как представление о векторе как о геометрическом преобразовании кажется нам
недостаточно наглядным и далеким от физических представлений о векторных
величинах.
 Итак,
вектором Итак,
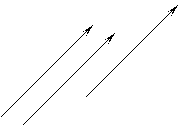
вектором называется семейство всех параллельных между собой одинаково направленных и
имеющих одинаковую длину отрезков (рис.1). Вектор изображают на
чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков,
представляющее собой вектор, а лишь один из этих отрезков). Для обозначения
векторов в книгах и статьях применяют жирные латинские буквы а,
в, с и так далее, а в тетрадях и на доске – латинские буквы с
черточкой сверху,
называется семейство всех параллельных между собой одинаково направленных и
имеющих одинаковую длину отрезков (рис.1). Вектор изображают на
чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков,
представляющее собой вектор, а лишь один из этих отрезков). Для обозначения
векторов в книгах и статьях применяют жирные латинские буквы а,
в, с и так далее, а в тетрадях и на доске – латинские буквы с
черточкой сверху, 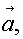 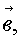 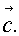
    Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой
без черточки) обозначают длину вектора. Длину иногда обозначают также
вертикальными черточками – как модуль (абсолютную величину) числа. Таким
образом, длина вектора а обозначается через а или
IаI, а в рукописном тексте длина
вектора а обозначается через а или I
аI. В связи с изображением векторов в виде
отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор,
неравноправны: одного конца отрезка к другому. Различают
начало и конец вектора (точнее, отрезка, изображающего вектор).
Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой
без черточки) обозначают длину вектора. Длину иногда обозначают также
вертикальными черточками – как модуль (абсолютную величину) числа. Таким
образом, длина вектора а обозначается через а или
IаI, а в рукописном тексте длина
вектора а обозначается через а или I
аI. В связи с изображением векторов в виде
отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор,
неравноправны: одного конца отрезка к другому. Различают
начало и конец вектора (точнее, отрезка, изображающего вектор).
   Весьма часто понятию вектора дается другое определение:
вектором называется направленный отрезок. При этом векторы (т.е.
направленные отрезки), имеющие одинаковую длину и одно и то же направление
(рис.3), уславливаются считать равными.
Векторы называются одинаково направленными, если их полупрямые одинаково
направлены.
Сложение векторов.
Все сказанное пока еще не дает понятие вектора достаточно содержательным и
полезным. Большую содержательность и богатую возможность приложений понятие
вектора получает тогда, когда мы вводим своеобразную «геометрическую
арифметику» – арифметику векторов, позволяющую складывать векторы, вычитать их
и производить над ними целый ряд других операций. Отметим в связи с этим, что
ведь и понятие числа становится интересным лишь при введении арифметических
действий, а не само по себе.
Суммой векторов а и в с координатами а1,
а2 и в1, в2 называется вектор с с координатами а1 + в1,
а2 + в2, т.е.
а (а1; а2) + в (в1;в2) = с (а1 + в1; а2 + в2).
Следствие:
а + в = в + а , (коммутативность)
а + ( в + с ) = (а + в) + с. (ассоциативность)
Весьма часто понятию вектора дается другое определение:
вектором называется направленный отрезок. При этом векторы (т.е.
направленные отрезки), имеющие одинаковую длину и одно и то же направление
(рис.3), уславливаются считать равными.
Векторы называются одинаково направленными, если их полупрямые одинаково
направлены.
Сложение векторов.
Все сказанное пока еще не дает понятие вектора достаточно содержательным и
полезным. Большую содержательность и богатую возможность приложений понятие
вектора получает тогда, когда мы вводим своеобразную «геометрическую
арифметику» – арифметику векторов, позволяющую складывать векторы, вычитать их
и производить над ними целый ряд других операций. Отметим в связи с этим, что
ведь и понятие числа становится интересным лишь при введении арифметических
действий, а не само по себе.
Суммой векторов а и в с координатами а1,
а2 и в1, в2 называется вектор с с координатами а1 + в1,
а2 + в2, т.е.
а (а1; а2) + в (в1;в2) = с (а1 + в1; а2 + в2).
Следствие:
а + в = в + а , (коммутативность)
а + ( в + с ) = (а + в) + с. (ассоциативность)
  Для доказательства коммутативности сложения векторов на плоскости
необходимо рассмотреть пример.
а и в – векторы (рис.5).
Пусть ОА =а, ОВ = в.
Для доказательства коммутативности сложения векторов на плоскости
необходимо рассмотреть пример.
а и в – векторы (рис.5).
Пусть ОА =а, ОВ = в.
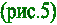 1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.
2. а = ОА = ВС,
в = ОВ = АС, т.к. параллелограмм.
3. ОА + АС = ОВ + ВС = ОС, значит а + в = в + а. ч.т.д.
Для доказательства ассоциативности мы отложим от произвольной точки О
вектор ОА = а, от точки А вектор АВ = в и от
точки в – вектор ВС = с. Тогда мы имеем:
АВ + ВС =АС.
(а + в ) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС,
а + (в + с ) = ОА + (АВ + ВС) = ОА + АС = ОС,
откуда и следует равенство а + ( в + с ) = (а
+ в) + с. Заметим, что приведенное доказательство совсем не
использует чертежа. Это характерно ( при некотором навыке ) для решения задач
при помощи векторов.
Остановимся теперь на случае, когда векторы а и в
направлены в противоположные стороны и имеют равные длины; такие векторы
называют противоположными. Наше правило сложения векторов приводит к тому, что
сумма двух противоположных векторов представляет собой «вектор», имеющий
нулевую длину и не имеющий никакого направления; этот «вектор» изображается
«отрезком нулевой длины», т.е. точкой. Но это тоже вектор, который называется
нулевым и обозначается символом 0.
Равенство векторов.
Два вектора называются равными, если они совмещаются параллельным
переносом. Это означает, что существует параллельный перенос, который переводит
начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что разные векторы
одинаково направлены и равны по абсолютной величине.
И обратно: если векторы одинаково направлены и равны
по абсолютной величине, то они равны.
Действительно, пусть векторы АВ и С
D – одинаково направленные векторы, равные по абсолютной
величине (рис.6). Параллельный перенос, переводящий точку С в точку А,
совмещает полупрямую СD с полупрямой АВ, так как они
одинаково направлены. А так как отрезки АВ и CD равны, то
при этом точка D совмещается с точкой В, то есть
параллельный перенос переводит вектор CD в
вектор АВ. Значит, векторы АВ и С
D равны, что и требовалось доказать. 1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.
2. а = ОА = ВС,
в = ОВ = АС, т.к. параллелограмм.
3. ОА + АС = ОВ + ВС = ОС, значит а + в = в + а. ч.т.д.
Для доказательства ассоциативности мы отложим от произвольной точки О
вектор ОА = а, от точки А вектор АВ = в и от
точки в – вектор ВС = с. Тогда мы имеем:
АВ + ВС =АС.
(а + в ) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС,
а + (в + с ) = ОА + (АВ + ВС) = ОА + АС = ОС,
откуда и следует равенство а + ( в + с ) = (а
+ в) + с. Заметим, что приведенное доказательство совсем не
использует чертежа. Это характерно ( при некотором навыке ) для решения задач
при помощи векторов.
Остановимся теперь на случае, когда векторы а и в
направлены в противоположные стороны и имеют равные длины; такие векторы
называют противоположными. Наше правило сложения векторов приводит к тому, что
сумма двух противоположных векторов представляет собой «вектор», имеющий
нулевую длину и не имеющий никакого направления; этот «вектор» изображается
«отрезком нулевой длины», т.е. точкой. Но это тоже вектор, который называется
нулевым и обозначается символом 0.
Равенство векторов.
Два вектора называются равными, если они совмещаются параллельным
переносом. Это означает, что существует параллельный перенос, который переводит
начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что разные векторы
одинаково направлены и равны по абсолютной величине.
И обратно: если векторы одинаково направлены и равны
по абсолютной величине, то они равны.
Действительно, пусть векторы АВ и С
D – одинаково направленные векторы, равные по абсолютной
величине (рис.6). Параллельный перенос, переводящий точку С в точку А,
совмещает полупрямую СD с полупрямой АВ, так как они
одинаково направлены. А так как отрезки АВ и CD равны, то
при этом точка D совмещается с точкой В, то есть
параллельный перенос переводит вектор CD в
вектор АВ. Значит, векторы АВ и С
D равны, что и требовалось доказать.
 Скалярное произведение двух векторов и его свойства.
Скалярным произведением двух нулевых векторов называется число, равное
произведению числовых значений длин этих векторов на косинус угла между
векторами.
Обозначение: а х в = IaI * IbI * cos ( а, в).
Свойства скалярного произведения:
1. а х в = в х а.
2. Для того, чтобы два нулевых вектора а и в
были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих
векторов было равно нулю, т.е. а х в = 0.
3. Выражение а х а будем обозначать а2 и называть скалярным квадратом вектора а.
Свойства операций над векторами.
Имеют место следующие теоремы об операциях над векторами, заданными в
координатной форме.
1. Пусть даны а = (ах, аy, аz
) и в = ( вx, ву, в
z), тогда сумма этих векторов есть вектор с,
координаты которого равны сумме одноименных координат слагаемых векторов, т.е.
с = а + в = (ах + вx; а
y + ву; аz + вz).
Пример 1.
а = ( 3; 4; 6) и в = ( -1; 4; -3), тогда с = ( 3 +
( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3).
2. а = (ах, аy, аz
) и в = ( вx, ву, в
z), тогда разность этих векторов есть вектор с
, координаты которого равны разности одноименных координат данных векторов, т.е.
с = а - в = (ах - вx; а
y - ву; аz - вz).
Пример 2.
а = ( -2; 8; -3) и в = ( -4; -5; 0), тогда с =
а – в = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = = ( 2; -13; -3).
3. При умножении вектора а = (ах, аy,
аz) на число м все его координаты
умножаются на это число, т.е. ма = ( мах, маy,
маz).
Пример 3.
а = ( -8; 4; 0) и м = 3, тогда 3а = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0).
Понятие вектора, которое нашло широкое распространение в прикладных науках,
явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил
упростить изложение некоторых сложных геометрических понятий, доказательства
некоторых теорем школьного курса геометрии, позволил создать особый метод
решения различных геометрических задач.
Рассмотрим доказательство некоторых теорем с помощью векторов.
Теорема 1.
Диагонали ромба взаимно перпендикулярны.
Доказательство.
Скалярное произведение двух векторов и его свойства.
Скалярным произведением двух нулевых векторов называется число, равное
произведению числовых значений длин этих векторов на косинус угла между
векторами.
Обозначение: а х в = IaI * IbI * cos ( а, в).
Свойства скалярного произведения:
1. а х в = в х а.
2. Для того, чтобы два нулевых вектора а и в
были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих
векторов было равно нулю, т.е. а х в = 0.
3. Выражение а х а будем обозначать а2 и называть скалярным квадратом вектора а.
Свойства операций над векторами.
Имеют место следующие теоремы об операциях над векторами, заданными в
координатной форме.
1. Пусть даны а = (ах, аy, аz
) и в = ( вx, ву, в
z), тогда сумма этих векторов есть вектор с,
координаты которого равны сумме одноименных координат слагаемых векторов, т.е.
с = а + в = (ах + вx; а
y + ву; аz + вz).
Пример 1.
а = ( 3; 4; 6) и в = ( -1; 4; -3), тогда с = ( 3 +
( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3).
2. а = (ах, аy, аz
) и в = ( вx, ву, в
z), тогда разность этих векторов есть вектор с
, координаты которого равны разности одноименных координат данных векторов, т.е.
с = а - в = (ах - вx; а
y - ву; аz - вz).
Пример 2.
а = ( -2; 8; -3) и в = ( -4; -5; 0), тогда с =
а – в = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = = ( 2; -13; -3).
3. При умножении вектора а = (ах, аy,
аz) на число м все его координаты
умножаются на это число, т.е. ма = ( мах, маy,
маz).
Пример 3.
а = ( -8; 4; 0) и м = 3, тогда 3а = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0).
Понятие вектора, которое нашло широкое распространение в прикладных науках,
явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил
упростить изложение некоторых сложных геометрических понятий, доказательства
некоторых теорем школьного курса геометрии, позволил создать особый метод
решения различных геометрических задач.
Рассмотрим доказательство некоторых теорем с помощью векторов.
Теорема 1.
Диагонали ромба взаимно перпендикулярны.
Доказательство.
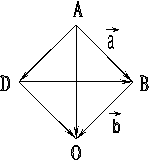
           Пусть АВСD – данный ромб (рис.7). Введем обозначения
: АВ = а, ВС = в. Из определения ромба:
АВ = DC = а, AD = ВС =
в.
Пусть АВСD – данный ромб (рис.7). Введем обозначения
: АВ = а, ВС = в. Из определения ромба:
АВ = DC = а, AD = ВС =
в.
     По определению суммы и разности векторов АС = а + в; DВ = а – в. По определению суммы и разности векторов АС = а + в; DВ = а – в.
        Рассмотрим АС * DВ = (а + в )( а – в) = а2 – в2 . Рассмотрим АС * DВ = (а + в )( а – в) = а2 – в2 .
     Так как стороны ромба равны, то а = в. Следовательно, AC * DB
=0. Из последнего получаем АС
Так как стороны ромба равны, то а = в. Следовательно, AC * DB
=0. Из последнего получаем АС  DВ, т.е. DB АС. Ч.т.д.
DВ, т.е. DB АС. Ч.т.д.
 Рассмотрим теперь решение задач с помощью векторов.
Задача 1.
Даны два вектора AB и CD,
причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2;
1;5). Рассмотрим теперь решение задач с помощью векторов.
Задача 1.
Даны два вектора AB и CD,
причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2;
1;5).
 Определить, перпендикулярны они друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD = (3; 3; 3).
Вычислим теперь скалярное произведение этих векторов:
АВ х СD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее и означает, что АВ СD.
Задача 2. Определить, перпендикулярны они друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD = (3; 3; 3).
Вычислим теперь скалярное произведение этих векторов:
АВ х СD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее и означает, что АВ СD.
Задача 2.
 Дан произвольный треугольник АВС. Доказать, что можно построить
треугольник, стороны которого равны и параллельны медианам треугольника АВС.
Решение.
Обозначим медианы треугольника АВС через ВЕ, СF и
обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с
:
ВС = а, СА = в, АВ = с
(рис.8). Тогда
АD = АВ + ВD = АВ +
Дан произвольный треугольник АВС. Доказать, что можно построить
треугольник, стороны которого равны и параллельны медианам треугольника АВС.
Решение.
Обозначим медианы треугольника АВС через ВЕ, СF и
обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с
:
ВС = а, СА = в, АВ = с
(рис.8). Тогда
АD = АВ + ВD = АВ +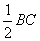 = с + = с + 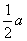 аналогично определяются и другие медианы:
ВЕ = а +
аналогично определяются и другие медианы:
ВЕ = а + 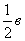 , СF = в + , СF = в + 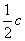 Так как, в силу условия замкнутости
ВС + СА + АВ = а + в + с =0,
то мы имеем:
АD + ВЕ + СF = ( с +
Так как, в силу условия замкнутости
ВС + СА + АВ = а + в + с =0,
то мы имеем:
АD + ВЕ + СF = ( с + 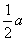 ) + (а + ) + (а + 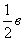 ) + ( в + ) + ( в + 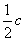 ) = ) = 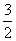 ( а + в + с) = ( а + в + с) = 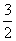 х 0 = 0.
Следовательно, отложив от точки В, вектор В1С1 = ВЕ и от точки С1 – вектор
С1D1 = СF, мы получим.
А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0.
А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является
замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого
равны и параллельны медианам АD, ВЕ, СF исходного треугольника.
Задача 3.
Доказать, что для любого треугольника имеет место формула
с2 = а2 + в2 – 2ав х соs С (теорема косинусов) х 0 = 0.
Следовательно, отложив от точки В, вектор В1С1 = ВЕ и от точки С1 – вектор
С1D1 = СF, мы получим.
А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0.
А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является
замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого
равны и параллельны медианам АD, ВЕ, СF исходного треугольника.
Задача 3.
Доказать, что для любого треугольника имеет место формула
с2 = а2 + в2 – 2ав х соs С (теорема косинусов)
 
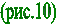 Решение.
Положим: а = СВ, в = СА,
с = АВ (рис.10).
Тогда с = а – в, и мы имеем
(учитывая, что угол между векторами а и в равен С):
с2 = ( а – в )2 = а2 – 2ав + в2 = а2 – 2ав х соs С + в2.
Задача 4.
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме
квадратов его сторон. Решение.
Положим: а = СВ, в = СА,
с = АВ (рис.10).
Тогда с = а – в, и мы имеем
(учитывая, что угол между векторами а и в равен С):
с2 = ( а – в )2 = а2 – 2ав + в2 = а2 – 2ав х соs С + в2.
Задача 4.
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме
квадратов его сторон.
 Решение.
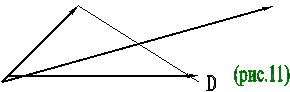
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства
АВ + AD = АС, АВ – АD = DВ.
Возведем эти равенства в квадрат. Получим:
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и
означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов
его сторон, что и требовалось доказать.
Задача 5.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1).
найдите такую точку D ( х; y
), чтобы векторы АВ и СD были равны.
Решение.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты
х – 0, y –1. Так как АВ = С
D, то х – 0 = -2, y –1 = -1.
Отсюда находим координаты точки D: х = -2,
y = 0.
Задача 6.
Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С
( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они
друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).
Вычислим теперь скалярное произведение этих векторов:
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее озночает, что АВ СD.
Рассмотренные выше примеры задач показывают, что векторный метод является
весьма мощных средством решения геометрических и многих физических (и
технических) задач.
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Используемая литература.
1. «Векторы в школьном курсе геометрии». (1976 г.)
В.А.Гусев. Ю.М.Колягин. Г.Л.Луканкин.
2. «Векторы в курсе геометрии средней школы. (1962 г.)
В.Г.Болтянский. И.М.Яглом.
Решение.
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства
АВ + AD = АС, АВ – АD = DВ.
Возведем эти равенства в квадрат. Получим:
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и
означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов
его сторон, что и требовалось доказать.
Задача 5.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1).
найдите такую точку D ( х; y
), чтобы векторы АВ и СD были равны.
Решение.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты
х – 0, y –1. Так как АВ = С
D, то х – 0 = -2, y –1 = -1.
Отсюда находим координаты точки D: х = -2,
y = 0.
Задача 6.
Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С
( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они
друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).
Вычислим теперь скалярное произведение этих векторов:
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее озночает, что АВ СD.
Рассмотренные выше примеры задач показывают, что векторный метод является
весьма мощных средством решения геометрических и многих физических (и
технических) задач.
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Используемая литература.
1. «Векторы в школьном курсе геометрии». (1976 г.)
В.А.Гусев. Ю.М.Колягин. Г.Л.Луканкин.
2. «Векторы в курсе геометрии средней школы. (1962 г.)
В.Г.Болтянский. И.М.Яглом.
|
|
|
|
|

 дним из фундаментальных понятий современной математики являются
вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась
благодаря широкому использованию этого понятия в различных областях математики,
механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием
векторного исчисления и его приложений. Были созданы векторная алгебра и
векторный анализ, общая теория векторного пространства. Эти теории были
использованы при построении специальной и общей теории относительности, которые
играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора
стало одним из ведущих понятий школьного курса математики.
дним из фундаментальных понятий современной математики являются
вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась
благодаря широкому использованию этого понятия в различных областях математики,
механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием
векторного исчисления и его приложений. Были созданы векторная алгебра и
векторный анализ, общая теория векторного пространства. Эти теории были
использованы при построении специальной и общей теории относительности, которые
играют исключительно важную роль в современной физике.
В соответствии с требованиями новой программы по математике понятие вектора
стало одним из ведущих понятий школьного курса математики.

 Что же такое вектор? Как ни странно, ответ на этот вопрос
представляет известные затруднения. Существуют различные подходы к определению
понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь
для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут
иметься различные взгляды на это понятие. Разумеется, какое бы определение мы
ни взяли, вектор – с элементарно-геометрической точки зрения - есть
геометрический объект, характеризуемый направлением ( т.е. заданной с точностью
до параллельности прямой и направлением на ней) и длиной. Однако такое
определение является слишком общим, не вызывающим конкретных геометрических
представлений. Согласно этому общему определению параллельный перенос можно
считать вектором. И действительно, можно было бы принять такое определение
: «Вектором называется всякий параллельный перенос». Это определение
логически безупречно, и на его основе может быть построена вся теория действий
над векторами и развиты приложения этой теории. Однако это определение,
несмотря на его полную конкретность , нас здесь также не может удовлетворить,
так как представление о векторе как о геометрическом преобразовании кажется нам
недостаточно наглядным и далеким от физических представлений о векторных
величинах.
Что же такое вектор? Как ни странно, ответ на этот вопрос
представляет известные затруднения. Существуют различные подходы к определению
понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь
для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут
иметься различные взгляды на это понятие. Разумеется, какое бы определение мы
ни взяли, вектор – с элементарно-геометрической точки зрения - есть
геометрический объект, характеризуемый направлением ( т.е. заданной с точностью
до параллельности прямой и направлением на ней) и длиной. Однако такое
определение является слишком общим, не вызывающим конкретных геометрических
представлений. Согласно этому общему определению параллельный перенос можно
считать вектором. И действительно, можно было бы принять такое определение
: «Вектором называется всякий параллельный перенос». Это определение
логически безупречно, и на его основе может быть построена вся теория действий
над векторами и развиты приложения этой теории. Однако это определение,
несмотря на его полную конкретность , нас здесь также не может удовлетворить,
так как представление о векторе как о геометрическом преобразовании кажется нам
недостаточно наглядным и далеким от физических представлений о векторных
величинах.

 Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой
без черточки) обозначают длину вектора. Длину иногда обозначают также
вертикальными черточками – как модуль (абсолютную величину) числа. Таким
образом, длина вектора а обозначается через а или
IаI, а в рукописном тексте длина
вектора а обозначается через а или I
аI. В связи с изображением векторов в виде
отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор,
неравноправны: одного конца отрезка к другому. Различают
начало и конец вектора (точнее, отрезка, изображающего вектор).
Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой
без черточки) обозначают длину вектора. Длину иногда обозначают также
вертикальными черточками – как модуль (абсолютную величину) числа. Таким
образом, длина вектора а обозначается через а или
IаI, а в рукописном тексте длина
вектора а обозначается через а или I
аI. В связи с изображением векторов в виде
отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор,
неравноправны: одного конца отрезка к другому. Различают
начало и конец вектора (точнее, отрезка, изображающего вектор).

 Весьма часто понятию вектора дается другое определение:
вектором называется направленный отрезок. При этом векторы (т.е.
направленные отрезки), имеющие одинаковую длину и одно и то же направление
(рис.3), уславливаются считать равными.
Векторы называются одинаково направленными, если их полупрямые одинаково
направлены.
Сложение векторов.
Все сказанное пока еще не дает понятие вектора достаточно содержательным и
полезным. Большую содержательность и богатую возможность приложений понятие
вектора получает тогда, когда мы вводим своеобразную «геометрическую
арифметику» – арифметику векторов, позволяющую складывать векторы, вычитать их
и производить над ними целый ряд других операций. Отметим в связи с этим, что
ведь и понятие числа становится интересным лишь при введении арифметических
действий, а не само по себе.
Суммой векторов а и в с координатами а1,
а2 и в1, в2 называется вектор с с координатами а1 + в1,
а2 + в2, т.е.
а (а1; а2) + в (в1;в2) = с (а1 + в1; а2 + в2).
Следствие:
а + в = в + а , (коммутативность)
а + ( в + с ) = (а + в) + с. (ассоциативность)
Весьма часто понятию вектора дается другое определение:
вектором называется направленный отрезок. При этом векторы (т.е.
направленные отрезки), имеющие одинаковую длину и одно и то же направление
(рис.3), уславливаются считать равными.
Векторы называются одинаково направленными, если их полупрямые одинаково
направлены.
Сложение векторов.
Все сказанное пока еще не дает понятие вектора достаточно содержательным и
полезным. Большую содержательность и богатую возможность приложений понятие
вектора получает тогда, когда мы вводим своеобразную «геометрическую
арифметику» – арифметику векторов, позволяющую складывать векторы, вычитать их
и производить над ними целый ряд других операций. Отметим в связи с этим, что
ведь и понятие числа становится интересным лишь при введении арифметических
действий, а не само по себе.
Суммой векторов а и в с координатами а1,
а2 и в1, в2 называется вектор с с координатами а1 + в1,
а2 + в2, т.е.
а (а1; а2) + в (в1;в2) = с (а1 + в1; а2 + в2).
Следствие:
а + в = в + а , (коммутативность)
а + ( в + с ) = (а + в) + с. (ассоциативность)

 Для доказательства коммутативности сложения векторов на плоскости
необходимо рассмотреть пример.
а и в – векторы (рис.5).
Пусть ОА =а, ОВ = в.
Для доказательства коммутативности сложения векторов на плоскости
необходимо рассмотреть пример.
а и в – векторы (рис.5).
Пусть ОА =а, ОВ = в.

 Рассмотрим теперь решение задач с помощью векторов.
Задача 1.
Даны два вектора AB и CD,
причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2;
1;5).
Рассмотрим теперь решение задач с помощью векторов.
Задача 1.
Даны два вектора AB и CD,
причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2;
1;5).
 Дан произвольный треугольник АВС. Доказать, что можно построить
треугольник, стороны которого равны и параллельны медианам треугольника АВС.
Дан произвольный треугольник АВС. Доказать, что можно построить
треугольник, стороны которого равны и параллельны медианам треугольника АВС.


 Решение.
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства
АВ + AD = АС, АВ – АD = DВ.
Возведем эти равенства в квадрат. Получим:
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и
означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов
его сторон, что и требовалось доказать.
Задача 5.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1).
найдите такую точку D ( х; y
), чтобы векторы АВ и СD были равны.
Решение.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты
х – 0, y –1. Так как АВ = С
D, то х – 0 = -2, y –1 = -1.
Отсюда находим координаты точки D: х = -2,
y = 0.
Задача 6.
Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С
( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они
друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).
Вычислим теперь скалярное произведение этих векторов:
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее озночает, что АВ СD.
Рассмотренные выше примеры задач показывают, что векторный метод является
весьма мощных средством решения геометрических и многих физических (и
технических) задач.
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Решение.
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства
АВ + AD = АС, АВ – АD = DВ.
Возведем эти равенства в квадрат. Получим:
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и
означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов
его сторон, что и требовалось доказать.
Задача 5.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1).
найдите такую точку D ( х; y
), чтобы векторы АВ и СD были равны.
Решение.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты
х – 0, y –1. Так как АВ = С
D, то х – 0 = -2, y –1 = -1.
Отсюда находим координаты точки D: х = -2,
y = 0.
Задача 6.
Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С
( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они
друг другу или нет.
Решение.
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).
Вычислим теперь скалярное произведение этих векторов:
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
Последнее озночает, что АВ СD.
Рассмотренные выше примеры задач показывают, что векторный метод является
весьма мощных средством решения геометрических и многих физических (и
технических) задач.
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.