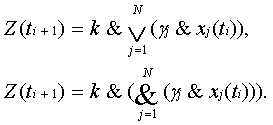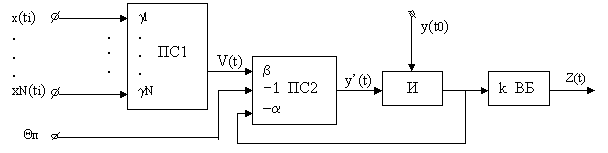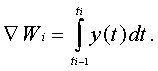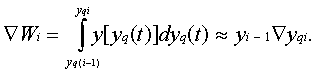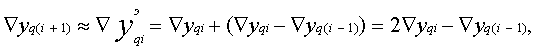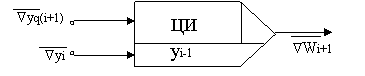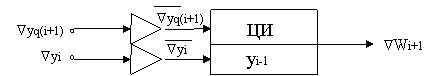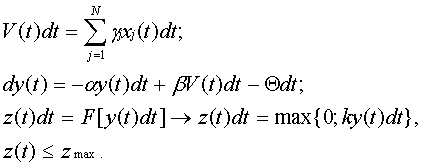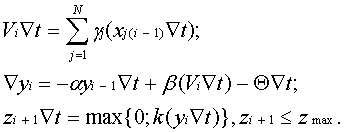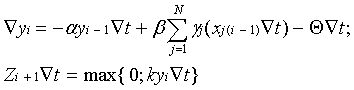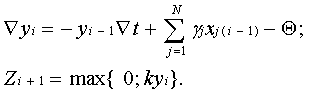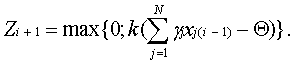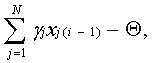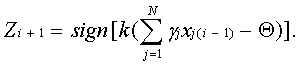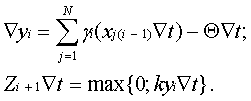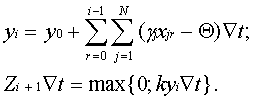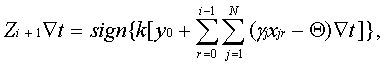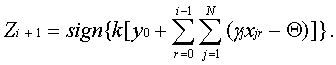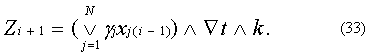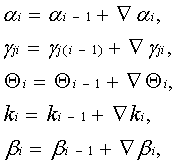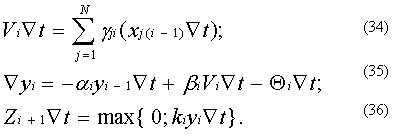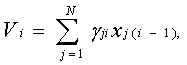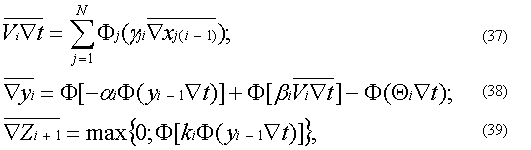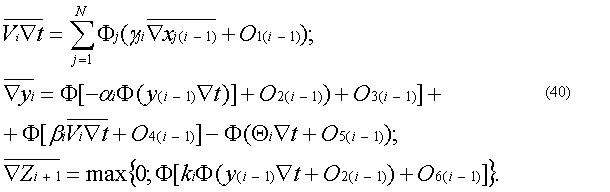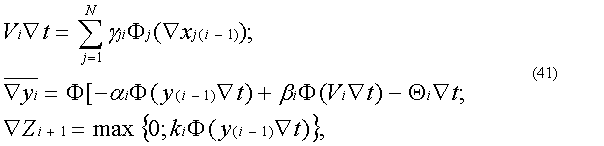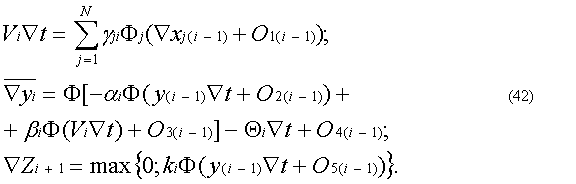Курсовая: Нейрокомпьютеры

Курсовая: Нейрокомпьютеры

Иными словами, изменяя величину порога Qп при gjÎ{0, 1} и k = 1, будем

менять вид логической функции Z(ti+1). Если же kÎ{0, 1}, то функции

(25), (26) принимают вид

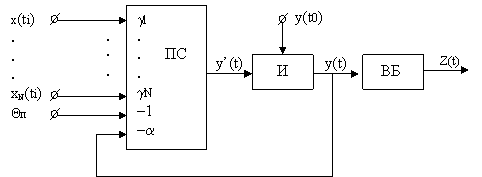
В тех случаях, когда синаптические веса gjÎ{0, 1, –1} или принимают

другие целочисленные значения, реализуемые формальным нейроном функции

усложняются.

Блок-схема формального нейрона приведена на рисунке 2. Она содержит два

блока: блок пространственной суммации (ПС) и блок формирования выходной

функции sign ky(ti), который, в свою очередь, может быть построен по

импульсному или статическому типу. В первом случае при выполнении условия

возбуждения нейрона (ky(ti)³0) на выходе появляется единичный сигнал

Z(ti+1) = e(t) априори заданной длительности t. После окончания этого сигнала

ФН переходит в невозбужденное состояние и остается в нем до следующего

выполнения условия возбуждения. Во втором случае при выполнении условия

ky(ti)³0 нейрон переходит в единичное состояние и остается в нем до

нарушения условия возбуждения.

В целом формально-логическая модель нейрона далека по своим возможностям от

ее естественного прототипа и не отражает всех его свойств, в частности не

учитывает процессов, протекающих на мембране нейрона. Данное обстоятельство

служит основанием для перехода к более совершенным нейроподобным элементам

динамического типа.

5.Динамические нейроны

Наиболее важным отличием нейроподобных элементов динамического типа –

динамических нейронов (ДН) от формальных нейронов является не столько учет в

них временной суммации (P’(t)¹0), сколько переход принципа «все или

ничего», характерного для отдельных спайков, к градуальному способу

кодирования информации. В соответствии с градуальным кодированием полагается,

что выходной величиной нейрона служит интенсивность выходных спайков,

которая, в свою очередь, зависит от количества и интенсивности входных

сигналов, а также от величины порога нервной клетки. То обстоятельство, что в

качестве входных и выходных величин при этом используются непрерывные

зависимости, позволяет представить информационные процессы в нервной клетке в

дифференциальной форме, т. е. в виде модели (10) или (12).

Блок-схема динамического нейрона, работающего в соответствии с алгоритмом

(12), приведена на рисунке 3. Наряду с пространственным сумматором ПС1,

формирующим сумму V(t) произведений gjxj(t), и пространственным сумматором

ПС2, вычисляющим производную y’(t), в схеме ДН предусмотрен интегрирующий

блок И для определения функции y(t), а также выходной блок ВБ, формирующий

выходную зависимость Z(t).

В тех случаях, когда b=1и k = 1, сумматоры ПС1 и ПС2 можно объединить и

представить схему на рисунке 3 в более простом виде, а именно так, как это

показано на рисунке 4. Если теперь реализовать схему 4 на сопротивлениях,

диодах и емкостях, то получим простейшую аналоговую модель динамического

нейрона.

Рис. 2. Формальный нейрон.

Рис. 3. Динамический нейрон, работающий в соответствии с алгоритмом 12

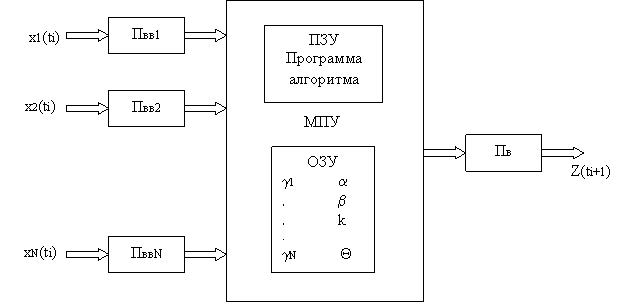
Рис.4. Динамический нейрон, упрощенный вариант.

Рассмотренные схемы могут строиться как на дискретных, так и на интегральных

элементах, а также в виде больших интегральных схем, содержащих десятки и

сотни ДН на кристалле. Эти схемы довольно просты и компактны, но

характеризуются неконтролируемым изменением параметров в функции от

температуры и других внешних факторов. Данное обстоятельство затрудняет их

использование в нейроподобных сетях больших размерностей. Более того, такие

элементы не позволяют создавать практически приемлемые схемы с переменными во

времени синаптическими весами и переменным порогом, т. к. Управляемое

изменение электрических сопротивлений связано с определенными техническими

трудностями. Все это стимулирует разработку и создание цифровых схем

динамических нейронов, свободных от указанных недостатков.

6.Цифровые модели нейронов

Одно из важных направлений в области построения цифровых нейроподобных

элементов связано с программированием универсальных ЭВМ, микроЭВМ,

персональных ЭВМ для реализации на них алгоритмов как отдельных нейронов, так

и их совокупностей, воспроизводящих информационные процессы в нейронных

ансамблях и нейронных сетях. Особых проблем при программировании систем

уравнений, основанных на алгоритмах типа (12), как правило, не возникает.

Однако имитация сугубо параллельных нейрофизиологических процессов на

последовательных ЭВМ связана с большими временными затратами, что не всегда

приемлемо с практической точки зрения. Поэтому применение ЭВМ классической

архитектуры для реализации сетей динамических нейронов весьма ограничено,

особенно в тех случаях, когда цифровая модель должна работать в реальном

масштабе времени, например при организации биоуправляемых экспериментов по

замене части нервной ткани ее имитационной моделью. Другая трудность

использования ЭВМ для моделирования нейронов и нейронных сетей состоит в том,

что любое изменение связей в моделируемой сети ведет к необходимости

составления новых программ.

Все это вынуждает искать способы построения таких цифровых устройств,

которые, с одной стороны, программно и аппаратно ориентированы на

воспроизведение алгоритма обработки информации в отдельной нервной клетке, а

с другой – пригодны для организации на их основе параллельных перестраиваемых

нейроподобных ансамблей и структур. Подобные устройства могут строиться на

базе современных однокристальных и секционированных микропроцессоров (МП).

Получающиеся при этом структуры цифровых нейронов (ЦН) приобретают

стандартный вид и могут быть представлены в виде схемы, показанной на рисунке

5.

Рис. 5. Структура цифрового нейрона.

Данная структура состоит из микропроцессорного устройства МПУ и подключенных

к нему N портов ввода Пввj (j = 1, N) и одного порта вывода Пв. Она

соответствует тому случаю, когда параметры gj ,b, k нейроподобной модели

являются постоянными. Предполагается также и то, что программа алгоритма (12)

хранится в постоянном запоминающем устройстве ПЗУ, а параметры, которые не

меняются в процессе работы конкретной модели цифрового нейрона, но могут быть

различными у разных ЦН, хранятся в оперативной памяти МПУ.

Входные величины xj(ti) в дискретные моменты времени ti = ti-1+dti (i = 1, 2,

...) записываются в соответствующие порты ввода Пввj рассматриваемого ЦН.

Поступают они с портов вывода других ЦН или из внешних сенсорных устройств в

цифровой форме и хранятся в Пввj в течение времени форме dti выполнения

алгоритма (12). После завершения работы алгоритма (12) в порт вывода

записывается значение функции Z(tj+1), которое в момент времени ti+1 по

жестким или перестраиваемым каналам связи передается в порты ввода других

цифровых нейронов.

Рассмотренная схема цифрового нейрона является довольно простой и ее

проектирование сводится по существу к программированию МП на языке

ассемблера. Однако техническая реализация нейроподобных сетей, состоящих из

таких ЦН, связана с определенными трудностями.

Во-первых, информация между различными ЦН передается в параллельных кодах,

что, в свою очередь, усложняет каналы передачи, особенно в тех случаях, когда

связи между нейронами необходимо оперативно менять при помощи устройств

электронной коммутации. Упрощение коммутирующих устройств за счет организации

передачи информации между ЦН в последовательных кодах ведет к существенной

потере производительности как отдельных нейроподобных элементов, так и

нейроподобной сети в целом.

Во-вторых, время работы отдельных ЦН существенно зависит от количества

синаптических весов. Если у различных ЦН число N различное, то и время их

работы будет различным. Следовательно, ЦН с минимальным числом входов будет

использоваться неэффективно.

И в-третьих, существенные трудности возникают в том случае, когда

синаптические веса модели нейронов являются переменными во времени. Для

формирования текущих значений gj(ti ) необходимо включить N дополнительных

портов ввода, в которые следует записывать не сами синаптические веса, а их

приращения.

Отмеченные обстоятельства являются серьезным обстоятельством не пути создания

удобных в эксплуатации цифровых нейроподобных элементов на базе

микропроцессоров и микроЭВМ универсального типа. По этой причине возникает

необходимость в разработке ЦН на основе специализированных устройств,

ориентированных на воспроизведение алгоритма (12).

Одним из перспективных подходов при этом может служить использование для

синтеза ЦН идей и методов построения цифровых моделей на базе интегрирующих

структур ЦИС. Это связано с тем, что в основе моделируемых динамических

нейрональных процессов лежат дифференциальные зависимости, а ЦИС, в свою

очередь, проблемно-ориентированны на решение систем линейных и нелинейных

дифференциальных уравнений.

Кроме того, цифровые интегрирующие структуры состоят из параллельно

функционирующих решающих блоков, информация между которыми передается в виде

последовательностей дискретных сигналов, имеющих смысл приращения выходных

зависимостей. Отдельные решающие блоки реализуют операции суммирования,

численного интегрирования, экстраполяции выходных приращений и, как правило,

снабжены коммутационными элементами. Благодаря этому на решающих блоках ЦИС

могут быть построены цифровые динамические нейроны, реализующие алгоритм (12)

с переменными синаптическими весами и соединяемые друг с другом при помощи

гибкой электронной коммутации. Следовательно, такие элементы будут свободны

от недостатков микропроцессорных ЦН.

7.Операции в цифровых интеграторах

Вышеперечисленные операции могут быть выполнены на элементной базе ЦИС. В

состав этой базы входят комбинационные сумматоры, цифровые интеграторы и

нелинейные блоки. Цифровой интегратор представляет собой устройство,

осуществляющее численное интегрирование подынтегральной функции y(t).

Аргумент t предварительно квантуется с постоянным шагом dt=ti–ti-1 (i=1,

2,...), начиная с t0. Поэтому для произвольного значения ti будем иметь

ti=t0+idt.

Функция y(ti)= yi, определяемая на множестве дискретных значений ti, является

решетчатой. Для данной функции вместо дифференциального применяется

разностный оператор, в частности построенный на основе первых разностей. Эти

разности могут быть нисходящими (интерполяция) и восходящими (экстраполяция).

В случае нисходящих разностей имеем

Dyi=yi+1–yi или yi=yi+1–Dyi,

а в случае восходящих разностей –

Ñyi=yi–yi-1 или yi=yi-1+Ñyi.

В теории цифровых интегрирующих структур используются восходящие разности и

считается, что цифровой интегратор на каждом временном интервале

Ñt=dt=ti–ti-1 вычисляет приращение Wi интеграла W Римана:

При использовании простейшей формулы численного интегрирования – формулы

Эйлера для интеграла Римана будем иметь

ÑWi»yi-1Ñt.

При интегрировании в соответствии с более сложным интегралом Стилтьеса, когда

интегрирование ведется по некоторой функции yq(t), получим

Таким образом, при использовании формулы Эйлера отдельный цифровой

интегратор реализует аппаратным методом следующие уравнения:

yi=yi-1+Ñyi;

ÑWi+1=yiÑyq(i+1).

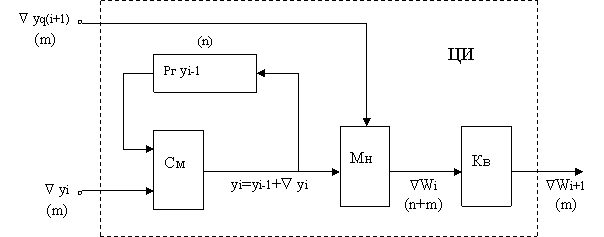
В связи с тем, что значение приращения Ñyq(i+1) в i-м шаге неизвестно,

его либо экстраполируют, например по линейному закону:

либо принимают равным Ñyqi.

В тех случаях, когда Ñyqi =Ñt, цифровой интегратор

воспроизводит численное интегрирование по Риману

yi=Ñyi-1+Ñyi;

ÑWi+1 =yiÑt.

Очевидно, что при постоянном шаге Ñt экстраполяция приращений

независимой переменной t не требуется.

8.Структура цифровых интеграторов

Структура ЦИ, инвариантная относительно интегрирования по Риману или по

Стилтьесу, может быть представлена в виде схемы, показанной на рисунке 6.

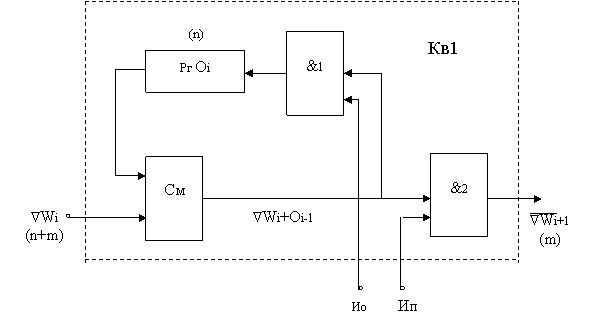
Рис.6. Структурная схема ЦИ

Цифровой интегратор состоит из двухвходового сумматора См, регистра Рг,

множителя Мн и квантователя Кв, формирующего квантованные приращения

ÑWi+1.

Суть квантования состоит в том, что при умножении n-разрядных величин yi на

m-разрядные величины Ñyq(i+1) получаются n+m разрядные приращения

ÑWi+1. Для того, чтобы эти приращения можно было использовать в

качестве m-разрядных значений Ñyi , Ñyq(i+1) на входах того же

или другого ЦИ, необходимо из n+m разрядов выделить m старших. Такое

выделение называется квантованием. Математически его можно записать так:

ÑWi+1=П[ÑWi]m – приращение интеграла;

Oi =O[ÑWi]n – остаток квантования.

С целью уменьшения погрешности, возникающей при квантовании (округлении)

величин ÑWi, остатки Oi, как правило, при квантовании не

отбрасываются, а учитываются в соответствии со следующим алгоритмом:

ÑWi+1=П[ÑWi + Oi-1]m ;

Oi =O[ÑWi + Oi-1]n.

Схема квантователя Кв1, реализующего данный алгоритм, приведена на рисунке 7.

Рис.7. Квантователь

Предполагается, что приращения ÑWi, ÑWi+1 представлены в

последовательных кодах, а длительности сигналов Ио, Ип и временные

соотношения между ними выбраны так, чтобы на выходе квантователя появлялись

m-разрядные квантованные приращения ÑWi+1, а в регистре Рг0

формировались n-разрядные остатки.

В дальнейшем процедуру квантования будем обозначать оператором Ф. Тогда в

случае квантования с сохранением остатков запишем:

ÑWi+1=Ф[ÑWi + Oi-1]= ÑWi + Oi-1– Oi;

а при квантовании с сохранением остатков будем иметь

ÑWi +1=Ф[ÑWi]= ÑWi – Oi.

Схема квантователя без сохранения остатков имеет более простой, чем на рис.

7, вид (рис.8):

Рис.8 Квантователь (без сохранения остатков)

В дальнейшем будем полагать, что в качестве квантователя используется схема

Кв1. Условное графическое обозначение ЦИ с таким квантователем приведено на

рис. 9.

Рис.9. Цифровой интегратор, условное обозначение

Интегратор без квантователя, отдельный квантователь (Кв), интегратор с

квантователями на входах и экстраполятор приращений (Э) будем обозначать так,

как это показано на рис. 10 (а, б, в, г) соответственно.

а) Интегратор без квантователя б)

Отдельный квантователь

в) Интегратор с квантователями на входах

г) Экстраполятор приращений

Рис. 10. Условные обозначения

9.Нейроэлементы на основе цифровых интеграторов

Для построения НЭ на базе цифровых интеграторов и сумматоров используем

математическую модель информационных процессов в нейроне, предварительно

представив ее в дифференциальной форме:

После квантования аргумента и перехода к восходящим разностям, получим

разностный алгоритм динамического НЭ:

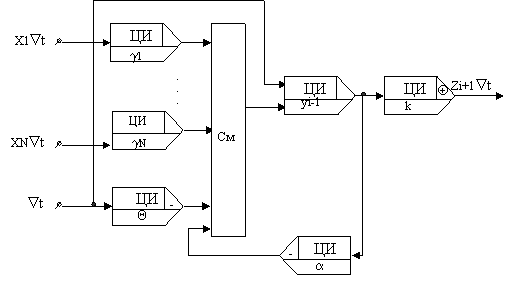
Цифровой нейроэлемент, воспроизводящий этот алгоритм на основе ЦИ, приведен

на рис. 11, где знак Å в последнем правом ЦИ обозначает операцию

выделения положительных значений kyiÑt(max{0; k(yiÑt)}).

Рис. 11. Цифровой нейроэлемент

Если положить b=0, то схема цифрового НЭ упрощается и принимает вид,

показанный на рис.12.

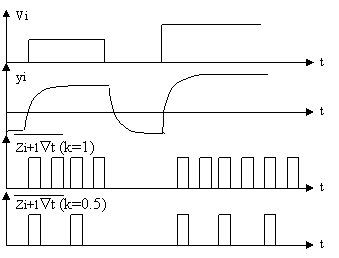
Рис. 12. Цифровой нейроэлемент, упрощенная схема

Временная диаграмма информационных процессов, протекающих в этой схеме, может

быть представлена так, как это показано на рис. 13, где полагается, что

приращения являются одноразрядными, т. е. m=1, Ñt=2–n. Из

рисунка видно, что цифровой НЭ действительно воспроизводит рассмотренную ранее

модель информационных процессов в нейроне.

Рис. 13. Временная диаграмма

10. Динамический цифровой нейроподобный элемент как нейроподобный процессор

Рассмотренные формальные и динамические искусственные нейроны воспроизводят

лишь отдельные фрагменты информационной деятельности нервных клеток.

Реализуются они структурным способом на элементной базе цифровой или

аналоговой техники. Такие нейроны узкоспециализированы и по этой причине не

могут служить процессорными элементами нейронных сетей.

Однако если их строить на основе разностного алгоритма динамического нейрона,

то появляется возможность создания универсальных нейроэлементов процессорного

типа– цифровых нейропроцессоров (ЦНП). Операционный базис ЦНП включает такие

специфические операции, как формальный нейрон, суммирующий нейрон,

динамический нейрон и т. п., а также такие крупные математические операции,

как скалярное произведение двух векторов, цифровое интегрирование и другие.

Действительно, рассмотрим разностный алгоритм цифрового динамического нейрона,

реализуемого на цифровых интеграторах с многоразрядными приращениями, т. е.

такими приращениями Ñq Î {Ñt, Ñy, ÑW},

которые принадлежат диапазону –1<Ñq<1. Для удобства анализа

представим этот алгоритм в виде двух уравнений:

(27)

и будем считать, что неравенство Zi+1£Zmax выполняется автоматически

из-за ограниченности разрядной сетки регистров цифровых схем.

Как следует из алгоритма (27), при b=1 цифровой нейроподобный элемент

воспроизводит рассмотренную ранее математическую модель информационных

процессов в нервной клетке с постоянным значениями параметров a, Q, g, k.

Однако техника цифровых интеграторов позволяет довольно просто изменять во

времени не

только синаптические веса g, но и коэффициент k, порог Q и даже такой параметр,

как a. В связи с этим представляет интерес анализ потенциальных возможностей

алгоритма (27) при различных значениях его параметров и прежде всего параметра

инерционности a (0£a£1), а также при различных величинах шага

Ñt.

Положим a=1, Ñt=1. Тогда система уравнений (27) принимает более

простой вид:

		(28)
	(29)
			(30)

Решение системы (28) может быть представлено в виде одного равенства:

В свою очередь, из соотношения (29) следует, что при Ñt=a=1 алгоритм

(27) становится алгоритмом элемента, выполняющего функции цифрового

сумматора, который осуществляет выделение положительных элементов

алгебраической суммы

умноженной на коэффициент k. Более того, если при принятых значениях a и

Ñt дополнительно положить Zi Î{0;1}, xji Î{0;1}, то

система уравнений (27) превратится в алгоритм формального нейрона

Рассмотрим теперь тот случай, когда в алгоритме (27) параметр a и Ñt

лежат в интервале от нуля до единицы (0<a<1, 0<Ñt<1).

Очевидно, что в этом случае решение системы уравнений (27) с методической

погрешностью m аппроксимирует решение исходной системы уравнений, в которой

gj(t)= gj и b=1. Цифровой нейроподобный элемент, реализующий алгоритм

(27),служит при этом цифровым аналогом инерционного звена первого порядка с

сумматором на входе и нелинейным блоком на выходе. Такой ЦНЭ называют цифровым

динамическим нейроном.

При 0<a<1 и Ñt=1 получим предельный случай цифрового аналога

инерционного звена первого порядка, т. е. тот случай, когда величина

методической погрешности m имеет максимальное значение.

Далее, полагая в алгоритме (27) a=0, 0<Ñt<1, 0£| gj

|£1, 0£| Q |£1, 0£| k |£1, найдем, что

рассматриваемый алгоритм превращается в алгоритм обычного цифрового

интегратора, имеющего блок выделения положительных приращений на выходе и

комбинационный сумматор на входе.

(31)

Действительно, цифровая модель в данном случае будет описываться следующей

системой разностных уравнений:

Решая систему (31) при начальных условиях y(0)=y0, xj(0)=xj0, найдем

Если в интеграторах используются одноразрядные приращения, то цифровая модель

реализует зависимость

(32)

Кроме того, полагая в последнем соотношении Ñt=1, будем иметь

Иными словами, алгоритм (27) в рассматриваемом случае совпадает с алгоритмом

пространственно-временного сумматора с функцией выделения положительных

величин на выходе.

Таким образом, на основании анализа разностного алгоритма (27) можно

заключить, что реализующая его цифровая модель, построенная на основе

решающих блоков ЦИС, обладает рядом положительных качеств, облегчающих ее

использование в условиях моделирования нейроподобных ансамблей и сетей.

Действительно, в отличие от импульсных и аналоговых устройств, такая модель

не содержит неконтролируемо изменяющихся параметров, имеет цифровую

регистровую память и позволяет без изменения конфигурации элемента влиять на

выполняемые им функции путем изменения параметра a и величины шага Ñt,

а также путем использования на выходе положительных многоразрядных или

одноразрядных приращений. Без изменения конфигурации связей между цифровым

интегратором и цифровым сумматором эта схема в принципе позволяет

моделировать цифровой динамический нейрон, формальный нейрон, нейрон с

пространственно-временной суммацией. Она позволяет реализовать режим

сумматора и цифрового интегратора с пространственным сумматором на входе.

Изменение режима работы элемента может осуществляться плавным или ступенчатым

изменением шага Ñt на интервале 0£Ñt£1 и изменением

величины a на 0£a£1. Более того, при Q=0, a=0, gj=0 и yi>0

цифровой нейроподобный элемент выполняет функции генератора величин

Zi+1Ñt=kyiÑt, т. е. выполняет функции нейрона, а при Ñt=0

превращается в элемент памяти. В последнем случае величина yi хранится в

регистре ЦНЭ без изменения. Для ее считывания необходимо положить k=1, gj=0,

Q=0, a=0 и подать Ñt=1, а для записи новой информации на одном из входов

r необходимо в течение одного шага интегрирования иметь синаптический вес

gr=1, а коэффициенты gj (j¹r) синаптических весов остальных входов –

равными нулю, a=0, Q=0, Ñt=1.

Следует отметить и еще одну особенность рассматриваемого алгоритма. Ее суть

состоит в том, что при 0£yi£1, Q=0, a=1, gjÎ{0, 1},

ÑtÎ{0, 1}, kÎ{0, 1}, xjiÎ{0, 1}, Zi+1Î{0,1}

цифровой нейроподобный элемент, реализующий алгоритм (27), в

(34)

(36)

(35)

функциональном отношении превращается в схему, выполняющую следующее

логическое выражение:

Последнее обстоятельство интересно в том отношении, что открывает

принципиальную возможность построения нейроподобных сетей, состоящих из

цифровых динамических нейронов, позволяющих при некоторых условиях выполнять

чисто алгебраические соотношения, свойственные логическим моделям.

Иными словами, разностный алгоритм (27) цифрового нейроподобного элемента

является довольно универсальным. Он может служить обобщением не только

динамических, но и формально-логических моделей. С учетом возможности

изменения параметров a, gj, Q, k, а в общем случае и параметра b:

этот алгоритм может быть представлен в следующем виде:

Причем приращения Ñai, Ñgji, ÑQi, Ñki, Ñbi

переменных параметров ai, gji, Qi, ki, bi, как и входные приращения xj(i-

1)Ñt могут формироваться либо на выходах других ЦНЭ в виде

последовательностей Zi+1Ñt, либо поступать извне по каналам сенсорных

систем.

Таким образом, цифровая модель нейрона, построенная на основе цифровых

интеграторов и сумматоров и воспроизводящая разностный алгоритм (34 – 36) с

переменными параметрами, обладает функциональной пластичностью и может

служить в качестве процессорного элемента, пригодного как для использования в

нейрокибернетических и нейрофизиологических исследованиях, так и для

использования в цифровых нейрокомпьютерных системах, ориентированных на

решение сложных задач вычислительной математики, робототехники и

искусственного интеллекта.

Важная особенность этих нейроэлементов состоит в том, что помимо работы в

режимах различных искусственных нейронов они способны структурно выполнять

ряд крупных математических операций, таких как определение скалярного

произведения двух векторов, численное интегрирование, выделение положительных

приращений интеграла.

Действительно, рассматривая алгоритм (34 – 36), нетрудно видеть, что соотношение

(34) представляет собой скалярное произведение двух векторов Гi= [g1i,

g2i,¼,gNi] и X=[x1i, x2i,¼,xNi]T , умноженное на шаг

Ñt. Следовательно, если в ЦНЭ наряду с основным выходом положительных

приращений Zi+1Ñt предусмотреть дополнительный выход приращений

ViÑt, то появится возможность одновременного использования ЦНЭ как

минимум в двух режимах: в режиме определения приращений ViÑt и в режиме

определения положительных приращений интеграла Zi+1Ñt. Организуя еще

один выход, а именно выход приращений yiÑt, получим дополнительный режим

– режим численного интегрирования без выделения положительных величин. При этом

следует подчеркнуть, что применение в схеме ЦНЭ дополнительных выходов не

только не исключает возможности его применения в рассмотренных ранее режимах

относительно основного выхода Zi+1Ñt, но и существенно расширяет его

функциональные возможности. Например, при a=Ñt=1 и при использовании в

ЦИ многоразрядных приращений, на основном выходе ЦНЭ формируется функция (29),

а в случае применения ЦИ с одноразрядными приращениями формируется функция

(30).

В то же время наличие первого дополнительного выхода обеспечивает возможность

одновременного использования того же ЦНЭ и в качестве блока, реализующего

вычисление скалярного произведения, т. к. на его первом дополнительном выходе

формируется сумма произведений:

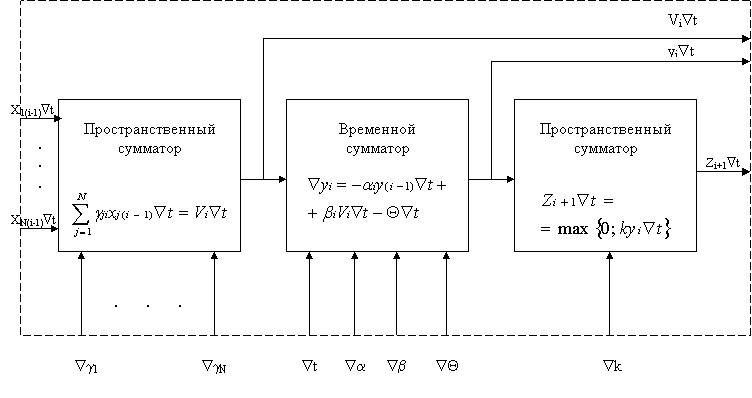
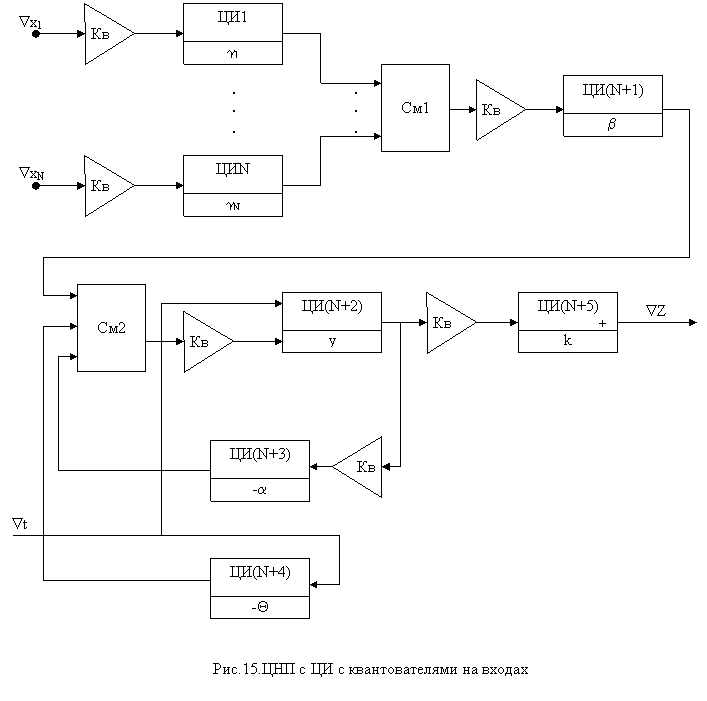
а на втором дополнительном выходе формируется величины:

Таким образом, в отличие от формальных и аналоговых динамических нейронов, в

которых постулируется отсутствие всяких взаимодействий между нервными

клетками, кроме синаптических, в предлагаемых цифровых нейроподобных

элементах допускаются подпороговые (соматические) взаимодействия, допускается

возможность модификации синаптических весов (g ji = gj(i-1) + Ñgji) за

счет дополнительных выходов yiÑt, а также возможность изменения других

параметров нейроподобной модели в функции как от основных, так и

дополнительных выходных величин.

Указанные обстоятельства позволяют рассматривать предлагаемый ЦНЭ с

дополнительными выходами и входами приращений параметров в качестве

специализированного нейроподобного процессора, операционный базис которого

составляют операции разностного алгоритма (34 – 36). Наиболее важным при этом

является то, что данный базис выбран не произвольно, а получен в результате

математического описания информационных процессов в нервной клетке и,

следовательно, является объективно обусловленным для мозга. Поэтому можно

предположить, что нейросети цифровых нейрокомпьютеров, составленные из

нейроподобных процессоров будут отличаться пластичностью, адаптивностью,

самоорганизацией, устойчивостью, т. е. теми свойствами, которые характерны

для систем мозга. А если так, то построенные на базе ЦНЭ нейрокомпьютеры

могут быть использованы не только в нейрофизиологических и

нейрокибернетических экспериментах, но и в исследованиях, направленных на

разработку принципов построения различных распознающих, вычислительных и

управляющих систем нейроподобного типа. Именно по этой причине идея

использования алгоритма (34–36) в качестве операционного базиса процессорных

элементов цифровых нейрокомпьютеров является весьма целесообразной. Цифровой

нейроподобный элемент, реализующий алгоритм (34–36) называют цифровым

нейроподобным процессором (ЦНП), или цифровым нейропроцессором.

11. Структура цифрового нейропроцессора

На основании разностного алгоритма (34–36) можно сделать вывод о том, что с

целью упрощения ЦНП его схему целесообразно строить на базе цифровых

интеграторов, реализующих формулу прямоугольников. Связано это с тем, что при

работе ЦНП в режиме ЦНЭ нет смысла применять более точные формулы

интегрирования, чем формула Эйлера, а возникающая при его работе в качестве

процессорного элемента нейрокомпьютеров погрешность может быть существенно

уменьшена, если отдельные ЦНП и нейрокомпьютер в целом использовать в

квазистационарном режиме. В целом структура ЦНП должна соответствовать

блок-схеме, приведенной на рисунке 14, где наряду с информационными входами и

входами приращений параметров предусмотрены как минимум три выхода, а именно

выходы приращений ViÑt, yiÑt, Zi

+1Ñt. Все эти выходы должны содержать квантователи и допускать

возможность их подсоединения как к информационным, так и управляющим входам

изменения параметров аналогичных процессоров. В связи с тем, что каждый

квантователь содержит определенное оборудование и вносит некоторую погрешность

в процесс функционирования ЦНП, вопрос о количестве квантователей и о месте их

включения в схеме6 процессора является весьма важным.

Рис.14. Структурная схема ЦНП

Учет процесса квантования приводит к более сложной, чем (34–36), системе

разностно-квантованных уравнений, которая в случае наиболее простого

квантования без сохранения остатков и при включении квантователей на выходах

ЦИ имеет следующий вид:

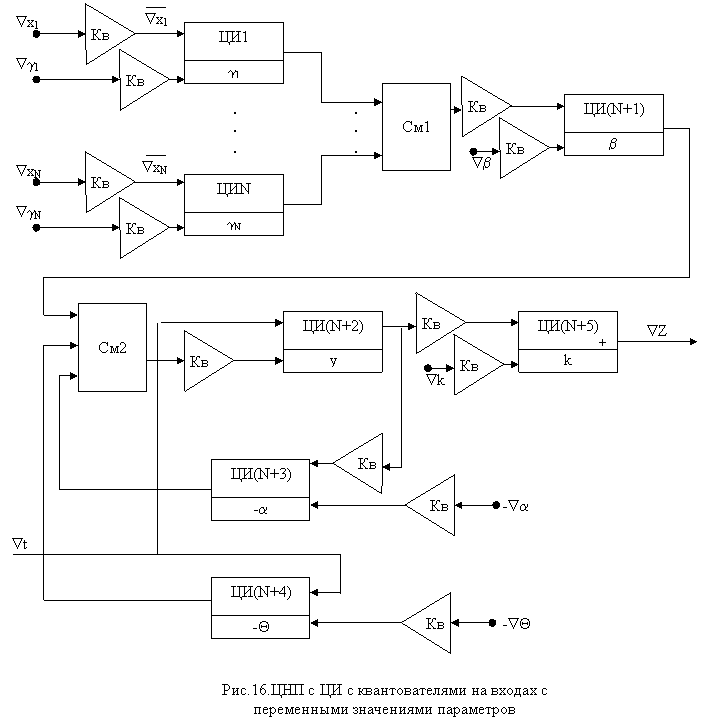
где Ф[Ñxi]=(Ñxi - Oi) – функция

квантования без сохранения остатков; Oi – остаток квантования.

Для определения закона изменения погрешности квантования необходимо из уравнения

(38) вычесть соответствующее ему разностное уравнение (35) и найти решение

получающегося при этом уравнения погрешности. Решение такого уравнения ci

=yi–yi представляет собой функцию квантования ЦНП. При

построении уравнения погрешности следует учитывать то, что система (37–39),

построенная на основе разностных уравнений (34–36), не является единстве, не

является единственно возможной.

Так, при использовании более точного способа квантования с сохранением остатков

F[Ñxi + Oi-1] = Ñxi + Oi-1 + Oi

получим систему разносто-квантованных уравнений, отличную от (37–39):

Далее, учитывая то, что наряду с включением квантователей на выходах ЦИ возможно

их включение на входах Ñyq, Ñyr

интеграторов, получим новые системы разностно-квантованных уравнений. В

частности, при квантовании без сохранения остатков и включении квантователей на

входах ЦИ будем иметь

а при квантовании с сохранением остатков и включении квантователей на входах

ЦИ получим:

Приведенные системы разностно-квантованных уравнений соответствуют различным

структурным схемам ЦНП. Если учесть, что каждую функцию квантования реализует

отдельный квантователь, причем квантователь без сохранения остатков проще

квантователя с сохранением остатков, то уже на основании соотношений (37–39),

(40), (41), (42) можно сравнить по сложности воспроизводящие их ЦНП.

Из рассмотрения этих соотношений можно заключить, что структуры ЦНП с

квантователями без сохранения остатков наиболее просты, а из структур с

сохранением остатков наиболее проста та, в которой квантование осуществляется

после суммирования. Следовательно, с точки зрения экономии оборудования

наиболее предпочтительны ЦНП, содержащие квантователи без регистров остатков.

Однако различные структуры процессоров неравноценны в отношении точности

вычислений.

Анализ рассматриваемых разносто-квантованных уравнений, проведенный при ai

=a, bi =b, Qi=Q, gji=gj, ki

=k показывает, что погрешность квантования ЦНП, квантователи которого

осуществляют квантование без сохранения остатков и включены на входах ЦИ, имеет

вид

где |ci | – модуль погрешности квантования; c0 – значение

погрешности ci при i=0; n – число разрядов переменной yi.

В случае квантования без сохранения остатков и при включении квантователей на

выходах ЦИ погрешность ЦНП можно оценить соотношением

Если квантователи включены на входах ЦИ, а квантование осуществляется с

сохранением остатков, то погрешность ЦНП может быть оценена следующим

образом:

При квантовании с сохранением остатков и квантователях на выходах ЦИ получим

В результате сравнения выражений (43), (44), (45), (46) можно заключить, что

погрешность квантования ЦНП, содержащих наиболее экономичные квантователи без

сохранения остатков, намного больше погрешности ЦНП, использующих квантование с

сохранением остатков. Действительно, как следует из соотношений (43), (44), в

них содержится произведение (aÑt)-1, которое при

0<Ñt<1, 0<a<1 может иметь довольно большие значения. Поэтому

в ЦНП в общем случае необходимо использовать ЦИ, реализующие квантование с

сохранением остатков.

Далее, из сравнения выражений (45), (46) видно, что погрешность процессора,

содержащего интеграторы с квантователями на входах, несколько меньше

погрешности ЦНП, построенного на основе ЦИ с квантователями на выходах.

Структура такого нейропроцессора приведена на рисунке 15.

Как видно из рисунка, N-входовый ЦНП содержит всего лишь N+4 квантователя.

Однако эта структура построена в предположении постоянства параметров a, b,

gj, Q, k, которые, в общем случае, могут быть переменными. Поэтому структура

с квантователями на входах должна быть более сложной и иметь вид, показанный

на рис. 16. Из рисунка 16 следует, что рассматриваемая структура содержит не

4+N, а 2(4+N) квантователей. Кроме того, такая структура менее удобна по

сравнению со структурой ЦНП с квантователями на выходах, поскольку

предполагает передачу между процессорами неквантованных приращений.

Альтернативный вариант построения нейропроцессора, а именно вариант ЦНП с

квантователями на выходах цифровых интеграторов может быть представлен в виде

схемы, приведенной на рис. 17. Здесь содержится N+5 квантователей и число это

Страницы: 1, 2, 3