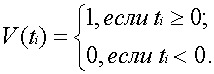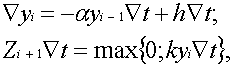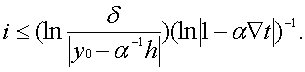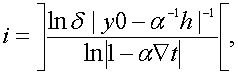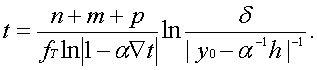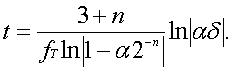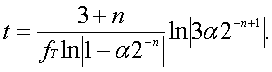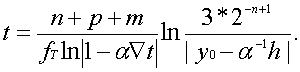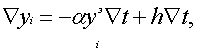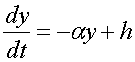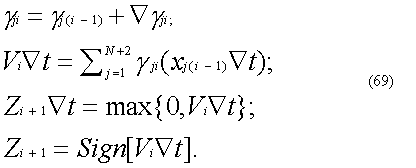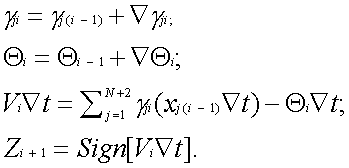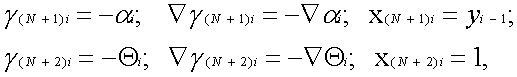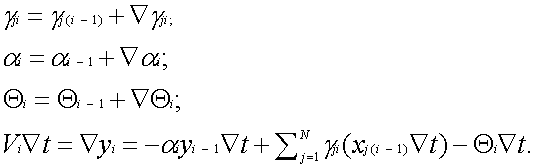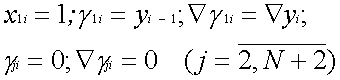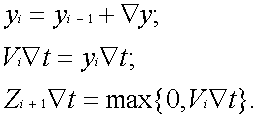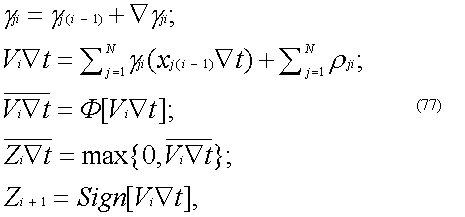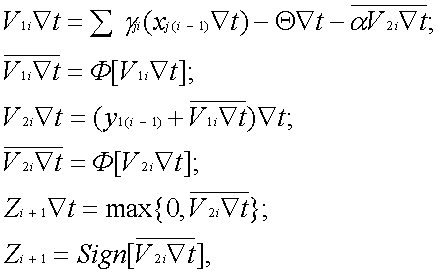|
РУБРИКИ |
Курсовая: Нейрокомпьютеры |
РЕКОМЕНДУЕМ |
||
|
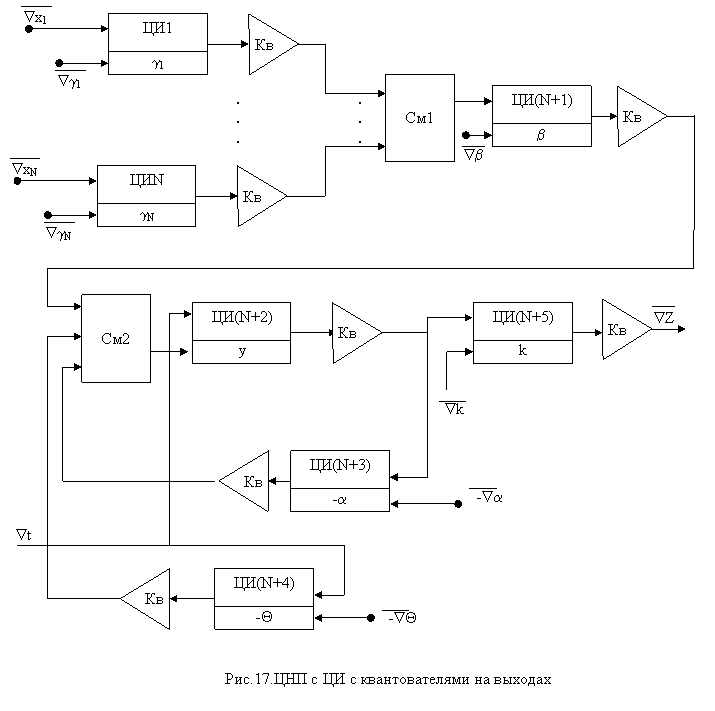
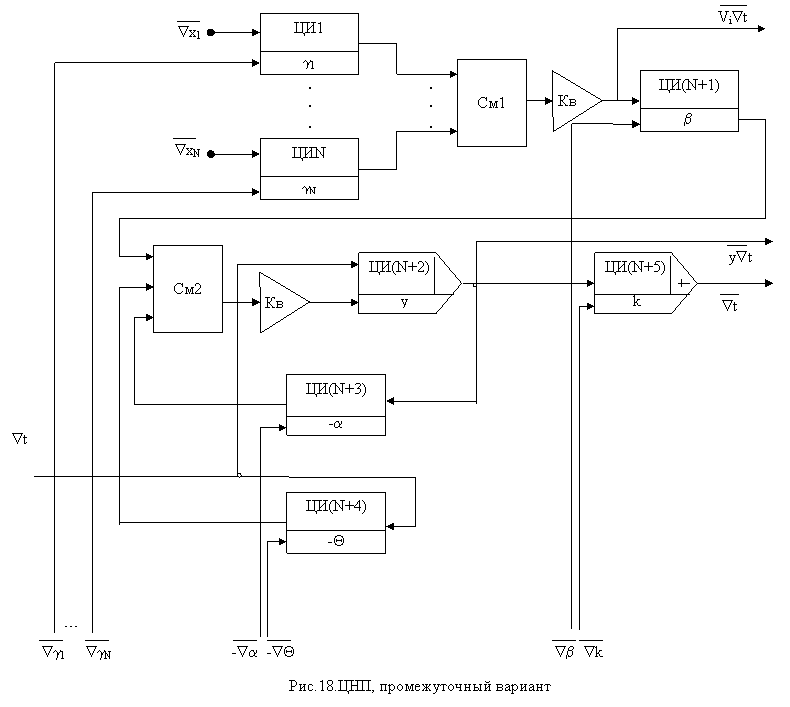
Курсовая: Нейрокомпьютерыинвариантно как при постоянных, так и при переменных значениях параметров. Приращения между ЦНП передаются в квантованном виде. Поэтому с точки зрения экономии оборудования и удобства эксплуатации вторая структура представляется более предпочтительной, поскольку передавать квантованные приращения проще и удобнее, чем неквантованные. Но то обстоятельство, что погрешность квантования в данной схеме больше, чем в схеме на рис.15, не позволяет считать ее оптимальной. По этой причине представляет интерес промежуточный вариант структуры ЦНП, у которого одна часть квантователей включена на выходах ЦИ, а другая часть на их входах. Структурная схема такого ЦНП приведена на рис.18. В этой схеме выходные приращения являются квантованными и, следовательно, проблем при их передаче между нейропроцессорами не возникает. Выходные приращения могут передаваться как на информационные входы, так и на входы изменения параметров. Далее, на входы сумматоров См1, См2 подаются неквантованные приращения. Данное обстоятельство не только позволяет исключить из схемы 3+N квантователей, но и уменьшить погрешность квантования, поскольку в соответствии с выражениями (43), (45) погрешность при суммировании неквантованных приращений меньше, чем при их суммировании после квантования. Таким образом, можно предположить, что данная структура ЦНП будет не только более экономичной (при N входах она содержит всего 4 квантователя), но и более точной. Отмеченные обстоятельства позволяют утверждать, что приведенная на рис.18 структура ЦНП является наиболее оптимальной. В связи с этим она используется в дальнейшем при синтезе конкретных схем цифровых нейропроцессоров. 12. Быстродействие цифрового нейропроцессора
Для оценки быстродействия ЦНП проанализируем его реакцию на ступенчатое входное воздействие, описываемое функцией
Пусть на входы ЦНП поступают такие постоянные во времени воздействия, алгебраическая сумма которых равна V(ti). С целью сокращения математических выкладок положим Qп = 0. Тогда, с учетом введенного допущения алгоритм (34 – 36) имеет вид где h = bV(ti); 0< b £1.
Из алгоритма (48, 49) видно, что быстродействие нейроподобного процессора определяется длительностью нестационарной составляющей решения уравнения (48). В свою очередь, это быстродействие тем выше, чем быстрее ЦНП переходит в новое устойчивое состояние, определяемое значениями h и a. Для оценки быстродействия ЦНП и выяснения зависимости времени переходного процесса в функции от таких параметров процессора, как тактовая частота его работы, разрядность регистров, точность отработки стационарного состояния, рассмотрим решение разностного уравнения (48). Это решение имеет вид Из равенства (50) следует, что стационарное решение a-1h, соответствующее входному суммарному входному воздействию h, будет получено тем быстрее, чем быстрее обратится в нуль произведение
Иными словами, при достижении требуемой точности вычислений будем иметь: где d = |yi – a-1h| – заданная погрешность вычислений.
Следовательно, быстродействие ЦНП можно оценить тем количеством шагов i, которое необходимо для удовлетворения неравенства (51). Определяя это количество шагов, получим
В дальнейшем соотношение (52) будем использовать в виде равенства где значение в скобках округляется до ближайшего большего целого числа. При определении времени отработки i шагов интегрирования в ЦНП, построенном на основе ЦИ, учтем то обстоятельство, что для реальных цифровых интеграторов справедливо соотношение
где T – время одного элементарного шага интегрирования. В свою очередь, время T определяется конструкцией ЦИ и для случая интеграторов последовательного типа может быть представлено в следующем виде:
где n – количество разрядов, отводимое под представление переменных; p – количество разрядов, необходимое для представления знака; m – количество разрядов, отводимое для представления приращений; fT – тактовая частота работы ЦИ.
Подставляя соотношения (54), (55) в (53), получим
Рассматривая последнее выражение, можно заключить, что для некоторой, априори заданной, погрешности вычислений d быстродействие ЦНП прямо пропорционально тактовой частоте работы ЦИ и обратно пропорционально количеству разрядов, используемых в их регистрах. Иными словами, чем меньше разрядов в процессоре, тем выше его быстродействие. Однако повышение быстродействия ЦНП путем сокращения разрядной сетки ЦИ связано с уменьшением точности его работы и имеет заранее известный предел. Имеет предел и возможность повышения тактовой частоты. Как правило, величина fT ограничена физическими возможностями применяемых микросхем. Другой способ повышения быстродействия ЦНП связан с подбором таких значений a и Ñt, при которых произведение aÑt » 1. Реализация этого способа требует специальных исследований. Поэтому для оценки быстродействия процессоров с фиксированной запятой рассмотрим зависимость времени отработки единичного входного воздействия в функции от количества разрядов n при различных значениях параметра a. При этом будем считать, что Ñt = 2-n; h = 1; y0 = 0.Тогда для ЦНП, построенного на интеграторах, работающих с модифицированными кодами (p = 2) и одноразрядными приращениями (m = 1), выражение (56) примет вид
Помимо числа разрядов n и параметра a в соотношение (57) входит тактовая частота fT и погрешность d, которая, в свою очередь, также зависит от числа разрядов n. В качестве fT выберем некоторую максимально возможную частоту fTM, а для выяснения
характера зависимости d = f(n) и определения формулы погрешности установившегося значения переходной характеристики ЦНП воспользуемся тем обстоятельством, что методическая погрешность стационарного состояния равна нулю и, следовательно, в качестве погрешности d в выражении (57) следует использовать только погрешность квантования. Более того, в качестве погрешности можно применять соотношение d=3*2-n+1 и считать, что формула, определяющая зависимость длительности переходного процесса в ЦНП с выходными одноразрядными приращениями в функции от числа
используемых в регистрах решающих блоков разрядов n, имеет следующий вид Формула (58) справедлива не только при отсутствии порога, но и при Qп ¹ 0. Особым является лишь момент превышения P(t) над порогом, поскольку только в этот момент появляются выходные сигналы, определяемые уравнением (36). Иными словами, формула (58) может быть использована для оценки времени изменения потенциала покоя, наступающего в результате подпорогового возбуждения ЦНП. Более того, эта зависимость удобна при подборе таких параметров нейроноподобного процессора, при которых он способен работать в реальном масштабе времени.
В более общем случае, для нейроноподобного процессора, использующего интеграторы с многоразрядными приращениями, выражение (58) несколько усложняется и принимает вид Выражение (59) представляет собой зависимость времени реакции ЦНП на входное ступенчатое воздействие в функции от его параметров. Эта зависимость является общим выражением, которое может быть использовано для оценки быстродействия цифровых нейроноподобных процессоров, реализованных на цифровых интеграторах. 13. Устойчивость функционирования цифрового нейропроцессора
Из соотношения (50) видно, что стационарное решение разностного уравнения (48) может быть получено лишь в том случае, если выполняется условие
Одновременно это же условие характеризует и устойчивость уравнения (35). Определяя диапазон возможных значений параметров a и Ñt, при которых выполняется неравенство (60), получим Иными словами, при выполнении условий (61) ЦНП устойчив.
Однако в полной мере этот вывод справедлив в предположении, что интеграторы, осуществляющие умножение на постоянные и переменные коэффициенты, безынерционны. На самом деле это не так. Как правило, ЦИ осуществляет задержку выходных приращений на один шаг дискретного времени ti. Последнее обстоятельство приводит к повышению порядка описывающего ЦНП уравнения и, как следствие, уменьшает его динамические возможности. Действительно, даже без учета задержек входной части ЦНП и при постоянном входном воздействии hÑt учет задержек ЦИ, осуществляющего умножение на параметр a, приводит к повышению порядка разностного уравнения (48) на единицу:
Из решения уравнения (62) находим, что оно устойчиво, если выполняются более жесткие условия, чем (61), а именно Таким образом, сравнивая ограничения (61) и (63), можно заключить, что реальная схема ЦНП устойчива при значениях шага Ñt, меньших, чем у ее идеального прототипа, описываемого уравнениями (34) – (36) или (48). Учет задержек, вносимых другими блоками умножения на постоянный коэффициент при замыкании основного выхода процессора на один из его информационных входов, приводит к еще большему повышению порядка, описывающего процессы в ЦНП разностного уравнения. В свою очередь, это приводит к еще большему уменьшению допустимой области устойчивой работы процессора. С увеличением задержки величина максимально допустимого шага уменьшается и, следовательно, уменьшается возможное быстродействие модели. Очевидно, что это обстоятельство необходимо учитывать при выборе шага Ñt. Однако в некоторых случаях более целесообразно не учитывать задержки блоков умножения на постоянные коэффициенты путем ограничения области устойчивой работы модели, а компенсировать их путем включения экстраполяторов приращений. Физическим аналогом экстраполяции может служить механизм воспроизведения акцептором результата действия, который по утверждению известного нейрофизиолога П. К. Анохина, является универсальным физиологическим механизмом, проявляющемся не только на уровне целого организма и его органов, но и на клеточном и даже внутриклеточном уровне. Ввиду того, что рассматриваемый ЦНП строится как информационная модель реального нейрона, можно предположить, что отмеченная необходимость в экстраполяции не является случайной, а есть отражение объективной закономерности, проявляющейся в компенсации инерционностей, возникающих в результате эволюционного усложнения биологических объектов на всех уровнях биологической организации от внутриклеточного до организменного включительно. В биологии такой компенсаторный механизм получил название опережающего отражения, в психологии он называется установкой, в математике и технике он известен как экстраполяция. Поэтому использование блоков экстраполяции для компенсации инерционностей отдельных блоков ЦНП может служить моделью опережающего отражения на внутриклеточном уровне.
Следуя идее П. К. Анохина, можно предположить, что компенсация инерционностей не только составных частей ЦНП, но и процессора в целом приведет к существенному расширению его динамических возможностей. Действительно, пусть процессор содержит экстраполятор, компенсирующий его собственную инерционность. Тогда процессы в ЦНП можно описать следующим разностным уравнением: где yiэ – экстраполированное на шаг вперед значение функции y(ti-1).
Учитывая то, что при точной экстраполяции yiэ = yi, получим
Решая уравнение (64) и определяя условие его устойчивости найдем:
Неравенство (65) выполняется, если справедливы условия: Иными словами, при использовании идеальных экстраполяторов, компенсирующих общую инерционность ЦНП, сам процессор приобретает способность устойчиво работать при любом положительном шаге без каких-либо ограничений на его величину.
Другой особенность экстраполяционного разностного уравнения (64) является то, что оно может быть устойчивым даже тогда, когда исходное разностное уравнение (48) и соответствующее ему дифференциальное уравнение вообще неустойчивы. Действительно, достаточным условием устойчивости уравнения (67) и необходимым условием устойчивости разностного уравнения (48) является выполнение условия: a<0. В противном случае решение уравнения (67) не имеет устойчивого стационарного значения y=a-1h, которое имеет место при a>0.
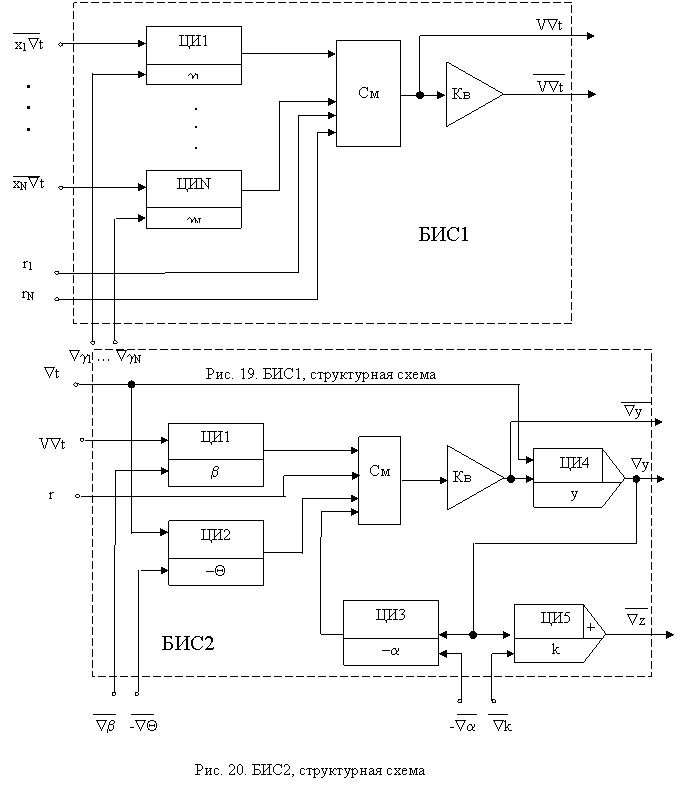
В то же время, из соотношения (65) следует, что уравнение (64) может быть устойчивым и при отрицательных a, если выполняется неравенство т. е. даже в тех случаях, когда уравнения (48) и (67) принципиально неустойчивы. Таким образом, ЦНП без инерционностей обладает широкими динамическими возможностями, что делает привлекательной идею построения процессоров, реализующих уравнение (64). Однако практическое воспроизведение точной экстраполяции связано с определенными техническими трудностями. Поэтому будем полагать, что задержки блоков умножения на постоянный или медленно меняющийся коэффициент при необходимости компенсируются экстраполяторами, а выходные приращения полного интегратора, реализующего временной сумматор ЦНП, в общем случае не экстраполируется. Подобная экстраполяция целесообразна лишь в том случае, когда приводит к улучшению динамических свойств, состоящих из ЦНП нейроноподобных ансамблей и структур. Используя полученные результаты, перейдем к рассмотрению вопросов создания элементной базы цифровых нейропроцессоров на основе микроэлектронной технологии. 14. Алгоритм и структура базового модуля цифрового нейропроцессора С целью практического использования рассматриваемых ЦНП целесообразно их изготовление на основе современной микроэлектронной технологии в виде больших интегральных схем (БИС). По этой причине уместна постановка задачи о разработке БИС, предназначенных не только для построения ЦНП, но и состоящих из них нейроподобных ансамблей и структур. Следуя морфологии отдельного нейрона, для отдельного ЦНП желательно иметь один корпус БИС. В то же время, учитывая то, что количество входных дендритных отростков у нервных клеток колеблется от единиц до десятков и сотен тысяч, в общем случае для БИС ЦНП необходимо предусматривать специальную БИС расширителя пространственного сумматора. При таком подходе номенклатура комплекта БИС ЦНП будет состоять из двух интегральных схем, а именно схемы собственно ЦНП, имеющей несколько информационных входов, и схемы входного расширителя, представляющего собой пространственный сумматор нейропроцессора. Вопрос о количестве входов каждого из корпусов БИС должен решаться исходя из возможностей конкретной микроэлектронной технологии. Пример одного из возможных вариантов построения таких схем приведен на рис.19 и на рис.20. Так, на рис.19 изображена структурная схема первого корпуса, а на рис.20 – второго корпуса БИС ЦНП (БИС1 и БИС2 соответственно). Однако необходимость в микросхемах двух типов ведет к определенным неудобствам при создании микроэлектронных ЦНП. Поэтому представляет интерес разработка алгоритма и структуры такого нейроподобного элемента, который будучи реализован в виде БИС мог служить базовым модулем при построении как временного, так и пространственного сумматоров, а значит, и нейропроцессора в целом. Для построения такого нейропроцессора используем подход, суть которого состоит в том, что для выполнения функций временного сумматора (БИС2) привлекается часть интеграторов, формирующих синаптические веса gji в БИС1. Данный подход позволяет на основе БИС1 синтезировать новую, отличную от БИС1 и БИС2 микросхему нейронного модуля, работающего в режиме простейшего нейрона и способного быть базовым элементом для синтеза более сложных нейропроцессоров динамического типа, а также выполнять функции расширителя входов пространственного сумматора ЦНП.
Действительно, как показывает анализ алгоритма (34–36), формирование дискретной функции yi из ее приращений Ñyi не отличается от формирования переменных синаптических весов gji , параметров ai , bi, переменного порога Qi и коэффициента ki из соответствующих приращений Ñgji, Ñai, Ñbi, ÑQi, Ñ ki, а формирование приращений Ñyi осуществляется по той же формуле, что и формирование пространственной суммы ViÑt. Следовательно, для сохранения возможности воспроизведения динамических свойств нейрона в соответствии с (34–36), в алгоритме базового нейронного модуля (БНМ) достаточно иметь лишь одно условие вида
и одно соотношение вида Остальные параметры ЦНП, а именно ai, bi, Qi, k i , можно формировать в цифровых интеграторах синаптических весов путем использования необходимых схемных соединений и введения соответствующих обозначений. Учитывая это обстоятельство, а также то, что в простейшем варианте БНМ должен функционировать как минимум в режиме формального нейрона с выходом Zi +1=Sign[ViÑt] и быть пригодным для создания более сложных нейропроцессоров с динамическим выходом Zi+1 Ñt=max{0, ViÑt}, представим алгоритм БНМ в следующем виде:
Покажем, что относительно Z БНМ, работающий в соответствии с алгоритмом (69), действительно реализует алгоритм формального нейрона. Для этого введем обозначения:
Подставляя обозначения (70) в алгоритм (69), получим
При gji=gj, Ñgji =0i, Qi =Q, ÑQi =0,Ñt=1 и xjiÎ{0, 1} система уравнений (71) принимает вид что с точностью до обозначений совпадает с алгоритмом формального нейрона.
Полагая в некотором БНМ
найдем, что относительно выхода VÑt тот же модуль будет воспроизводить другую систему уравнений: Работающий в соответствии с (72) БНМ назовем модулем пространственной суммации.
Далее учтем, что произведения yi-1Ñt могут формироваться таким же БНМ, если в алгоритме принять и использовать выход ZÑt.
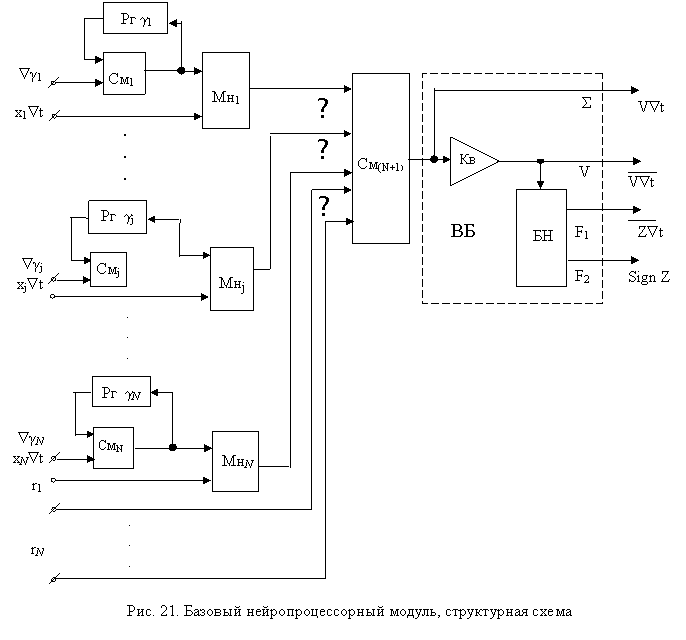
Этот второй, запрограммированный в соответствии с (73) БНМ назовем модулем временной суммации. Реализуемый им алгоритм имеет вид: Если теперь использовать приращения ViÑt=Ñyi из алгоритма (72) модуля пространственной суммации в качестве приращений Ñg1i=Ñyi для алгоритма (74) модуля временной суммации, а также учесть, что в алгоритме (74) из приращений Ñyi формируются величины yi , то на выходе ZÑt БНМ временной суммации получим выходные приращения динамического ЦНП, у которого b=k=1. В дальнейшем с целью упрощения анализа будем полагать, что если не сделаны специальные оговорки, то равенство b=k=1 выполняется автоматически. Таким образом, отдельный БНМ действительно может работать в режиме формального нейрона, пространственного и временного сумматора. Структурная схема такого БНМ показана на рис. 21. Из рисунка видно, что в общем случае модуль содержит N синаптических блоков, каждый из которых состоит из умножителя Мнj , регистра Рг gj синаптического веса g j и двухвходового сумматора Смj, суммирующего значения весовых коэффициентов gji с их приращениями Ñgji. На первые входы умножителей Мн j поступают входные воздействия xj(i-1)Ñt с выходов других БНМ или от периферийного оборудования, связанного с внешней средой. Произведения gji(xj(i-1)Ñt) суммируются многовходовым пространственным сумматором См(N+1) и в виде результирующей величины ViÑt поступают на выход модуля, а также на вход квантователя Кв.
Следует отметить, что при n–разрядных синаптических весах gji и n–разрядных входных воздействиях xj(i-1)Ñt произведения g ji(xj(i-1)Ñt) и их сумма ViÑt будут содержать 2n двоичных разрядов. Очевидно, что с выхода БНМ эти 2n–разрядные величины могут подаваться лишь на дополнительные входы rj расширения многовходового сумматора См(N+1) в качестве слагаемых и не могут использоваться ни в качестве приращений Ñgji , ни в качестве сомножителей (xj(i-1)Ñt) на входах Мнj. Поэтому для согласования разрядностей величин ViÑt с разрядностью приращений Ñgji и разрядностью входных воздействий xj(i-1)Ñt используется квантователь Кв, реализующий зависимость где ViÑt – квантованные значения ViÑt, содержащее n ее старших разрядов; Oi – остаток квантования, содержащий nмладших разрядов той же суммы ViÑt.
Для уменьшения погрешности квантования величин ViÑt остатки O i при квантовании по алгоритму (75) не отбрасываются, а учитываются в соответствии с алгоритмом где Oi-1 – остаток квантования суммы Vi-1 Ñt в предыдущий (i-1)–й момент времени ti. Учитывая последнее соотношение, а также то, что выходной блок (ВБ) модуля формирует значения выходной функции ZiÑt, переформулируем алгоритм (69) БНМ следующим образом: где gij - n-разрядное значение синаптического веса j-го входа БНМ в i-й момент дискретного времени t; Ñgji – n-разрядное приращение синаптического веса j-го входа; ViÑt – 2n-разрядная неквантованная сумма на выходе сумматора См(N+1) ; xj(i-1)Ñt – n-разрядные приращения входных воздействий; rji – величины, поступающие на входы rj сумматора См(N+1) с выходов ViÑt других нейроподобных модулей; ViÑt – n-разрядные квантованные значения величин ViÑt.
Выходные функции алгоритма (77) формируются выходным блоком ВБ модуля. Этот блок сравнительно прост, и по количеству используемого оборудования (совместно с оборудованием квантователя Кв, работающего по алгоритму (76)) примерно соответствует оборудованию ОБСБ синаптического блока. Иначе говоря, можно считать, что объем оборудования ОББНМ нейроподобного модуля может быть оценен соотношением
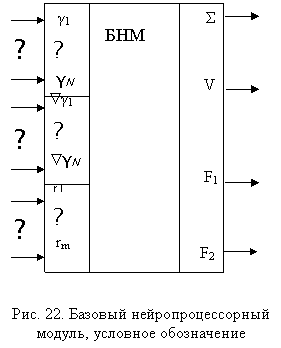
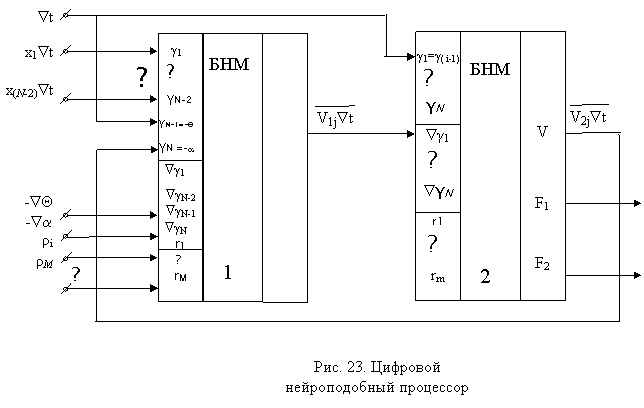
Условное графическое обозначение БНМ показано на рис. 22. Используя данное обозначение, представим схему цифрового нейроподобного процессора так, как это показано на рис. 23. Информационные процессы, протекающие в данной схеме, могут быть описаны следующей системой разностных уравнений: где Q – порог моделируемого воздействия; a – параметр, характеризующий инерционные свойства нервной клетки. Сравнивая уравнения системы (79) с математическим описанием информационных процессов в цифровой модели нейрона, найдем, что относительно выходной функции Zi+1Ñt система (79) действительно совпадает с алгоритмом нейропроцессора динамического типа. Относительно выходной функции Z i+1 отдельный БНМ работает в режиме обычного формального нейрона.
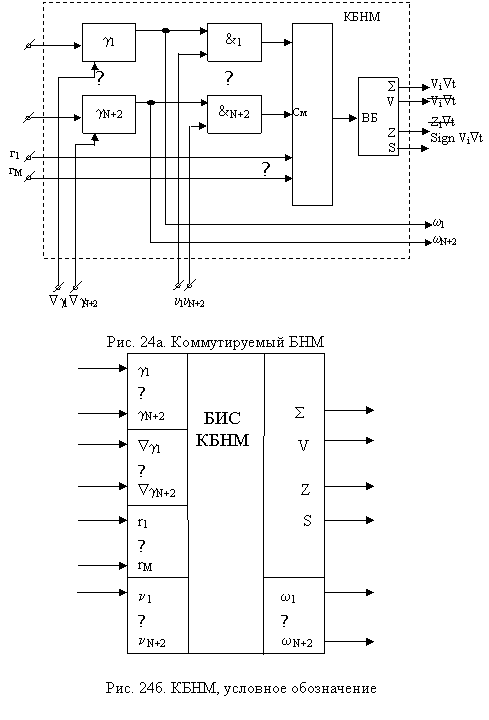
Таким образом, БНМ представляет собой достаточно универсальный модуль, который способен работать в режимах пространственного сумматора и формального нейрона, а также в режиме временного сумматора. Более того, тот же модуль может служить и в качестве расширителя входов пространственного сумматора. Поэтому при его микроэлектронной реализации получается единственная универсальная БИС БНМ, выполняющая функции как БИС1, так и БИС2. Очевидно, что в такой БИС желательно иметь как можно больше синаптических входов, т. е. тех входов, на реализацию которых уходит основная часть оборудования БНМ. Однако, при проектировании БНМ необходимо учитывать и то, что в различных режимах оборудование модуля используется неравномерно. Так, из рис. 23 видно, что в БНМ1, выполняющем функции пространственного сумматора, используется практически все оборудование схемы. В то же время в БНМ2, реализующем функции временного сумматора, используется лишь 2(N+1)-1 –я его часть. При возрастании N эффективность применения модуля БНМ2 уменьшается. С целью устранения данного недостатка описанных базовых нейронных модулей используем идею коммутации их синаптических блоков. При этом появляются модули с внутренней коммутацией. 15. Базовый модуль с внутренней коммутацией Идею построения коммутируемых БНМ (КБНМ) поясним при помощи схемы, показанной на рис. 24а (на рис. 24б показано ее условное графическое обозначение).
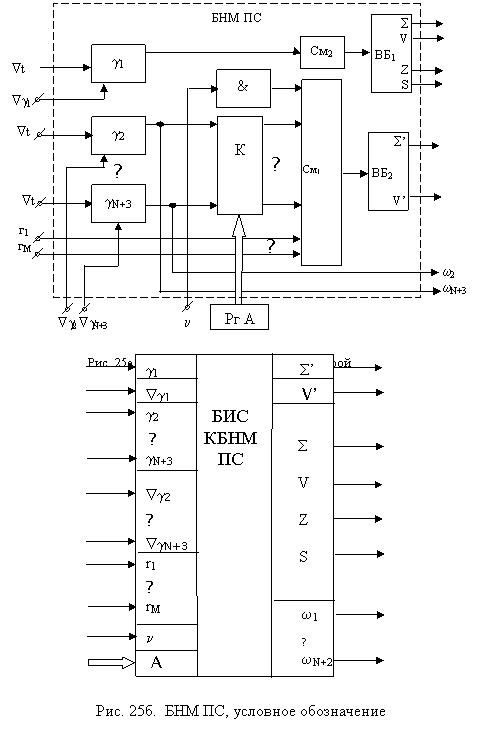
Входы νj (j=1, N+2) являются управляющими. Причем, νj Î{0, 1}. Если некоторый сигнал νj =0, то соответствующий j-й синаптический блок отключается от сумматора и при помощи дополнительного выхода wj может быть подсоединен к некоторому входу расширения r j другого БНМ. Эффективность использования оборудования ЦНП, состоящего из двух коммутируемых БНМ, возрастает почти в два раза. Следующий этап совершенствования структуры БНМ связан с обеспечением возможности построения ЦНП не на двух, а на одном нейроподобном модуле. Достигается это путем обеспечения возможности переключения режимов работы модуля. 16. Базовый модуль с перестраиваемой структурой Блок-схема базового модуля с перестраиваемой структурой (БНМ ПС) имеет вид, показанный на рис. 25а (условное графическое обозначение приведено на рис. 25б). При использовании БИС БНМ ПС схема ЦНП может быть построена на одной микросхеме путем коммутации ее входов и выходов (рис. 26).
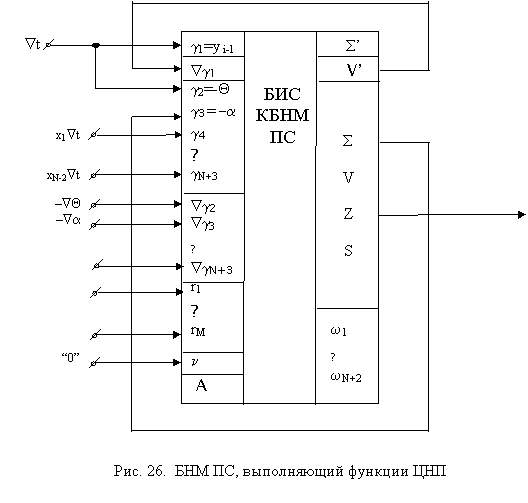
Полюсы r1¸ rM позволяют увеличивать число входов ЦНП до нужного числа. В качестве расширителей входов используются такие же БИС. (Выходы S, S’, w1¸wN+2). При n=1 и отсутствии обратных связей БНМ ПС является обучаемым формальным нейроном или расширителем входов ЦНП. С показанными на рис. 26 обратными связями та же БИС выполняет функции ЦНП.
Подключение такой же БИС на входы расширения позволяют увеличить число входов ЦНП. Таким образом, рассмотренный базовый модуль является полифункциональным и, кроме того, позволяет повышать эффективность использования своего оборудования путем переключения синаптических блоков. Достигается это путем незначительных аппаратных затрат внутри модуля и использования дополнительных управляющих, входных и выходных линий. 17. Расчет экономического эффекта Расчет экономического эффекта от производства новой продукции, не имеющей базы сравнения (принципиально новой продукции), осуществляется исходя из прибыли реализации единицы этой продукции, удельных капитальных вложений с учетом нормативного коэффициента их эффективности и годового объема производства принципиально новой продукции: Э = ( П – Ен*К)*А2 (80) где Э – годовой экономический эффект от производства нового продукта, руб.; П – прибыль от реализации единицы нового продукта, руб.; Ен – нормативный коэффициент эффективности капитальных вложений, равный 1,5; К – удельные капитальные вложения в производство нового продукта, руб.; А2 – годовой объем производства новых продуктов, ед. Для выбора наиболее экономичного варианта производства производятся расчеты сравнительной экономической эффективности на основе определения минимума приведенных задач: Зi = Сi + Ен*Кi ³ min (81) где Зi – удельные (на единицу продукции) приведенные затраты на производство продукта, руб.; Сi – удельные текущие затраты (себестоимость) на производство продукта, руб.; Кi – удельные капитальные вложения в продукт, руб. Расчеты по формуле (81) позволяют из всего множества вариантов выпуска одинаковых по объему и качеству продуктов при различных текущих затратах и капитальных вложений выбрать вариант с наименьшими совокупными затратами. Решение о выборе варианта для постановки его на производство формируется на основе анализа экономической эффективности и народнохозяйственного значения продукта при его использовании с учетом расчетов, выполненных по формуле (81). Заключение Изложенный материал отражает один из важных подходов к проектированию искусственных нейронов и нейронных сетей. Суть этого подхода состоит в синтезе и аппаратной реализации разностных алгоритмов обработки информации в нервных клетках, воспроизводящих как моделирующие, так и вычислительные свойства нейронов. Данное обстоятельство оправдывает использование для обозначения синтезированного цифрового динамического нейроподобного элемента термина «цифровой нейропроцессор». Особенность такого ЦНП заключается в том, что, помимо выполнения крупных математических операций, он структурно настраивается на выполнение крупных моделирующих операторов типа формального нейрона, адаптивного нейрона и т. д. Нейронные операторы позволяют использовать ЦНП для имитационного моделирования неформализованных нейросетевых процессов в мозге. Математические операции позволяют создавать обучаемые сети систем распознавания образов. Более того, эти операции позволяют строить нейропроцессорные сети для решения таких задач вычислительной математики, как решение систем линейных алгебраических уравнений с произвольной, в том числе прямоугольной и квадратной особенной матрицей коэффициентов; решение задач линейного программирования; решение систем дифференциальных уравнений со сложными граничными условиями, решение интегральных уравнений и т. п. В то же время следует отметить, что данный подход не является единственным. В настоящее время многие фирмы США, Японии, Европы ведут интенсивные исследования, направленные на создание нейрокомпьютеров и нейроэлементов различных модификаций. Прежде всего это касается симуляционных (моделирующих) нейрокомпьютеров, разрабатываемых в виде пакетов прикладных программ для персональных ЭВМ и суперЭВМ. Разрабатываются нейроЭВМ на новой технологической основе, например оптической, оптоэлектронной, молекулярной. Литература 1. Чернухин Ю. В. Нейропроцессоры. Таганрог, ТРТИ, 1994. 2. Чернухин Ю. В. Искусственный интеллект и нейрокомпьютеры. Таганрог, ТРТИ, 1997. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2010 |
|