|
|
|
|
Диплом: Дифференциальные уравнения с разрывной правой частью
Диплом: Дифференциальные уравнения с разрывной правой частью
Содержание. Глава I
Введение.
2
§1. Актуальность темы. 2
§2. Обзор работ. 6
Глава II
Определения решения дифференциального уравнения с разрывной правой частью.
8
§1. Обоснование необходимости обобщения понятия
решения. 8
§2. Определения решения. 10
Глава III
Исследование устойчивости для дифференциальных
уравнений с разрывными правыми частями. 23
§1. Определение устойчивости. Метод функций Ляпунова. 23
§2. Некоторые сведения теории дифференциальных
уравнений с импульсным воздействием. 27
§3. Связь рассматриваемых теорий. 31
Заключение.
34
Литература.
35
Глава I
Введение.
§1. Актуальность темы.
Актуальность данной темы в значительной степени обусловлена многочисленными
приложениями теории дифференциальных уравнений с разрывными правыми частями.
Ряд процессов в механике, электротехнике и в других областях характеризуются
тем, что правые части дифференциальных уравнений, которые описывают их
динамику, претерпевают разрывы в зависимости от текущего состояния процесса.
Стандартный пример такой динамической системы – механическая система с сухим
трением, когда сила сопротивления может принимать одно из двух двух
противоположных по знаку значений в зависимости от направления движения.
Рассмотрим эту систему подробнее.
Механическая система с сухим трением.
Как показано в [3] можно установить зависимость между работой, затраченной на
преодоление сил трения и скоростью движения. Эта зависимость получается
совершенно различной для случая движения груза массы m в жидкости и
трения о какую-либо твердую поверхность. В первом случае (случай “жидкого
трения”) работа существенно зависит от скорости и при уменьшении скорости
уменьшается и может быть сделана как угодно малой. Во втором случае (случай
“сухого трения”), наоборот, работа мало зависит от скорости, и как бы медленно
ни двигали груз, необходимо затратить на его перемещение некоторую конечную и
вполне определенную работу, т.е. сила трения даже при сколь угодно малой
скорости имеет конечную величину. Кроме этого, учитывая, что сила трения всегда
направлена в сторону, противоположную скорости, и, значит при переходе через
нуль сила трения меняет знак на обратный, в случае “жидкого трения” получаем,
что сила трения без скачка проходит через нуль и меняет при этом знак:
В случае же “сухого трения” при скорости, стремящейся к нулю, сила трения с
двух сторон стремится к разным конечным пределам (в частности противоположным
по знаку, но одинаковым по абсолютной величине), т.е. при нуле претерпевает
разрыв:
Т.о. математические модели механических систем с кулоновым трением,
полученные в рамках механики систем абсолютно твердых тел, представляют собой
дифференциальные уравнения, правые части которых являются функциями,
разрывными относительно обобщенных скоростей (сила трения изменяется
скачкообразно при изменении направления движения).
Ситуация, подобная вышеописанной, особенно часто возникает в системах
автоматического управления: стремление повысить быстродействие системы,
минимизировать энергетические затраты на управление, ограничить область
возможных изменений регулируемых параметров и т.п. приводит к управляющим
воздействиям в виде разрывных функций. В частности, такими системами
автоматического управления являются системы с переменной стуктурой и со
скользящими режимами.
Системы с переменной структурой и со скользящим режимом.
Исследование этих систем в большинстве случаев осуществляется на основе
развитого в работе [3] метода фазового пространства. Согласно этому методу,
состояние динамической системы 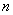 –го порядка в любой момент времени полностью определяется значениями
–го порядка в любой момент времени полностью определяется значениями 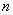 координат. Значения этих координат задают некоторую точку в
координат. Значения этих координат задают некоторую точку в 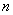 –мерном пространстве, по осям которого отложены координаты системы. Т.о.,
каждому новому состоянию системы соответствуют все новые и новые точки
пространства и изменению состояний системы можно соподчинить движение некоторой
точки, которая называется изображающей точкой, а пространство – фазовым
пространством. При движении системы ее координаты изменяются. И изображающая
точка описывает некоторую кривую (выражающую для данного движения зависимость
скорости от координат), которая называется фазовой траекторией. По виду этих
траекторий можно судить о свойствах рассматриваемой динамической системы, и,
более того, изменять их, деформируя фазовые траектории при соответствующем
выборе управляющих воздействий. Движение изображающей точки характеризуется
вектором фазовой скорости, который направлен по касательной к траектории в
сторону движения.
Определение систем с переменной структурой дано в работе [13]. Под системами
с переменной структурой авторы понимают системы, в которых связи между
функциональными элементами меняются тем или иным образом, в отличие от систем
с фиксированной структурой, в которых совокупность функциональных элементов и
характер связей между ними остаются неизменными.
Одним из режимов работы таких систем является скользящий режим,
характеризуемый бесконечной частотой переключения функции управления.
Скользящий режим возникает, если в окрестности поверхности, на которой
функция управления претерпевает разрывы, фазовые траектории направлены
навстречу друг другу
–мерном пространстве, по осям которого отложены координаты системы. Т.о.,
каждому новому состоянию системы соответствуют все новые и новые точки
пространства и изменению состояний системы можно соподчинить движение некоторой
точки, которая называется изображающей точкой, а пространство – фазовым
пространством. При движении системы ее координаты изменяются. И изображающая
точка описывает некоторую кривую (выражающую для данного движения зависимость
скорости от координат), которая называется фазовой траекторией. По виду этих
траекторий можно судить о свойствах рассматриваемой динамической системы, и,
более того, изменять их, деформируя фазовые траектории при соответствующем
выборе управляющих воздействий. Движение изображающей точки характеризуется
вектором фазовой скорости, который направлен по касательной к траектории в
сторону движения.
Определение систем с переменной структурой дано в работе [13]. Под системами
с переменной структурой авторы понимают системы, в которых связи между
функциональными элементами меняются тем или иным образом, в отличие от систем
с фиксированной структурой, в которых совокупность функциональных элементов и
характер связей между ними остаются неизменными.
Одним из режимов работы таких систем является скользящий режим,
характеризуемый бесконечной частотой переключения функции управления.
Скользящий режим возникает, если в окрестности поверхности, на которой
функция управления претерпевает разрывы, фазовые траектории направлены
навстречу друг другу
 После попадания на поверхность разрыва изображающая точка не может в течение
любого даже сколь угодно малого, но конечного интервала времени двигаться по
любой из траекторий, примыкающих к этой поверхности (при любом смещении
всегда возникает движение, возвращающее изображающую точку на поверхность
разрыва).
В [7] рассматривается еще случай, когда решение наоборот не может попасть на
соответствующий участок поверхности разрыва (при возрастании времени):
Скользящие режимы обладают рядом привлекательных свойств с т.з. построения
систем автоматического управления (часто скользящие режимы специально вводят
в системы). Одна из особенностей, связанная с независимостью их от
характеристик управляемого объекта и возможностью наделить их желаемыми
свойствами, и обуславливает широкое применение скользящих движений.
Т.о., существование теории релейных систем, систем переменной структуры,
реализация законов оптимального управления, механики, электротехники приводят
к необходимости изучения общей теории диф. уравн. с разрывными правыми
частями, для которых в общем случае неприемлемы методы классической теории
дифференциальных уравнений.
§2. Обзор работ по теории дифференциальных уравнений с разрывными правыми
частями.
Различным вопросам этой теории посвящены отдельные параграфы и главы в книгах
[3,4,7,9], а также большое число журнальных статей.
Систематическое изложение этой теории имеется в статьях А.Ф. Филиппова. В
[16] Филиппов рассмотрел диф. уравн. с однозначными разрывными правыми
частями, ввел понятие решения и доказал основные теоремы качественной теории.
Различные направления исследования релейных диф. уравн.
После попадания на поверхность разрыва изображающая точка не может в течение
любого даже сколь угодно малого, но конечного интервала времени двигаться по
любой из траекторий, примыкающих к этой поверхности (при любом смещении
всегда возникает движение, возвращающее изображающую точку на поверхность
разрыва).
В [7] рассматривается еще случай, когда решение наоборот не может попасть на
соответствующий участок поверхности разрыва (при возрастании времени):
Скользящие режимы обладают рядом привлекательных свойств с т.з. построения
систем автоматического управления (часто скользящие режимы специально вводят
в системы). Одна из особенностей, связанная с независимостью их от
характеристик управляемого объекта и возможностью наделить их желаемыми
свойствами, и обуславливает широкое применение скользящих движений.
Т.о., существование теории релейных систем, систем переменной структуры,
реализация законов оптимального управления, механики, электротехники приводят
к необходимости изучения общей теории диф. уравн. с разрывными правыми
частями, для которых в общем случае неприемлемы методы классической теории
дифференциальных уравнений.
§2. Обзор работ по теории дифференциальных уравнений с разрывными правыми
частями.
Различным вопросам этой теории посвящены отдельные параграфы и главы в книгах
[3,4,7,9], а также большое число журнальных статей.
Систематическое изложение этой теории имеется в статьях А.Ф. Филиппова. В
[16] Филиппов рассмотрел диф. уравн. с однозначными разрывными правыми
частями, ввел понятие решения и доказал основные теоремы качественной теории.
Различные направления исследования релейных диф. уравн. 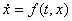 , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x
функций рассмотрены в статье [5].
Теория систем автоматического управления, описываемых дифференциальными
уравнениями с разрывными правыми частями рассматривается в книгах [13, 14,
15]. В работе С.В. Емельянова [13] излагается один из разделов теории
автоматичесеого управления – теория систем с переменной структурой,
принадлежащих к классу нелинейных систем автоматического регулирования, в
которых широко используются скользящие режимы. Скользящие режимы релейных
систем изучались Ю.И Неймарком [10], Ю.И. Алимовым [2] и др. Но появление
систем с переменной структурой породило интерес к теории скользящих режимов
не только в релейных системах общего вида [14, 15]. Содержание последних
книг составляют проблемы, связанные с исследованием систем с разрывными
управляющими воздействиями, в [14] приводится математический аппарат для
исследования разрывных динамических систем, которые не рассматриваются в
классической теории диф. уравнений. Обзор и основные направления теории диф.
уравнений с разрвными правыми частями приводятся в книге [17], которая
явилась основной при написании дипломной работы.
Во всех вышеперечисленных работах теория разрывных систем основывается на
теории дифференциальных включений. Нами было сделано предположение, что эти
системы можно свести к системам дифференциальных уравнений с импульсным
воздействием, теория которых изложена в [12]. Для этого потребуется дать
определения решения, устойчивости решения разрывной системы в смысле системы
с импульсным воздействием, сформулировать теорему об устойчивости нулевого
решения.
Глава II
Определения решения дифференциального уравнения с разрывной правой частью.
Здесь из лагаются различные определения решений дифференциальных уравнений с
разрывными правыми частями, устанавливается связь таких уравнений с
дифференциальными включениями, указываются условия их применимости.
§1. Обоснование необходимости обобщения понятия
решения дифференциального уравнения.
, т.е. таких уравнений, у которых правая часть не является ненпрерывной по x
функций рассмотрены в статье [5].
Теория систем автоматического управления, описываемых дифференциальными
уравнениями с разрывными правыми частями рассматривается в книгах [13, 14,
15]. В работе С.В. Емельянова [13] излагается один из разделов теории
автоматичесеого управления – теория систем с переменной структурой,
принадлежащих к классу нелинейных систем автоматического регулирования, в
которых широко используются скользящие режимы. Скользящие режимы релейных
систем изучались Ю.И Неймарком [10], Ю.И. Алимовым [2] и др. Но появление
систем с переменной структурой породило интерес к теории скользящих режимов
не только в релейных системах общего вида [14, 15]. Содержание последних
книг составляют проблемы, связанные с исследованием систем с разрывными
управляющими воздействиями, в [14] приводится математический аппарат для
исследования разрывных динамических систем, которые не рассматриваются в
классической теории диф. уравнений. Обзор и основные направления теории диф.
уравнений с разрвными правыми частями приводятся в книге [17], которая
явилась основной при написании дипломной работы.
Во всех вышеперечисленных работах теория разрывных систем основывается на
теории дифференциальных включений. Нами было сделано предположение, что эти
системы можно свести к системам дифференциальных уравнений с импульсным
воздействием, теория которых изложена в [12]. Для этого потребуется дать
определения решения, устойчивости решения разрывной системы в смысле системы
с импульсным воздействием, сформулировать теорему об устойчивости нулевого
решения.
Глава II
Определения решения дифференциального уравнения с разрывной правой частью.
Здесь из лагаются различные определения решений дифференциальных уравнений с
разрывными правыми частями, устанавливается связь таких уравнений с
дифференциальными включениями, указываются условия их применимости.
§1. Обоснование необходимости обобщения понятия
решения дифференциального уравнения.
Определение1. Решением дифференциального уравнения 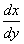 =
= 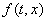
с непрерывной правой частью называется функция 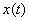 , которая всюду на данном интервале имеет производную и удовлетворяет этому
уравнению.
, которая всюду на данном интервале имеет производную и удовлетворяет этому
уравнению. Для дифференциальных уравнений с разрывными правыми
частями такое определение непригодно, как показывают следующие примеры.
Пример 1.
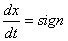 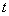 При
При 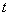 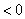 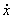 =-1 и решение выражается формулой =-1 и решение выражается формулой 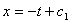 ; ;
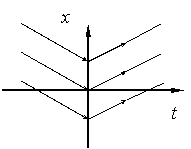 при при 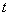 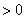 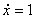 , решение , решение 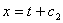 : :
Исходя из требования непрерывности решения при 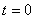 :
x(0)= :
x(0)=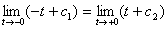 , ,
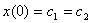 . Поэтому решение выражается формулой . Поэтому решение выражается формулой 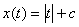 . При . При 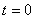 производной производной 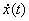 не существует.
Пример 2. не существует.
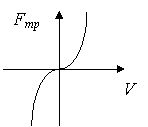
Пример 2.
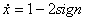 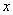 При
При 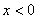 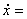 3, решение 3, решение 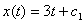 ,
при ,
при 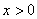 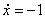 , решение , решение 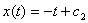 : :
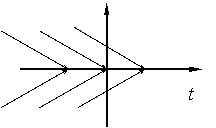 x
При возрастании x
При возрастании 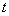 каждое решение доходит до прямой
каждое решение доходит до прямой 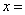 0. Поле направлений не позволяет решению сойти с прямой
0. Поле направлений не позволяет решению сойти с прямой 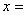 0 ни вверх, ни вниз. Если же продолжить решение по этой прямой, то получаемая
функция
0 ни вверх, ни вниз. Если же продолжить решение по этой прямой, то получаемая
функция 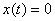 не
удовлетворяет уравнению в обычном смысле, т.к. для нее не
удовлетворяет уравнению в обычном смысле, т.к. для нее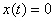 , а правая часть уравнения при
, а правая часть уравнения при 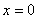 равна 1-sign 0=1
равна 1-sign 0=1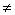 0.
Кроме этого, уравнение с непрерывной правой частью равносильно интегральному
уравнению
0.
Кроме этого, уравнение с непрерывной правой частью равносильно интегральному
уравнению
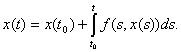 В случае, когда f(t,x) разрывна по t и непрерывна по x
(пример 1), решением уравнения можно назвать функции, удовлетворяющие
интегральному уравнению. В этом случае, решения с одной стороны от S
подходят к S, а с другой стороны сходят с S (траектории
“прошивают” поверхность):
S
Решение x(t) попадающее при
В случае, когда f(t,x) разрывна по t и непрерывна по x
(пример 1), решением уравнения можно назвать функции, удовлетворяющие
интегральному уравнению. В этом случае, решения с одной стороны от S
подходят к S, а с другой стороны сходят с S (траектории
“прошивают” поверхность):
S
Решение x(t) попадающее при 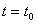 на поверхность разрыва S, продолжается однозначно на значения
на поверхность разрыва S, продолжается однозначно на значения 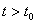 и близкие к
и близкие к 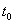 ;
пересекая S решение удовлетворяет уравнению всюду, кроме точки
пересечения, в которой решение не имеет производной (в первом примере S
– это прямая t=0).
В другом случае, когда с обеих сторон поверхности разрыва S решения
приближаются к S (траектории “стыкуются” – скользящий режим), это
определение решения непригодно, т.к. ничего не говорит о том, как продолжится
решение, попавшее на S (пример 2).
Необходимо поэтому было дать такое определение решения, которое охватило бы
эти два основных случая и формулировалось бы независимо от расположения линий
и поверхностей разрыва.
§2. Определения решения.
Рассмотрим уравнение или систему в векторной записи ;
пересекая S решение удовлетворяет уравнению всюду, кроме точки
пересечения, в которой решение не имеет производной (в первом примере S
– это прямая t=0).
В другом случае, когда с обеих сторон поверхности разрыва S решения
приближаются к S (траектории “стыкуются” – скользящий режим), это
определение решения непригодно, т.к. ничего не говорит о том, как продолжится
решение, попавшее на S (пример 2).
Необходимо поэтому было дать такое определение решения, которое охватило бы
эти два основных случая и формулировалось бы независимо от расположения линий
и поверхностей разрыва.
§2. Определения решения.
Рассмотрим уравнение или систему в векторной записи
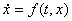 , (1)
с кусочно-непрерывной функцией f в области G; , (1)
с кусочно-непрерывной функцией f в области G;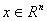 ,
, 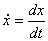 , M –
множество (меры нуль) точек разрыва функции f.
Большинство известных определений решения уравнения (1) могут быть изложены
следующим образом. Для каждой точки , M –
множество (меры нуль) точек разрыва функции f.
Большинство известных определений решения уравнения (1) могут быть изложены
следующим образом. Для каждой точки 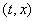 области G указывается множество
области G указывается множество 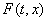 в n-мерном пространстве. Если в точке (t,x) функция f
непрерывна, то множество
в n-мерном пространстве. Если в точке (t,x) функция f
непрерывна, то множество 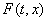 состоит из одной точки, совпадающей со значением функции f в этой точке.
Если же
состоит из одной точки, совпадающей со значением функции f в этой точке.
Если же 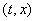 -точка
разрыва функции f, то множество -точка
разрыва функции f, то множество 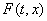 задается тем или иным способом.
задается тем или иным способом.
Определение2. Решением уравнения (1) называется решение
дифференциального включения 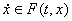 , (2)
, (2)
т.е.
абсолютно непрерывная вектор-функция x(t), определенная на интервале
или отрезке I, для которого почти всюду на I 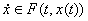 .
.
Другими словами, решение дифференциального уравнения (1) определяется как
функция, у которой производная 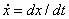 может принимать любые значения из некоторого множества
может принимать любые значения из некоторого множества 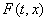 .
Иногда (2) называют диф. уравнением с многозначной правой частью. Функцию
.
Иногда (2) называют диф. уравнением с многозначной правой частью. Функцию 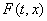 называют многозначной функцией, подчеркивая, что значение
называют многозначной функцией, подчеркивая, что значение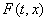 - множество. Если для всех (t, x) множество
- множество. Если для всех (t, x) множество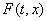 состоит из единственной точки, то (2) – обычное диф. уравнение. Функция
состоит из единственной точки, то (2) – обычное диф. уравнение. Функция 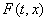 называется однозначной в точке
называется однозначной в точке 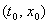 , если множество F
, если множество F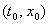 состоит из единственной точки.
Одним из наиболее популярных определений решения разрывной системы является
определение А.Ф. Филиппова.
А. Выпуклое доопределение.
Применимо, в частности, к системам с малым запаздыванием того или иного рода,
а также к некоторым системам с сухим трением.
Для каждой точки
состоит из единственной точки.
Одним из наиболее популярных определений решения разрывной системы является
определение А.Ф. Филиппова.
А. Выпуклое доопределение.
Применимо, в частности, к системам с малым запаздыванием того или иного рода,
а также к некоторым системам с сухим трением.
Для каждой точки 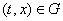 пусть
пусть 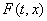 - наименьшее
выпуклое замкнутое множество, содержащее все предельные значения вектор-функции - наименьшее
выпуклое замкнутое множество, содержащее все предельные значения вектор-функции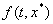 , когда
, когда 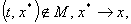 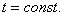 Решением уравнения (1) называется решение включения (2) с только что построенным
Решением уравнения (1) называется решение включения (2) с только что построенным  . Т.к.
. Т.к. 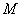 - множество
меры нуль, то при почти всех - множество
меры нуль, то при почти всех 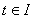 мера сечения множества
мера сечения множества 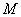 плоскостью
плоскостью 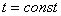 равна
нулю. При таких равна
нулю. При таких 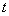 множество
множество 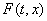 определено для всех
определено для всех 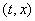 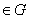 . В точках непрерывности функции
. В точках непрерывности функции 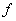 множество
множество 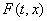 состоит
из одной точки состоит
из одной точки 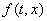 и
решение удовлетворяет уравнению (1) в обычном смысле. Если же точка и
решение удовлетворяет уравнению (1) в обычном смысле. Если же точка 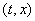 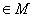 лежит на границах сечений двух или нескольких областей
лежит на границах сечений двух или нескольких областей 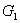 , .,
, ., 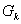 плоскостью плоскостью 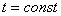 , то множество
, то множество 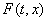 есть
отрезок, выпуклый многоугольник или многогранник с вершинами есть
отрезок, выпуклый многоугольник или многогранник с вершинами 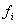 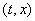 ,
, 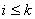 , где , где
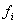 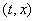 = =  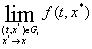 .
Все точки .
Все точки 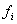 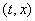 (
(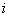 = 1, . , = 1, . , 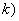 содержатся в
содержатся в 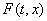 , но не
обязательно, чтобы все они являлись вершинами.
Определение 3.
Вектор-функция , но не
обязательно, чтобы все они являлись вершинами.
Определение 3.
Вектор-функция 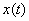 ,
определенная на интервале ,
определенная на интервале 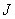 называется решением уравнения (1), если она абсолютно непрерывна и если при
почти всех
называется решением уравнения (1), если она абсолютно непрерывна и если при
почти всех 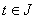 для
любого для
любого 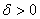 вектор вектор 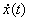 принадлежит наименьшему выпуклому замкнутому множеству (
принадлежит наименьшему выпуклому замкнутому множеству (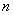 -мерного пространства), содержащему все значения вектор-функции
-мерного пространства), содержащему все значения вектор-функции 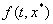 , когда
, когда 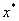 пробегает
почти всю пробегает
почти всю 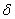 -окрестность точки
-окрестность точки 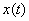 в пространстве X (при фиксированном
в пространстве X (при фиксированном 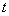 ), т.е. всю окрестность, кроме множества мера нуль.
Такое определение дает однозначное продолжение решения по поверхности разрыва.
Рассмотрим случай, когда функция
), т.е. всю окрестность, кроме множества мера нуль.
Такое определение дает однозначное продолжение решения по поверхности разрыва.
Рассмотрим случай, когда функция 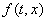 разрывна на гладкой поверхности
разрывна на гладкой поверхности 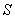 , задаваемой уравнением
, задаваемой уравнением 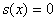 . Поверхность S делит свою окрестность в пространстве на области
. Поверхность S делит свою окрестность в пространстве на области 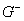 и
и 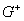 . Пусть при . Пусть при 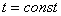 и приближении
и приближении 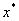 к к 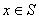 из областей
из областей 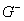 и и 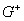 функция имеет предельные значения
функция имеет предельные значения
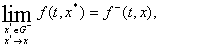 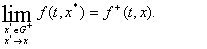 Тогда множество
Тогда множество 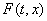 , о
котором говорится в доопределении А, есть отрезок, соединяющий концы векторов , о
котором говорится в доопределении А, есть отрезок, соединяющий концы векторов 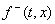 и
и 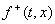 , проведенных из
точки , проведенных из
точки 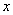 .
aЕсли этот отрезок при .
aЕсли этот отрезок при 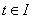 лежит по одну сторону от плоскости
лежит по одну сторону от плоскости 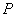 , касательной к поверхности
, касательной к поверхности 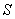 в точке, то решения при этих
в точке, то решения при этих 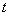 переходят с одной стороны поверхности
переходят с одной стороны поверхности 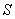 на другую:
на другую:
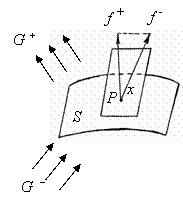 Рис. 1.
aЕсли этот отрезок пересекается с плоскостью
Рис. 1.
aЕсли этот отрезок пересекается с плоскостью 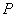 , то точка пересечения является концом вектора
, то точка пересечения является концом вектора 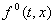 , определяющего скорость движения
, определяющего скорость движения
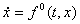 (3)
по поверхности (3)
по поверхности 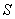 в пространстве в пространстве 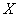 : :
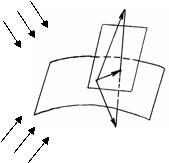 Рис. 2.
Причем касательный вектор к S
Рис. 2.
Причем касательный вектор к S 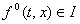 , следовательно
, следовательно 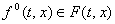 .
Это значит, что функция .
Это значит, что функция 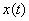 , удовлетворяющая уравнению (3) в силу доопределения А считается решением
уравнения (1). Разумеется, непрерывная функция
, удовлетворяющая уравнению (3) в силу доопределения А считается решением
уравнения (1). Разумеется, непрерывная функция 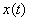 , которая на данной части рассматриваемого интервала времени проходит в области
, которая на данной части рассматриваемого интервала времени проходит в области 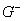 (или в
(или в 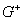 ) и там
удовлетворяет уравнению (1), а на оставшейся части проходит по поверхности ) и там
удовлетворяет уравнению (1), а на оставшейся части проходит по поверхности 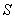 и удовлетворяет уравнению (3), также считается решением уравнения (1) в смысле
доопределения А.
В уравнение (3)
и удовлетворяет уравнению (3), также считается решением уравнения (1) в смысле
доопределения А.
В уравнение (3) 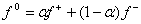 , ,
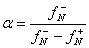 , ( , ( 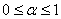 ), ),
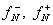 - проекции векторов - проекции векторов 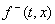 и
и 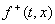 на нормаль к
поверхности на нормаль к
поверхности 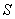 в
точке в
точке 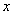 (нормаль
направлена в сторону области (нормаль
направлена в сторону области 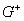 ).
Вместе с тем множество F(t, x) можно было определить иначе. В качестве
) возьмем произвольное ограниченное выпуклое множество, содержащее отрезок
J:
).
Вместе с тем множество F(t, x) можно было определить иначе. В качестве
) возьмем произвольное ограниченное выпуклое множество, содержащее отрезок
J:
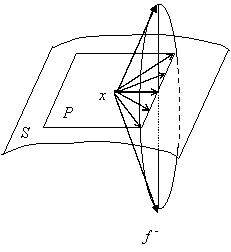 Рис. 3.
При этом на касательной плоскости появляются векторы, отличные от
Рис. 3.
При этом на касательной плоскости появляются векторы, отличные от 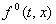 ; это приводит к тому, что кроме решения Филиппова появляются и другие решения.
Т.о. определение (А) А.Ф. Филиппова соответствует минимальному возможному
определению множества F(t, x) среди всех допустимых. Это удобно в том
отношении, что для решения в смысле Филиппова чаще, чем в других случаях, имеет
место единственность решения.
aЕсли весь отрезок с концами
; это приводит к тому, что кроме решения Филиппова появляются и другие решения.
Т.о. определение (А) А.Ф. Филиппова соответствует минимальному возможному
определению множества F(t, x) среди всех допустимых. Это удобно в том
отношении, что для решения в смысле Филиппова чаще, чем в других случаях, имеет
место единственность решения.
aЕсли весь отрезок с концами 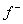 и
и 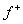 лежит на
плоскости P, то скорость движения лежит на
плоскости P, то скорость движения 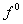 по поверхности разрыва S определяется неоднозначно.
При
по поверхности разрыва S определяется неоднозначно.
При 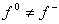 , , 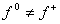 имеет место скользящий режим, о котором шла речь во введение. Пусть уравнение
идеального скольжения имеет вид (3). Вычисляя
имеет место скользящий режим, о котором шла речь во введение. Пусть уравнение
идеального скольжения имеет вид (3). Вычисляя 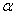 для
для 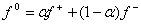 из условия из условия 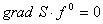 , находим уравнение
, находим уравнение
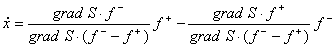 , (4)
с помощью котрого и доопределяется движение в скользящем режиме (начальные
условия для (4) выбираются на поверхности разрыва, т. е. S(x(0))=
0).
Пример 3.
Решить систему , (4)
с помощью котрого и доопределяется движение в скользящем режиме (начальные
условия для (4) выбираются на поверхности разрыва, т. е. S(x(0))=
0).
Пример 3.
Решить систему
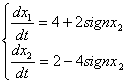 Всякое решение этой системы рано или поздно попадает на прямую
Всякое решение этой системы рано или поздно попадает на прямую 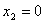 и уже не может сойти с нее. Если точка М лежит на оси
и уже не может сойти с нее. Если точка М лежит на оси 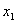 , то в окрестности этой точки вектор
, то в окрестности этой точки вектор 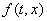 , компоненты которого - правые части системы, принимает два значения:
, компоненты которого - правые части системы, принимает два значения: 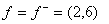 при
при 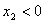 , , 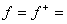 (6,-2) при
(6,-2) при 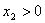 . Отложим
из точки М эти два вектора и соединим их концы отрезком АВ: . Отложим
из точки М эти два вектора и соединим их концы отрезком АВ:
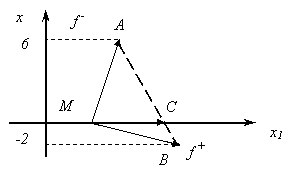 Этот отрезок и будет искомым множеством, в котором, согласно определению 3,
лежит конец вектора
Этот отрезок и будет искомым множеством, в котором, согласно определению 3,
лежит конец вектора 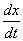 для точки М. В то же время вектор скорости
для точки М. В то же время вектор скорости 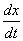 должен лежать на оси
должен лежать на оси 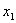 . Т.к. решение не может сойти с нее ни вверх, ни вниз, следовательно, конец
вектора лежит в точке пересечения отрезка АВ и оси
. Т.к. решение не может сойти с нее ни вверх, ни вниз, следовательно, конец
вектора лежит в точке пересечения отрезка АВ и оси 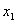 . Т.о., этот вектор определяется однозначно. Легко подсчитать, что
. Т.о., этот вектор определяется однозначно. Легко подсчитать, что 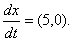 Т.о., связь теорий уравнений (1) с разрывной правой частью с теорией диф.
Включений (2) очевидна. Имея уравнение (1) с разрывной f(t, x)
необходимо заменить значение
Т.о., связь теорий уравнений (1) с разрывной правой частью с теорией диф.
Включений (2) очевидна. Имея уравнение (1) с разрывной f(t, x)
необходимо заменить значение 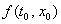 в точке разрыва
в точке разрыва 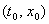 некоторым множеством. Это множество должно быть ограниченным, выпуклым,
замкнутым. Кроме этого оно должно включать все предельные значения
некоторым множеством. Это множество должно быть ограниченным, выпуклым,
замкнутым. Кроме этого оно должно включать все предельные значения 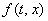 при (t, x)
при (t, x)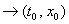 .
После такой замены (для любой точки разрыва) вместо (1) получаем диф. включение
(2), в котором многозначная функция .
После такой замены (для любой точки разрыва) вместо (1) получаем диф. включение
(2), в котором многозначная функция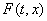 удовлетворяет перечисленным требованиям.
Однако, в некоторых случаях множество
удовлетворяет перечисленным требованиям.
Однако, в некоторых случаях множество 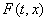 в (2) в точках разрыва функции
в (2) в точках разрыва функции 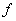 нельзя определить, зная только значения функции
нельзя определить, зная только значения функции 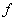 в точках ее непрерывности.
Пример 4.
В механической системе с сухим трением:
в точках ее непрерывности.
Пример 4.
В механической системе с сухим трением:
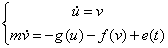 , ,
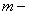 масса тела, масса тела, 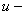 его отклонение,
его отклонение, 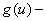 упругая сила,
упругая сила, 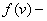 сила
трения, являющаяся нечетной и разрывной при сила
трения, являющаяся нечетной и разрывной при 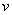 =0 функцией скорости
=0 функцией скорости 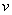 ,
, 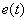 -внешняя сила.
Трение покоя -внешняя сила.
Трение покоя 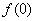 может
принимать любые значения между [d1] своим наибольшим и наименьшим
значениями может
принимать любые значения между [d1] своим наибольшим и наименьшим
значениями 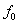 и - и -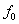 . Если
. Если 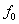 = = 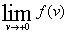 , то применимо доопределение
, то применимо доопределение 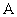 . Если же
. Если же 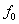 > > 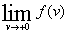 , то движение с нулевой начальной скоростью зависит не только от значений
функции в областях ее непрерывности, но и от величины
, то движение с нулевой начальной скоростью зависит не только от значений
функции в областях ее непрерывности, но и от величины 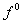 . Доопределение А тогда неприменимо. В обоих случаях систему можно записать в
виде включения (2). Множество
. Доопределение А тогда неприменимо. В обоих случаях систему можно записать в
виде включения (2). Множество 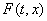 при
при 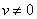 – точка, а при
v=0 – отрезок, длина которого зависит от – точка, а при
v=0 – отрезок, длина которого зависит от 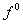 .
Следовательно, множество
.
Следовательно, множество 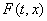 не всегда определяется предельными значениями функции
не всегда определяется предельными значениями функции 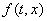 из (1), и в общем случае это множество надо задавать, используя какие-то
сведения о рассматриваемой системе.
Необходимость охватить такие системы приводит к следующему способу построения
множества F(t,x).
Рассмотрим систему
из (1), и в общем случае это множество надо задавать, используя какие-то
сведения о рассматриваемой системе.
Необходимость охватить такие системы приводит к следующему способу построения
множества F(t,x).
Рассмотрим систему
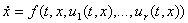 , (6)
где , (6)
где 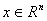 , вектор-функция , вектор-функция 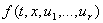 непрерывна по совокупности аргументов, а скалярные или векторные функции
непрерывна по совокупности аргументов, а скалярные или векторные функции 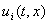 разрывны соответсвенно на множествах
разрывны соответсвенно на множествах 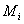 , i=1,.,r, которые могут иметь общие точки и даже совпадать. В каждой
точке (t, x) разрыва функции
, i=1,.,r, которые могут иметь общие точки и даже совпадать. В каждой
точке (t, x) разрыва функции 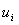 задается замкнутое множество
задается замкнутое множество 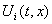 - множество возможных значений аргумента
- множество возможных значений аргумента 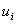 функции
функции 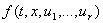 .
Предполагается, что при .
Предполагается, что при 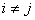 аргументы
аргументы 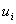 и и 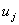 могут независимо друг от друга пробегать соответственно множества
могут независимо друг от друга пробегать соответственно множества 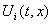 и
и 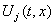 . Обычно, это
условие выполнено, если функции . Обычно, это
условие выполнено, если функции 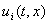 и
и 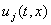 описывают
различные независимые составные части (блоки) физической системы. В точках, где
функция описывают
различные независимые составные части (блоки) физической системы. В точках, где
функция 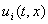 непрерывна, множество
непрерывна, множество 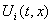 состоит из одной точки
состоит из одной точки 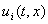 . В точках, разрыва функции
. В точках, разрыва функции 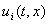 необходимо, чтобы множество
необходимо, чтобы множество 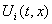 содержало все точки, предельные для точек любой из последовательностей вида
содержало все точки, предельные для точек любой из последовательностей вида 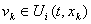 , где
, где 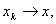 k
=1,2,.(или k
=1,2,.(или 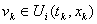 , где , где 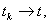 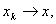 k=1,2,.). Потребуем, чтобы множество
k=1,2,.). Потребуем, чтобы множество 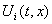 было выпуклым (если
было выпуклым (если 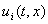 - скалярная функция, то
- скалярная функция, то 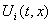 - отрезок или точка).
Пусть
- отрезок или точка).
Пусть
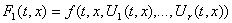 (7) множество значений функции
(7) множество значений функции 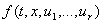 , когда t, x постоянны, а
, когда t, x постоянны, а 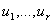 независимо друг от друга пробегают соответственно множества
независимо друг от друга пробегают соответственно множества 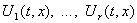 .
Определение 4.
Решением диф. уравн. (6) называют решение диф. включения (2), где
.
Определение 4.
Решением диф. уравн. (6) называют решение диф. включения (2), где 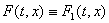 (или
(или 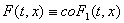 , где , где 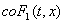 - наименьшее выпуклое множество, содержащее множество
- наименьшее выпуклое множество, содержащее множество 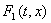 ).
Частными случаями такого способа построения функции F(t,x) является как
доопределение А, так и изложенные ниже Б и В.
Б. Доопределение методом эквивалентного уравнения
(управления).
Применяется к уравнениям вида (6), где f – непрерывная вектор-функция,
).
Частными случаями такого способа построения функции F(t,x) является как
доопределение А, так и изложенные ниже Б и В.
Б. Доопределение методом эквивалентного уравнения
(управления).
Применяется к уравнениям вида (6), где f – непрерывная вектор-функция, 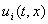 - скалярная функция, разрывная только на гладкой поверхности
- скалярная функция, разрывная только на гладкой поверхности 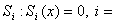 1,., r. Допускоются пересечения и даже совпадения этих поверхностей.
В точках, принадлежащих одной или одновременно нескольким поверхноостям,
например
1,., r. Допускоются пересечения и даже совпадения этих поверхностей.
В точках, принадлежащих одной или одновременно нескольким поверхноостям,
например 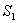 ,., S
m ( ,., S
m (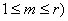 ,
полагают (если решение не может сойти тут же с такой поверхности или с
пересечения этих поверхностей) ,
полагают (если решение не может сойти тут же с такой поверхности или с
пересечения этих поверхностей)
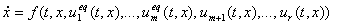 , (8)
где эквивалентные управления , (8)
где эквивалентные управления 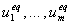 определяются так, чтобы вектор
определяются так, чтобы вектор 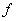 в (8) касался поверхностей
в (8) касался поверхностей 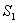 ,., Sm и чтобы значение
,., Sm и чтобы значение 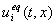 содержалось в отрезке с концами
содержалось в отрезке с концами 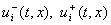 , где
, где 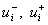 – предельные
значения функции – предельные
значения функции 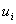 с
обеих сторон поверхности с
обеих сторон поверхности 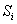 , i=1,., m. Т.о., функции
, i=1,., m. Т.о., функции 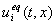 определяются из системы уравнений
определяются из системы уравнений
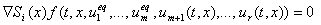 .
Определение 5.
Решением (6) называется абсолютно непрерывная вектор-функция, которая вне
поверхностей .
Определение 5.
Решением (6) называется абсолютно непрерывная вектор-функция, которая вне
поверхностей 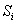 удовлетворяет уравнению (6), а на этих поверхностях и их пересечениях –
уравнениям вида (8) (при почти всех t ).
Например, в случае
удовлетворяет уравнению (6), а на этих поверхностях и их пересечениях –
уравнениям вида (8) (при почти всех t ).
Например, в случае 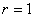 конец вектора
конец вектора 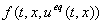 лежит на пересечении касательной к S в точке x с дугой abc
, которую пробегает конец вектора f(t,x,u), когда u изменяется
от
лежит на пересечении касательной к S в точке x с дугой abc
, которую пробегает конец вектора f(t,x,u), когда u изменяется
от 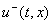 до до 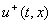 :
Рис. 4.
С геометрической точки зрения, метод эквивалентного управления предполаглет
замену разрывного управления на границе разрыва, где оно не определено,
ненпрерывным управлением, которое направляет вектор скорости в пространстве
состояний системы вдоль пересечения поверхностей разрыва. Например, в системе c
одной поверхностью разрыва
:
Рис. 4.
С геометрической точки зрения, метод эквивалентного управления предполаглет
замену разрывного управления на границе разрыва, где оно не определено,
ненпрерывным управлением, которое направляет вектор скорости в пространстве
состояний системы вдоль пересечения поверхностей разрыва. Например, в системе c
одной поверхностью разрыва 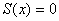 для нахождения этого вектора в некоторой точке (t, x) нужно
построить годограф f(t, x, u), изменяя скалярное управление от
для нахождения этого вектора в некоторой точке (t, x) нужно
построить годограф f(t, x, u), изменяя скалярное управление от 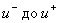 , и найти точку его пересечения с касательной плоскостью. Точка пересечения
определяет
, и найти точку его пересечения с касательной плоскостью. Точка пересечения
определяет 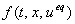 диф.
уравнения (8) (для r=1 (8) примет вид диф.
уравнения (8) (для r=1 (8) примет вид 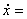 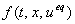 ).
).
© 2010
Частичное или полное использование материалов
запрещено. |
|
|

 После попадания на поверхность разрыва изображающая точка не может в течение
любого даже сколь угодно малого, но конечного интервала времени двигаться по
любой из траекторий, примыкающих к этой поверхности (при любом смещении
всегда возникает движение, возвращающее изображающую точку на поверхность
разрыва).
В [7] рассматривается еще случай, когда решение наоборот не может попасть на
соответствующий участок поверхности разрыва (при возрастании времени):
После попадания на поверхность разрыва изображающая точка не может в течение
любого даже сколь угодно малого, но конечного интервала времени двигаться по
любой из траекторий, примыкающих к этой поверхности (при любом смещении
всегда возникает движение, возвращающее изображающую точку на поверхность
разрыва).
В [7] рассматривается еще случай, когда решение наоборот не может попасть на
соответствующий участок поверхности разрыва (при возрастании времени):

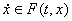 , (2)
, (2)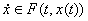 .
. Рис. 1.
aЕсли этот отрезок пересекается с плоскостью
Рис. 1.
aЕсли этот отрезок пересекается с плоскостью  Рис. 2.
Причем касательный вектор к S
Рис. 2.
Причем касательный вектор к S  Рис. 3.
При этом на касательной плоскости появляются векторы, отличные от
Рис. 3.
При этом на касательной плоскости появляются векторы, отличные от 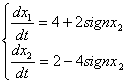 Всякое решение этой системы рано или поздно попадает на прямую
Всякое решение этой системы рано или поздно попадает на прямую  Этот отрезок и будет искомым множеством, в котором, согласно определению 3,
лежит конец вектора
Этот отрезок и будет искомым множеством, в котором, согласно определению 3,
лежит конец вектора 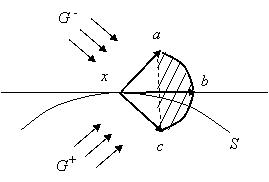



 при
при  x
При возрастании
x
При возрастании 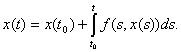 В случае, когда f(t,x) разрывна по t и непрерывна по x
(пример 1), решением уравнения можно назвать функции, удовлетворяющие
интегральному уравнению. В этом случае, решения с одной стороны от S
подходят к S, а с другой стороны сходят с S (траектории
“прошивают” поверхность):
В случае, когда f(t,x) разрывна по t и непрерывна по x
(пример 1), решением уравнения можно назвать функции, удовлетворяющие
интегральному уравнению. В этом случае, решения с одной стороны от S
подходят к S, а с другой стороны сходят с S (траектории
“прошивают” поверхность):
