 |
РУБРИКИ |
Диплом: Дифференциальные уравнения с разрывной правой частью |
РЕКОМЕНДУЕМ |
||
|
Диплом: Дифференциальные уравнения с разрывной правой частью/td> |
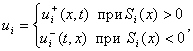 i=1, ., m,
i=1, ., m, 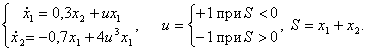 В любой точке прямой разрыва S=0 (т.е. при
В любой точке прямой разрыва S=0 (т.е. при 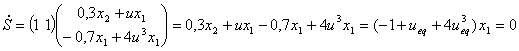 .
Найдем эквивалентное управление из уравнения
.
Найдем эквивалентное управление из уравнения 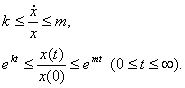 При
При 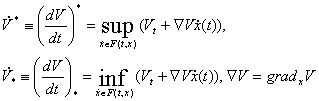 При почти всех t производная
При почти всех t производная  Т.к. на оси Ox имеем
Т.к. на оси Ox имеем 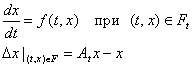 (6)
Т.о., решение системы уравнений (2)
(6)
Т.о., решение системы уравнений (2) 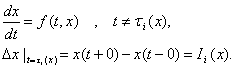 (7)
Устойчивость в системах с нефиксированными моментами
импульсного воздействия.
Определение 2.
Решение x(t) системы уравнений (7), определенное при всех t≥t
0, называется устойчивым по Ляпунову, если для произвольных чисел
(7)
Устойчивость в системах с нефиксированными моментами
импульсного воздействия.
Определение 2.
Решение x(t) системы уравнений (7), определенное при всех t≥t
0, называется устойчивым по Ляпунову, если для произвольных чисел 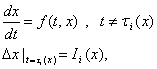 (8)
где
(8)
где 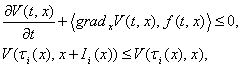 (9)
то тривиальное решение системы уравнений (8) устойчиво.
Если же вместо второго из неравенств (9) потребовать, чтобы выполнялось
неравенство
(9)
то тривиальное решение системы уравнений (8) устойчиво.
Если же вместо второго из неравенств (9) потребовать, чтобы выполнялось
неравенство
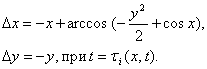 В качестве функции Ляпунова возьмем полную механическую энергию невозмущенного
маятника
В качестве функции Ляпунова возьмем полную механическую энергию невозмущенного
маятника 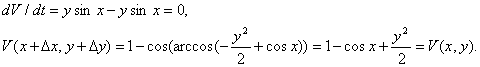 .
Независимо от свойств поверхностей
.
Независимо от свойств поверхностей 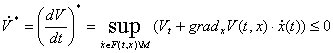 .
При почти всех t производная
.
При почти всех t производная Страницы: 1, 2
|
|
© 2010 |
|
