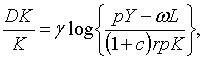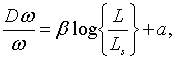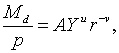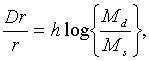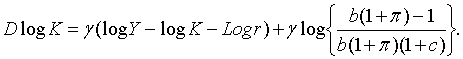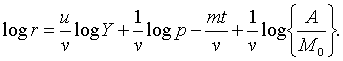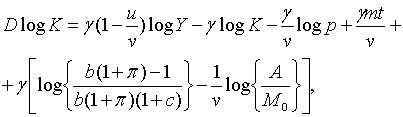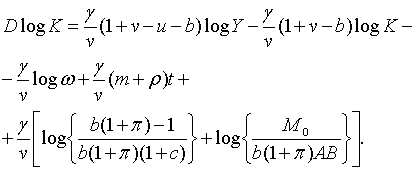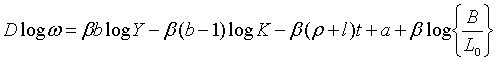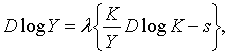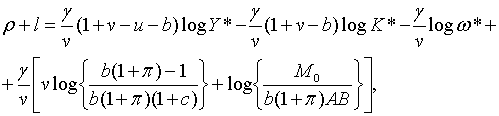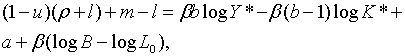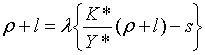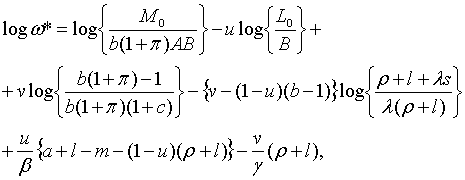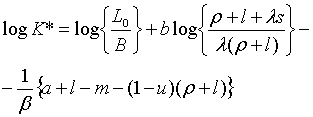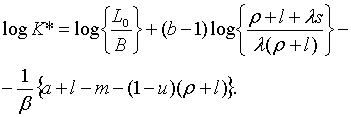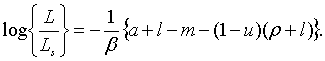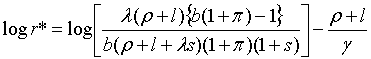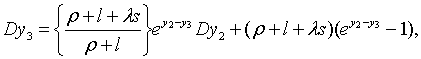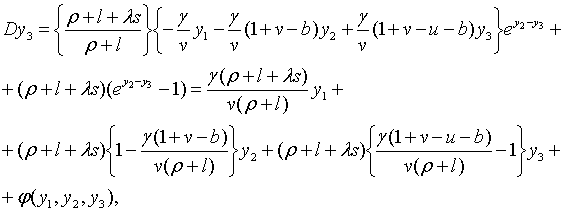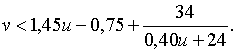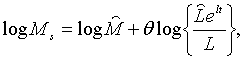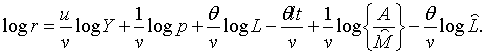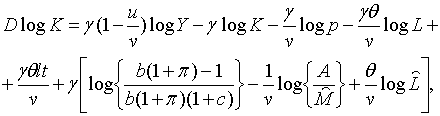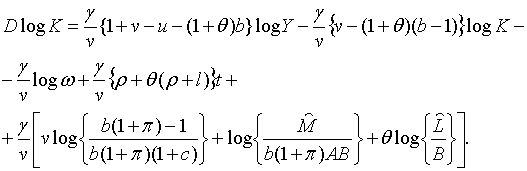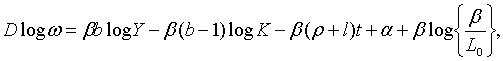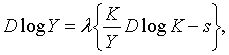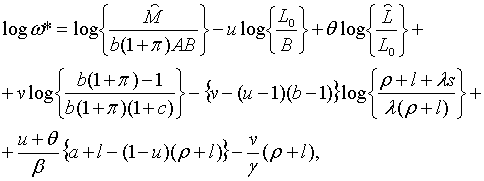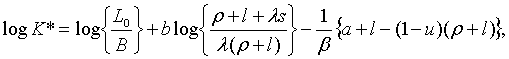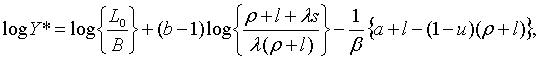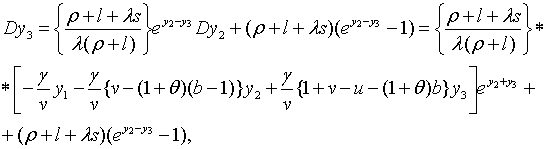|
|
|
|
Курсовая: Математические модели инфляции
Курсовая: Математические модели инфляции
Міністерство Освіти України
Ужгородський державний університет
Математичний факультет
Кваліфікаційна робота
на тему:
МАТЕМАТИЧНІ МОДЕЛІ ІНФЛЯЦІЇ
студента ІV курсу
сп. прикладна математика
Енченко М.В.
Науковий керівник
Головач Й.Г.
Ужгород, 1999
План
Вступ..........................................................................3
Моделі циклічного росту........................................................5
Основна модель.................................................................6
Економічне регулювання........................................................18
Грошова політика.......................................................18
Бюджетна політика......................................................33
Висновки......................................................................45
Вступ
На сучасному етапі Україна знаходиться на шляху ринкових перетворень. Це
зумовлює виникнення багатьох економічних процесів, різним чином впливаючих на
розвиток країни. Одним з таких процесів є інфляція — складне економічне
явище, зміст якого коротко можна висловити так: переповнення каналів обігу
грошовою масою зверх потреб товарообороту. Але, це визначення не можна
рахувати повним, оскількі воно не розкриває ні причин не наслідків інфляції.
Більш точно механізм інфляції можна зрозуміти лише об’єднуючи її з іншими
економічними процесами.
Метою даної роботи є формалізація економічних процесів за допомогою
математичного апарату, для більш точного дослідження механізму інфляції.
В процесі роботи використано багато літературних джерел, як економічних, так
і математичних, які так чи інакше торкаються проблеми побудови математичних
моделей економічних процесів. Розглянута література, в більшості, є
перекладами закордонних видань, так як проблема керування ринковою економікою
вже давно постала перед капіталістичним світом. Основним висновком, який будо
винесено з роботи над літературними джерелами, є те, що інфляцію ні в якому
разі не можна розглядати окремо від інших економічних явищ. Всі процеси в
економіці настількі сильно пов’язані між собою, що розглядати один процес
відірвано від інших неможливо. Одне явище пов’язне з другим, друге – з
третім, і цей умовний ланцюг можна замкнути, тількі описавши економічну
систему в цілому. Саме тому, основна частина роботи присвячується побудові
математичної моделі економіки в цілому, і вже потім досліджується вплив на її
функціонування грошової та бюджетної політики. В модель входять більше двох
десятків параметрів, які визначають економічну коньюктуру. Змінюючи деякі з
них можна дослідити відповідну реакцію економічної системи, яка може
проявлятися у відхиленнях від рівноважних траекторій росту економічних
показників, зміни періодів економічних циклів, виникнення різних явищ,
наприклад інфляції та безробіття. Розглянуто декілька варіантів державної
економічної політики та ефектів від їх використання.
Моделі циклічного росту
Нашою метою є побудова моделі, яка поєднує основні характеристики моделей
економічного циклу і моделей економічного росту при повній зайнятості. Якщо в
моделях економiчного циклу малося на увазі, що траекторія випуску продукції
не залежить від виробничої потужності економіки, то моделі економічного росту
при повній зайнятості засновані на припущенні, що виробничі потужності
народного господарства використовуються в повному об’ємі. Дослідні дані
свідчать, що істина знаходиться десь між цими крайнощами. Існує деякий
механізм зворотного зв’язку, що включає зміни заробітної платні, цін і норм
відсотку, який може на протязі значного періоду часу забезпечити наближену
відповідність між фактичною траекторією випуску продукції і теоретичною
кривою, яка відповідає умові повної зайнятості, хоча і не зберігає
безперервний стан повної зайнятості. В даній роботі вказаний механізм
формально вводиться в модель і грає суттєву роль при синтезі траекторій росту
і економічних циклів.
Отримані в результаті моделі є більш ефективним засобом довгострокового і
корорткострокового прогнозування, ніж моделі економічного циклу і моделі
економічного росту при повній зайнятості.
Перша формальна модель, в якій механізм зворотного зв’язку, яка включає
грошові потоки, грає принципову роль при синтезі траекторій росту і
економічних циклів, була розроблена Філліпсом. Однак ідея самого цього
механізму була видвинута ще Кейнсом. Моделі, які розглядаються нижче
відрізняються від моделі Філліпса тим, що в них входить виробнича функція,
яка допускає взаємозамінність праці і капіталу. В цьому відношенні вони є
розвитком неокласичнох моделі, поєднуючи кейнсіанську і неокласичну теорії.
Основна модель
В цьому розділі буде побудована основна модель. До основної моделі входять
наступні рівняння:
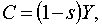
| (1.1) | 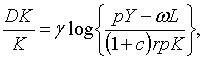
| (1.2) | 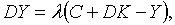
| (1.3) | 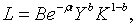
| (1.4) | 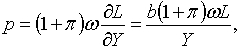
| (1.5) | 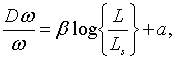
| (1.6) | 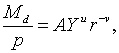
| (1.7) | 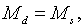
| (1.8) | 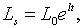
| (1.9) | 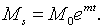
| (1.10) |
В цих рівняннях прийняті слідуючі позначення:
С – реальне споживання,
Y – реальний чистий доход або випуск продукції,
К – об’єм основного капіталу,
L – чисельність використовуємої робочої сили,
Ls – пропозиція робочої сили,
p – рівень цін,
w – ставка заробітної плати,
r – норма процента,
Md – попит на гроші,
Ms – пропозиція грошей,
a, b, c, l, m, s, u, n, b, g, l, p, r, A, B, L0, M0
– додатні константи ( b>1, s<1 ).
Рівняння (1.1) базується на припущенні, що заощадження складають постійну
частку доходу.
Член 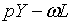 в рівняння
(1.2) рівний прибутку в грошових одиницях, а в рівняння
(1.2) рівний прибутку в грошових одиницях, а 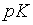 можна розглядувати як вартість основного капіталу в грошових одиницях. Член
можна розглядувати як вартість основного капіталу в грошових одиницях. Член 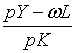 , таким чином, можна рахувати нормою прибутку на основний капітал.
Це рівняння виводиться з припущення, що пропорційний темп росту інвестицій в
основний капітал є зростаюча функція відношення норми прибутку на основний
капітал до норми відсотка. Параметр
, таким чином, можна рахувати нормою прибутку на основний капітал.
Це рівняння виводиться з припущення, що пропорційний темп росту інвестицій в
основний капітал є зростаюча функція відношення норми прибутку на основний
капітал до норми відсотка. Параметр 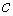 можна рахувати винагородою за ризик.
Розглянемо рівняння (1.3).
можна рахувати винагородою за ризик.
Розглянемо рівняння (1.3). 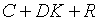 дорівнює загальному сбуту споживчих та капітальних товарів кінцевим споживачам
народного господарства., а
дорівнює загальному сбуту споживчих та капітальних товарів кінцевим споживачам
народного господарства., а 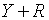 рівне валовому кінцевому продукту. таким чином рівняння (1.3) базується на
припущенні, що темп росту чистого випуску продукції пропорційний перевищенню
сбуту над валовим випуском кінцевої продукції.
рівне валовому кінцевому продукту. таким чином рівняння (1.3) базується на
припущенні, що темп росту чистого випуску продукції пропорційний перевищенню
сбуту над валовим випуском кінцевої продукції.
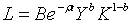 — виробнича функція Кобба-Дугласа.
Рівняння (1.5) базується на припущенні, що рівень цін рівний короткотерміновим
граничним витратам виробництва плюс деяка пропорційна надбавка, яка залежить
від степені відхилення від чистої конкуренції.З рівняння випливає, що рівень
цін дорівнює витратам на оплату праці, розрахованим на одиницю випуску, плюс
пропорційна надбавка — виробнича функція Кобба-Дугласа.
Рівняння (1.5) базується на припущенні, що рівень цін рівний короткотерміновим
граничним витратам виробництва плюс деяка пропорційна надбавка, яка залежить
від степені відхилення від чистої конкуренції.З рівняння випливає, що рівень
цін дорівнює витратам на оплату праці, розрахованим на одиницю випуску, плюс
пропорційна надбавка 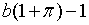 .
Рівняння (1.6) визначає зміну цін на ринку праці. Воно базується на
припушенні, що геометричний темп росту ставки заробітної плати є зростаюча
функція частки використовуємої у виробництві робочої сили. В основі цього
припушення є гіпотеза про те, що, якщо частка використовуємої у виробництві
робочої сили перевищує деякій рівень, конкуренція на ринку праці викликає
підвищення ставки заробітної плати, а якщо частка використовуємої у
виробництві робочої сили менше цього рівня, конкуренція викликає зниження
ставки заробітної плати. Проведене Філліпсом дослідження даних для Англії за
період 1862 – 1957 рр. показує, що на протязі цього періода заробітна плата
мала тенденцію до підвищення або зниження в залежності від того, перевищувала
частка використовуємої у виробництві робочої сили величину 0,95 чи була
менше неї.
Змінна Md в рівнянні (1.7) зображує активи, які фірми та окремі
особи бажають зберегти в грошовій формі (тобто у вигляді готівки чи банківськіх
вкладів). Це рівняня виходить з передумови, що реальний попит на гроші
.
Рівняння (1.6) визначає зміну цін на ринку праці. Воно базується на
припушенні, що геометричний темп росту ставки заробітної плати є зростаюча
функція частки використовуємої у виробництві робочої сили. В основі цього
припушення є гіпотеза про те, що, якщо частка використовуємої у виробництві
робочої сили перевищує деякій рівень, конкуренція на ринку праці викликає
підвищення ставки заробітної плати, а якщо частка використовуємої у
виробництві робочої сили менше цього рівня, конкуренція викликає зниження
ставки заробітної плати. Проведене Філліпсом дослідження даних для Англії за
період 1862 – 1957 рр. показує, що на протязі цього періода заробітна плата
мала тенденцію до підвищення або зниження в залежності від того, перевищувала
частка використовуємої у виробництві робочої сили величину 0,95 чи була
менше неї.
Змінна Md в рівнянні (1.7) зображує активи, які фірми та окремі
особи бажають зберегти в грошовій формі (тобто у вигляді готівки чи банківськіх
вкладів). Це рівняня виходить з передумови, що реальний попит на гроші 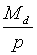 тим більший, чим більший реальний доход і чи нижча норма процента. Кейнс, який
першим вивчив наслідки залежності попиту на гроші від норми відсотка вказав на
дві причини, обумовлюючі цю залежність. Перша з них полягає в тому, що норма
відсотка являє собою витрати на зберігання грошей, а не нерухомості. Друга
причина зводиться до того, що імовірність росту норми відсотка тим більша, чим
нижча його сьогоднішня норма , а якщо очікуваний ріст норми відсотка достатньо
великий, стає більш вигідним відкласти придбання нерухомості (тобто зберігти
гроші), доки очікувана зміна норми відсотка не станеться. Причини, по яким
можно передбачати, що попит на гроші залежить від доходу, набагато очевиднійші.
Зауважимо, зокрема, що попит на гроші пов’язаний з об’ємом очікуємих в
найближчий час платежів, і що сам цей об’єм залежить від доходу.
В рівнянні (1.8) в неявному вигляді містится наступне припущення: норма
відсотка змінюється таким чином, що попит на гроші завжди рівний їх
пропозиції. Це припущення обгрунтовується тим, що якщо попит на гроші
перевищує пропозицію, то необхідність продажу нерухомого майна викличе
падіння цін на нерухомість. Це єквівалентно зростанню норми відсотка, а в
силу (1.7) ріст норми відсотка призведе в кінцевому рахунку до зникнення
надлишку попиту на гроші. Аналогісно, надлишкова пропозиція грошей викликає
зниження норми відсотка, що в свою чергу усуває надлишок пропозиції грошей. В
рівнянні (1.8) передбачається, що ці явища відбуваються миттево. Більш
тверезе припушення, яке легко ввести в модель виражається рівнянням:
тим більший, чим більший реальний доход і чи нижча норма процента. Кейнс, який
першим вивчив наслідки залежності попиту на гроші від норми відсотка вказав на
дві причини, обумовлюючі цю залежність. Перша з них полягає в тому, що норма
відсотка являє собою витрати на зберігання грошей, а не нерухомості. Друга
причина зводиться до того, що імовірність росту норми відсотка тим більша, чим
нижча його сьогоднішня норма , а якщо очікуваний ріст норми відсотка достатньо
великий, стає більш вигідним відкласти придбання нерухомості (тобто зберігти
гроші), доки очікувана зміна норми відсотка не станеться. Причини, по яким
можно передбачати, що попит на гроші залежить від доходу, набагато очевиднійші.
Зауважимо, зокрема, що попит на гроші пов’язаний з об’ємом очікуємих в
найближчий час платежів, і що сам цей об’єм залежить від доходу.
В рівнянні (1.8) в неявному вигляді містится наступне припущення: норма
відсотка змінюється таким чином, що попит на гроші завжди рівний їх
пропозиції. Це припущення обгрунтовується тим, що якщо попит на гроші
перевищує пропозицію, то необхідність продажу нерухомого майна викличе
падіння цін на нерухомість. Це єквівалентно зростанню норми відсотка, а в
силу (1.7) ріст норми відсотка призведе в кінцевому рахунку до зникнення
надлишку попиту на гроші. Аналогісно, надлишкова пропозиція грошей викликає
зниження норми відсотка, що в свою чергу усуває надлишок пропозиції грошей. В
рівнянні (1.8) передбачається, що ці явища відбуваються миттево. Більш
тверезе припушення, яке легко ввести в модель виражається рівнянням:
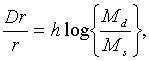
| (1.11) |
де h – додатня константа. Однак, якщо значення h велике порівняно з g, l та
b, то помилка, обумовлена використанням (5.8) замість (1.11), порівняно
невелика. Приймемо для спрошення, що це так і є.
В рівнянні (1.9) передбачається, що пропозиція праці зростає в геометричній
прогрессії, а рівняння (1.10) базується на аналогічному припущенні щодо
пропозиції грошей. Зміст останнього припущення полягає у тому, що грошова
політика нейтральна. Характер реакції системи при зміні пропозиції грошей
внаслідок варіації інших змінних моделі, аналізується в наступному розділі.
Виключаючи 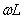 з (1.2) та (1.5), маємо: з (1.2) та (1.5), маємо:
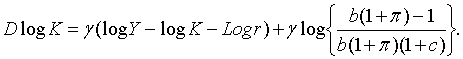
| (1.12) |
Далі, з (1.7), (1.8) та (1.10) отримуємо:
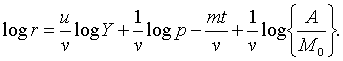
| (1.13) |
З (1.12) та (1.13) випливає
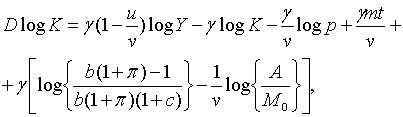
| (1.14) |
що разом з (1.4) та (1.5) дає
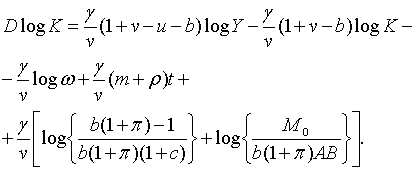
| (1.15) |
З (1.4), (1.6) та (1.9) отримуємо
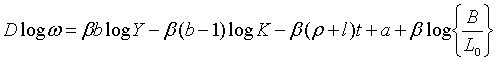
| (1.16) |
а з (1.1) та (1.3) маємо
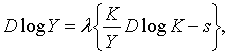
| (1.17) |
Траєкторії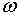 , K
та Y визначаються їх початковими значеннями та системой рівнянь (1.15)
– (1.17). Ця система має частинний розв’язок:
де , K
та Y визначаються їх початковими значеннями та системой рівнянь (1.15)
– (1.17). Ця система має частинний розв’язок:
де 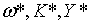 – константи.
Вирази – константи.
Вирази 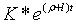 та та 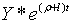 визначають відповідні рівноважні траекторії росту випуска продукції та
капіталу, а вираз
визначають відповідні рівноважні траекторії росту випуска продукції та
капіталу, а вираз 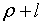 отримав назву темпу рівноважного росту.
Насправді, підставивши значення (1.18) – (1.20) в рівняння (1.15) – (1.17),
отримаємо:
Цим рівнянням задовільняють наступні розв’язки:
Таким чином рівноважний темпи росту
отримав назву темпу рівноважного росту.
Насправді, підставивши значення (1.18) – (1.20) в рівняння (1.15) – (1.17),
отримаємо:
Цим рівнянням задовільняють наступні розв’язки:
Таким чином рівноважний темпи росту 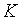 та
та 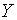 рівний рівний 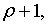 а рівні рівноважних траекторій росту цих змінних тим вищі, чим більша схильність
до заощадження. Цікавою властивістю розглядуємої моделі є підвищеннярівней
рівноважних траекторій росту
а рівні рівноважних траекторій росту цих змінних тим вищі, чим більша схильність
до заощадження. Цікавою властивістю розглядуємої моделі є підвищеннярівней
рівноважних траекторій росту 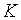 та
та 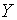 при збільшенні m
— пропорціонального темпа росту пропозиції грошей. Це пояснюється тим, що, коли при збільшенні m
— пропорціонального темпа росту пропозиції грошей. Це пояснюється тим, що, коли 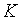 та
та 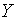 знаходятся на
своїх рівноважних траекторіях росту, частка використовуваної робочої сили є
зростаючою функцією m. Дійсно, виконуючи підстановку з (1.18) у (1.6),
отримаємо: знаходятся на
своїх рівноважних траекторіях росту, частка використовуваної робочої сили є
зростаючою функцією m. Дійсно, виконуючи підстановку з (1.18) у (1.6),
отримаємо:
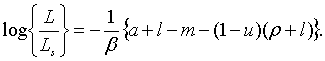
| (1.27) |
Тоді з (1.9) випливає, що рівноважна траекторія росту зайнятості описується
рівнянням:
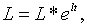
| (1.28) |
де
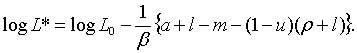 Тут неявно припускається, що
Тут неявно припускається, що 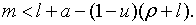 В протилежному випадку модель не має змісту, так як кількість використовуємої
робочої сили не може перевищувати її пропозиції.
З (1.18) випливає, рівноважний темп росту ставки заробітної плати рівний
В протилежному випадку модель не має змісту, так як кількість використовуємої
робочої сили не може перевищувати її пропозиції.
З (1.18) випливає, рівноважний темп росту ставки заробітної плати рівний 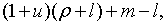 а з (1.5), (1.18), (1.20), та (1.28) випливає що рівноважний темп росту рівня
цін рівний темпу росту пропозиції грошей за винятком суми темпа росту
ефективності праці, росту пропозиції праці, обумовлених науково-технічним
прогресом. Параметр
а з (1.5), (1.18), (1.20), та (1.28) випливає що рівноважний темп росту рівня
цін рівний темпу росту пропозиції грошей за винятком суми темпа росту
ефективності праці, росту пропозиції праці, обумовлених науково-технічним
прогресом. Параметр 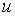 має назву еластичності попиту на гроші від доходу. З умови
має назву еластичності попиту на гроші від доходу. З умови 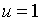 випливає, що при постійній норма відсотка задане збільшення доходу викликає
рівне пропорціональне збільшення попиту на гроші.
З рівнянь (1.12), (1.25) та (1.26) випливає, що у випадку, коли
випливає, що при постійній норма відсотка задане збільшення доходу викликає
рівне пропорціональне збільшення попиту на гроші.
З рівнянь (1.12), (1.25) та (1.26) випливає, що у випадку, коли 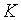 та
та 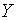 знаходятся на
своїх рівноважних траекторіях росту, норма відсотка рівна константі знаходятся на
своїх рівноважних траекторіях росту, норма відсотка рівна константі 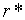 , яка визначається виразом:
, яка визначається виразом:
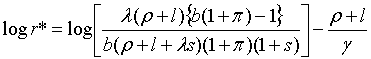
| (1.29) |
Відмітимо, що 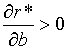 та та 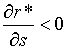 . Зміст одержаних результатів зводиться до того, що чим вище рівноважна норма
відсотка, тим більше значення грає капітал в процессі виробництва і тим нижце
схильність до заощадження. Другою цікавою властивістю виразу (1.29) є
незалежність
. Зміст одержаних результатів зводиться до того, що чим вище рівноважна норма
відсотка, тим більше значення грає капітал в процессі виробництва і тим нижце
схильність до заощадження. Другою цікавою властивістю виразу (1.29) є
незалежність 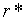 від
пропозиції грошей та параметрів переваги ліквідності — від
пропозиції грошей та параметрів переваги ліквідності — 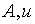 та
та 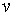 . Цей результат
пояснюється тим, що при умові коли всі змінні розташовані на своїх рівноважних
траекторіях росту ставка заробітної плати коректується по пропозиції грошей та
параметрам переваги ліквідності таким чином, що нейтралізувати їх вплив на
норму відсотка та реальні змінні системи.
Рівняння (1.13) та (1.29) дозволяють вияснити взаємовідношення між класичною
та кейнсіанською теорією відсотка. У відповідності з класичною теорією норма
відсотка визначається реальними факторами, впливаючими на заощадження та
попит на капітал, а по теорії Кейнса вирішальний вплив на норму відсотка
справляють явища грошового обороту. В розглядуємій моделі точка зору Кейнса,
яка виражається рівнянням (1.13), застосовна до фактичної норми відсотка в
довільний момент часу, а класична теорія, представлена рівнянням (1.29),
застосовна тількі до рівноважної норми відсотка.
З рівнянь (1.15) — (1.17) та (1.24) — (1.26) отримаємо:
де . Цей результат
пояснюється тим, що при умові коли всі змінні розташовані на своїх рівноважних
траекторіях росту ставка заробітної плати коректується по пропозиції грошей та
параметрам переваги ліквідності таким чином, що нейтралізувати їх вплив на
норму відсотка та реальні змінні системи.
Рівняння (1.13) та (1.29) дозволяють вияснити взаємовідношення між класичною
та кейнсіанською теорією відсотка. У відповідності з класичною теорією норма
відсотка визначається реальними факторами, впливаючими на заощадження та
попит на капітал, а по теорії Кейнса вирішальний вплив на норму відсотка
справляють явища грошового обороту. В розглядуємій моделі точка зору Кейнса,
яка виражається рівнянням (1.13), застосовна до фактичної норми відсотка в
довільний момент часу, а класична теорія, представлена рівнянням (1.29),
застосовна тількі до рівноважної норми відсотка.
З рівнянь (1.15) — (1.17) та (1.24) — (1.26) отримаємо:
де
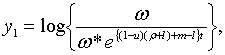
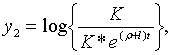
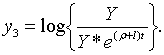 З (1.31) та (1.32) маємо:
З (1.31) та (1.32) маємо:
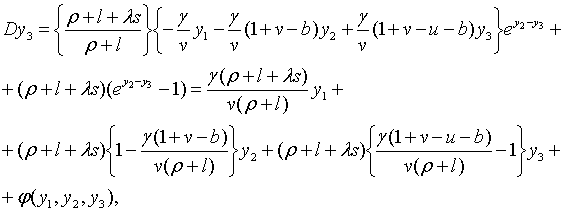
| (1.33) |
де відношення 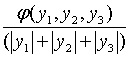 прямує до нуля, при прямує до нуля, при 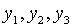 прямуючих до нуля.
Точні траекторії прямуючих до нуля.
Точні траекторії 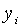 визначаються початковими значенням цих величін та рівняннями (1.30) — (1.32), а
наближені — початковими значеннями та системою лінійних рівнянь:
визначаються початковими значенням цих величін та рівняннями (1.30) — (1.32), а
наближені — початковими значеннями та системою лінійних рівнянь:
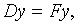
| (1.34) |
яка отримується якщо не враховувати 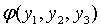 . Достатньою умовою того, щоб пропорційні відхілення
. Достатньою умовою того, щоб пропорційні відхілення 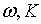 та
та 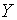 від їх
рівноважних траекторій росту прямували до нуля при від їх
рівноважних траекторій росту прямували до нуля при 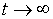 , є достатньо мала величіна відповідних початкових відхілень і наявність у
характеристичних корней функції
, є достатньо мала величіна відповідних початкових відхілень і наявність у
характеристичних корней функції 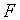 від’ємних дійсних частин.
Характеристичними корнями функції
від’ємних дійсних частин.
Характеристичними корнями функції 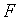 є корені рівняння: є корені рівняння:
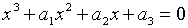
| (1.35) |
де
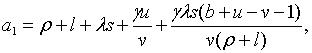
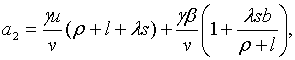
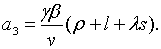 Необхідні та достатні умови того, щоб ці корені мали від’ємні дійсні частини,
виражаються нерівностями
Необхідні та достатні умови того, щоб ці корені мали від’ємні дійсні частини,
виражаються нерівностями 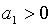 ,
, 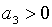 , , 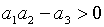 . Ці умови виконуються, якщо
. Ці умови виконуються, якщо 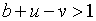 , але можуть порушуватись, якщо остання умова не має місця. Таким чином, при
значному впливі доходу на рівень попиту на гроші, тобто при великому значенні
, але можуть порушуватись, якщо остання умова не має місця. Таким чином, при
значному впливі доходу на рівень попиту на гроші, тобто при великому значенні 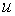 , відбувається стабілізація, а при сильному впливі норми відсотка на рівень
попиту на гроші, тобто при великому значенні
, відбувається стабілізація, а при сильному впливі норми відсотка на рівень
попиту на гроші, тобто при великому значенні 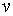 , виникає “вибухоподібний” рух системи.
Для того, щоб краще зрозуміти властивості моделі, розглянемо неформалізований
опис впливу збуджень на встановившийся стан системи. Припустимо, що всі
змінні знаходяться на своїх рівноважних траекторіях росту і що деяке збудження
викликає збільшення геометричного темпу росту реального споживання. Це призведе
до збільшення геометричного темпу росту випуску продукції, занятості та рівня
цін. Збільшення геометричних темпів реального доходу та рівня цін створить
тенденцію до збільшення геометричного темпу росту попиту на гроші. Відповідно,
при умові, коли геометричний темп росту пропозиції грошей не змінюється, буде
відбуватися ріст норми відсотка. Цей ріст викликає тенденцію до зменшення
геометричного темпу росту попиту на капітальні блага, в результаті чого
зупиниться відхилення вверх випуска продукції від його рівноважної траекторії
росту. Таким чином, при сильному впливі доходу на попит на гроші можна
очікувати, що цей вплив буде здійснювати стабілізуючий вплив на систему. Однак,
збільшення норми відсотка, обумовлене збільшенням геометричного темпу росту
реального доходу і цін, тим менше, чим більш відчутний вплив норма відсотка на
попит на гроші, бо в силу (1.8) зменшення попиту на гроші, викликане зростанням
норми відсотка, має бути достатнім для компенсації збільшення попиту на гроші,
викликаного відхіленням вверх фактичного доходу та рівня цін від їх рівноважних
траекторій росту. Відповідно, при суттевому впливі норми відсотка на попит на
гроші слід очікувати, що цей вплив дестабілізуюче діє на стан системи.
Д. Кейнс висунув думку, що еластичність попиту на гроші від норми відсотка
, виникає “вибухоподібний” рух системи.
Для того, щоб краще зрозуміти властивості моделі, розглянемо неформалізований
опис впливу збуджень на встановившийся стан системи. Припустимо, що всі
змінні знаходяться на своїх рівноважних траекторіях росту і що деяке збудження
викликає збільшення геометричного темпу росту реального споживання. Це призведе
до збільшення геометричного темпу росту випуску продукції, занятості та рівня
цін. Збільшення геометричних темпів реального доходу та рівня цін створить
тенденцію до збільшення геометричного темпу росту попиту на гроші. Відповідно,
при умові, коли геометричний темп росту пропозиції грошей не змінюється, буде
відбуватися ріст норми відсотка. Цей ріст викликає тенденцію до зменшення
геометричного темпу росту попиту на капітальні блага, в результаті чого
зупиниться відхилення вверх випуска продукції від його рівноважної траекторії
росту. Таким чином, при сильному впливі доходу на попит на гроші можна
очікувати, що цей вплив буде здійснювати стабілізуючий вплив на систему. Однак,
збільшення норми відсотка, обумовлене збільшенням геометричного темпу росту
реального доходу і цін, тим менше, чим більш відчутний вплив норма відсотка на
попит на гроші, бо в силу (1.8) зменшення попиту на гроші, викликане зростанням
норми відсотка, має бути достатнім для компенсації збільшення попиту на гроші,
викликаного відхіленням вверх фактичного доходу та рівня цін від їх рівноважних
траекторій росту. Відповідно, при суттевому впливі норми відсотка на попит на
гроші слід очікувати, що цей вплив дестабілізуюче діє на стан системи.
Д. Кейнс висунув думку, що еластичність попиту на гроші від норми відсотка 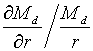 може бути зростаючою функцією
може бути зростаючою функцією 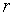 і прямує до
і прямує до 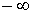 по мірі
того, як по мірі
того, як 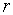 від своєї
верхньої межи наближається до деякого додатнього числа. З рівняння (1.7)
випливає, що еластичність попиту на гроші від норми відсотка є константа, рівна від своєї
верхньої межи наближається до деякого додатнього числа. З рівняння (1.7)
випливає, що еластичність попиту на гроші від норми відсотка є константа, рівна 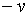 . Якщо б гіпотеза Кейнса була вірна, розглядуєма модель страждалаб одним
принциповим недоліком. Однак, отримані до сих пір емпіричні дані не
підтверджують вказаної гіпотези. Так, виконаний Бронфербергом та Майером аналіз
даних по США за період 1919 – 1956 рр. не дає приводу відкидувати припущення,
що еластичність попиту на гроші від норми відсотка є константа.
Приймемо, наприклад, слідуючі значення параметрів:
. Якщо б гіпотеза Кейнса була вірна, розглядуєма модель страждалаб одним
принциповим недоліком. Однак, отримані до сих пір емпіричні дані не
підтверджують вказаної гіпотези. Так, виконаний Бронфербергом та Майером аналіз
даних по США за період 1919 – 1956 рр. не дає приводу відкидувати припущення,
що еластичність попиту на гроші від норми відсотка є константа.
Приймемо, наприклад, слідуючі значення параметрів: 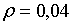 ;
; 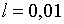 ; ; 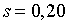 ;
; 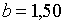 ; ; 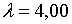 ;
; 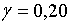 ; ; 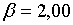 . Параметр
. Параметр 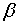 приблизно рівний відсотковому збільшення темпу росту ставки заробітної плати,
відповідаючому, підвищенню рівня зайнятості на 1%. Прийняте значення цього
параметру базується на даних по Англії. Параметр s рівний частці
приросту реального доходу, напрамляємого на заощадження, і має назву
граничної схильності до заощадження. Величини
приблизно рівний відсотковому збільшення темпу росту ставки заробітної плати,
відповідаючому, підвищенню рівня зайнятості на 1%. Прийняте значення цього
параметру базується на даних по Англії. Параметр s рівний частці
приросту реального доходу, напрамляємого на заощадження, і має назву
граничної схильності до заощадження. Величини 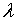 та
та 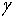 називаються
швидкодією, а обернені їм величини — середнім значенням часового
запізнення. Параметр називаються
швидкодією, а обернені їм величини — середнім значенням часового
запізнення. Параметр 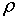 – додатня константа фігуруюча у виробничій функції Кобба-Дугласа
– додатня константа фігуруюча у виробничій функції Кобба-Дугласа 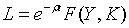 яка пов’язує чисельність використовуємої робочої сили з реальним випуском
продукції та об’ємом використовуємого капіталу.
При вказаних значеннях всіх параметрів, окрім
яка пов’язує чисельність використовуємої робочої сили з реальним випуском
продукції та об’ємом використовуємого капіталу.
При вказаних значеннях всіх параметрів, окрім 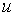 та
та 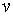 , умова стійкості
системи записується нерівністю: , умова стійкості
системи записується нерівністю:
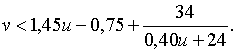
| (1.36) |
Якщо, як це часто приймається, 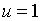 , то ця умова виконується при
, то ця умова виконується при 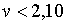 , а якщо
, а якщо 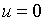 , то умова
стійкості виконується при , то умова
стійкості виконується при 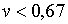 . Різні емпіричні оцінки еластичності попиту на гроші від норми відсотка по
даним, які відносяться до Англії та США, лежать в межах від 0 до
–2,0. При близьких до дійсних значеннях
. Різні емпіричні оцінки еластичності попиту на гроші від норми відсотка по
даним, які відносяться до Англії та США, лежать в межах від 0 до
–2,0. При близьких до дійсних значеннях 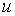 та
та 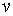 , задовільняючих
нерівності (1.36), два з трьох коренів рівняння (1.35) комплексні, так що
модель породжує затухаючий цикл біля тенденції до рівноважної траекторії росту. , задовільняючих
нерівності (1.36), два з трьох коренів рівняння (1.35) комплексні, так що
модель породжує затухаючий цикл біля тенденції до рівноважної траекторії росту.
Економічне регулювання
Мета цього розділу полягає у тому, щоб дослідити як змінюється поведінка
моделі циклічного росту при введенні різноманітних зворотніх зв’язків,
відображаючих той інший курс грошової та фіскальної політики. Таке
дослідження можна розглядати як задачу прогнозування в широкому аспекті.
Разом с тим воно наочно демонструє одну з найбільш важливих можливостей
використання макроекономічних моделей. Крім того, навіть з точки зору чистого
прогнозування важливо, щоб співвідношення які описує вплив зворотніх зв’язків
були включені в модедь, особливо ті з них, які відображають курси політики,
що проводиться державними органами.
Грошова політика
У попередньому розділі грошова політика була нейтральною в тому розумінні, що
пропозиція грошей була зростаючою в геометричній прогрессії. Припустимо
тепер, що пропозиція гроней неперервно змінюється відповідно до змін інших
змінних моделі.
Розглянемо спочатку політику, що описується рівнянням
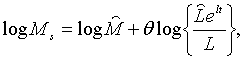
| (2.1.1) |
де 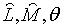 — додатні константи.
Припустимо, що — додатні константи.
Припустимо, що 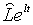 задає траекторію зайнятості, яка вважається оптимальною. Оскількі пропозиція
робочої сили відповідає траекторії
задає траекторію зайнятості, яка вважається оптимальною. Оскількі пропозиція
робочої сили відповідає траекторії 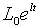 оптимальний пропорційний рівень зайнятості визначається відношенням
оптимальний пропорційний рівень зайнятості визначається відношенням 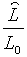 . Це відношення, яке не перевищує одиницю відображає оптимальний баланс між
безробіттям та інфляцією. Рівняння (2.1.1) базується на припущенні, що при
оптимальному рівні зайнятості пропозиція грошей постійна і рівна
. Це відношення, яке не перевищує одиницю відображає оптимальний баланс між
безробіттям та інфляцією. Рівняння (2.1.1) базується на припущенні, що при
оптимальному рівні зайнятості пропозиція грошей постійна і рівна 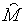 , в противному випадку пропорційне перевищення
, в противному випадку пропорційне перевищення 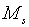 над
над 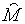 є зростаючою
функцією пропорційного перевищення є зростаючою
функцією пропорційного перевищення 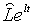 над
над 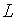 . Тепер замість
рівняння (1.10) використовується рівняння (2.1.1), так, що модель включає
рівняння (1.1) — (1.9) і (2.1.1).
З (1.7), (1.8) і (2.1.1) отримаємо . Тепер замість
рівняння (1.10) використовується рівняння (2.1.1), так, що модель включає
рівняння (1.1) — (1.9) і (2.1.1).
З (1.7), (1.8) і (2.1.1) отримаємо
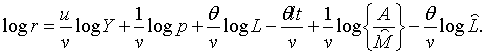
| (2.1.2) |
Тоді з (1.12) та (2.1.2) отримаємо
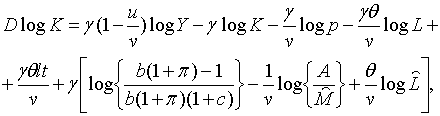
| (2.1.3) |
що разом з (1.4) та (1.5) дає
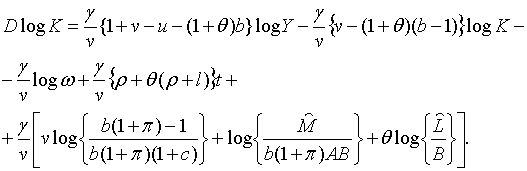
| (2.1.4) |
Одночасно також маємо
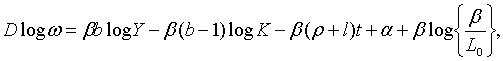
| (2.1.5) | 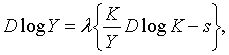
| (2.1.6) |
що аналогічно відповідно (1.16) та (1.17).
Траекторія зміни змінних 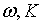 та
та 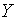 визначається
початковими значеннями змінних і системою рівнянь (2.1.4) — (2.1.6). Частинний
розв’язок цієї системи має вигляд
де
Із (1.4), (2.1.8), (2.1.9) та (2.1.12) випливає,що рівноважна траекторія
росту зайнятості визначається рівнянням визначається
початковими значеннями змінних і системою рівнянь (2.1.4) — (2.1.6). Частинний
розв’язок цієї системи має вигляд
де
Із (1.4), (2.1.8), (2.1.9) та (2.1.12) випливає,що рівноважна траекторія
росту зайнятості визначається рівнянням
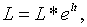
| (2.1.13) |
де
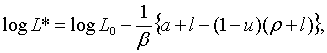 Таким чином, ця траекторія не пов’язана з оптимальною. Дійсно, порівняння
(1.28) з (2.1.13) показує, що рівноважна траекторія росту зайнятості
співпадає з траекторією, що відповідає постійній пропозиції грошей. Це
неприйнятний наслідок політики, що описується рівнянням (2.1.1). Розглянемо
тепер вплив цієї політики на стійкість системи.
З рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13) маємо
Таким чином, ця траекторія не пов’язана з оптимальною. Дійсно, порівняння
(1.28) з (2.1.13) показує, що рівноважна траекторія росту зайнятості
співпадає з траекторією, що відповідає постійній пропозиції грошей. Це
неприйнятний наслідок політики, що описується рівнянням (2.1.1). Розглянемо
тепер вплив цієї політики на стійкість системи.
З рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13) маємо
Страницы: 1, 2
|
|
|
|
|

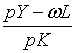 , таким чином, можна рахувати нормою прибутку на основний капітал.
Це рівняння виводиться з припущення, що пропорційний темп росту інвестицій в
основний капітал є зростаюча функція відношення норми прибутку на основний
капітал до норми відсотка. Параметр
, таким чином, можна рахувати нормою прибутку на основний капітал.
Це рівняння виводиться з припущення, що пропорційний темп росту інвестицій в
основний капітал є зростаюча функція відношення норми прибутку на основний
капітал до норми відсотка. Параметр 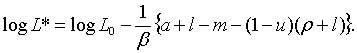 Тут неявно припускається, що
Тут неявно припускається, що 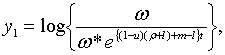
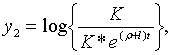
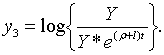 З (1.31) та (1.32) маємо:
З (1.31) та (1.32) маємо:
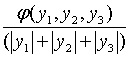 прямує до нуля, при
прямує до нуля, при 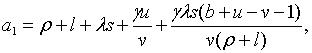
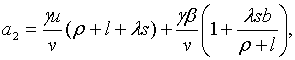
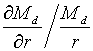 може бути зростаючою функцією
може бути зростаючою функцією 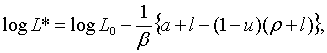 Таким чином, ця траекторія не пов’язана з оптимальною. Дійсно, порівняння
(1.28) з (2.1.13) показує, що рівноважна траекторія росту зайнятості
співпадає з траекторією, що відповідає постійній пропозиції грошей. Це
неприйнятний наслідок політики, що описується рівнянням (2.1.1). Розглянемо
тепер вплив цієї політики на стійкість системи.
З рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13) маємо
Таким чином, ця траекторія не пов’язана з оптимальною. Дійсно, порівняння
(1.28) з (2.1.13) показує, що рівноважна траекторія росту зайнятості
співпадає з траекторією, що відповідає постійній пропозиції грошей. Це
неприйнятний наслідок політики, що описується рівнянням (2.1.1). Розглянемо
тепер вплив цієї політики на стійкість системи.
З рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13) маємо