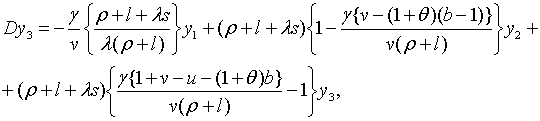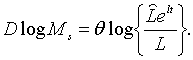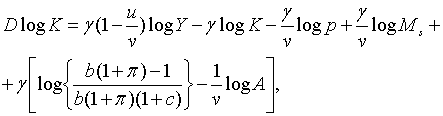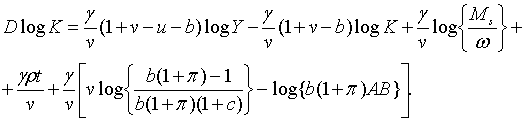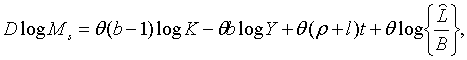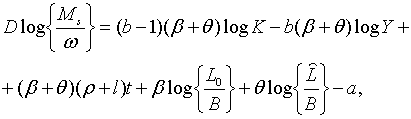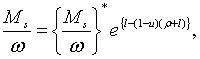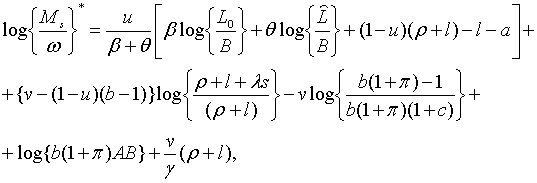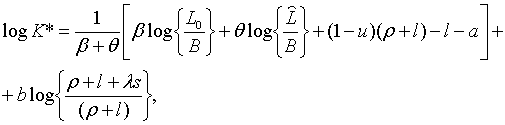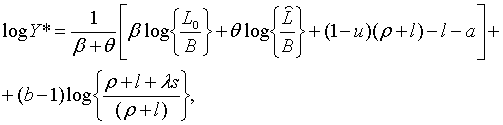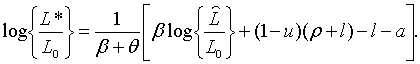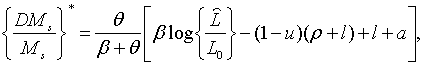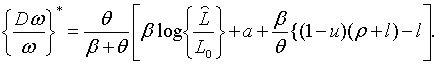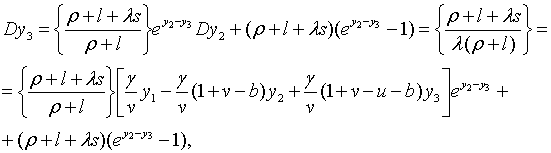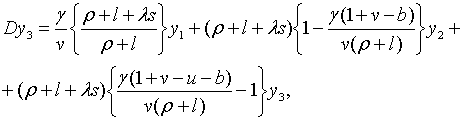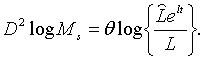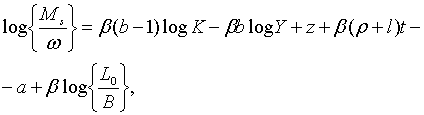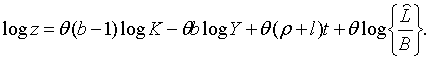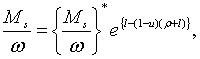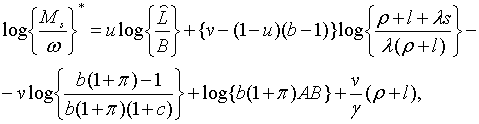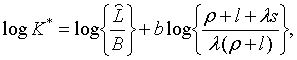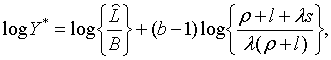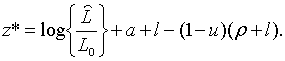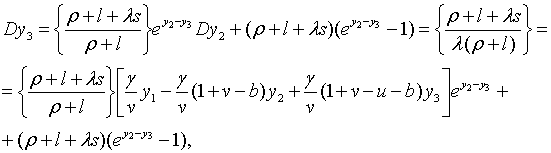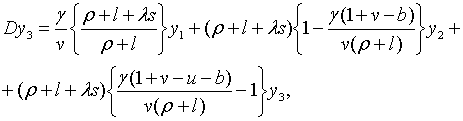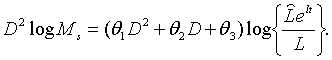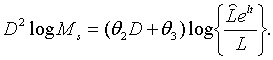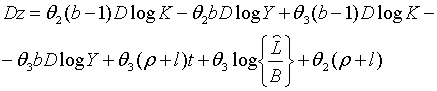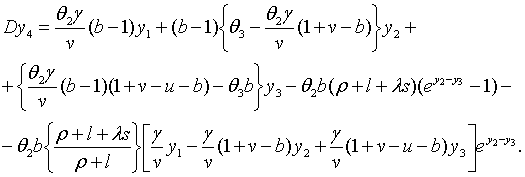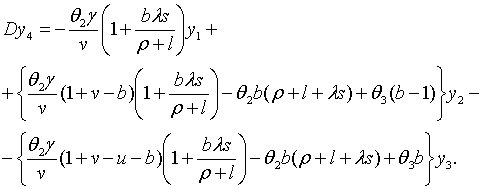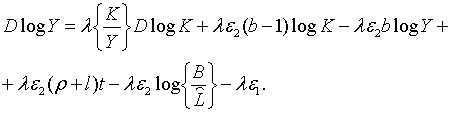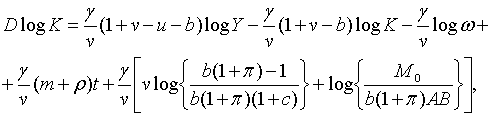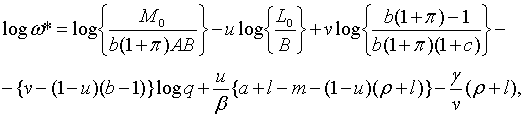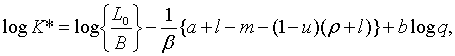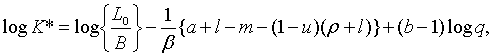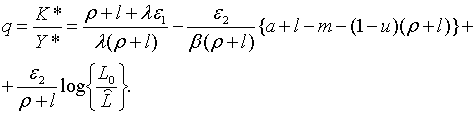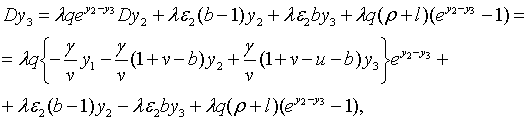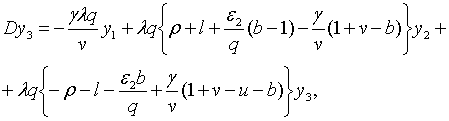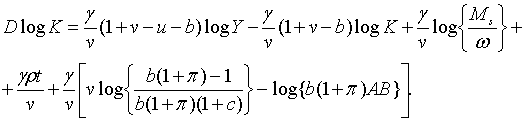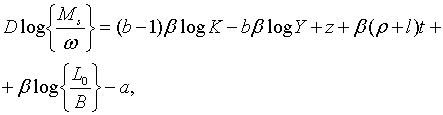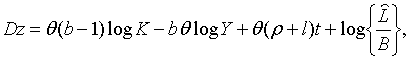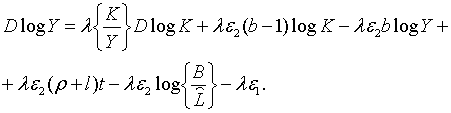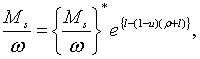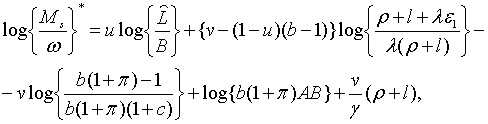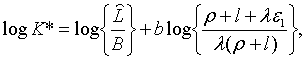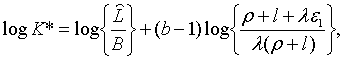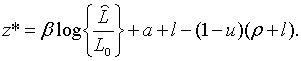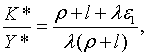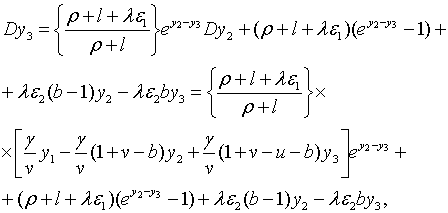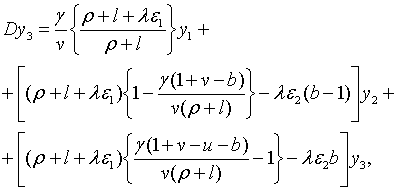|
|
|
|
Курсовая: Математические модели инфляции
де
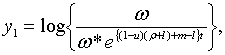
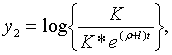
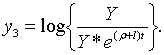 Точні траекторії зміни змінних
Точні траекторії зміни змінних 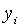 визначаються початковими значеннями цих змінних і системою рівнянь (2.1.4) —
(2.1.6) та (2.1.10) — (2.1.13), а наближені траекторії – тими ж початковими
значеннями і системою лінійних рівнянь, які включають (2.1.14), (2.1.15) та
визначаються початковими значеннями цих змінних і системою рівнянь (2.1.4) —
(2.1.6) та (2.1.10) — (2.1.13), а наближені траекторії – тими ж початковими
значеннями і системою лінійних рівнянь, які включають (2.1.14), (2.1.15) та
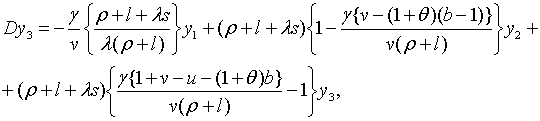
| (2.1.17) |
Характеристичними коренями матриці коефіцієнтів останньої системи є корені
рівняння
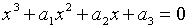 , ,
| (2.1.18) |
де
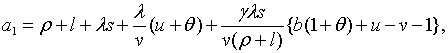
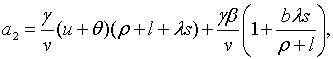
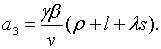 Зауважимо, що
Зауважимо, що 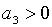 , , 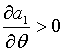 , і при умові, що
, і при умові, що 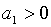 частинна похідна
частинна похідна 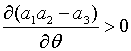 .
Отже, хоч політика задана рівнянням (2.1.1) не впливає на рівноважну траекторію
зайнятості (на відміну від політики, що передбачає постійну пропозицію грошей),
вона може справляти стабілізуючу дію.
Припустимо, наприклад, що .
Отже, хоч політика задана рівнянням (2.1.1) не впливає на рівноважну траекторію
зайнятості (на відміну від політики, що передбачає постійну пропозицію грошей),
вона може справляти стабілізуючу дію.
Припустимо, наприклад, що 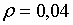 ;
; 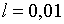 ; ; 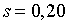 ;
; 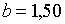 ; ; 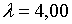 ;
; 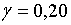 ; ; 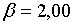 ;
; 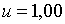 ; ; 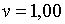 .При цих умовах і при
.При цих умовах і при 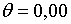 корені рівняння (2.1.18) рівні
корені рівняння (2.1.18) рівні 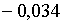 ;
; 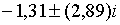 , а при , а при 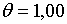 ці корені рівні
ці корені рівні 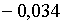 ; ; 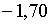 ;
; 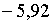 . Тобто у даному
випадку вплив грошової політики приводить до поступової ліквідації ціклу і
більш швидкої збіжності до довгострокового тренду.
Розглянемо тепер політику, яка визначається рівнянням . Тобто у даному
випадку вплив грошової політики приводить до поступової ліквідації ціклу і
більш швидкої збіжності до довгострокового тренду.
Розглянемо тепер політику, яка визначається рівнянням
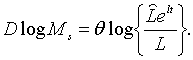
| (2.1.19) |
З цього рівняння випливає, що при оптимальному рівні зайнятості пропозиція
грошей постійна. В протилежному випадку пропорційний темп росту пропозиції
грошей, є зростаючою функцією пропорціонального перевищення 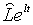 над
над 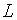 . Тепер модель
описується рівняннями (1.1), (1.9) та (2.1.19).
З (1.7), (1.8) та (1.12) маємо . Тепер модель
описується рівняннями (1.1), (1.9) та (2.1.19).
З (1.7), (1.8) та (1.12) маємо
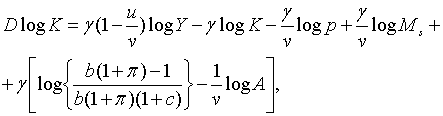
| (2.1.20) |
що у сукупності з (1.4) та (1.5) дає
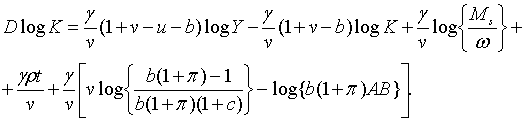
| (2.1.21) |
Далі, з (1.4) та (1.19) маємо
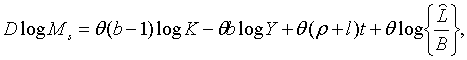
| (2.1.22) |
що разом з (2.1.5) дає
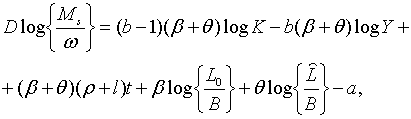
| (2.1.23) |
Траекторії зміни 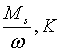 та та 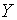 визначаються початковими значеннями змінних та системою рівнянь, що включає
(2.1.6), (2.1.21) та (2.1.23). (Власні траекторії
визначаються початковими значеннями змінних та системою рівнянь, що включає
(2.1.6), (2.1.21) та (2.1.23). (Власні траекторії 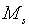 та
та 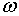 можна отримати,
використовуючи (2.1.5) та (2.1.22).) Частинний розв’язок системи має вигляд
де можна отримати,
використовуючи (2.1.5) та (2.1.22).) Частинний розв’язок системи має вигляд
де
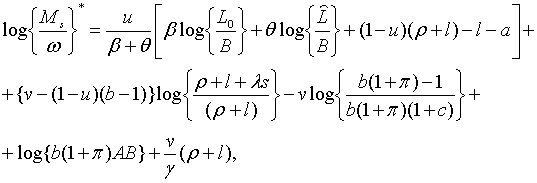
| (2.1.27) | 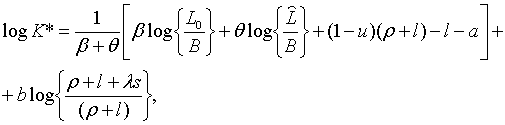
| (2.1.28) | 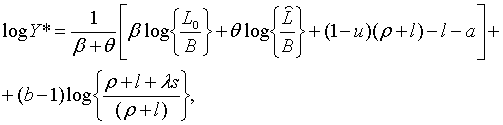
| (2.1.29) |
P (1.4), (2.1.25), (2.1.26), (2.1.28) та (2.1.29) випливає, що рівноважна
траекторі росту зайнятості визначається рівнянням
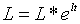 , ,
| (2.1.30) |
де
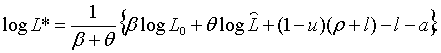 Крім того маємо
Крім того маємо
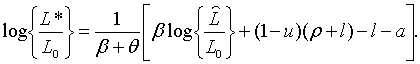
| (2.1.31) |
Зміст (2.1.31) полягає в тому, що рівноважний пропорційний рівень зайнятості 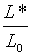 , при політиці, заданій рівнянням (2.1.19) є зваженим середнім геометричним
оптимального пропорційного рівня зайнятості
, при політиці, заданій рівнянням (2.1.19) є зваженим середнім геометричним
оптимального пропорційного рівня зайнятості 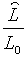 та рівноважного пропорційного рівня зайнятості при умові постійної пропозиції
грошей. [див. (1.28) та (2.1.13)]. Різниця між
та рівноважного пропорційного рівня зайнятості при умові постійної пропозиції
грошей. [див. (1.28) та (2.1.13)]. Різниця між 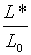 та
та 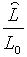 тим менша, чим
більше тим менша, чим
більше 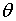 і прямує до
нуля коли і прямує до
нуля коли 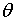 прямує
до нескінченості. таким Чином політика (2.1.19) веде до зменшення, але не
усуває повністю відмінності між рівноважним і оптимальним пропорційними рівнями
зайнатості. В цьому відношенні вона більш ефективна, ніж політика (2.1.1), хоча
і її не можна вважати цілко задовільною.
Слід зауважити, що при політиці (2.1.12) пропозиція грошей продовжує
змінюватись, поки рівень зайнятості не досягає оптимуму. Тому, досить
несподівано, що ця політика, не забазпечує рівності прямує
до нескінченості. таким Чином політика (2.1.19) веде до зменшення, але не
усуває повністю відмінності між рівноважним і оптимальним пропорційними рівнями
зайнатості. В цьому відношенні вона більш ефективна, ніж політика (2.1.1), хоча
і її не можна вважати цілко задовільною.
Слід зауважити, що при політиці (2.1.12) пропозиція грошей продовжує
змінюватись, поки рівень зайнятості не досягає оптимуму. Тому, досить
несподівано, що ця політика, не забазпечує рівності 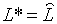 . Це пояснюється тим, що у встановленому стані системи ставка заробітної плати
змінюється зі швидкістю, яка цілком компенсує вплив на пропорційний рівень
зайнятості зміни пропозиції грошей. Пропорційні темпи росту ставки заробітної
плати та пропозиції грошей в усталеному стані системи легко отримати з рівняння
(2.1.5), (2.1.19), (2.1.25) та (2.1.30). Вони визначаються виразами
. Це пояснюється тим, що у встановленому стані системи ставка заробітної плати
змінюється зі швидкістю, яка цілком компенсує вплив на пропорційний рівень
зайнятості зміни пропозиції грошей. Пропорційні темпи росту ставки заробітної
плати та пропозиції грошей в усталеному стані системи легко отримати з рівняння
(2.1.5), (2.1.19), (2.1.25) та (2.1.30). Вони визначаються виразами
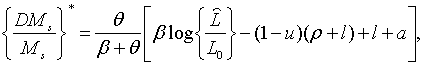
| (2.1.32) | 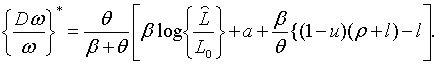
| (2.1.33) |
З (2.1.6), (2.1.21), (2.1.23) та (2.1.27) — (2.1.29) маємо
де
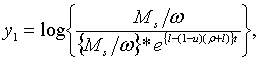
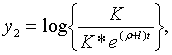
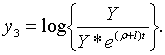 Точні траекторії
Точні траекторії 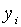 визначаються початковими значенням цих величін та рівняннями (2.1.32) —
(2.1.33), а наближені — тими ж початковими значеннями та системою лінійних
рівнянь (2.1.34), (2.1.35) та
визначаються початковими значенням цих величін та рівняннями (2.1.32) —
(2.1.33), а наближені — тими ж початковими значеннями та системою лінійних
рівнянь (2.1.34), (2.1.35) та
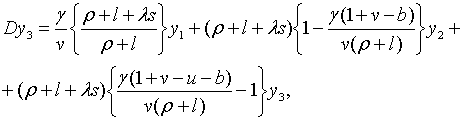
| (2.1.37) |
Характеристичними коренями матриці коефіцієнтів останньої системи є корені
рівняння
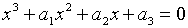 , ,
| (2.1.18) |
де
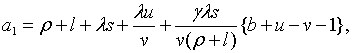
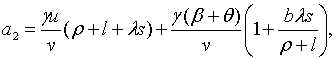
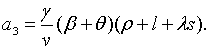 Зауважимо, що
Зауважимо, що 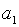 не
залежить від не
залежить від 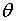 і що
навіть при умові, коли і що
навіть при умові, коли 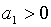 , похідна
, похідна 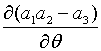 може
бути від’ємною. Цей результат демонструє, що політика (2.1.19) менш ефективна з
точки зору стабілізації системи, ніж політика (2.1.1).
Припустимо, наприклад, що може
бути від’ємною. Цей результат демонструє, що політика (2.1.19) менш ефективна з
точки зору стабілізації системи, ніж політика (2.1.1).
Припустимо, наприклад, що 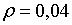 ;
; 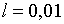 ; ; 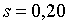 ;
; 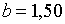 ; ; 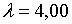 ;
; 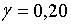 ; ; 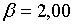 ;
; 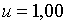 ; ; 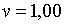 .При цих умовах і при
.При цих умовах і при 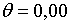 корені рівняння (2.1.18) рівні
корені рівняння (2.1.18) рівні 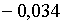 ;
; 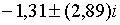 , а при , а при 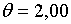 ці корені рівні
ці корені рівні 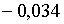 ; ; 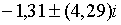 . Тобто у даному випадку грошова політика не справляє особливого демпфуючого
впливу на циклічний характер розвитку економіки. Її основний ефект полягає в
зменшенні різниці між рівноважним та оптимальним пропорційними рівнями
зайнятості та в зменшенні тривалості періода циклу.
Розглянемо тепер політику, яка визначається рівнянням
. Тобто у даному випадку грошова політика не справляє особливого демпфуючого
впливу на циклічний характер розвитку економіки. Її основний ефект полягає в
зменшенні різниці між рівноважним та оптимальним пропорційними рівнями
зайнятості та в зменшенні тривалості періода циклу.
Розглянемо тепер політику, яка визначається рівнянням
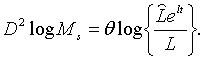
| (2.1.19) |
З цього рівняння випливає, що пропорційний темп росту пропозиції грошей
зменшується, залишається постійним або зростає, в залежності від того,
більший, рівний або менший оптимального фактичний рівень зайнятості. Вцьому
випадку модельописується рівняннями (1.1) — (1.9) та (2.1.39).
Введемо нову змінну 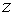 , яка визначається співвідношенням , яка визначається співвідношенням
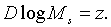
| (2.1.40) |
Тоді з (2.1.5) та (2.1.40) маємо
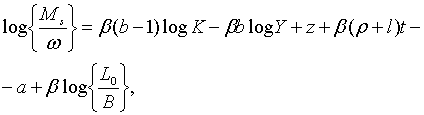
| (2.1.41) |
З (1.4), (2.1.29) та (2.1.40) отримаємо
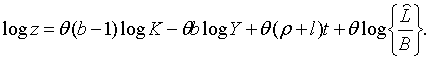
| (2.1.42) |
Траекторії зміни змінних 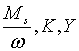 та
та 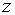 визначаються
початковими значеннями цих змінних та системою рівнянь, що включає (2.1.6),
(2.1.21), (2.1.41) та (2.1.42). Ця система має частинний розв’язок: визначаються
початковими значеннями цих змінних та системою рівнянь, що включає (2.1.6),
(2.1.21), (2.1.41) та (2.1.42). Ця система має частинний розв’язок:
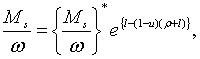
| (2.1.43) | 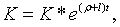
| (2.1.44) | 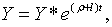
| (2.1.45) | 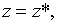
| (2.1.46) |
де
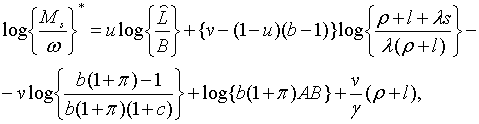
| (2.1.47) | 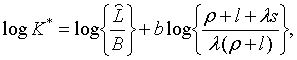
| (2.1.48) | 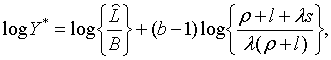
| (2.1.49) | 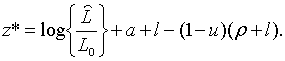
| (2.1.50) |
З (1.4), (2.1.44), (2.1.45), (2.1.48) та (2.1.49) випливає, що рівноважна
траекторія росту зайнятості визначається рівнянням
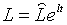 . .
| (6.1.51) |
Таким чином, рівноважна та оптимальна траекторія зайнятості співпадають. В
цьому відношенні політика (2.1.39) ефективніша, за політики (2.1.1) та
(2.1.19).
З (2.1.6) , (2.1.21), (2.1.41), (2.1.42) та (2.1.47) — (2.1.50) маємо
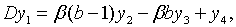
| (2.1.52) | 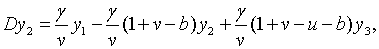
| (2.1.53) | 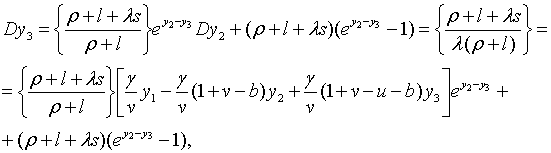
| (2.1.54) | 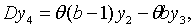
| (2.1.55) |
де
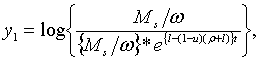
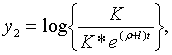
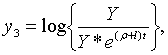
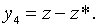 Точні траекторії зміни змінних
Точні траекторії зміни змінних 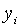 визначаються початковими значеннями цих змінних і системою рівнянь (2.1.52) —
(2.1.55), а наближені траекторії – тими ж початковими значеннями і системою
лінійних рівнянь, які включають (2.1.52), (2.1.53), (2.1.55) та
визначаються початковими значеннями цих змінних і системою рівнянь (2.1.52) —
(2.1.55), а наближені траекторії – тими ж початковими значеннями і системою
лінійних рівнянь, які включають (2.1.52), (2.1.53), (2.1.55) та
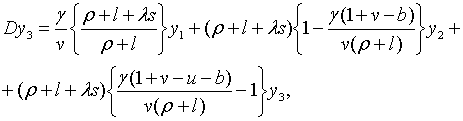
| (2.1.56) |
Характеристичними коренями матриці коефіцієнтів останньої системи є корені
рівняння
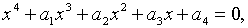
| (2.1.57) |
де
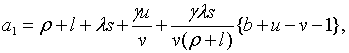
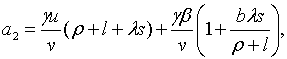
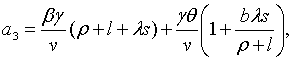
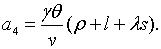 Необхідні і достатні умови від’ємності дійсних частин цих коренів задаються
нерівностями:
Необхідні і достатні умови від’ємності дійсних частин цих коренів задаються
нерівностями: 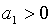 , , 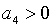 ,
, 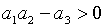 , , 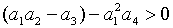 . Відмітимо, що
. Відмітимо, що 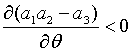 .
Відповідно, політика (2.1.39) може справляти дестабілізуючу дію.
Припустимо, наприклад, що .
Відповідно, політика (2.1.39) може справляти дестабілізуючу дію.
Припустимо, наприклад, що 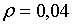 ;
; 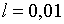 ; ; 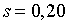 ;
; 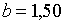 ; ; 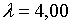 ;
; 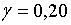 ; ; 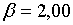 ;
; 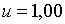 ; ; 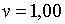 ,
, 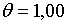 корені рівняння
(2.1.57) рівні корені рівняння
(2.1.57) рівні 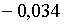 ; ; 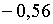 ;
; 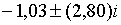 . Порівняння
цього результату, з результатом, отриманим при допушенні постійної пропозиції
грошей показує, що в цьому випадку один з проявів грошової політики зводиться
до зменшення демпфування циклу.
Політика (2.1.1), (2.1.19) та (2.1.39) є частинними випадками більш загальної
політики, що описується рівнянням . Порівняння
цього результату, з результатом, отриманим при допушенні постійної пропозиції
грошей показує, що в цьому випадку один з проявів грошової політики зводиться
до зменшення демпфування циклу.
Політика (2.1.1), (2.1.19) та (2.1.39) є частинними випадками більш загальної
політики, що описується рівнянням
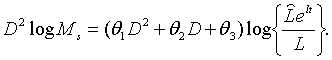
| (2.1.58) |
З рівняння (2.1.1) випливає що 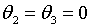 , із (2.1.19) – що
, із (2.1.19) – що 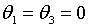 ,
а із (2.1.39) – що ,
а із (2.1.39) – що 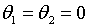 . У найбільш ефективної політики такого типу, зрозуміло, всі три параметри
повинні мати додатні значення. Розглянемо тепер дещо менш загальний випадок,
коли
. У найбільш ефективної політики такого типу, зрозуміло, всі три параметри
повинні мати додатні значення. Розглянемо тепер дещо менш загальний випадок,
коли 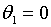 , , 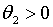 ,
, 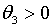 . В цьому випадку
рівняння (2.1.58) має вигляд . В цьому випадку
рівняння (2.1.58) має вигляд
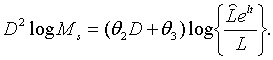
| (2.1.59) |
і повна модель описується рівнянням (1.1) — (1.9) та (2.1.59).
Із (1.4), (2.1.40) та (2.1.59) маємо
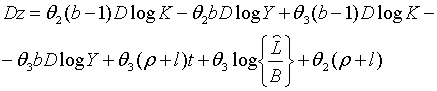
| (2.1.60) |
Траекторії зміни змінних 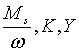 та
та 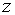 визначаються
початковими значеннями цих змінних та системою рівнянь, що включає (2.1.6),
(2.1.21), (2.1.41) та (2.1.60). Рівноважні траекторії росту цих змінних
задаються рівняннями (2.1.43) — (2.1.50), а рівноважна траекторія росту
зайнятості – рівнянням (2.1.51). Таким чином рівноважна та оптимальна
траекторії зайнятості співпадають. Цей результат отримується, по суті, при
довільній політиці, яку можна описати рівнянням виду (2.1.58) при умові визначаються
початковими значеннями цих змінних та системою рівнянь, що включає (2.1.6),
(2.1.21), (2.1.41) та (2.1.60). Рівноважні траекторії росту цих змінних
задаються рівняннями (2.1.43) — (2.1.50), а рівноважна траекторія росту
зайнятості – рівнянням (2.1.51). Таким чином рівноважна та оптимальна
траекторії зайнятості співпадають. Цей результат отримується, по суті, при
довільній політиці, яку можна описати рівнянням виду (2.1.58) при умові 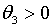 .
З (2.1.60) та (2.1.48) — (2.1.50) маємо
.
З (2.1.60) та (2.1.48) — (2.1.50) маємо
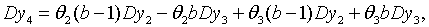
| (2.1.61) |
де змінні 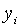 визначаються аналогічно з (2.1.55). Справедливі в даному випадку і
співвідношення (2.1.52) — (2.1.54). З (2.1.53), (2.1.54) та (2.1.61) отримаємо
визначаються аналогічно з (2.1.55). Справедливі в даному випадку і
співвідношення (2.1.52) — (2.1.54). З (2.1.53), (2.1.54) та (2.1.61) отримаємо
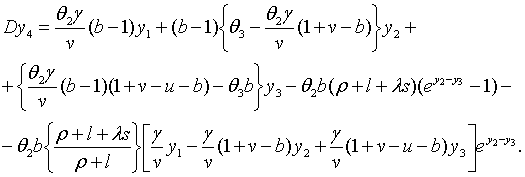
| (2.1.62) |
Точні траекторії зміни 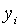 визначаються початковими значеннями цих змінних і системою рівнянь (2.1.52) —
(2.1.54) та (2.1.62), а наближені траекторії – тими ж початковими значеннями і
системою лінійних рівнянь, які включають (2.1.52), (2.1.53), (2.1.56) та
визначаються початковими значеннями цих змінних і системою рівнянь (2.1.52) —
(2.1.54) та (2.1.62), а наближені траекторії – тими ж початковими значеннями і
системою лінійних рівнянь, які включають (2.1.52), (2.1.53), (2.1.56) та
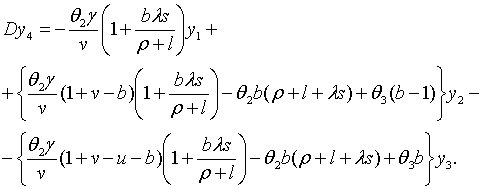
| (2.1.63) |
Припустимо, наприклад, що задані такі значення праметрів: 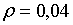 ;
; 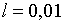 ; ; 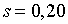 ;
; 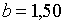 ; ; 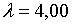 ;
; 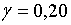 ; ; 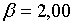 ;
; 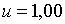 ; ; 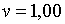 ;
; 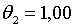 ; ; 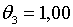 . При цих умовахнаближена система має вигляд
. При цих умовахнаближена система має вигляд
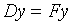
| (2.1.64) |
де
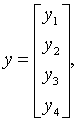 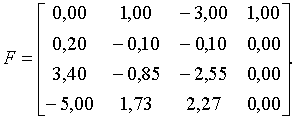 Характеристичні корені
Характеристичні корені 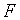 рівні:
рівні: 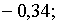 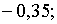 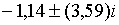 . Тобто, в порівнянні з випадком, коли
. Тобто, в порівнянні з випадком, коли 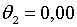 та
та 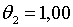 , демпфування
циклю збільшується, але період скорочується. , демпфування
циклю збільшується, але період скорочується.
Бюджетна політика
В розглядуємій моделі поки що, формально не враховувались державні витрати та
податки. Однак величіну 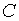 можна вважати сумою реального особистого споживання та реальних поточних
державних витрат на товари та послуги. А
можна вважати сумою реального особистого споживання та реальних поточних
державних витрат на товари та послуги. А 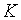 відповідає сумі державного та приватного основного капіталу. Тоді з рівняння
(1.1) випливає, що величина
відповідає сумі державного та приватного основного капіталу. Тоді з рівняння
(1.1) випливає, що величина 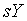 рівна сумі реальних приватних та державних заощаджень, де останні визначаються
як перевищення реальних надходжень від податків над реальними поточними
державними витратами на товари та послуги. При цьому параметр
рівна сумі реальних приватних та державних заощаджень, де останні визначаються
як перевищення реальних надходжень від податків над реальними поточними
державними витратами на товари та послуги. При цьому параметр 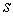 залежить від трьох відношень: 1. відношення особистого споживання до особистого
доходу; 2. відношення надходжень від податків до доходу (тобто середній нормі
оподаткування); 3. відношення поточних державних витрат на товари та послуги до
надходжень від податків. До цих пір в неявному вигляді припускалося, що ці три
відношення постійні. Нехай тепер друге і трете відношення змінюються відповідно
змінам пропорційного рівня зайнятості. Отже величина
залежить від трьох відношень: 1. відношення особистого споживання до особистого
доходу; 2. відношення надходжень від податків до доходу (тобто середній нормі
оподаткування); 3. відношення поточних державних витрат на товари та послуги до
надходжень від податків. До цих пір в неявному вигляді припускалося, що ці три
відношення постійні. Нехай тепер друге і трете відношення змінюються відповідно
змінам пропорційного рівня зайнятості. Отже величина 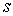 тепер буде розглядатися на як змінна, а як параметр.
Припустимо, зокрема, що
тепер буде розглядатися на як змінна, а як параметр.
Припустимо, зокрема, що
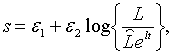
| (2.2.1) |
де 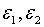 — додатні
константи. Тоді повна модель буде описуватися рівняннями (1.1) — (1.10) та
(2.2.1). Із (1.4) та (2.2.1) випливає — додатні
константи. Тоді повна модель буде описуватися рівняннями (1.1) — (1.10) та
(2.2.1). Із (1.4) та (2.2.1) випливає
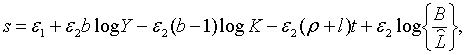
| (2.2.2) |
що разом з (1.17) дає
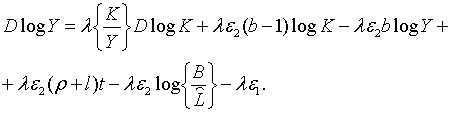
| (2.2.3) |
Маємо також

| (2.2.4) | 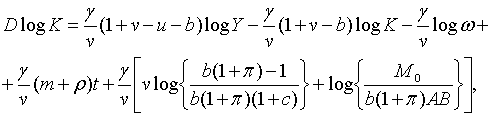
| (2.2.5) |
що ідентично (1.16) та (1.15) відповідно.
Траекторії зміни  та та 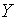 визначаються початковими значеннями змінних та системою рівнянь (2.2.3) —
(2.2.5). Ця система має частинний розв’язок:
де
визначаються початковими значеннями змінних та системою рівнянь (2.2.3) —
(2.2.5). Ця система має частинний розв’язок:
де
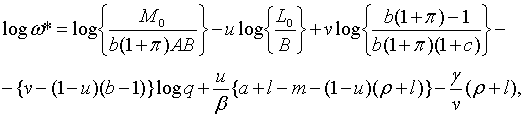
| (2.2.9) | 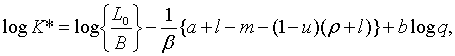
| (2.2.10) | 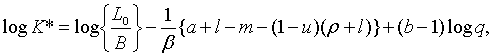
| (2.2.11) | 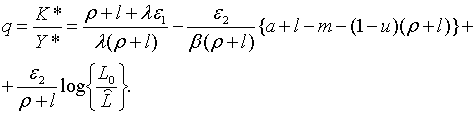
| (2.2.12) |
З (1.4), (2.27), (2.2.8), (2.2.10) та (2.2.11) випливає, що рівноважна
траекторія росту зайнятості визначається рівнянням:
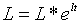
| (2.2.13) |
де
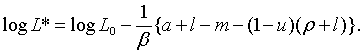 Відмітимо, що рівняння (2.2.13) тотожне (1.28) в тому розумінні, що
Відмітимо, що рівняння (2.2.13) тотожне (1.28) в тому розумінні, що 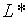 не залежить від
не залежить від 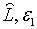 та та 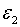 . Отже рівноважна траекторія росту зайнятості не залежить від оптимальної
траекторії і бюджетна політика яка визначена рівнянням (2.2.1), на неї не
впливає. Однак ця політика впливає на рівноважну траекторію росту випуску
продукції. Дійсно, із (2.2.11) випливає, що
. Отже рівноважна траекторія росту зайнятості не залежить від оптимальної
траекторії і бюджетна політика яка визначена рівнянням (2.2.1), на неї не
впливає. Однак ця політика впливає на рівноважну траекторію росту випуску
продукції. Дійсно, із (2.2.11) випливає, що 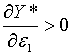 . Це пояснюється тиж, що ріст норми оподаткування (обумовлений зменншенням
державних позик в приватному секторі) або зниженням частки надходжень від
податків, направленою на покриття державних витрат, призводить до збільшення
рівноважного відношення капіталу до випуску продукції.
З рівнянь (2.2.3) — (2.2.5) та (2.2.9) — (2.2.12) отримаємо
де
. Це пояснюється тиж, що ріст норми оподаткування (обумовлений зменншенням
державних позик в приватному секторі) або зниженням частки надходжень від
податків, направленою на покриття державних витрат, призводить до збільшення
рівноважного відношення капіталу до випуску продукції.
З рівнянь (2.2.3) — (2.2.5) та (2.2.9) — (2.2.12) отримаємо
де
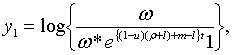
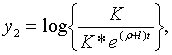
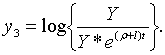 Точні траекторії зміни змінних
Точні траекторії зміни змінних 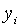 визначаються початковими значеннями цих змінних і системою рівнянь (2.2.14) —
(2.2.16), а наближені траекторії – тими ж початковими значеннями і системою
лінійних рівнянь, які включають (2.2.14), (2.2.15) та
визначаються початковими значеннями цих змінних і системою рівнянь (2.2.14) —
(2.2.16), а наближені траекторії – тими ж початковими значеннями і системою
лінійних рівнянь, які включають (2.2.14), (2.2.15) та
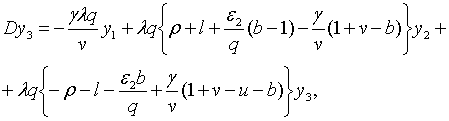
| (2.2.17) |
Характеристичними коренями матриці коефіцієнтів останньої системи є корені
рівняння
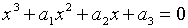 , ,
| (2.2.18) |
де
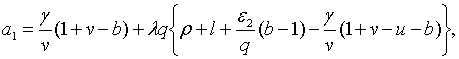
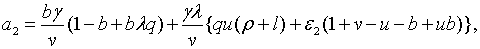
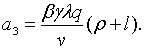 У співвідношення (2.2.1) яке описує вплив зворотнього зв’язку входять обидва
параметри політики
У співвідношення (2.2.1) яке описує вплив зворотнього зв’язку входять обидва
параметри політики 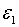 та
та 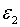 . Значення цих
параметрів впливає не тільки на стійкість системи, але і на рівноважне
відношення капітал — випуск. Припустимо, що бажанне значення . Значення цих
параметрів впливає не тільки на стійкість системи, але і на рівноважне
відношення капітал — випуск. Припустимо, що бажанне значення 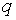 (яке являється рівноважним значенням відношення основного капіталу до випуску
продукції) визначається як окреме рішення прийнятої політики. При цьому
врахуємо, що рівноважна траекторія росту випуску буде тим вища, а початковий
рівень споживання тим нижчий, чим більше значення
(яке являється рівноважним значенням відношення основного капіталу до випуску
продукції) визначається як окреме рішення прийнятої політики. При цьому
врахуємо, що рівноважна траекторія росту випуску буде тим вища, а початковий
рівень споживання тим нижчий, чим більше значення 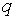 . Таким чином, розглядуючи вплив зміни
. Таким чином, розглядуючи вплив зміни 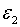 на стійкість системи будемо припускати що
на стійкість системи будемо припускати що 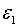 змінюється так, щоб значення
змінюється так, щоб значення 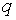 залишалося постійним. При цьому при диференційуванні функцій
залишалося постійним. При цьому при диференційуванні функцій 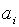 по
по 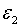 знак частинної
похідної використовується для того, щоб вказати, що сталою величиною є знак частинної
похідної використовується для того, щоб вказати, що сталою величиною є 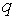 а не
а не 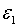 . Тепер,
припускаючи, що . Тепер,
припускаючи, що 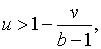 маємо
маємо 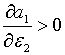 , , 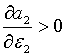 і при умові, що
і при умові, що 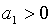 та та 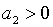 , похідна
, похідна 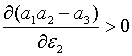 . Тобто
додатне значення . Тобто
додатне значення 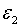 може здійснювати стабілізуючу дію.
Припустимо, наприклад, що задані такі значення праметрів:
може здійснювати стабілізуючу дію.
Припустимо, наприклад, що задані такі значення праметрів: 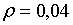 ;
; 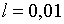 ; ; 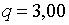 ;
; 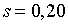 ; ; 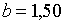 ;
; 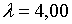 ; ; 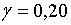 ;
; 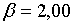 ; ; 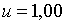 ;
; 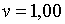 . Тоді, якщо . Тоді, якщо 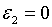 , корені (2.2.18) рівні:
, корені (2.2.18) рівні: 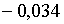 ;
; 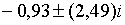 ; а якщо ; а якщо 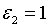 , вони рівні:
, вони рівні: 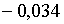 ; ; 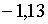 ;
; 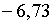 . Тобто, в цьому
випадку бюджетна політика призводить до ліквідації циклу і більш швидкої
збіжності до довгострокового тренду.
Надалі не розглядуються більш складні бюджетні політики, аналогічні грошовим
політикам, що описуються рівняннями (2.1.19) та (2.1.39). Це пояснюється тим,
що єдиними, що мають практичний зміст бюджетними політиками є ті, при яких
відношення заощаджень (особистих та державних) до національного доходу прямує
до додатньої константи при . Тобто, в цьому
випадку бюджетна політика призводить до ліквідації циклу і більш швидкої
збіжності до довгострокового тренду.
Надалі не розглядуються більш складні бюджетні політики, аналогічні грошовим
політикам, що описуються рівняннями (2.1.19) та (2.1.39). Це пояснюється тим,
що єдиними, що мають практичний зміст бюджетними політиками є ті, при яких
відношення заощаджень (особистих та державних) до національного доходу прямує
до додатньої константи при 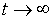 . Якщо це припущення справедливе, то жодна практично здійснювана бюджетна
політика не може здійснювати вплив на рівноважну траекторію росту зайнятості.
Хоча цей висновок очевидний з (2.2.13) і викладених щойно міркувань він може
здатися несподіваним, особливо, при співставленні з результатами, отриманими
змоделей, де грошові фактори не враховуються. На завершення цього розділу
наведемо неформальний опис впливу змін у бюджетній політиці, викликаючих
стійкій ріст відношення заощадження — доход. З цією метою ми будемо припускати,
що початковий стан економіки відповідає рівноважній траекторії росту.
Згадаємо, що в цьому розділі прийнято припущення що пропозиція грошей зростає в
геометричній прогресії, а отже бюджетні зміни не впливають на темп росту.
Звідци випливає, що надлишок надходжень від податків над поточними державними
витратами державних позик у приватного сектора економіки, а не для зменшення
пропозиції грошей. Тим не менш, зміни бюджетної політики вказаного типу одразу
викликає зменшення споживання, а отже і зайнятості. Але зменшення зайнятості, в
свою чергу викликає зниження пропорційного темпу росту заробітної плати та
цін, а в силу цього зменшення пропорційного темпу росту попиту на гроші.
Оскількі пропорційний темп росту пропозиції грошей не змінюється, норма
відсотка постійно падає, викликаючи поступове збільшення попиту на капітальні
товари та підвищення рівня зайнятості. Якщо значення
. Якщо це припущення справедливе, то жодна практично здійснювана бюджетна
політика не може здійснювати вплив на рівноважну траекторію росту зайнятості.
Хоча цей висновок очевидний з (2.2.13) і викладених щойно міркувань він може
здатися несподіваним, особливо, при співставленні з результатами, отриманими
змоделей, де грошові фактори не враховуються. На завершення цього розділу
наведемо неформальний опис впливу змін у бюджетній політиці, викликаючих
стійкій ріст відношення заощадження — доход. З цією метою ми будемо припускати,
що початковий стан економіки відповідає рівноважній траекторії росту.
Згадаємо, що в цьому розділі прийнято припущення що пропозиція грошей зростає в
геометричній прогресії, а отже бюджетні зміни не впливають на темп росту.
Звідци випливає, що надлишок надходжень від податків над поточними державними
витратами державних позик у приватного сектора економіки, а не для зменшення
пропозиції грошей. Тим не менш, зміни бюджетної політики вказаного типу одразу
викликає зменшення споживання, а отже і зайнятості. Але зменшення зайнятості, в
свою чергу викликає зниження пропорційного темпу росту заробітної плати та
цін, а в силу цього зменшення пропорційного темпу росту попиту на гроші.
Оскількі пропорційний темп росту пропозиції грошей не змінюється, норма
відсотка постійно падає, викликаючи поступове збільшення попиту на капітальні
товари та підвищення рівня зайнятості. Якщо значення 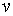 не дуже велике, рівень зайнятості прямує до рівноважного, в даному випадку до
початкового, рівня. Таким чино, єдиний стійкій ефект зміни бюджетної політики
зводиться до збільшення відношення накопичення капіталу до споживання, а отже
до підвищення рівноважної траекторії росту випуску продукції.
Наведений опис – спрощений, так як в ньому не враховано тимчасове запізнення
виробництва відносно попиту. Внаслідок цього запізнення траекторія збіжності,
як правило є коливальною, а не стійкою.
Поєднання грошової та бюджетної політики
В цьому розділі розрізнялися три мети здійснення кожної політики: 1)
досягнення оптимального довгострокового балансу між безробіттям та інфляцією;
2) досягнення оптимального довгострокового балансу між споживанням та
накопиченням капіталу; 3) мінімізація короткострокових флуктуацій. Було
показано, що при прийнятих в моделі припущеннях грошова політика може бути
використана для досягнення цілей 1) та 3) але не 2), а бюджетну політику, яка
належить до класу, що має практичний зміст можна використати для досягнення
цілей 2) і 3), але не 1). Отже, якщо прагнути досягнення всіх трьох цілей
необхідно застосовувати деяке поєднання грошової та бюджетної політик.
Ефективну систему регулювання економіки можна отримати, якщо об’єднати
політики, що описуються рівняннями (2.1.58) та (2.2.1). Для спрощення
викладок розглянемо комбіновану політику, що визначається рівняннями (2.1.39)
та (2.2.1). Тоді модель включає рівняння (1.1) — (1.9), (2.1.39) та (2.2.1).
Маємо рівняння
які ідентичні відповідно рівнянням (2.2.21), (2.1.41) та (2.1.42). Отримаємо
також, що
не дуже велике, рівень зайнятості прямує до рівноважного, в даному випадку до
початкового, рівня. Таким чино, єдиний стійкій ефект зміни бюджетної політики
зводиться до збільшення відношення накопичення капіталу до споживання, а отже
до підвищення рівноважної траекторії росту випуску продукції.
Наведений опис – спрощений, так як в ньому не враховано тимчасове запізнення
виробництва відносно попиту. Внаслідок цього запізнення траекторія збіжності,
як правило є коливальною, а не стійкою.
Поєднання грошової та бюджетної політики
В цьому розділі розрізнялися три мети здійснення кожної політики: 1)
досягнення оптимального довгострокового балансу між безробіттям та інфляцією;
2) досягнення оптимального довгострокового балансу між споживанням та
накопиченням капіталу; 3) мінімізація короткострокових флуктуацій. Було
показано, що при прийнятих в моделі припущеннях грошова політика може бути
використана для досягнення цілей 1) та 3) але не 2), а бюджетну політику, яка
належить до класу, що має практичний зміст можна використати для досягнення
цілей 2) і 3), але не 1). Отже, якщо прагнути досягнення всіх трьох цілей
необхідно застосовувати деяке поєднання грошової та бюджетної політик.
Ефективну систему регулювання економіки можна отримати, якщо об’єднати
політики, що описуються рівняннями (2.1.58) та (2.2.1). Для спрощення
викладок розглянемо комбіновану політику, що визначається рівняннями (2.1.39)
та (2.2.1). Тоді модель включає рівняння (1.1) — (1.9), (2.1.39) та (2.2.1).
Маємо рівняння
які ідентичні відповідно рівнянням (2.2.21), (2.1.41) та (2.1.42). Отримаємо
також, що
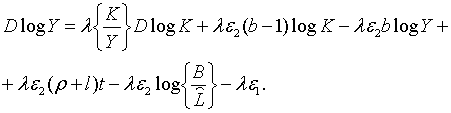
| (2.3.4) |
ідентичне (2.2.3)
Траекторії зміни змінних 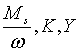 та
та 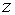 визначаються
початковими значеннями цих змінних та системою рівнянь (2.3.1) — (2.3.4).
Частинний розв’язок цієї системи визначаються
початковими значеннями цих змінних та системою рівнянь (2.3.1) — (2.3.4).
Частинний розв’язок цієї системи
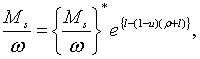
| (2.3.5) | 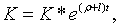
| (2.3.6) | 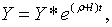
| (2.3.7) | 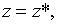
| (2.3.8) |
де
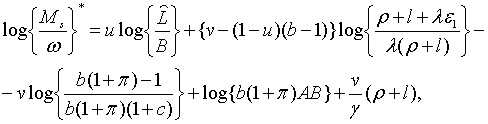
| (2.3.9) | 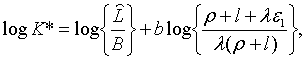
| (2.3.10) | 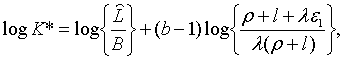
| (2.3.11) | 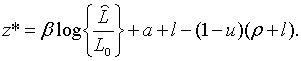
| (2.3.12) |
З (1.4), (2.3.6), (2.3.7), (2.3.10) та (2.3.11) випливає, шо рівноважна
траекторія росту зайнятості визначається рівнянням
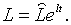
| (2.3.13) |
Отже, рівноважна і оптимальна траекторії зайнятості співпадають. Крім того з
(2.3.10) та (2.3.11) маємо
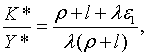
| (2.3.14) |
тобто рівноважне відношення основного капіталу до випусу залежить від 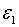 але не залежить від
але не залежить від 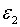 . Незалежність цього відношення від
. Незалежність цього відношення від 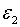 пояснюється рівністю рівноважного і оптимального пропорційних рівнів зайнятості.
Ці результати свідчать про те, що при використанні комбінованої грошової та
бюджетної політики, що визначається рівнянням (2.1.39) та (2.1.1) рівноважний
пропорційний рівень зайнятості та рівноважне відношення основного капіталу до
випуску продукції можна регулювати незалежно одне від одного, і що ці величини
не залежать від
пояснюється рівністю рівноважного і оптимального пропорційних рівнів зайнятості.
Ці результати свідчать про те, що при використанні комбінованої грошової та
бюджетної політики, що визначається рівнянням (2.1.39) та (2.1.1) рівноважний
пропорційний рівень зайнятості та рівноважне відношення основного капіталу до
випуску продукції можна регулювати незалежно одне від одного, і що ці величини
не залежать від 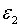 .
Розглянемо тепер співвідношення між стійкістю системи та значенням параметру .
Розглянемо тепер співвідношення між стійкістю системи та значенням параметру 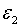 .
З рівнянь (2.3.1) — (2.3.4) та (2.3.9) — (2.3.12) отримуємо
.
З рівнянь (2.3.1) — (2.3.4) та (2.3.9) — (2.3.12) отримуємо
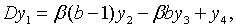
| (2.3.15) | 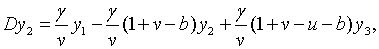
| (2.3.16) | 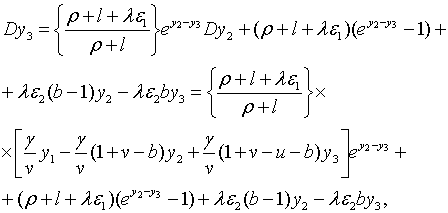
| (2.3.17) | 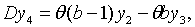
| (2.1.55) |
де
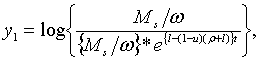
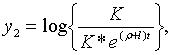
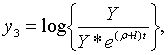
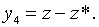 Точні траекторії зміни змінних
Точні траекторії зміни змінних 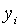 визначаються початковими значеннями цих змінних і системою рівнянь (2.3.15) —
(2.3.18), а наближені траекторії – тими ж початковими значеннями і системою
лінійних рівнянь, які включають (2.3.15), (2.3.16), (2.3.18) та
визначаються початковими значеннями цих змінних і системою рівнянь (2.3.15) —
(2.3.18), а наближені траекторії – тими ж початковими значеннями і системою
лінійних рівнянь, які включають (2.3.15), (2.3.16), (2.3.18) та
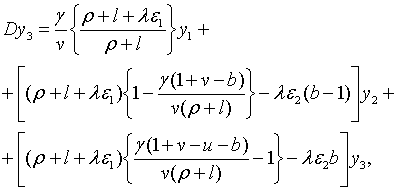
| (2.3.19) |
Характеристичними коренями матриці коефіцієнтів останньої системи є корені
рівняння
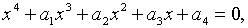
| (2.3.20) |
де
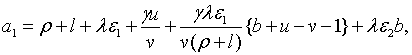
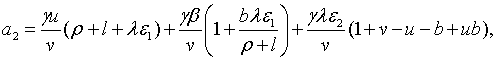
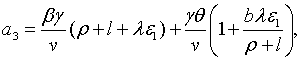
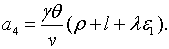 Зауважимо, що:
Зауважимо, що: 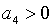 , , 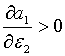 . Крім того, при умові
. Крім того, при умові 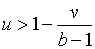 та
та 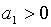 має місце
нерівність має місце
нерівність 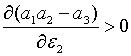 , а
якщо крім цього значення , а
якщо крім цього значення 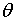 достатньо мале, виконується нерівність
достатньо мале, виконується нерівність 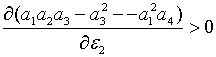 . Тобто, при додатньому
. Тобто, при додатньому 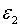 може мати місце стабілізуючий вплив.
Припустимо, наприклад, що
може мати місце стабілізуючий вплив.
Припустимо, наприклад, що 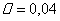 ;
; 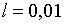 ; ; 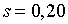 ;
; 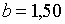 ; ; 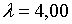 ;
; 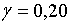 ; ; 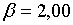 ;
; 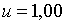 ; ; 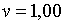 ,
, 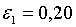 , , 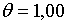 . При таких значеннях параметрів та при
. При таких значеннях параметрів та при 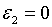 корені (2.3.20) рівні:
корені (2.3.20) рівні: 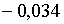 ;
; 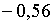 ; ; 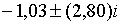 , а при
, а при 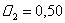 ці корені
рівні: ці корені
рівні: 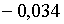 ; ; 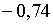 ;
; 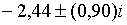 . Тобто, в цьому
випадку вплив додатнього значення параметра . Тобто, в цьому
випадку вплив додатнього значення параметра  проявляється якв збільшенні періода, так і в демпфуванні циклу, а також в більш
швидкій збіжності до довгострокового тренду.
проявляється якв збільшенні періода, так і в демпфуванні циклу, а також в більш
швидкій збіжності до довгострокового тренду.
Висновки
В кваліфікаційній роботі побудована математична модель економічної системи,
яка включає основні закономірності її функціонування. Створена програма,
дозволяє наглядно продемонструвати основні залежності економічних процесів.
Зокрема, можна побачити, зміна яких параметрів економічної системи веде до
інфляційних процесів. Також можна уточнювати параметри вибору фінансової
політики з метою одержання найкращіх результатів. Основним висновком, є
висновок про сильну взаємозалежність економічних показників між собою, і саме
він є предметом дослідження в даній роботі.
Страницы: 1, 2
|
|
|
|
|

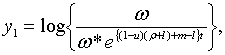
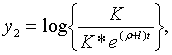
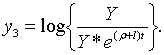 Точні траекторії зміни змінних
Точні траекторії зміни змінних 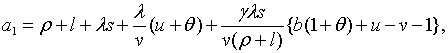
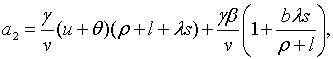
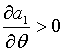 , і при умові, що
, і при умові, що 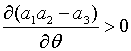 .
Отже, хоч політика задана рівнянням (2.1.1) не впливає на рівноважну траекторію
зайнятості (на відміну від політики, що передбачає постійну пропозицію грошей),
вона може справляти стабілізуючу дію.
Припустимо, наприклад, що
.
Отже, хоч політика задана рівнянням (2.1.1) не впливає на рівноважну траекторію
зайнятості (на відміну від політики, що передбачає постійну пропозицію грошей),
вона може справляти стабілізуючу дію.
Припустимо, наприклад, що 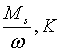 та
та 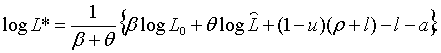 Крім того маємо
Крім того маємо
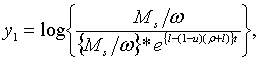
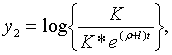
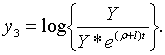 Точні траекторії
Точні траекторії 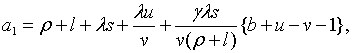
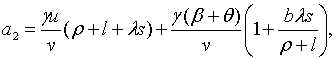
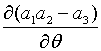 може
бути від’ємною. Цей результат демонструє, що політика (2.1.19) менш ефективна з
точки зору стабілізації системи, ніж політика (2.1.1).
Припустимо, наприклад, що
може
бути від’ємною. Цей результат демонструє, що політика (2.1.19) менш ефективна з
точки зору стабілізації системи, ніж політика (2.1.1).
Припустимо, наприклад, що 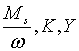 та
та 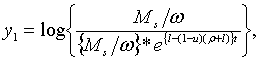
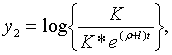
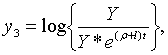
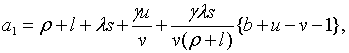
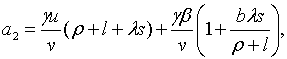
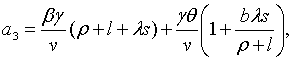
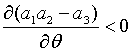 .
Відповідно, політика (2.1.39) може справляти дестабілізуючу дію.
Припустимо, наприклад, що
.
Відповідно, політика (2.1.39) може справляти дестабілізуючу дію.
Припустимо, наприклад, що 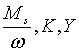 та
та 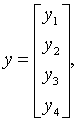
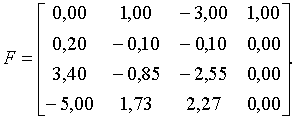 Характеристичні корені
Характеристичні корені 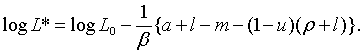 Відмітимо, що рівняння (2.2.13) тотожне (1.28) в тому розумінні, що
Відмітимо, що рівняння (2.2.13) тотожне (1.28) в тому розумінні, що 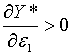 . Це пояснюється тиж, що ріст норми оподаткування (обумовлений зменншенням
державних позик в приватному секторі) або зниженням частки надходжень від
податків, направленою на покриття державних витрат, призводить до збільшення
рівноважного відношення капіталу до випуску продукції.
З рівнянь (2.2.3) — (2.2.5) та (2.2.9) — (2.2.12) отримаємо
. Це пояснюється тиж, що ріст норми оподаткування (обумовлений зменншенням
державних позик в приватному секторі) або зниженням частки надходжень від
податків, направленою на покриття державних витрат, призводить до збільшення
рівноважного відношення капіталу до випуску продукції.
З рівнянь (2.2.3) — (2.2.5) та (2.2.9) — (2.2.12) отримаємо
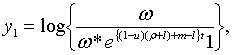
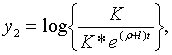
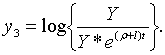 Точні траекторії зміни змінних
Точні траекторії зміни змінних 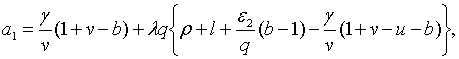
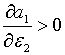 ,
, 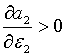 і при умові, що
і при умові, що 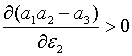 . Тобто
додатне значення
. Тобто
додатне значення 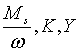 та
та 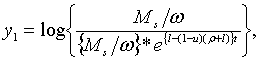
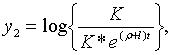
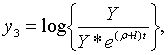
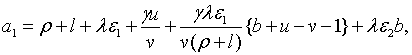
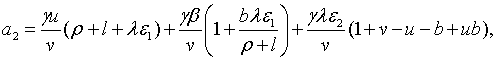
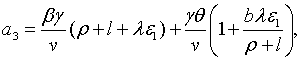
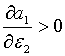 . Крім того, при умові
. Крім того, при умові 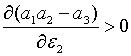 , а
якщо крім цього значення
, а
якщо крім цього значення 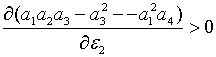 . Тобто, при додатньому
. Тобто, при додатньому