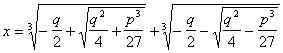Курсовая: Множина комплексних чисел

Курсовая: Множина комплексних чисел

Чернігівський державний педагогічний університет імені Т.Г.Шевченка

фізико-математичний факультет

Курсова робота на тему:

Множина комплексних чисел

Підготувала студентка 45 групи

Петрова Наталія Олександрівна

Чернігів 2003

План

1. Виникнення та розвиток поняття комплексного числа.

2. Поняття комплексного числа.

3. Дії над комплексними числами.

4. Геометричне зображення комплексного числа.

5. Модуль і аргумент комплексного числа.

6. Тригонометрична форма комплексного числа.

7. Застосування комплексних чисел.

Виникнення та розвиток поняття комплексного числа.

“Помимо и даже против воли того или другого математика, мнимые числа снова и

распространение”

Ф. Клейн.

Древнегреческие математики считали “настоящими” только натуральные числа.

Постепенно складывалось представление о бесконечности множества натуральных

чисел.

В III веке Архимед разработал систему обозначения вплоть до такого громадного

как . Наряду с

натуральными числами применяли дроби - числа, составленные из целого числа

долей единицы. В практических расчетах дроби применялись за две тысячи лет до

н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат

измерения всегда выражается или в виде натурального числа, или в виде отношения

таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил,

что “. элементы чисел являются элементами всех вещей и весь мир в целом

является гармонией и числом. Сильнейший удар по этому взгляду был нанесен

открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата

несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей

недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1.

Есть основание утверждать, что именно с этого открытия начинается эра

теоретической математики: открыть существование несоизмеримых величин с помощью

опыта, не прибегая к абстрактному рассуждению, было невозможно.

Следующим важным этапом в развитии понятия о числе было введение отрицательных

чисел - это было сделано китайскими математиками за два века до н. э.

Отрицательные числа применяли в III веке древнегреческий математик Диофант,

знавший уже правила действия над ними, а в VII веке эти числа уже подробно

изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью

отрицательных чисел можно было единым образом описывать изменения величин. Уже

в VIII веке было установлено, что квадратный корень из положительного числа

имеет два значения - положительное и отрицательное, а из отрицательных чисел

квадратный корень извлекать нельзя: нет такого числа

, чтобы .

В XVI веке в связи с изучением кубических уравнений оказалось необходимым

извлекать квадратные корни из отрицательных чисел. В формуле для решения

кубических уравнений вида

кубические и квадратные корни:

.

Эта формула безотказно действует в случае, когда уравнение имеет один

действительный корень (

), а если оно имеет три действительных корня (

), то под знаком квадратного корня оказывалось отрицательное число. Получалось,

что путь к этим корням ведет через невозможную операцию извлечения квадратного

корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й

степени, математики усиленно искали формулу для решения уравнения 5-й степени.

Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное

уравнение пятой степени

нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные

величины a, b, c, d, e с помощью шести алгебраических действий (сложение,

вычитание, умножение, деление, возведение в степень, извлечение корня).

В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень

которого больше чем 4, нельзя решить алгебраически. Тем не менее всякое

уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней

(среди которых могут быть и равные). В этом математики были убеждены еще в

XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на

рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.

Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой

природы. Он показал, что система уравнений

, не имеющая решений во множестве действительных чисел, имеет решения вида

, , нужно только

условиться действовать над такими выражениями по правилам обычной алгебры и

считать что .

Кардано называл такие величины “чисто отрицательными” и даже “

софистически отрицательными”, считал их бесполезными и старался их не

употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат

измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в

1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были

установлены первые правила арифметических операций над такими числами, вплоть

до извлечения из них кубических корней. Название “мнимые числа” ввел в

1637 году французский математик и философ Р. Декарт, а в 1777 году один из

крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую

букву французского слова imaginaire (мнимый) для обозначения числа

(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу

. Термин “комплексные числа” так же был введен Гауссом в 1831 году.

Слово комплекс (от латинского complexus) означает связь, сочетание,

совокупность понятий, предметов, явлений и т. д. Образующих единое целое.

В течение XVII века продолжалось обсуждение арифметической природы мнимых

чисел, возможности дать им геометрическое обоснование.

Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и

XVIII веков была построена общая теория корней n-ых степеней сначала из

отрицательных, а за тем из любых комплексных чисел, основанная на следующей

формуле английского математика А. Муавра (1707):

. С помощью этой формулы можно было так же вывести формулы для косинусов и

синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу :

, которая связывала воедино показательную функцию с тригонометрической. С

помощью формулы Л. Эйлера можно было возводить число e в любую

комплексную степень. Любопытно, например, что

. Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких

чисел, то есть строить теорию функций комплексного переменного.

В конце XVIII века французский математик Ж. Лагранж смог сказать, что

математический анализ уже не затрудняют мнимые величины. С помощью мнимых

чисел научились выражать решения линейных дифференциальных уравнений с

постоянными коэффициентами. Такие уравнения встречаются, например, в теории

колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский

математик Я. Бернулли применял комплексные числа для решения интегралов.

Хотя в течение XVIII века с помощью комплексных чисел были решены многие

вопросы, в том числе и прикладные задачи, связанные с картографией,

гидродинамикой и т. д., однако еще не было строго логического обоснования

теории этих чисел. По этому французский ученый П. Лаплас считал, что

результаты, полученные с помощью мнимых чисел, - только наведение,

приобретающее характер настоящих истин лишь после подтверждения прямыми

доказательствами.

“Никто ведь не сомневается в точности результатов, получаемых при вычислениях

с мнимыми количествами, хотя они представляют собой только алгебраические

формы иероглифы нелепых количеств” Л. Карно.

В конце XVIII века, в начале XIX века было получено геометрическое истолкование

комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс

независимо друг от друга предложили изобразить комплексное число

точкой на

координатной плоскости. Позднее оказалось, что еще удобнее изображать число не

самой точкой M, а вектором

, идущим в эту точку из начала координат. При таком истолковании сложение и

вычитание комплексных чисел соответствуют эти же операции над векторами. Вектор

можно задавать не только его координатами a и b, но так же длиной r и углом

 который он образует с положительным направлением

оси абсцисс. При этом

, и число z

принимает вид ,

который называется тригонометрической формой комплексного числа. Число r

называют модулем комплексного числа z и обозначают

. Число называют

аргументом z и обозначают ArgZ. Заметим, что если

, значение ArgZ не определено, а при

оно определено с точностью до кратного

. Упомянутая ранее формула Эйлера позволяет записать число z в виде

(показательная форма комплексного числа).

Геометрическое истолкование комплексных чисел позволило определить многие

понятия, связанные с функцией комплексного переменного, расширило область их

применения.

Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с

величинами, которые изображаются векторами

на плоскости: при изучении течения жидкости, задач теории упругости.

После создания теории комплексных чисел возник вопрос о существовании

“гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую

систему вида , где

, построил в 1843 году ирландский математик У. Гамильтон, который назвал их

“кватернионами”.

Большой вклад в развитие теории функций комплексного переменного внесли

русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к

упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н.

Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.

Поняття комплексного числа.

“Подобно тому, как всю область действительных величин можно представить с

величину a+ib”.

Гаусс

Рассмотрим множество чисел, каждое из которых определяется упорядоченной парой

дей­ствительных чисел. Действительные числа будем обозначать буквами а, b, с,

..., а упорядоченные пары действительных чисел — буквами α, β,

γ, ... и соот­ветственно записывать α=(a, b), β =(c, d) и т. д.

Такую упорядоченную пару действительных чисел (a,b) назовем комплексным

числом.

Определим действия над упорядоченными парами действительных чисел. Суммой

двух упорядоченных пар α= (а, b) и β = (с, d) назовем упорядоченную

пару γ = (a+c, b+d):

(a, b) + (c, d) = (a + c, b + d),

(1)

а произведением указанных пар — упорядоченную пару δ = (ас – bd, ad + bc):

(a, b)(c, d) = (ac – bd, ad + bc). (2)

Действия сложения и умножения упорядоченных пар действительных чисел

определены аксиома­тически.

Для этих действий существуют обратные дей­ствия — вычитание и деление (кроме

деления на нуль). Разностью α — β двух упорядоченных пар

α = (a, b) и β = (с, d) назовем такую упорядочен­ную пару (х, y), для

которой (с, d) + (x, y) = (a, b). Принимая во внимание равенство (1), получаем

с + х = a, d + y = b, откуда x = а – c, y = b – d. Разностью α — β

упорядоченных пар α = (а, b) и β = (с, d) является упорядоченная

пара (а – c, b – d):

(a, b) – (c, d) = (a – c, b – d). (3)

Нулем служит пара 0 = (0, 0). Упорядоченной парой, противоположной для

упорядоченной пары α = (а, b) будет, пара - α = ( -а, -b), так как

α + (-α) = (а, b) + (-а, -b) = (0,0) = 0.

Частным от деления упорядоченной пары α = (а, b) на упорядоченную

пару β = (с, d), где β

0 или с + d

0 (т. е. хотя бы одно из чисел с, d отлично от нуля) должна быть упорядоченная

пара (x, y) такая, что (с, d) (x, y) = (а, b). Отсюда на основании равенства

(2) получаем cx – dy = a, cy – dx = b. Из этой системы уравнений находим x и y:

x = , y = .

Итак, если β0,

то частное α/β двух упорядоченных пар α = (а, b), β = (с,

d) существует и определя­ется формулой:

= . (4)

Положив в этой формуле β = α (т. е. c = a, d = b), найдем, что

единицей при умножении упорядоченных пар служит упорядоченная пара (1, 0).

Полагая α = 1 = (1, 0), из формулы (4) получаем, что при β

0 упорядоченной парой, обратной для β, будет упорядоченная пара

.

Таким образом, построено множество чисел, дей­ствия над которыми определяются по

формулам (1) - (4). Это множество чисел называют множест­вом комплексных

чисел.

Докажем, что множество комплексных чисел в качестве своего подмножества

содержит все дейст­вительные числа. Рассмотрим упорядоченные пары вида (a,

0). Каждой паре (a, 0) поставим в соот­ветствие действительное число а, в

результате полу­чим взаимно однозначное соответствие между мно­жеством

рассматриваемых упорядоченных пар и множеством всех действительных чисел.

Применяя к указанным упорядоченным парам формулы (1) и (2), находим;

(а, 0) + (b, 0) = (а + b, 0); (а, 0) (b, 0) = (ab, 0).

Эти равенства означают, что упорядоченные пары вида (а, 0) складываются и

умножаются так же, как действительные числа. Следовательно, множест­во

указанных упорядоченных пар действительных чисел, рассматриваемое как

подмножество множест­ва комплексных чисел, по своим алгебраическим свойствам

не отличается от множества действитель­ных чисел. Это позволяет положить

(а, 0) = а, (5)

т. е. не различать упорядоченную пару (a, 0) дейст­вительных чисел и

действительное число a. В част­ности, нуль (0, 0) и единица (1, 0) множества

комп­лексных чисел оказываются обычными действитель­ными числами 0 и 1.

Покажем, что среди комплексных чисел содер­жится корень уравнения х

+ 1 = 0. Корнем уравне­ния х

+ 1 = 0 является такое число, квадрат кото­рого равен действительному числу —1.

Это число определяется упорядоченной парой (0, 1). В самом деле, применив

формулу (2), получим

(0, 1) (0, 1) = (-1, 0) = -1.

Обозначим эту упорядоченную пару через i, т. е. i = (0, 1), тогда

i = - 1, i = , (6)

число ί называют мнимой единицей.

Найдем произведение действительного числа b на упорядоченную пару (0, 1) =

ί — мнимую еди­ницу:

bi = (b, 0)(0, 1) = (0, b), ib = (0, 1)(b,

0) = (0, b). (7)

Если (а, b) - произвольная упорядоченная пара, то из очевидного равенства (а,

b) = (a, 0) + (0, b) и формул (5), (7) получаем

(a, b) = a + bi. (8)

Следовательно, комплексное число α = (a, b) мо­жет быть записано в виде a +

bi = a + ib, где a и b — действительные числа, ί —

мнимая единица, определяемая соотношением (6). Выражение a + bi называют

алгебраической формой комплексного числа. Число a называют

действительной, число b — мнимой частью комплексного числа a + bi.

Обозначая комплексное число a + bi одной буквой α, пишут:

a = Reα, b = Imα,

где Re — начальные буквы латинского слова realis (действительный), Im -

начальные буквы латинского слова imaginarius (воображаемый). Кроме

указанных обозначений, употребляются также и такие: a = R(α), b =

I(α), где (a, b) = a + bi. Числа вида bi называют чисто

мнимыми числами или просто мнимыми.

85

Комплексное число a + bi считают равным нулю тогда и только тогда, когда

а = 0, b = 0:

. (9)

Два комплексных числа a + bi и c + di считают равными

тогда и только тогда, когда равны между собой соответственно их действительные и

мнимые части, т. е. a = с, b = d:

. (10)

Комплексное число a - bi называют сопряжен­ным комплексному числу

a + bi. Обозначим число a - bi буквой

= a + bi. Числу

будет сопряжено число a – (-bi) = a + bi = α. Вследствие

этого числа α = a + bi и

= a - bi называют комп­лексно сопряженными числами.

Действительные числа и только они сопряжены сами себе. В самом деле, если

α = a, где a - действительное число, то из формул (5) и (8) имеем: α

= a + 0i = a,

= a – 0i = a, т. е. α =

.

Например: комплексному числу 3 + 5i сопряжённым будет 3 – 5i ;

комплексному числу 4 - 7i сопряжённым будет 4 + 7i .

Действия над комплексными числами, заданными в алгебраической форме

Рассмотрим правила, по которым производятся арифметические действия над

комплекс­ными числами.

Если даны два комплексных числа α = a + bi и β = c + di, то

α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,

α – β = (a + bi) – (c + di) = (a – c) + (b – d)i

. (11)

Это следует из определения действий сложения и вычитания двух упорядоченных пар

действительных чисел (см. формулы (1) и (3)). Мы получили правила сложения и

вычитания комплексных чисел: чтобы сложить два комплексных числа, надо

отдельно сложить их действительные части и соответственно мни­мые части; чтобы

из одного комплексного числа вычесть другое, необходимо вычесть

соответственно их действительные и мнимые части.

Число – α = – a – bi называют противополож­ным числу α

= a + bi . Сумма двух этих чисел равна нулю: - α + α = (- a -

bi) + (a + bi) = (-a + a) + (-b + b)i = 0.

Для получения правила умножения комплексных чисел воспользуемся формулой

(6), т. е. тем, что i2 = -1. Учитывая это соотношение,

находим (a + bi)( c + di) = ac + adi + bci + bdi

2 = ac + (ad + bc)i – bd, т.е.

(a + bi)( c + di) = (ac - bd) + (ad + bc)i . (12)

Эта формула соответствует формуле (2), которой определялось умножение

упорядоченных пар дей­ствительных чисел.

Отметим, что сумма и произведение двух комп­лексно сопряженных чисел являются

действительными числами. В самом деле, если α = a + bi,

= a – bi, то α

= (a + bi)( a - bi) = a2 – i2b2

= a2 + b2 , α +

= ( a + bi) + (a - bi) = (a + a) + (b - b)i = 2a, т.е.

α + = 2a,

α = a2

+ b2. (13)

При делении двух комплексных чисел в алгеб­раической форме следует

ожидать, что частное вы­ражается также числом того же вида, т. е. α/β

= u + vi, где u, v

R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + b

i, β = c + di, причем β ≠ 0, т. е. c2 + d

2 ≠ 0. Послед­нее неравенство означает, что c и d одновременно в

нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу

(12) и вто­рое из равенств (13), находим:

.

Следовательно, частное двух комплексных чисел определяется формулой:

, (14)

соответствующей формуле (4).

С помощью полученной формулы для числа β = с + di можно найти

обратное ему число β-1 = 1/β. Полагая в формуле (14) а

= 1, b = 0, получаем

.

Эта формула определяет число, обратное данному комплексному числу, отличному

от нуля; это число также является комплексным.

Например: (3 + 7i) + (4 + 2i) = 7 + 9i;

(6 + 5i) – (3 + 8i) = 3 – 3i;

(5 – 4i)(8 – 9i) = 4 – 77i;

.

Свойства действий

над комплексными числами

Для любых комплексных чисел α = a + bi, β = с + di,

γ = e + fi выполняются следую­щие свойства действий сложения и

умножения:

1) α + β = β + α – переместительное (коммутатив­ное)

свойство сложения;

2) (α + β) + γ = α + (β + γ) – сочетательное

(ассоциативное) свойство сложения;

3) αβ = βα – переместительное (комму­тативное) свойство

умножения;

4) (αβ)γ = α(βγ) – сочетательное

(ассоциативное) свойство умножения;

5) (α + β)γ = αγ + βγ – распределительное

(дистри­бутивное) свойство умножения относительно сло­жения.

Докажем, например, первое и третье из этих свойств. По определению сложения

получаем

α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,

β + α = (c + di) + (a + bi) = (c + a) + (d + b)i =

(a + c) + (b + d)i = α + β,

так как с + a = a + с, d + b = b + d, т. е. для любых действительных чисел

выполняется переместительное (коммутативное) свойство сложения. Далее,

αβ = (a + bi)(c + di) = aс + adi + bci +

bdi2 = (ac - bd) + (ad + bc)i,

βα = (c + di) (a + bi) = сa + cbi + dai +

dbi2 = (ca - db) + (cb + da)i = (ac - bd) + (ad + bc)

i = αβ,

поскольку для любых действительных чисел ac = ca, bd = db, т. е. выполняется

перемести­тельное (коммутативное) свойство умножения.

Остальные свойства доказываются аналогично, с учетом соответствующих свойств

операций над дей­ствительными числами.

Таким образом, операции над комплексными числами подчиняются тем же законам,

что и опера­ции над действительными числами.

Возведение в степень комплексного числа.

Извлечение корня из комплексного числа

При возведении в степень комплексного числа пользуются формулой бинома Ньютона:

.

С помощью формулы бинома Ньютона получаем

.

В правой части этого равенства заменяют сте­пени мнимой единицы i их

значениями и приводят подобные члены. Рассмотрим, как выражаются эти степени.

Учитывая формулу i2 = - 1 , получаем i3 =

i2 ∙ i = -1 ∙ i = - i, i4

= i3 ∙ i = -i ∙ i = -i

2 = 1, i5 = i4 ∙ i = i, i6 =

i5 ∙ i = i2 = -1, i7 =

i6 ∙ i = -i, i8 = i7

∙i = - i2 = 1 и т. д. В общем виде полученный

результат можно записать так:

i4k = 1, i4k+1 = i, i4k+2 = -1, i4k+3 = - i (k = 0, 1, 2, .).

Например: (3 + 4i)2 = 32 + 2 ∙ 3

∙ 4i + (4i)2 = 9 + 24i + 16i2

= 9 + 24i – 16 = -7 + 24i;

(1 + i)3 = 1 + 3i + 3i2 + i3 = 1 + 3i – 3 – i = - 2 + 2i.

Переходим к извлечению квадратного корни из комплексного числа a + bi.

Квадратным корнем из комплексного числа называют такое комплексное число,

квадрат которого равен данному комплексно­му числу. Обозначим это комплексное

число через u + vi, т. е.

.

Последнее равенство перепишем в следующем виде:

u2 + 2uvi + v2i2 = a + bi, u2 – v2 + 2uvi = a + bi.

Учитывая определение равенства комплексных чисел (см. (10)), получаем

u2 – v2 = a, 2uv = b. (15)

Возведем в квадрат обе части каждого из этих равенств, сложим их, преобразуем

полученную левую часть и извлечем квадратный корень:

(u2 – v2)2 + 4u2v2 = a2 + b2, (u2 + v2)2 = a2 + b2, u2 + v2 = .

Это уравнение и первое из уравнений (15) дают возможность определить u2 и v2 :

. (16)

Из первого уравнения находим два значения u, отличающиеся друг от друга

только знаком, второе уравнение дает два значения v. Все эти значения будут

действительными, поскольку при любых a и b

.

Знаки u и v следует выбирать так, чтобы выполнялось второе из равенств (15). Это

дает две возможные комбинации значений u и v, т. е. два числа u1 + v

1i, u2 + v2i, отличающиеся знаком.

Следовательно, извлечение квадратного корня из комплексного числа всегда

возможно и дает два значения, отличающиеся друг от друга только знаком.

Например: пусть требуется извлечь квадратный корень из комплексного числа

3 — 4i, т. е. найти комплексное число u + vi такое, что (u + v

i)2 = 3 – 4i. В данном случае a = 3, b = -4, поэтому

уравнения (16) принимают вид

, .

Второе из равенств (15) запишется так: 2uv = - 4, uv =-2; это означает, что

соответствующие зна­чения u и v имеют разные знаки. Так как u2 = 4,

v2 = 1, то с учетом равенства uv = -2 находим, что u1 =

2, v1 = -1, u2 = -2, v2 = 1, т.е. 2 – i

и -2 + i – значения квадратного корня из комп­лексного числа 3 – 4

i.

Геометрическое изображение комплексного числа

(a,b)

(a,b)

Рис. 1

0

x

y

i

-i

1

-1

Всякое комплексное число α = a + bi мы можем изображать как точку на

плоскости с координатами a и b (рис. 1). Число α называют аффиксом

этой точки. Плоскость, точки которой изображают комплексные числа, называют

комплексной числовой плоскостью. Начало координат, которому соответствует

число 0, называют нулевой точкой. При таком изображении комплексных

чисел действительные числа изображаются точками оси абсцисс, точки же оси

ординат представляют чисто мнимые числа. Поэтому ось абсцисс называют

действительной осью, ось ординат – мнимой осью. Сопряженные

комплексные числа α и

изображаются точками, симметричными относительно действительной оси,

противоположные комплексные числа α и –α симметричны относительно

нулевой точки.

Комплексные числа и соответствующие им точки комплексной плоскости обозначают

буквой z и пишут z = x + iy, где x – действительная часть (x = Rez), y

– мнимая часть (y = Imz).

Модуль и аргумент комплексного числа

Комплексное число z = x + iy изобра­зим точкой z комплексной плоскости;

точка z имеет координаты (x, y). Рассмотрим радиус-вектор

этой точки (рис. 2). Модулем комплексного числа z называют длину г

радиус-вектора

данной точки. Модуль комплексного числа z обозначают через |z|. Следовательно,

по определению

r = |z|, |z|0.

(17)

Поскольку г =

(получено из формулы для расстояния между двумя точками на плоскости: 0 (0, 0) и

z (x, y)), то

|z| = . (18)

y

φ

A

z

- φ

Рис. 2

x

0

z

Эта формула выражает мо­дуль комплексного числа z = x + iy через его

действительную и мнимую часть. Формула (18) имеет простой геометрический смысл:

она выражает длину гипотенузы прямо­угольного треугольника с катетами |х| и |y|

(см. рис. 2).

z=|z|

Отметим, что модуль комплексного числа являет­ся неотрицательным

действительным числом.

Аргументом комплексного числа z = x + iy назы­вают величину

угла φ наклона радиус-вектора

к положительной полуоси Ox. Аргумент комплексного числа z обозначают так: Argz.

При изменении z этот угол может принимать любые действительные значения (как

положительные, так и отрицательные; последние отсчитываются по часо­вой

стрелке). Если модули двух комплексных чисел равны, а значения угла φ

отличаются друг от друга на 2π, или на число, кратное 2π, то точки,

соответст­вующие этим комплексным числам, совпадают; комп­лексные числа в этом

случае равны между собой. Следовательно, аргумент комплексного числа z имеет

бесконечное множество значений, отличающихся друг от друга на число, кратное

2π. Аргумент не опре­делен лишь для числа 0, модуль которого равен нулю:

Страницы: 1, 2