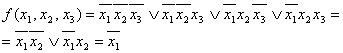|
|
|
|
Лекция: Минимизация функций алгебры логики
Лекция: Минимизация функций алгебры логики
Минимизация ФАЛ
Совершенно нормальные формы хотя и дают однозначные представления функции, но
являются очень громоздкими. Реализация СНФ программно или схемотехнически
является избыточной, что ведет к увеличению программного кода, поэтому
существуют методы упрощения логической записи – минимизации.
Определение: Преобразование логических функций с целью упрощения
их аналитического представления называются минимизацией.
Существуют два направления минимизации:
1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При
этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ.
2. Получение минимальной формы записи (цель – получение минимального числа
символов для записи всей функции сразу).
При этом следует учесть, что ни один из способов минимизации не универсален!
Существуют различные методы минимизации:
1. Метод непосредственных преобразований логических функций. (1.1)
При применении данного метода:
а) Записываются ДСНФ логических функций
б) Форма преобразуется и упрощается с использованием аксиом алгебры логики.
При этом, в частности, выявляются в исходном ДСНФ так называемые соседние
min-термы, в которых есть по одной не совпадающей переменной.
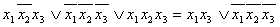 По отношению к соседним min-термам применяется закон склейки, значит ранг
min-терма понижается на единицу.
Определение: Min-термы, образованные при склеивании называются импликантами.
Полученные после склейки импликанты по возможности склеивают до тех пор, пока
склеивание становится невозможным.
Определение: Несклеивающиеся импликанты называются прослойками.
Определение: Формула, состоящая из простых импликант – тупиковая.
Пример:
По отношению к соседним min-термам применяется закон склейки, значит ранг
min-терма понижается на единицу.
Определение: Min-термы, образованные при склеивании называются импликантами.
Полученные после склейки импликанты по возможности склеивают до тех пор, пока
склеивание становится невозможным.
Определение: Несклеивающиеся импликанты называются прослойками.
Определение: Формула, состоящая из простых импликант – тупиковая.
Пример:
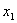
| 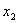
| 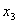
| 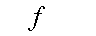
| 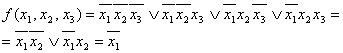
| | 0 | 0 | 0 | 1 | | 0 | 0 | 1 | 1 | | 0 | 1 | 0 | 1 | | 0 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | | 1 | 0 | 1 | 0 | | 1 | 1 | 0 | 0 | | 1 | 1 | 1 | 0 |
Если в процессе склейки образуется форма R, содержащая члены вида 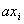 и
и 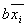 то для нее
справедливо выражение то для нее
справедливо выражение 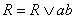 , что позволяет добавить к исходной форме R несколько членов вида пар
, что позволяет добавить к исходной форме R несколько членов вида пар 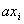 и
и 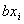 и после этого
продолжить минимизацию.
Пример: и после этого
продолжить минимизацию.
Пример:
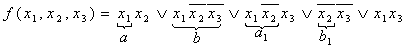

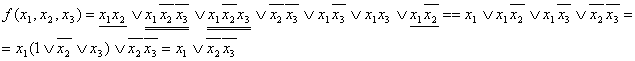 Мы получили минимальную СНФ.
Метод неопределенных коэффициентов. (1.2)
Суть метода состоит в преобразовании ДСНФ в МДНФ.
На основании теоремы Жигалкина любую ФАЛ можно представить в виде (рассмотрим
на примере трех переменных):
Мы получили минимальную СНФ.
Метод неопределенных коэффициентов. (1.2)
Суть метода состоит в преобразовании ДСНФ в МДНФ.
На основании теоремы Жигалкина любую ФАЛ можно представить в виде (рассмотрим
на примере трех переменных):
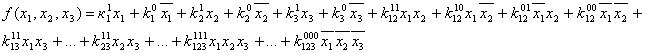 Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в
таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функции
Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в
таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функции 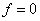 и приравнять все и приравнять все 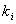 к нулю.
4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все
коэффициенты, встречающиеся в нулевых строках.
5. Проанализировать оставшиеся коэффициенты в единичных строках.
6. Используя правило, что дизъюнкция равна 1 если хотя бы один из к нулю.
4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все
коэффициенты, встречающиеся в нулевых строках.
5. Проанализировать оставшиеся коэффициенты в единичных строках.
6. Используя правило, что дизъюнкция равна 1 если хотя бы один из 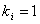 , выбрать min-термы минимального ранга. Причем отдавать предпочтение
коэффициентам, встречающимся в нескольких уравнениях одновременно.
7. Записать исходный вид функции.
Метод неопределенных коэффициентов применим для дизъюнктивной формы и
непригоден для конъюнктивной.
Пример:
, выбрать min-термы минимального ранга. Причем отдавать предпочтение
коэффициентам, встречающимся в нескольких уравнениях одновременно.
7. Записать исходный вид функции.
Метод неопределенных коэффициентов применим для дизъюнктивной формы и
непригоден для конъюнктивной.
Пример:
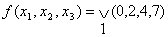
| 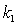
| 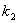
| 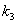
| 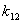
| 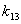
| 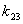
| 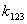
| 
| | 0 | 0 | 0 | 0 | 00 | 00 | 00 | 000 | 1 | | 1 | 0 | 0 | 1 | 00 | 01 | 01 | 001 | 0 | | 2 | 0 | 1 | 0 | 01 | 00 | 10 | 010 | 1 | | 3 | 0 | 1 | 1 | 01 | 01 | 11 | 011 | 0 | | 4 | 1 | 0 | 0 | 10 | 10 | 00 | 100 | 1 | | 5 | 1 | 0 | 1 | 10 | 11 | 01 | 101 | 0 | | 6 | 1 | 1 | 0 | 11 | 10 | 10 | 110 | 0 | | 7 | 1 | 1 | 1 | 11 | 11 | 11 | 111 | 1 |
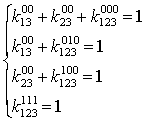 Итак, получим
Итак, получим 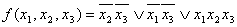 Метод Квайна (1.3)
Суть метода сводится к тому, чтобы преобразовать ДСНФ в МДНФ. Задачи
минимизации по методу Квайна состоит в попарном сравнении импликант, входящих
в ДСНФ с целью выявления возможности склеивания по какой-то пременной так:
Метод Квайна (1.3)
Суть метода сводится к тому, чтобы преобразовать ДСНФ в МДНФ. Задачи
минимизации по методу Квайна состоит в попарном сравнении импликант, входящих
в ДСНФ с целью выявления возможности склеивания по какой-то пременной так:
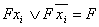 Таким образом, можно понизить ранг термов. Процедура производится до тех пор,
пока не остается ни одного терма, допускающего склейки с другим. Причем
склеивающиеся термы помечаются *.
Определение: Непомеченные термы называются первичными импликантами.
Полученное логическое выражение не всегда оказывается минимальным, поэтому
исследуется возможность дальнейшего упрощения.
Для этого:
1. Составляются таблицы, в строках которых пишутся найденные первичные
импликанты, а в столбцах указываются термы первичной ФАЛ.
2. Клетки этой таблицы отмечаются в том случае, если первичная импликанта
входит в состав какого-нибудь первичного терма.
3. Задача упрощения сводится к нахождению такого минимального количества
импликант, которые покрывают все столбцы.
Алгоритм метода Квайна (шаги):
1. Нахождение первичных импликант.
Исходные термы из ДНФ записывают в столбик и склеиваю сверху вниз.
Непомеченные импликанты переходят в функции на этом шаге.
2. Расстановка меток избыточности.
Составляем таблицу, в которой строки – первичные импликанты, столбцы –
исходные термы. Если некоторый min-терм содержит первичный импликант, то на
пересечении строки и столбца ставим метку.
3. Нахождение существенных импликант.
Если в каком-либо столбце есть только одна метка, то первичный импликант
соответствующей строки является существенным.
4. Строка, содержащая существенный импликант и соответствующие столбцы
вычеркиваются.
Если в результате вычеркивания столбцов появятся строки первичных импликант,
которые не содержат метки или содержат одинаковые метки в строках, то такие
первичные импликанты вычеркиваются. В последнем случае оставляем одну
меньшего ранга.
5. Выбор минимального покрытия.
Из таблицы, полученной на шаге 3 выбирают такую совокупность первичных
импликант, которая включает метки во всех столбцах по крайней мере по одной
метке в каждом. При нескольких возможных вариантах отдается предпочтение
покрытию с минимальным суммарным числом элементов в импликантах, образующих
покрытие.
6. Далее результат записывается в виде функции.
Пример:
Таким образом, можно понизить ранг термов. Процедура производится до тех пор,
пока не остается ни одного терма, допускающего склейки с другим. Причем
склеивающиеся термы помечаются *.
Определение: Непомеченные термы называются первичными импликантами.
Полученное логическое выражение не всегда оказывается минимальным, поэтому
исследуется возможность дальнейшего упрощения.
Для этого:
1. Составляются таблицы, в строках которых пишутся найденные первичные
импликанты, а в столбцах указываются термы первичной ФАЛ.
2. Клетки этой таблицы отмечаются в том случае, если первичная импликанта
входит в состав какого-нибудь первичного терма.
3. Задача упрощения сводится к нахождению такого минимального количества
импликант, которые покрывают все столбцы.
Алгоритм метода Квайна (шаги):
1. Нахождение первичных импликант.
Исходные термы из ДНФ записывают в столбик и склеиваю сверху вниз.
Непомеченные импликанты переходят в функции на этом шаге.
2. Расстановка меток избыточности.
Составляем таблицу, в которой строки – первичные импликанты, столбцы –
исходные термы. Если некоторый min-терм содержит первичный импликант, то на
пересечении строки и столбца ставим метку.
3. Нахождение существенных импликант.
Если в каком-либо столбце есть только одна метка, то первичный импликант
соответствующей строки является существенным.
4. Строка, содержащая существенный импликант и соответствующие столбцы
вычеркиваются.
Если в результате вычеркивания столбцов появятся строки первичных импликант,
которые не содержат метки или содержат одинаковые метки в строках, то такие
первичные импликанты вычеркиваются. В последнем случае оставляем одну
меньшего ранга.
5. Выбор минимального покрытия.
Из таблицы, полученной на шаге 3 выбирают такую совокупность первичных
импликант, которая включает метки во всех столбцах по крайней мере по одной
метке в каждом. При нескольких возможных вариантах отдается предпочтение
покрытию с минимальным суммарным числом элементов в импликантах, образующих
покрытие.
6. Далее результат записывается в виде функции.
Пример:
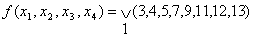 Шаг 1.
Шаг 1.
| Термы 4го ранга | Термы 3го ранга | Термы 2го ранга |  * 1 * 1
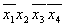 * 3 * 3
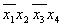 * 4 * 4
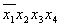 * 1 * 1
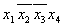 * 2 * 2
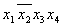 * 2 * 2
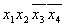 * 3 * 3
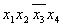 * 4 * 4
| 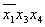
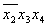
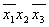 * 1 * 1
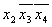 * 2 * 2
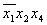
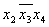 * 2 * 2
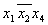
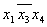
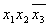 * 1 * 1
| 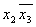
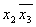
|
Шаг 2.
Шаг 4 пропускаем.
Шаг 5.
Выбираем те min-термы, при записи которых, МДНФ функции минимальна.
Шаг 6.
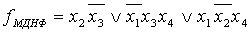 Недостаток метода Квайна – необходимость полного по парного сравнения всех
min-термов на этапе нахождения первичных импликант.
Идея модификации метода Квайна – метод Квайна-Мак-Класки. (1.4)
1. Каждая конъюнкция в ДСНФ представляется своим двоичным набором.
2. Вся совокупность номеров наборов разбивается на группы в зависимости от
числа единиц, имеющихся в номерах наборов (0-группа, 1-группа, 2-группа
и.т.д.).
3. Сравниваются две группы, отличающиеся на одну единицу.
4. В результате сравнения в номере набора, имеющего большее число единиц на
позиции, где обнаружится разница на одну единицу ставится прочерк.
5. В процессе преобразования возникают новые сочетания (n-группы).
6. Процесс преобразования длится до тех пор, пока возможна операция склеивания.
7. Элементы преобразованных групп являются первичными импликантами, которые
вместе с номерами исходных наборов образуют таблицы разметок.
8. В остальном эти методы совпадают с единственным уточнением – если в
результате таблицы разметок ни одна из строк не покрывает единицу столбца, то
надо выбрать номер столбца набора из предыдущей группы преобразований.
Определение: n-группа – это такой набор аргументов функции, что
число всех аргументов равных единице равно n, причем значении функции равно 1.
Пример:
Недостаток метода Квайна – необходимость полного по парного сравнения всех
min-термов на этапе нахождения первичных импликант.
Идея модификации метода Квайна – метод Квайна-Мак-Класки. (1.4)
1. Каждая конъюнкция в ДСНФ представляется своим двоичным набором.
2. Вся совокупность номеров наборов разбивается на группы в зависимости от
числа единиц, имеющихся в номерах наборов (0-группа, 1-группа, 2-группа
и.т.д.).
3. Сравниваются две группы, отличающиеся на одну единицу.
4. В результате сравнения в номере набора, имеющего большее число единиц на
позиции, где обнаружится разница на одну единицу ставится прочерк.
5. В процессе преобразования возникают новые сочетания (n-группы).
6. Процесс преобразования длится до тех пор, пока возможна операция склеивания.
7. Элементы преобразованных групп являются первичными импликантами, которые
вместе с номерами исходных наборов образуют таблицы разметок.
8. В остальном эти методы совпадают с единственным уточнением – если в
результате таблицы разметок ни одна из строк не покрывает единицу столбца, то
надо выбрать номер столбца набора из предыдущей группы преобразований.
Определение: n-группа – это такой набор аргументов функции, что
число всех аргументов равных единице равно n, причем значении функции равно 1.
Пример:
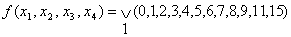 Составим таблицу истинности:
Составим таблицу истинности:
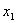
| 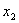
| 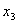
| 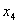
| 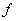
| | 0 | 0 | 0 | 0 | 1 | | 0 | 0 | 0 | 1 | 1 | | 0 | 0 | 1 | 0 | 1 | | 0 | 0 | 1 | 1 | 1 | | 0 | 1 | 0 | 0 | 1 | | 0 | 1 | 0 | 1 | 1 | | 0 | 1 | 1 | 0 | 1 | | 0 | 1 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | 1 | | 1 | 0 | 0 | 1 | 1 | | 1 | 0 | 1 | 0 | 0 | | 1 | 0 | 1 | 1 | 1 | | 1 | 1 | 0 | 0 | 0 | | 1 | 1 | 0 | 1 | 0 | | 1 | 1 | 1 | 0 | 0 | | 1 | 1 | 1 | 1 | 1 |
Запишем n-группы:
0-Группа: 0000
1-Группа: 0001, 0010, 0100, 1000
2-Группа: 0011, 0101, 0110, 1001
3-Группа: 0111,1011
4-Группа: 1111
Теперь сравним группы с номерами n и n+1:
0-Группа: 000-, 00-0, 0-00, -000
1-Группа: 00-1, 0-01, -001, 001-, 0-10, 010-,01-0, 100-
2-Группа: 0-11, -011, 01-1, 011-, 10-1
3-Группа: -111, 1-11
Еще раз сравним (при этом прочерки должны быть на одинаковых позициях):
0-Группа: 00--, 0-0-, -00-
1-Группа: 0--1, -0-1, 0-1-, 01—
2-Группа: --11
И еще раз сравним:
0-Группа: 0---
Запишем таблицу исходных min-термов, где функция равна 1:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1011 | 1111 | | | V | V | V | V | V | V | V | V | | | | | 0--- |
Выделим минимальное число групп, покрывающих
Для проверки составим таблицу истинности
| 1000 | 1001 | 1011 | 1111 | | -00- | V | V | | | | -0-1 | | V | V | | | -111 | | | V | V |
Метод минимизирующих карт (для ДСНФ и КСНФ). (1.5)
Одним из способов графического представления булевых функций от небольшого
числа переменных являются карты Карно. Их разновидность – карты Вейча,
которые строятся как развертки кубов на плоскости, при этом вершины куба
представляются клетками карты, координаты которых совпадают с координатами
соответствующих вершин куба.
Для ДСНФ единицы ставятся в клетке, соответствующей номеру набора, на котором
значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот.
Диаграмма для двух логических переменных (для ДСНФ):
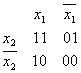 Для трех переменных:
Для трех переменных:
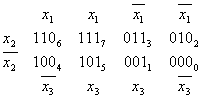 Карты Карно используются для ручной минимизации функций алгебры логики при
небольшом количестве переменных. Правило минимизации: склеиванию подвергаются
2,4,8,16,
Карты Карно используются для ручной минимизации функций алгебры логики при
небольшом количестве переменных. Правило минимизации: склеиванию подвергаются
2,4,8,16,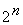 клеток и
клетки, лежащие на границе карты.
При числе переменных 5 и больше отобразить графически функцию в виде единой
плоской карты невозможно. Тогда строят комбинированные карты, состоящие из
совокупности более простых карт. Процедура минимизации заключается тогда в
том, что сначала находится минимальная форма 4-х мерных кубов (карт), а
затем, расширяя понятие соседних клеток, отыскивают min-термы для
совокупности карт. Причем соседними клетками являются клетки, совпадающие при
совмещении карт поворотом вокруг общего ребра.
Пример: Минимизировать ФАЛ от двух переменных: клеток и
клетки, лежащие на границе карты.
При числе переменных 5 и больше отобразить графически функцию в виде единой
плоской карты невозможно. Тогда строят комбинированные карты, состоящие из
совокупности более простых карт. Процедура минимизации заключается тогда в
том, что сначала находится минимальная форма 4-х мерных кубов (карт), а
затем, расширяя понятие соседних клеток, отыскивают min-термы для
совокупности карт. Причем соседними клетками являются клетки, совпадающие при
совмещении карт поворотом вокруг общего ребра.
Пример: Минимизировать ФАЛ от двух переменных: 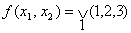
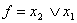 Минимизировать функцию:
Минимизировать функцию: 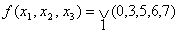
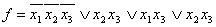 Минимизация логических функций, заданных в базисе
Минимизация логических функций, заданных в базисе 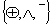 .
Метод неопределенных коэфициентов применим для минимизации функций, заданных в
различных базисах. Пусть функция .
Метод неопределенных коэфициентов применим для минимизации функций, заданных в
различных базисах. Пусть функция 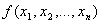 является ПСНФ, операция
является ПСНФ, операция 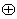 имеет особенности, отличающие ее от операции дизъюнкции.
1)
имеет особенности, отличающие ее от операции дизъюнкции.
1)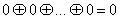 2)
2)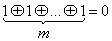 3)
3) 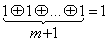 Минимизация при этом усложняется, так как ее основными критериями являются
минимальные ранги каждого терма и их минимальное количество, при этом в ходе
минимизации в базисе
Минимизация при этом усложняется, так как ее основными критериями являются
минимальные ранги каждого терма и их минимальное количество, при этом в ходе
минимизации в базисе 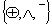 нецелесообразно приравнивать к нулю все коэффициенты на наборах где
нецелесообразно приравнивать к нулю все коэффициенты на наборах где 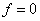 , т.к. в наборах, где функция
, т.к. в наборах, где функция 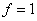 могут остаться термы высокого ранга. Поэтому особой разницы между выбором
нулевого или единичного значения функции нет.
Количество коэффициентов, остающихся в нулевых строках должно быть четным, а
в единичных – нечетным. Лучше всего рассматривать единичные строки и
оставлять те коэффициенты минимального ранга, которые чаще всего повторяются
в этих строках. В общем случае для получения минимальной формы выполняют
следующие действия:
1) Подсчитывают, сколько раз в единичных строках встречаются термы первого
ранга и оставляют из них те, которые встречаются максимальное число раз.
2) Находят нулевые строки, в которых встречаются оставленные в первом шаге
термы и их не обнуляют.
3) Рассматривая нулевую строку, в которой остался одни единичные термы и
находят в ней еще единичный терм, встречающийся максимальное число раз в
единичных строках, в которых еще не было оставлено ни одного терма и.т.д.
Метод Квайна-Мак-Класки может быть применим при минимизации этого базиса, при
этом кроме эффективных значений функции, где
могут остаться термы высокого ранга. Поэтому особой разницы между выбором
нулевого или единичного значения функции нет.
Количество коэффициентов, остающихся в нулевых строках должно быть четным, а
в единичных – нечетным. Лучше всего рассматривать единичные строки и
оставлять те коэффициенты минимального ранга, которые чаще всего повторяются
в этих строках. В общем случае для получения минимальной формы выполняют
следующие действия:
1) Подсчитывают, сколько раз в единичных строках встречаются термы первого
ранга и оставляют из них те, которые встречаются максимальное число раз.
2) Находят нулевые строки, в которых встречаются оставленные в первом шаге
термы и их не обнуляют.
3) Рассматривая нулевую строку, в которой остался одни единичные термы и
находят в ней еще единичный терм, встречающийся максимальное число раз в
единичных строках, в которых еще не было оставлено ни одного терма и.т.д.
Метод Квайна-Мак-Класки может быть применим при минимизации этого базиса, при
этом кроме эффективных значений функции, где 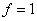 включаются некоторые min-термы, где
включаются некоторые min-термы, где 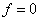 . Метод Квайна-Мак-Класки применим для минимизации базисов стрелки пирса и
штриха Шеффера.
Не полностью определенные ФАЛ (1.6)
Определение: не полностью определенные ФАЛ от n переменных
называется функции, заданные на множестве наборов меньше чем
. Метод Квайна-Мак-Класки применим для минимизации базисов стрелки пирса и
штриха Шеффера.
Не полностью определенные ФАЛ (1.6)
Определение: не полностью определенные ФАЛ от n переменных
называется функции, заданные на множестве наборов меньше чем 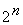 .
Если количество неопределенных наборов равно m то путем различных доопределений
можно получить
.
Если количество неопределенных наборов равно m то путем различных доопределений
можно получить 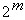 различных функций.
Пример: доопределить функцию
различных функций.
Пример: доопределить функцию 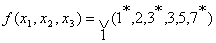 Где символ * означает "может быть".
Доопределим *=0
1)
Где символ * означает "может быть".
Доопределим *=0
1)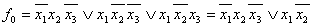 Доопределим *=1
2)
Доопределим *=1
2) 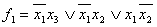 Если доопределять *=0 или *=1 то получим минимальный вариант:
3)
Если доопределять *=0 или *=1 то получим минимальный вариант:
3)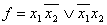 Пример показывает, что доопределение функции существенно влияет на конечный
результат минимизации. При доопределении
Пример показывает, что доопределение функции существенно влияет на конечный
результат минимизации. При доопределении 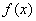 можно руководствоваться правилом: МДНФ не полностью определенных функций
получается как дизъюнкция наиболее коротких по числу букв импликант функции
можно руководствоваться правилом: МДНФ не полностью определенных функций
получается как дизъюнкция наиболее коротких по числу букв импликант функции 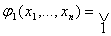 на всех наборах и функциях, которые в совокупности покрывают все импликативные
СНФ, и
на всех наборах и функциях, которые в совокупности покрывают все импликативные
СНФ, и 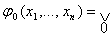 на всех
наборах, где функция не определена.
Пример: найти минимальную форму для на всех
наборах, где функция не определена.
Пример: найти минимальную форму для 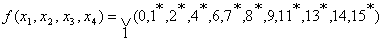 Составим таблицу истинности:
Составим таблицу истинности:
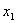
| 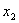
| 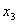
| 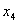
| 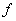
| | 0 | 0 | 0 | 0 | 1 | | 0 | 0 | 0 | 1 | * | | 0 | 0 | 1 | 0 | * | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 0 | * | | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | | 0 | 1 | 1 | 1 | * | | 1 | 0 | 0 | 0 | * | | 1 | 0 | 0 | 1 | 1 | | 1 | 0 | 1 | 0 | 0 | | 1 | 0 | 1 | 1 | * | | 1 | 1 | 0 | 0 | 0 | | 1 | 1 | 0 | 1 | * | | 1 | 1 | 1 | 0 | 1 | | 1 | 1 | 1 | 1 | * |
1) доопрделим *=1 и получим минимальный вид функции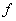
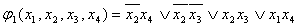 Доопрделим *=0
Доопрделим *=0
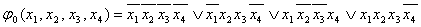 Оптимальное доопрделение функций соответствующее минимальному покрытию может
быть найдено по методу Квайна.
Оптимальное доопрделение функций соответствующее минимальному покрытию может
быть найдено по методу Квайна.
Страницы: 1, 2
|
|
|
|
|

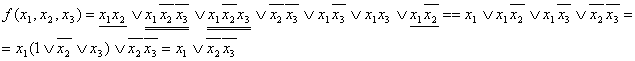 Мы получили минимальную СНФ.
Метод неопределенных коэффициентов. (1.2)
Суть метода состоит в преобразовании ДСНФ в МДНФ.
На основании теоремы Жигалкина любую ФАЛ можно представить в виде (рассмотрим
на примере трех переменных):
Мы получили минимальную СНФ.
Метод неопределенных коэффициентов. (1.2)
Суть метода состоит в преобразовании ДСНФ в МДНФ.
На основании теоремы Жигалкина любую ФАЛ можно представить в виде (рассмотрим
на примере трех переменных):
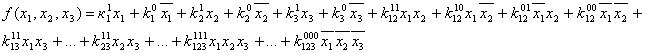 Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в
таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функции
Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в
таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функции 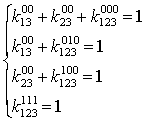 Итак, получим
Итак, получим 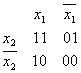 Для трех переменных:
Для трех переменных:
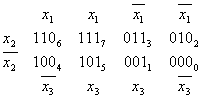 Карты Карно используются для ручной минимизации функций алгебры логики при
небольшом количестве переменных. Правило минимизации: склеиванию подвергаются
2,4,8,16,
Карты Карно используются для ручной минимизации функций алгебры логики при
небольшом количестве переменных. Правило минимизации: склеиванию подвергаются
2,4,8,16,