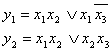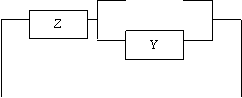|
|
|
|
Лекция: Минимизация функций алгебры логики
В результате получится минимальный вид функции вида: 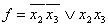 ее таблица единичных значений тогда будет:
ее таблица единичных значений тогда будет: 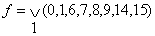 Временные булевы функции. (1.7)
Определение: Временная булева функция – логическая функция вида
Временные булевы функции. (1.7)
Определение: Временная булева функция – логическая функция вида 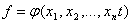 , принимающая значение единицы при
, принимающая значение единицы при 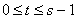 , где s – дискретное целочисленное значение, называемое автоматическим временем.
Утверждение: число различных временных булевых функций равно
, где s – дискретное целочисленное значение, называемое автоматическим временем.
Утверждение: число различных временных булевых функций равно 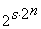 .
Доказательство: если функция времени принимает n значений .
Доказательство: если функция времени принимает n значений 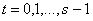 и на каждом интервале времени t соответствует
и на каждом интервале времени t соответствует 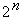 единичных наборов, то всего получится
единичных наборов, то всего получится 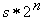 наборов, значит число временных булевых функций равно
наборов, значит число временных булевых функций равно 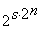 .
Любая временная булева функция может быть представлена в виде
.
Любая временная булева функция может быть представлена в виде 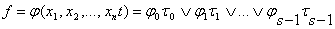 Где
Где 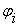 - конъюнктивный
или дизъюнктивный терм, а - конъюнктивный
или дизъюнктивный терм, а 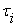 равно 0 или 1 в зависимости от времени t. Форма представления временных булевых
функций позволяет применить все метды минимизации.
Пример:
равно 0 или 1 в зависимости от времени t. Форма представления временных булевых
функций позволяет применить все метды минимизации.
Пример:
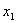
| 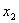
| 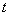
| 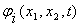
| | 0 | 0 | 0 | 0 | | 0 | 1 | 0 | 0 | | 1 | 0 | 0 | 1 | | 1 | 1 | 0 | 0 | | 0 | 0 | 1 | 0 | | 0 | 1 | 1 | 1 | | 1 | 0 | 1 | 1 | | 1 | 1 | 1 | 0 | | 0 | 0 | 2 | 0 | | 0 | 1 | 2 | 0 | | 1 | 0 | 2 | 1 | | 1 | 1 | 2 | 1 |
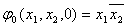
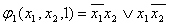
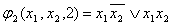
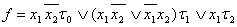 Временные булевы функции применяются для описания работы схем с памятью.
Определение: Производной первого порядка от булевой функции
Временные булевы функции применяются для описания работы схем с памятью.
Определение: Производной первого порядка от булевой функции 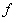 по переменной
по переменной 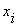 называется выражение:
называется выражение: 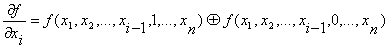 Где первая
Где первая 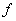 - единичная остаточная функция, а вторая- нулевая остаточная функция.
Пример: - единичная остаточная функция, а вторая- нулевая остаточная функция.
Пример:
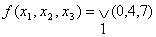 после минимизации получим: после минимизации получим:
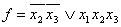
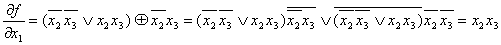 производная первого порядка по
производная первого порядка по 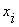 переменной определяет условие, при котором эта функция изменяет свое значение
при перемене значения
переменной определяет условие, при котором эта функция изменяет свое значение
при перемене значения 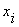 с 0 на 1.
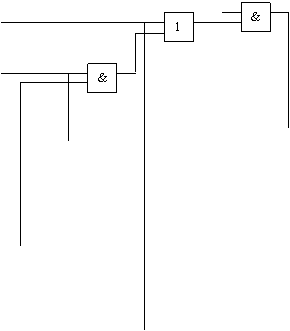
Для данной функции получим схему:
с 0 на 1.
Для данной функции получим схему:
 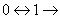 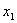
 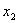 --- ---
 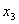 Смешанные производные k-го порядка.
Определение: смешанной производной k-го порядка называется выражение вида:
Смешанные производные k-го порядка.
Определение: смешанной производной k-го порядка называется выражение вида:
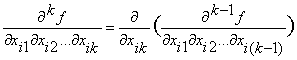 При этом порядок фиксированной переменной не имеет значения. Производная k-го
порядка
При этом порядок фиксированной переменной не имеет значения. Производная k-го
порядка 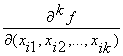 определяет условия, при которых эта функция изменяет свое значение при
одновременном изменении значений
определяет условия, при которых эта функция изменяет свое значение при
одновременном изменении значений 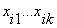 .
Согласно Бохману, производная k-го порядка вычисляется по формуле:
Пример: определить условия переключения выходного канала функции
.
Согласно Бохману, производная k-го порядка вычисляется по формуле:
Пример: определить условия переключения выходного канала функции 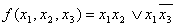 при переключении каждого канала, первого и второго канала, всех каналов
одновременно.
1)
при переключении каждого канала, первого и второго канала, всех каналов
одновременно.
1)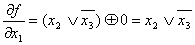
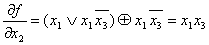
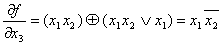
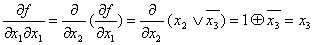
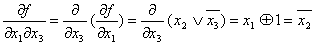
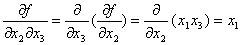
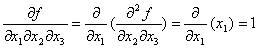
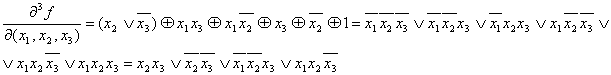 Понятие производной от булевых функций используется для синтеза логических
схем, а также в теории надежности.
Приложение алгебры логики. (1.8)
1) Для решения логических задач, - суть в том, что имея конкретные условия
логической задачи стараются записать их в виде ФАЛ, которые затем
минимизируют. Простейший вид формуды, как правило, приводят к ответу на
задачу.
Задача:
По подозрению в преступлению задержаны: Браун, Джон и Смит. Один – старик,
другой – чиновник, третий – мошенник). Все они дали показания, причем: старик
всегда говорил правду, мошенник всегда лгал, а чиновник иногда лгал, а иногда
говорил правду.
Показания: Браун – Я совершил это, Джон не виноват.
Джон – Браун не виноват, это сделал Смит.
Смит – я не виноват, виновен Браун.
На основании этого условия определить, кто из них совершил преступление, и
кто старик, кто мошенник и кто чиновник.
Обозначим буквами: Б- виноват Браун
Д – виноват Джон
С – виноват Смит
Тогда показания запишутся в виде:
Понятие производной от булевых функций используется для синтеза логических
схем, а также в теории надежности.
Приложение алгебры логики. (1.8)
1) Для решения логических задач, - суть в том, что имея конкретные условия
логической задачи стараются записать их в виде ФАЛ, которые затем
минимизируют. Простейший вид формуды, как правило, приводят к ответу на
задачу.
Задача:
По подозрению в преступлению задержаны: Браун, Джон и Смит. Один – старик,
другой – чиновник, третий – мошенник). Все они дали показания, причем: старик
всегда говорил правду, мошенник всегда лгал, а чиновник иногда лгал, а иногда
говорил правду.
Показания: Браун – Я совершил это, Джон не виноват.
Джон – Браун не виноват, это сделал Смит.
Смит – я не виноват, виновен Браун.
На основании этого условия определить, кто из них совершил преступление, и
кто старик, кто мошенник и кто чиновник.
Обозначим буквами: Б- виноват Браун
Д – виноват Джон
С – виноват Смит
Тогда показания запишутся в виде: 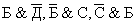 Тогда запишем функцию:
Тогда запишем функцию: 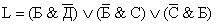 Запишем ее таблицу истинности и вычеркнем некоторые не подходящие наборы (2
преступника одновременно и.т.д.)
Запишем ее таблицу истинности и вычеркнем некоторые не подходящие наборы (2
преступника одновременно и.т.д.)
| Б | Д | С | 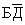
| 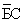
| 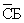
| L | | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |  2 2
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 5 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 6 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 7 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | | 8 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Значит Браун – чиновник, Джон – старик, Смит – мошенник, он же преступник.
2) Среди технических средств автоматизации (релейно-контактные системы).
Значительное место занимают РКС, используемые в вычислительной технике. РКС –
переключательные схемы. В 1910 г. физик Эрнфест указал на возможность
применения алгебры логики при исследовании РКС. Его идея заключается в том,
что каждой схеме можно сопоставить ФАЛ и наоборот. Это позволяет выявить
возможности схемы, изучая соответствующую формулу, а упрощение схемы свести к
упрощению ФАЛ – анализ переключательной схемы.
Синтез переключательной схемы (до построения схемы можно описать ее работу с
помощью логической функции).
Рассмотрим связь между переключательными схемами и ФАЛ. (1.8.1)
Определение: переключательная схема – схемотехническое изображение
устройства, состоящее из следующих элементов:
1) переключатель (может быть разомкнут или замкнут)
2) проводники
3) вход в схему и выход из нее
Примеры:
а) А В
б) Дизъюнкция: А В
в) Импликация: А В
г) Тождественно ложно: А
В
д) Тождественно истинно: А В
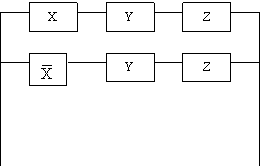
Из схем а,б,в можно получить функцию алгебры логики.
А
Б
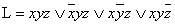 После упрощения получим:
А
B
После упрощения получим:
А
B
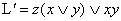 Синтез логической схемы. (1.8.2)
В зависимости от выходного сигнала, все электрические схемы можно разбить на
две группы:
1) 1-го рода – содержит комбинаторные схемы (выход зависит от входа)
2) 2-го рода – накапливающие схемы (элементы памяти, выход зависит от входа в
данный момент времени и в предыдущий момент времени).
По количеству входов и выходов делятся на:
1) 1+1 – 1 вход и 1 выход
2) n+1 – n входов и 1 выход
3) 1+n – 1 вход и n выходов
4) n+m – n входов и m выходов
Любая ЭВМ состоит из комбинации схем 1-го и 2-го порядков.
Определение: логический оператор схемы – это элементарная
логическая функция, с помощью которой описывается работа схемы в целом.
Анализ схемы производят в два этапа:
1) Из вспомогательной схемы удаляются все вспомогательные элементы, не
влияющие на логику работы системы.
2) Через логические операторы выражают все элементы схемы, получая логическое
уравнение, являющееся моделью функции, выполняемой схемой, затем ее упрощают
и переходят к схематическому изображению.
Примеры:
Простейшие логические схемы:
Синтез логической схемы. (1.8.2)
В зависимости от выходного сигнала, все электрические схемы можно разбить на
две группы:
1) 1-го рода – содержит комбинаторные схемы (выход зависит от входа)
2) 2-го рода – накапливающие схемы (элементы памяти, выход зависит от входа в
данный момент времени и в предыдущий момент времени).
По количеству входов и выходов делятся на:
1) 1+1 – 1 вход и 1 выход
2) n+1 – n входов и 1 выход
3) 1+n – 1 вход и n выходов
4) n+m – n входов и m выходов
Любая ЭВМ состоит из комбинации схем 1-го и 2-го порядков.
Определение: логический оператор схемы – это элементарная
логическая функция, с помощью которой описывается работа схемы в целом.
Анализ схемы производят в два этапа:
1) Из вспомогательной схемы удаляются все вспомогательные элементы, не
влияющие на логику работы системы.
2) Через логические операторы выражают все элементы схемы, получая логическое
уравнение, являющееся моделью функции, выполняемой схемой, затем ее упрощают
и переходят к схематическому изображению.
Примеры:
Простейшие логические схемы:
 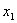
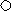
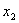 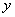
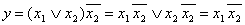 После упрощения получим:
После упрощения получим:
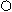 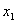
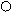
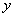
 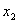 Синтез электронных схем (1.8.3)
Задачу синтеза электронных схем можно сформулировать следующим образом: при
заданных входных переменных и известной выходной функции, спроектировать
логическое устройство, которое реализует эту функцию. При этом могут быть
наложены дополнительные ограничения либо в виде системы логических элементов,
либо по количеству логических операторов и.т.д. Обычно, решая задачи анализа
и синтеза, используют полные базисы функций. При этом, любую логическую
функцию, входящую в базис, сопоставляют с некоторым физическим элементом, в
результате логическую схему можно заменить принципиальной схемой, состоящей
из физических элементов. Таким образом удается соединить математическую
задачу синтеза логической схемы с инженерной задачей проектирования
электронной схемы. При разработке электронной схемы за основные критерии
принимают минимум аппаратуры, минимум типов применяемых элементов и максимум
надежности. С точки зрения математической логики, задачи синтеза решаются при
обеспечении минимального числа логических операторов, минимального количества
типов логических операторов. В общем случае при синтезе электронной схемы
соблюдается следующая последовательность:
1) сопоставление математического описания, адекватно отображающего процессы,
происходящие в схеме (система логических уравнений).
2) анализ логических уравнений и получение минимальной формы для каждого из
них в заданном базисе.
3) переход от логических уравнений к логической схеме, посредством применения
логических операторов.
Электронные схемы с одним выходом.
Это наиболее простые схемы, основная сложность при синтезе этих схем – найти
выражение для выходной функции в заданном базисе.
Пример:
Синтез электронных схем (1.8.3)
Задачу синтеза электронных схем можно сформулировать следующим образом: при
заданных входных переменных и известной выходной функции, спроектировать
логическое устройство, которое реализует эту функцию. При этом могут быть
наложены дополнительные ограничения либо в виде системы логических элементов,
либо по количеству логических операторов и.т.д. Обычно, решая задачи анализа
и синтеза, используют полные базисы функций. При этом, любую логическую
функцию, входящую в базис, сопоставляют с некоторым физическим элементом, в
результате логическую схему можно заменить принципиальной схемой, состоящей
из физических элементов. Таким образом удается соединить математическую
задачу синтеза логической схемы с инженерной задачей проектирования
электронной схемы. При разработке электронной схемы за основные критерии
принимают минимум аппаратуры, минимум типов применяемых элементов и максимум
надежности. С точки зрения математической логики, задачи синтеза решаются при
обеспечении минимального числа логических операторов, минимального количества
типов логических операторов. В общем случае при синтезе электронной схемы
соблюдается следующая последовательность:
1) сопоставление математического описания, адекватно отображающего процессы,
происходящие в схеме (система логических уравнений).
2) анализ логических уравнений и получение минимальной формы для каждого из
них в заданном базисе.
3) переход от логических уравнений к логической схеме, посредством применения
логических операторов.
Электронные схемы с одним выходом.
Это наиболее простые схемы, основная сложность при синтезе этих схем – найти
выражение для выходной функции в заданном базисе.
Пример:
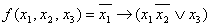 Типы логических элементов
Типы логических элементов 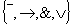 Надо привести в базис импликации
Надо привести в базис импликации 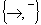 Т.к.
Т.к. 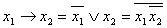 , то , то 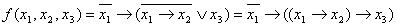 Тогда получим схему:
Тогда получим схему:
 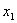
 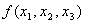
 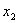

 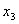 Задача синтеза, как правило, имеет различные решения в зависимости от выбора
системы логических элементов. Однако, для любой заданной ФАЛ почти всегда
можно синтезировать схему, соответствующую этой функции. Получение схемы с
минимальным количеством логических связок требует нахождения минимальной
формы для ФАЛ. Некоторые, более сложные схемы, имеющие несколько выходов,
могут быть сведены в частном случае к набору схем с одним выходом, тогда
синтез осуществляется путем декомпозиции для каждой выделенной схемы.
Пример: синтезировать схему одноразрядного двоичного сумматора методом
декомпозиции в базисе
Задача синтеза, как правило, имеет различные решения в зависимости от выбора
системы логических элементов. Однако, для любой заданной ФАЛ почти всегда
можно синтезировать схему, соответствующую этой функции. Получение схемы с
минимальным количеством логических связок требует нахождения минимальной
формы для ФАЛ. Некоторые, более сложные схемы, имеющие несколько выходов,
могут быть сведены в частном случае к набору схем с одним выходом, тогда
синтез осуществляется путем декомпозиции для каждой выделенной схемы.
Пример: синтезировать схему одноразрядного двоичного сумматора методом
декомпозиции в базисе 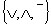 Составим таблицу истинности:
Составим таблицу истинности:
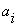
| 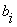
| 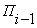
| 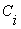
| 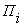
| | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 1 |
Где 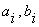 - переменные, - переменные, 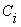 - сумма в
- сумма в 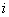 -ом
разряде, -ом
разряде, 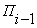 - перенос
из младшего разряда в старший, - перенос
из младшего разряда в старший, 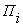 - перенос из старшего разряда.
Составим ДСНФ:
- перенос из старшего разряда.
Составим ДСНФ: 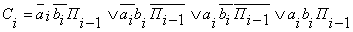
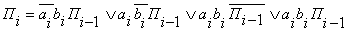 Тогда
Тогда 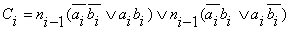
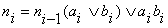
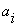 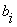 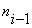
 Ci
Ci
 Пi
Такой способ не очень хорош, так как не всегда оптимален.
Электронные схемы с несколькими выходами (1.8.4)
Пусть n входов и k выходов.
Классический пример таких схем – дешифратор
Входы
Выходы
Пi
Такой способ не очень хорош, так как не всегда оптимален.
Электронные схемы с несколькими выходами (1.8.4)
Пусть n входов и k выходов.
Классический пример таких схем – дешифратор
Входы
Выходы
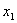
| 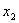
| 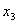
| 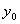
| 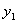
| 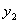
| 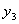
| 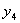
| 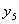
| 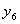
| 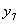
| | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Причем, например 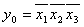 , а , а 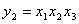 и.т.д. и.т.д.
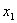 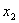 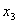
 y0
y0
 y7
y7
 Несложно убедиться, что такой подход не является оптимальным, поэтому
рассмотрим следующие моменты синтеза схем:
1) Классический основан на выделении простых импликант заданной системы
функций, подобно тому, как это делается в методе минимизации Квайна-Мак-
Класки, а затем ищется покрытие заданной функции этими импликантами.
При этом требуется:
1) найти простые импликанты заданной системы функций
2) выразить каждую функцию через простые импликанты
3) синтезировать схему, включающую только эти импликанты и связи между ними
Пример: синтезировать схему в базисе
Несложно убедиться, что такой подход не является оптимальным, поэтому
рассмотрим следующие моменты синтеза схем:
1) Классический основан на выделении простых импликант заданной системы
функций, подобно тому, как это делается в методе минимизации Квайна-Мак-
Класки, а затем ищется покрытие заданной функции этими импликантами.
При этом требуется:
1) найти простые импликанты заданной системы функций
2) выразить каждую функцию через простые импликанты
3) синтезировать схему, включающую только эти импликанты и связи между ними
Пример: синтезировать схему в базисе 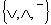 , функции которой на выходе имеют следующий вид:
, функции которой на выходе имеют следующий вид:
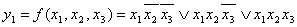
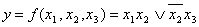 Решение: разобьем
Решение: разобьем 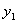 на группы, соответствующие по количеству единиц: на группы, соответствующие по количеству единиц:
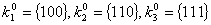
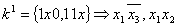
 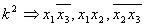
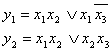
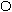
 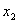 y2
y2
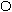
 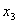 y1
y1
 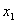 Метод каскадов (1.8.5)
Этот метод основан на разложении ФАЛ на k переменных:
Метод каскадов (1.8.5)
Этот метод основан на разложении ФАЛ на k переменных:
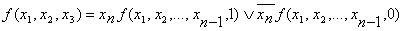 Где k
Где k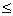 n
Эта формула попеременно применяется к заданной функции столько раз, чтобы
получить простое логическое выражение, которое легко синтезировать. n
Эта формула попеременно применяется к заданной функции столько раз, чтобы
получить простое логическое выражение, которое легко синтезировать.
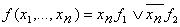
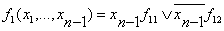
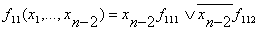 .
.
.
и.т.д.
Построенная на основе этих выражений логическая схема на каждом этапе
образует последний каскад искомой комбинационной схемы.
.
.
.
и.т.д.
Построенная на основе этих выражений логическая схема на каждом этапе
образует последний каскад искомой комбинационной схемы.
Страницы: 1, 2
|
|
|
|
|

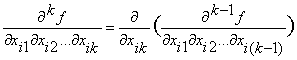 При этом порядок фиксированной переменной не имеет значения. Производная k-го
порядка
При этом порядок фиксированной переменной не имеет значения. Производная k-го
порядка 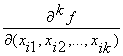 определяет условия, при которых эта функция изменяет свое значение при
одновременном изменении значений
определяет условия, при которых эта функция изменяет свое значение при
одновременном изменении значений 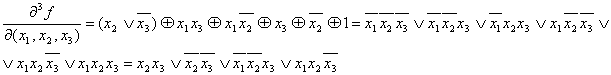 Понятие производной от булевых функций используется для синтеза логических
схем, а также в теории надежности.
Приложение алгебры логики. (1.8)
1) Для решения логических задач, - суть в том, что имея конкретные условия
логической задачи стараются записать их в виде ФАЛ, которые затем
минимизируют. Простейший вид формуды, как правило, приводят к ответу на
задачу.
Задача:
По подозрению в преступлению задержаны: Браун, Джон и Смит. Один – старик,
другой – чиновник, третий – мошенник). Все они дали показания, причем: старик
всегда говорил правду, мошенник всегда лгал, а чиновник иногда лгал, а иногда
говорил правду.
Показания: Браун – Я совершил это, Джон не виноват.
Джон – Браун не виноват, это сделал Смит.
Смит – я не виноват, виновен Браун.
На основании этого условия определить, кто из них совершил преступление, и
кто старик, кто мошенник и кто чиновник.
Обозначим буквами: Б- виноват Браун
Д – виноват Джон
С – виноват Смит
Тогда показания запишутся в виде:
Понятие производной от булевых функций используется для синтеза логических
схем, а также в теории надежности.
Приложение алгебры логики. (1.8)
1) Для решения логических задач, - суть в том, что имея конкретные условия
логической задачи стараются записать их в виде ФАЛ, которые затем
минимизируют. Простейший вид формуды, как правило, приводят к ответу на
задачу.
Задача:
По подозрению в преступлению задержаны: Браун, Джон и Смит. Один – старик,
другой – чиновник, третий – мошенник). Все они дали показания, причем: старик
всегда говорил правду, мошенник всегда лгал, а чиновник иногда лгал, а иногда
говорил правду.
Показания: Браун – Я совершил это, Джон не виноват.
Джон – Браун не виноват, это сделал Смит.
Смит – я не виноват, виновен Браун.
На основании этого условия определить, кто из них совершил преступление, и
кто старик, кто мошенник и кто чиновник.
Обозначим буквами: Б- виноват Браун
Д – виноват Джон
С – виноват Смит
Тогда показания запишутся в виде: