|
РУБРИКИ |
Реферат: Дифференциальные уравнения |
РЕКОМЕНДУЕМ |
||
|
Реферат: Дифференциальные уравненияподставим значения x=1, y=1, и найдем, отвечающее искомой кривой, значение постоянной Очевидно, это значение равно . Следовательно, искомое частное решение определяется уравнением Yx=1 или Пример 3. Рассмотрим уравнение , приведенное в параграфе 3. Разрешая его относительно y/, получаем два уравнения y/=1 и y/=-1 или и Оба являются с разделяющимися переменными и приводятся к виду dy=dx и dx=-dx. Интегрирование левых и правых частей уравнений дает следующие их общие решения y=x+c и y=-x+c. Пример 4. Следующим уравнением возьмем уарвнение Разрешая его относительно y/ получаем Разделяя переменные имеем Найдем интегралы от левой и правой частей уравнения: . Приравнивая интегралы и заменяя две постоянных на одну получаем следующий вид общего решения уравнения Возводя в квадрат обе части данного уравнения, получаем окончательный вид общего решения (x-c)2+y2=1. Пример 5. Решить дифференциальное уравнение Найти его частное решение при условии Разрешая уравнение относительно y/, видим, что оно является уравнением с разделяющимися переменными Разнося переменные по разные стороны уравнения получаем Интегрируя каждую из частей этого уравнения, получаем следующее общее решение исходного дифференциального уравнения Используя начальное условие , определяем значение константы c для искомого частного решения . Искомое частное решение дается уравнением . 6. Однородное дифференциальное уравнение первого порядка. Функция f(x,y) называется однородной степени m, если Функция f(x,y) называется однородной нулевой степени, если Например, функция . Функция Всякая однородная функция нулевой степени может быть представлена в виде функции от отношения y/x (или отношения x/y). Действительно, пусть f(x,y) – однородная функция нулевой степени, тогда, взяв в качестве , имеем может рассматриваться как функция отношения y/x, т.е. . Определение. Дифференциальное уравнение первого порядка F(x,y,y/)=0, называется однородным, если оно может быть представлено в виде y/ =f(x,y) или f(x,y) – однородная функция нулевой степени. Решение однородного дифференциального уравнения сводится к решению уравнения с разделяющимися переменными заменой y/x=u или y=ux, где u-функция от x. Подставляя в исходное уравнение и уравнение вида , являющиеся с разделяющимися переменными. Если u=g(x,c) или Ф(x,u,c)=0 является его общим решением, то y=xg(x,c) или Ф(x,y/x,c)=0 будет общим решением исходного уравнения. Пример 1. Рассматривается уравнение (x2-y2)dx+2xydy=0. Перепишем его в виде . Справа стоит функция однородная нулевой степени. Действительно, . Итак, преобразованное уравнение является однородным дифференциальным уравнением. Решаем его заменой y=ux. Получаем Разделяя переменные приходим к уравнению Интегрируем левую и правую части этого уравнения: Приравнивая найденные интегралы, получаем общее решение вспомогательного дифференциального уравнения относительно переменных x и u Потенциируя последнее выражение, общее решение получает вид , где c – произвольная постоянная. Заменяя u=y/x, получаем общий интеграл исходного дифференциального уравнения или y2+x2=cx, Последнее выражение приводится к виду Таким образом, семейством интегральных кривых исходного уравнения является семейство окружностей с центрами в точках , лежащих на оси x, и радиусами . Очевидно, все эти окружности касаются оси y в точке начала координат. На рис. 6 изображено семейство этих окружностей. Пример 2. Требуется найти частное решение уравнения Удовлетворяющих начальному условию y(1)=0. Нетрудно видеть (убедиться), что справа стоит однородная функция нулевой степени. Итак, исходное дифференциальное уравнение является однородным. Выполняя замену y=ux, приводим его к виду Разделяем переменные, получаем Интегрируя обе части этого уравнения, получаем общее решение вспомогательного дифференциального уравнения Подставим в него получим Логарифмируя обе части этого уравнения получаем и далее Последнее соотношение дает общее решение исходного дифференциального уравнения. Чтобы найти частное решение, воспользуемся начальными условиями x=1,y=0. Подставим их в общее решение , отсюда . Таким образом, искомое частное решение имеет вид 7. Линейное дифференциальное уравнение первого порядка. Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида y/+g(x)y=h(x). Такое название ему дано в связи с тем, что относительно переменных y и y/ его можно рассматривать как линейное. Если принимает простой вид y/=h(x), и сводится к нахождению неопределенного интеграла . Его общее решение тогда имеет вид . Если называется однородным линейным. Оно приобретает вид , и, как нетрудно видеть, сводится к решению уравнения с разделяющимися переменными и далее Его общее решение имеет вид Предположим теперь, что , функции g(x) и h(x) являются непрерывными. Пусть y=f(x,c) – искомое общее решение линейного дифференциального уравнения. Представим исходное уравнение в виде и подставим в выражение, стоящее в квадратных скобках, , т.е. как бы полагая в общем решении . Тогда вышеприведенное уравнение примет вид являясь линейным однородным дифференциальным уравнением (в нем вместо y взята для удобства переменная z, чтобы не возникло путаницы решений этого уравнения с исходным). Общее решение этого уравнения, как уже отмечалось ранее, может быть представлено в виде где A – произвольная постоянная. Очевидно, является его частным решением, и, следовательно, может быть получено при некотором значении , т.е. Если теперь освободиться от условия фиксирования постоянной , то получаем, что общее решение исходного уравнения имеет вид В нем второй множитель функция является, как нетрудно видеть, частным решением при c=1 однородного линейного уравнения множитель функция представляет общее решение дифференциального уравнения u/v(x)=h(x). Действительно, подставляя в это уравнение u/x(x,c), получаем тождество Таким образом, показано, что общее решение линейного дифференциального уравнения Представляется в виде y=u(x,c)v(x), где v(x) – частное решение однородного уравнения решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x). Нетрудно видеть, что в обоих случаях приходится решать уравнение с разделяющимися переменными. Заметим, что хотя при решении однородного уравнения бралось частное решение V(x) однородного уравнения v/+g(x)v=0, Являющегося уравнением с разделяющимися переменными. На втором этапе определяется решение u(x,c) дифференциального уравнения u/ v(x)=h(x), Также являющегося уравнением с разделяющимися переменными. После их решений общее решение исходного линейного уравнения представляется в виде Y=u(x,c)v(x). Пример 1. Решить уравнение Y/+2y=sinx. Сначала решаем однородное уравнение v/+2v=0. Из него получаем Интегрируя его левую и правую части, получаем его общий интеграл (решение) вида Полагая в нем c=0 и потенциируя его, получаем следующее его нетривиальное частное решение Далее решаем уравнение вида Разнося переменные в разные части уравнения и интегрируя их, получаем общее решение этого уравнения Вычислим интеграл: . Рассматривая данное уравнение, как уравнение относительно интеграла, находим его вид Следовательно, Тогда общее решение исходного уравнения будет Предположим теперь, что требуется выделить частное решение, проходящее через точку M(0,0), т.е. решение, удовлетворяющее начальному условию y(0)=0. Для этого подставим значения x=0, y=0 в общее решение и найдем соответствующее значение постоянной c: Искомым частным решением является Пример 2. Решить уравнение являющееся линейным дифференциальным уравнением. На первом этапе найдем решение соответствующего линейного однородного уравнения Разделяя переменные по разные стороны уравнения, имеем Интегрируя обе части данного уравнения, получаем следующее его частное решение На втором этапе решаем уравнение вида Делая замену сокращая обе части уравнения на и разделяя переменные, имеем du=x2dx. Интегрируя правую и левую части уравнения, получаем его общее решение Общее решение исходного дифференциального уравнения имеет вид 8. Дифференциальное уравнение первого порядка в полных дифференциалах. Определение. Пусть дифференциальное уравнение первого порядка представлено в виде M(x,y)dx+N(x,y)dx=0, Где M(x,y) и N(x,y) – функции двух переменных x и y. Тогда, если левая часть уравнения есть полный дифференциал некоторой функции U(x,y), т.е. dU(x,y)=M(x,y)dx+N(x,y)dy, то такое уравнение называется уравнением в полных дифференциалах. Уравнение в полных дифференциалах кратко можно представить в виде dU(x,y)=0, а поэтому общий интеграл (решение) такого уравнения имеет вид U(x,y)=0. Дифференциальное уравнение такого типа возникает, когда поведение системы подчинено условию сохранения некоторой величины U(энергии, массы, стоимости и т.д.). Отметим следующий признак, позволяющий определить является ли рассматриваемое уравнение уравнением в полных дифференциалах. Путьс dU(x,y)=M(x,y)dx+N(x,y)dy, тогда функции M(x,y) и N(x,y) должны быть для U(x,y) частными производными первого порядка, соответственно, по переменным x и y, т.е. Предполагая функции M(x,y) и N(x,y) непрерывными и имеющими непрерывные частные производные, соответственно, по y и x, т.е. выполнение соотношений из тождества получаем, что для M(x,y) и N(x,y) должно выполняться условие Полученное условие является не только необходимым, но и достаточным для того, чтобы уравнение M(x,y)dx+N(x,y)dy=0 Было уравнением в полных дифференциалах. Нахождение общего решения уравнения в полных дифференциалах проводится в два этапа. На первом этапе функция U(x,y) рассматривается как функция только аргумента x, переменная y получает как бы фиксированное значение . Тогда соотношению ставится в соответствие дифференциальное уравнение Пусть его общее решение представляется в виде Но так как решение уравнения зависит от y, то в общем решении постоянная c является функцией y, т.е. c=h(y). Следовательно, общее решение предыдущего дифференциального уравнения, снимая с y условие закрепления его значения, имеет вид U(x,y)=g(x,y)+h(y). На втором этапе находится вид функции h(y). Для этого обратимся к соотношению в котором уже закрепляется как бы значение переменной x. Используя данное соотношение и вид функции U(x,y), получаем дифференциальное уравнение, связывающее переменные h и y: Интегрируя это уравнение, находим его общее решение Из В последнем двойном интеграле вместо можно взять функцию (т.к. функция U(x,y) получает вид Так как общее решение исходного дифференциального уравнения записывается в виде U(x,y)=c=const, то, заменяя две постоянных на одну, получаем следующий вид общего решения уравнения Пример 1. Дано дифференциальное уравнение (6x2y2+6xy-1)dx+(4x3y+3x2y+2y)dy=0. В нем M(x,y)=6x2y2+6xy-1, N(x,y)=4x3y+3x2y+2y. Из Следует, что данное уравнение является уравнением в полных дифференциалах. Проведем его решение в два этапа. На первом решаем уравнение в котором переменная y считается закрепленной. Интегрируя это уравнение, получаем U(x,y)=2x3y2+3x2y-x+h(y). На втором этапе определяем вид функции h(y), используя для этого соотношение и дифференциальное уравнение для h и y 4x3y+3x2+h/(y)=4x3y+3x2+2y или Интегрируя последнее, получаем h=y2+c. Общий интеграл исходного уравнения тогда можно записать в виде 2x3y2+3x2y-x+y2=c. Пример 2. Найти решение уравнения 2xsinydx+(3y2+x2cosy)dy=0. Проверяем, является ли оно уравнением в полных дифференциалах? Для этого из M(x,y)=2xsiny, N(x,y)=3y2+x2cosy Находим Так как, очевидно, выполняется условие то уравнение есть уравнение в полных дифференциалах. Сначала решаем уравнение считая y постоянной. Интегрирование уравнения дает U(x,y)=x2siny+h(y). Затем находим функцию h(y), используя соотношения , с другой стороны. Соотношения приводят к дифференциальному уравнению Интегрируя последнее уравнение, получаем h=y3+c. Тогда общий интеграл исходного дифференциального уравнения записывается в виде X2siny+y3+c=0. Далее рассмотрим понятие интегрирующего множителя. Ранее отмечалось, что уравнение в полных дифференциалах возникает, когда поведение системы сохраняет некоторую величину U, т.е. удовлетворяет соотношению U(x,y)=c. Дифференциальным аналогом его является уравнение dU(x,y)=0 или M(x,y)dx+N(x,y)dy=0, Где Предположим теперь, что частные производные функции U(x,y) представимы в виде Тогда соотношению U(x,y)=e будет соответствовать уравнение в полных дифференциалах вида M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0. Если теперь данное уравнение разделить на общий множитель слагаемых g(x,y), то получим уравнение M(x,y)dx+N(x,y)dy=0. Решение последнего уравнения эквивалентно решению предыдущего, из которого оно получено, однако оно может уже не являться уравнением в полных дифференциалах, также для него возможно будет В то же время после умножения его на множитель g(x,y), оно становится уравнением в полных дифференциалах. Определение. Функция g(x,y) называется интегрирующим множителем дифференциального уравнения M(x,y)dx+N(x,y)dy=0, Если после умножения его на эту функцию оно становится уравнением в полных дифференциалах. Данный способ решения дифференциального уравнения называется методом интегрирующего множителя. Найдем условие, которому должен подчиняться интегрирующий множитель g(x,y). Из предложения, что уравнение M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0 Становится уравнением в полных дифференциалах следует выполнение условия Разверернув левую и правую части этого тождества заключаем, что функция g(x,y) должна являться решением уравнения В общем случае решение данного уравнения вызывает затруднения. Отметим два случая, когда его решение становится проще. Случай первый. Пусть Тогда интегрирующий множитель можно искать в виде функции зависящей только от x. Действительно, пусть g=g(x). Тогда в виду ; получаем, что искомая функция g(x) является решением дифференциального уравнения интегрируя которое, находим Второй слуяай относится к аналогичной ситуации, когда Тогда интегрирующий множитель ищется в виде функции только от y, т.е. g=g(y). Аналогично предыдущему, не трудно видеть, что функция g(y) является решением уравнения и представляется в виде Пример 3. Дано уравнение (y2-3xy-2x2)dx+(xy-x2)dy=0. Из M(x,y)=y2-3xy-2x2, N(x,y)=xy-x2, , , т.е. уравнение не является в полных дифференциалах. Однако из соотношения вытекает, что можно найти такой интегрирующий множитель g=g(x), после умножения на который исходное уравнение становится уравнением в полных дифференциалах. Указанный множитель находим из уравнения интегрируя которое получаем , или g=xc. Так как в качестве множителя достаточно взять одну из функций, то положим c=1 и, тогда, g=x. Умножая исходное уравнение на множитель g=x, получаем (xy2-3x2y-2x3)dx+(x2y-x3)dy=0, являющееся уже уравнением в полных дифференциалах. Интегрируя его, находим , затем из U/y=x2y-x3+h/(x) и U/y=N(x,y)=x2y-x3 получаем x2y-x3+h/=x2y-x3, т.е. следовательно, h=c=const. Таким образом, общее решение имеет вид Пример 4. Требуется решить уравнение (2xy2-y)dx+(y2+x+y)dy=0. Из M(x,y)=2xy2-y, N(x,y)=y2+x+y, Однако из соотношения вытекает, что для исходного дифференциального уравнения существует интегрирующий множитель g=g(y), с помощью которого уравнение становится уравнением в полных дифференциалах. Интегрирующий множитель находится из уравнения Интегрируя его, получаем Умножая исходное уравнение на множитель Это уравнение является уже уравнением в полных дифференциалах. Решаем его затем из получаем Интегрируя последнее уравнение, имеем Таким образом, общий интеграл исходного уравнения имеет вид 9. Дифференциальные уравнения второго порядка. Обыкновенное дифференциальное уравнение второго порядка имеет следующий общий вид F(x,y,y/,y//)=0 или Наше знакомство с дифференциальными уравнениями второго порядка будет ограничено рассмотрением линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Определение. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y//+py/+qy=h(x), где p и q – числа, h(x) – некоторая функция от x. Если в этом уравнении , то оно называется однородным линейным дифференциальным уравнением второго порядка. Рассмотрим решение однородного уравнения Этому явлению может быть поставлено в соответствие квадратное уравнение вида Называемое характеристическим. Его корни Возможны следующие три случая для вида корней этого уравнения: 1) корни уравнения – действительные и различные; 2) корни – действительные и равные; 3) корни уравнения – комплексно-сопряженные. Для каждого из этих случаев однородное дифференциальное уравнение имеет свой вид общего интеграла. Случай 1. Дискриминант характеристического уравнения положителен, т.е. p2 -4q>0. Тогда оба корня действительные и различные. В этом случае общее решение однородного уравнения имеет вид где c1, c2 – произвольные постоянные. Действительно, если , то . Подставляя выражения для y,y/ и y// в уравнение получим . Случай 2. Дискриминант характеристического квадратного уравнения равен нулю, т.е p2-4q=0. Тогда оба корня В этом случае общее решение однородного уравнения имеет вид Случай 3. Дискриминант характеристического квадратного уравнения отрицателен, т.е. p2-4q<0. Тогда говорят, что квадратное уравнение не имеет действительных корней (или что оба корня являются комплексно-сопряженными). В этом случае, обозначая , общее решение однородного уравнения дается в виде Рассмотрим теперь решение неоднородного уравнения y//+py/+g(y)\h(x), где h(x) – некоторая функция от x. Пусть в этом уравнении q=0, тогда, используя подстановку y/=z, y //=z/, приходим к решению линейного дифференциального уравнения первого порядка z/+pz=h(x). Страницы: 1, 2 |
|
© 2010 |
|
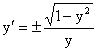 или
или 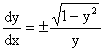 .
.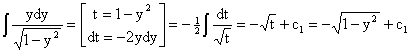
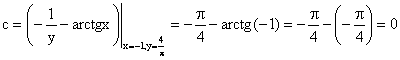
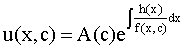
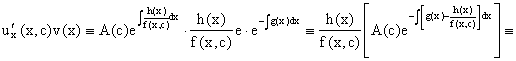
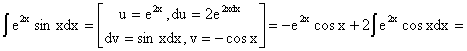
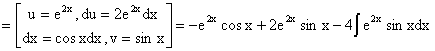
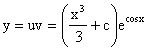 .
.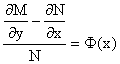 .
.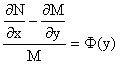 .
.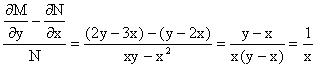
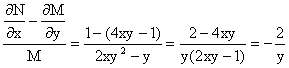 ,
,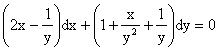 .
.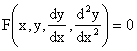 .
.