|
РУБРИКИ |
Курсовая: Определители и системы линейных уравнений |
РЕКОМЕНДУЕМ |
||
|
Курсовая: Определители и системы линейных уравненийКурсовая: Определители и системы линейных уравнений1. Определители второго и третьего порядков и их свойства 1.1. Понятие матрицы и определителя второго порядка содержащую произвольное число т строк и произвольное число и столбцов, называют матрицей. Для обозначения матрицы используют либо сдвоенные вертикальные черточки, либо круглые скобки. Например: 28 20 18 28 20 18 -6 11 2 -6 11 2 Если число строк матрицы совпадает с числом ее столбцов, то матрица называется квадратной. Числа, входящие в состав матрицы, называют ее элементами. Рассмотрим квадратную матрицу, состоящую из четырех элементов: (3.1) Определителем второго порядка, соответствующим матрице (3.1), называется число, равное - и обозначаемое символом Итак, по определению Элементы, составляющие матрицу данного определителя, обычно называют элементами этого определителя. Справедливо следующее утверждение: для того чтобы определитель второго порядка был равен нулю, необходимо и достаточно, чтобы элементы его строк (или соответственно его столбцов) были пропорциональны. Для доказательства этого утверждения достаточно заметить, что каждая из пропорций = и = эквивалентна равенству = , а последнее равенство в силу (3.2) эквивалентно обращению в нуль определителя. 1.2. Система двух линейных уравнений с двумя неизвестными Покажем, как применяются определители второго порядка для исследования и отыскания решений системы двух линейных уравнений с двумя неизвестными (коэффициенты , и свободные члены считаются при этом заданными). Напомним, что пара чисел , решением системы (3.3), если подстановка этих чисел на место и обращает оба уравнения (3.3) в тождества. Умножая первое уравнение системы (3.3) на - , а второе — на - затем складывая полученные при этом равенства, получим ( Аналогично путем умножения уравнений (3.3) на - ( Введем следующие обозначения: С помощью этих обозначений и выражения для определителя второго порядка уравнения (3.4) и (3.5) могут быть переписаны в виде: Определитель составленный из коэффициентов при неизвестных системы (3.3), принято называть определителем этой системы. Заметим, что определители и определителя системы посредством замены его первого или соответственно второго столбца свободными членами. Могут представиться два случая: 1) определитель системы отличен от нуля; 2) этот определитель равен нулю. Рассмотрим сначала случай 0. Из уравнений (3.7) мы сразу же получаем формулы для неизвестных, называемые формулами Крамера: Полученные формулы Крамера (3.8) дают решение системы (3.7) и потому доказывают единственность решения исходной системы (3.3). В самом деле, система (3.7) является следствием системы (3.3), поэтому всякое решение системы (3.3) (в случае, если оно существует!) должно являться решением и системы (3.7). Итак, пока доказано, что если у исходной системы (3.3) существует при 0 решение, то это решение однозначно определяется формулами Крамера (3.8). Легко убедиться и в существовании решения, т. е. в том. что при 0 два числа . определяемые формулами Крамера (3.8). будучи поставлены на место неизвестных в уравнения (3.3), обращают эти уравнения в тождества. (Предоставляем читателю самому расписать выражения для определителей , , и убедиться в справедливости указанных тождеств.) Мы приходим к следующему выводу: если определитель системы (3.3) отличен от нуля, то существует, и притом единственное решение этой системы, определяемое формулами Крамера (3.8). Рассмотрим теперь случай, когда определитель системы равен нулю. Могут представиться два подслучая: а) хотя бы один из определителей или нуля; б) оба определителя и определитель один из двух определителей и другой из указанных двух определителей равен нулю. В самом деле, пусть, например = 0, т.е. = и = . Тогда из этих пропорций получим, что / / = 0). В подслучае а) оказывается невозможным хотя бы одно из равенств (3.7), т. е. система (3.7) не имеет решений, а поэтому не имеет решений и исходная система (3.3) (следствием которой является система (3.7)). В подслучае б) исходная система (3.3) имеет бесчисленное множество решений. В самом деле, из равенств = = 0 и из утверждения в конце разд. 1.1 заключаем, что второе уравнение системы (3.3) является следствием первого и его можно отбросить. Но одно уравнение с двумя неизвестными имеет бесконечно много решений (хотя бы один из коэффициентов , или нуля, и стоящее при нем неизвестное может быть определено из уравнения (3.9) через произвольно заданное значение другого неизвестного). Таким образом, если определитель системы (3.3) равен нулю, то система (3.3) либо вовсе не имеет решений (в случае, если хотя бы один из определителей или нуля), либо имеет бесчисленное множество решений (в случае, когда = случае два уравнения (3.3) можно заменить одним и при решении его одно неизвестное задавать произвольно. Замечание. В случае, когда свободные члены и линейная система (3.3) называется однородной. Отметим, что однородная система всегда имеет так называемое тривиальное решение: = 0, числа обращают оба однородных уравнения в тождества). Если определитель однородной системы отличен от нуля, то эта система имеет только тривиальное решение. Если же = 0, то однородная система имеет бесчисленное множество решений (поскольку для однородной системы возможность отсутствия решений исключена). Таким образом, однородная система имеет нетривиальное решение в том и только в том случае, когда определитель ее равен нулю. 1.3. Определители третьего порядка Рассмотрим квадратную матрицу, состоящую из девяти элементов
Определителем третьего порядка, соответствующим матрице (3.10), называется число, равное: и обозначаемое символом Итак, по определению
Как и в случае определителя второго порядка, элементы матрицы (3.10) будем называть элементами самого определителя. Кроме того, договоримся называть диагональ, образованную элементами , , главной, а диагональ, образованную элементами , — побочной. Для запоминания конструкции слагаемых, входящих в выражение для определителя (3.11), укажем следующее правило, не требующее большого напряжения внимания и памяти. Для этого к матрице, из которой составлен определитель, допишем справа еще раз первый, а затем второй столбец. В полученной при этом матрице сплошной чертой соединены три тройки членов, получаемые параллельным переносом главной диагонали и отвечающие трем слагаемым, входящим в выражение (3.11) со знаком «плюс»; пунктирной же чертой соединены три другие тройки членов, получаемые параллельным переносом побочной диагонали и отвечающие трем слагаемым, входящим в выражение (3.11) со знаком «минус». 1.4. Свойства определителей Свойство 1. Величина определителя не изменится, если строки и столбцы этого определителя поменять ролями, т.е.
Для доказательства этого свойства достаточно расписать определители, стоящие в левой и правой частях (3.13), по указанному в разд. 1.3 правилу и убедиться в равенстве полученных при этом членов. Свойство 1 устанавливает полную равноправность строк и столбцов. Поэтому все дальнейшие свойства определителя можно формулировать и для строк, и для столбцов, а доказывать — или только для строк, или только для столбцов. Свойство 2. Перестановка двух строк (или двух столбцов) определителя равносильна умножению его на число -1. Доказательство также получается из правила, указанного в предыдущем разделе. Свойство 3. Если определитель имеет две одинаковые строки (или два одинаковых столбца), то он равен нулю. Действительно, при перестановке двух одинаковых строк, с одной стороны, определитель не изменится, а с другой стороны, в силу свойства 2 он изменит знак на противоположный. Таким образом, = - = 0 или Свойство 4. Умножение всех элементов некоторой строки (или некоторого столбца) определителя на число равносильно умножению определителя на это число . Иными словами, общий множитель всех элементов некоторой строки (или некоторого столбца) определителя можно выносить за знак этого определителя. |
|
© 2010 |
|
 Прямоугольную таблицу из чисел,
Прямоугольную таблицу из чисел,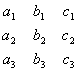
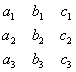
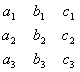 =
= 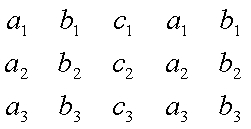
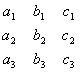 =
=