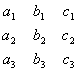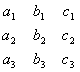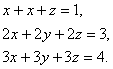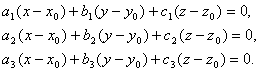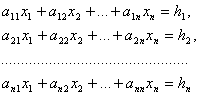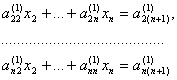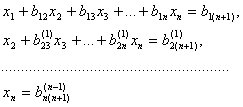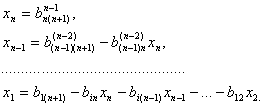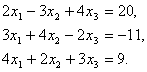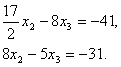|
РУБРИКИ |
Курсовая: Определители и системы линейных уравнений |
РЕКОМЕНДУЕМ |
||
|
Курсовая: Определители и системы линейных уравнений(3.19) соответственно на алгебраические дополнения , , элементов первого столбца определителя системы, и после этого сложим полученные при этом уравнения. В результате получим: (
= Учитывая, что сумма произведений элементов данного столбца определителя на соответствующие алгебраические дополнения элементов этого (другого) столбца равна определителю (нулю) (см. свойство 9), получим:
Кроме того, посредством разложения определителя по элементам первого столбца получается формула: С помощью формул (3.21) и (3.22) равенство (3.20) перепишется в следующем (не содержащем неизвестных и Совершенно аналогично выводятся из системы (3.19) равенства
Таким образом, мы установили, что система уравнений является следствием исходной системы (3.19). В дальнейшем мы отдельно рассмотрим два случая: 1) когда определитель системы 2) когда этот определитель равен нулю.
Итак, пусть 0. Тогда из системы (3.23) мы сразу получаем формулы для неизвестных, называемые формулами Крамера: Полученные нами формулы Крамера дают решение системы (3.23) и потому доказывают единственность решения исходной системы (3.19), ибо система (3.23) является следствием системы (3.19), и всякое решение системы (3.19) обязано быть решением и системы (3.23). Итак, мы доказали, что если у исходной системы (3.19) существует при 0 решение, то это решение однозначно определяется формулами Крамера (3.24). Чтобы доказать, что решение в самом деле существует, мы должны подставить в исходную систему (3.19) на место х, у и z их значения, определяемые формулами Крамера (3.24), и убедиться в том, что все три уравнения (3.19) обращаются при этом в тождества. Убедимся, например, что первое уравнение (3.19) обращается в тождество при подстановке значений х, у и z, определяемых формулами Крамера (3.24). Учитывая, что получим, подставив в левую часть первого из уравнений (2.19) значения , , определяемые формулами Крамера: = . Группируя внутри фигурной скобки члены относительно A,, А2 и Л3, получим, что: В силу свойства 9 в последнем равенстве обе квадратные скобки равны нулю, а круглая скобка равна определителю . Таким образом, мы получим + + , и обращение в тождество первого уравнения системы (3.19) установлено. Аналогично устанавливается обращение в тождество второго и третьего уравнений (3.19). Мы приходим к следующему выводу: если определитель системы (3.19) отличен от нуля, то существует, и притом единственное, решение этой системы, определяемое формулами Крамера (3.24). 2.2. Однородная система двух линейных уравнений с тремя неизвестными
В этом и в разделе мы разовьем аппарат, необходимый для рассмотрения неоднородной системы (3.19) с определителем, равным нулю. Сначала рассмотрим однородную систему двух линейных уравнений с тремя неизвестными: Если все три определителя второго порядка, которые можно составить из матрицы
равны нулю, то в силу утверждения из разд. 1.1 коэффициенты первого из уравнений (3.25) пропорциональны соответствующим коэффициентам второго из этих уравнений. Стало быть, в этом случае второе уравнение (3.25) является следствием первого, и его можно отбросить. Но одно уравнение с тремя неизвестными + + имеет бесчисленное множество решений (двум неизвестным можно предписывать произвольные значения, а третье неизвестное определять из уравнения). Рассмотрим теперь систему (3.25) для случая, когда хотя бы один из определителей второго порядка, составленных из матрицы (3.26), отличен от нуля. Не ограничивая общности, будем считать, что отличен от нуля определитель
Тогда мы можем переписать систему (3.25) в виде и утверждать, что для каждого z существует единственное решение этой системы, определяемое формулами Крамера (см. разд. 1.2, формулы (3.8)):
Далее удобно использовать алгебраические дополнения , элементов третьей строки определителя: В силу результатов разд. 1.5 о связи алгебраических дополнений и миноров можно записать
Основываясь на (3.29), мы можем переписать формулы (3.28) в виде
Для того чтобы получить решение в виде, симметричном относительно всех неизвестных х, у, и z, положим (отметим, что в силу (3.27) определитель отличен от нуля). Поскольку z может принимать любые значения, то и новая переменная t может принимать любые значения.
Мы приходим к выводу, что в случае, когда определитель (3.27) отличен от нуля, однородная система (3.25) имеет бесчисленное множество решений, определяемых формулами в которых t принимает какие угодно значения, а алгебраические дополнения , определяются формулами (3.29). 2.3. Однородная система трех линейных уравнений с тремя неизвестными Рассмотрим теперь однородную систему трех уравнений с тремя неизвестными:
Очевидно, что эта система всегда имеет так называемое тривиальное решение: х = 0, у = 0, z = 0. В случае, когда определитель системы , это тривиальное решение является единственным (в силу разд. 2.1). Докажем, что в случае, когда определитель равен нулю, однородная система (3.32) имеет бесчисленное множество решений. Если все определители второго порядка, которые можно составить из матрицы равны нулю, то в силу утверждения из разд. 1.1 соответствующие коэффициенты всех трех уравнений (3.32) пропорциональны. Но тогда второе и третье уравнения (3.32) являются следствиями первого и могут быть отброшены, а одно уравнение + + отмечалось в разд. 2.2, имеет бесчисленное множество решений. Остается рассмотреть случай, когда хотя бы один минор матрицы (3.33) отличен от нуля. Так как порядок следования уравнений и неизвестных находится в нашем распоряжении, то, не ограничивая общности, мы можем считать, что отличен от нуля определитель (3.27). Но тогда, как установлено в разд. 2.2, система первых двух уравнений (3.32) имеет бесчисленное множество решений, определяемых формулами (3.31) (при любом t). Остается доказать, что х, у, z, определяемые формулами (3.31) (при любом t, обращают в тождество и третье уравнение (3.32). Подставляя в левую часть третьего уравнения (3.32) х, у и z, определяемые формулами (3.31), получим Мы воспользовались тем, что в силу свойства 9 выражение в круглых скобках равно определителю системы (3.32). Но определитель по условию равен нулю, и поэтому при любом t мы получим + + Итак, доказано, что однородная система (3.32) с определителем А. равным нулю, имеет бесчисленное множество решений. Если отличен от нуля минор (3.27), то эти решения определяются формулами (3.31) при произвольно взятом t. Полученный результат можно сформулировать еще и так: однородная система (3.32) имеет нетривиальное решение в том и только в том случае, когда определитель ее равен нулю. 2.4. Неоднородная система трех линейных уравнений с тремя неизвестными с определителем, равным нулю. Теперь мы располагаем аппаратом для рассмотрения неоднородной системы (3.19) с определителем , равным нулю. Могут представиться два случая: а) хотя бы один из определителей , - отличен от нуля; б) все три определителя , равны нулю. В случае а) оказывается невозможным хотя бы одно из равенств (3.23), т. е. система (3.23) не имеет решений, а поэтому не имеет решений и исходная система (3.19) (следствием которой является система (3.23)). Переходим к рассмотрению случая б), когда все четыре определителя , и с примера, показывающего, что и в этом случае система может не иметь ни одного решения. Рассмотрим систему: Ясно, что эта система не имеет решений. В самом деле, если бы решение , существовало, то из первых двух уравнений мы получили бы , умножая первое равенство на 2, получили бы, что 2 = 3. Далее, очевидно, что все четыре определителя , и Действительно, определитель системы имеет три одинаковых столбца, определители , получаются путем замены одного из этих столбцов свободными членами и, стало быть, имеют по два одинаковых столбца. В силу свойства 3 все эти определители равны нулю. Докажем теперь, что если система (3.19) с определителем , равным нулю, имеет хотя бы одно решение, то она имеет бесчисленное множество различных решений. Предположим, что указанная система имеет решение , . Тогда справедливы тождества
Вычитая почленно из уравнений (3.19) тождества (3.34), получим систему уравнений
эквивалентную системе (3.19). Но система (3.35) является однородной системой трех линейных уравнений относительно трех неизвестных , с определителем , равным нулю. Согласно разд. 2.3 последняя система (а стало быть, и система (3.19)) имеет бесчисленное множество решений. Например, в случае, когда отличен от нуля минор (3.27), мы с помощью формул (3.31) получим следующее бесконечное множество решений системы (3.19): (t принимает любые значения). Сформулированное утверждение доказано, и мы можем сделать следующее заключение: если = = 0, то неоднородная система уравнений (3.19) либо совсем не имеет решений, либо имеет их бесконечное множество. 3. Понятие об определителях любого порядка и о линейных системах с любым числом неизвестных Установленное нами свойство разложения определителя третьего порядка до элементам любой (например, первой) строки может быть положено в основу последовательного введения по индукции определителя четвертого, пятого и всех последующих порядков. Предположим, что нами уже введено понятие определителя порядка (n-1), и рассмотрим произвольную квадратную матрицу состоящую из элементов Назовем минором любого элемента матрицы (3.36) уже введенный нами определитель порядка (n-1), отвечающий матрице (3.36), у которой удалены i-я строка и j-й столбец. Договоримся обозначать минор элемента символом Например, минор любого элемента первой строки матрицы (3.36) является следующим определителем порядка (n-1): Назовем определителем порядка n, отвечающим матрице (3.36), число , равное сумме
и обозначаемое символом
Заметим, что при n = 3 разложение (3.37) совпадает с разложением (3.16) определителя третьего порядка по первой строке. Рассмотрим теперь неоднородную систему n уравнений с n неизвестными:
Определитель порядка n, составленный из коэффициентов при неизвестных системы (3.39) и совпадающий с определителем из равенства (3.38), называется определителем этой системы При любом j, равном 1, 2, ..., n, обозначим символом определитель порядка n, полученный из определителя системы путем замены его j-го столбца столбцом свободных членов , . В полной аналогии со случаем n = 3 оказывается справедлив следующий результат: если определитель неоднородной системы (3.39) отличен от нуля, то эта система имеет единственное решение, определяемое формулами Крамера: Далее можно доказать, что если определитель системы равен нулю, а хотя бы один из определителей , отличен от нуля, то система (3.39) не имеет решений. В случае же, если n > 2 и все определители , , ..., система (3.39) может также не иметь решений, но если она имеет хотя бы одно решение, то она имеет их бесчисленное множество. 4. Отыскание решения линейной системы методом Гаусса Рассмотрим неоднородную систему (3.39), в которой мы теперь для сокращения записи переобозначим свободные члены , , используя для них обозначение при i = 1, 2 ..., n. Изложим один из самых простых методов решения этой системы, заключающийся в последовательном исключении неизвестных и называемый методом Гаусса. Выберем из коэффициентов при неизвестных коэффициент, отличный от нуля, и назовем его ведущим. Не ограничивая общности, будем считать, что таким коэффициентом является (иначе мы могли бы поменять порядок следования неизвестных и уравнений).
Поделив все члены первою уравнения (3.39) на , получим первое приведенное уравнение в котором Напомним, что Для исключения неизвестного умноженное на В результате получим для любого i = 2, 3, ..., n уравнение в котором
коэффициенты которой определяются по формулам (3.41). В системе (3.42) находим отличный от нуля ведущий коэффициент. Пусть это будет . Тогда, поделив первое уравнение (3.42) на этот коэффициент, мы получим второе приведенное уравнение и, исключив с помощью этого уравнения по описанной выше схеме неизвестное , придем ко второй укороченной системе, не содержащей и схеме, называемой прямым ходом метода Гаусса, мы либо завершим ее реализацию, дойдя до линейного уравнения, содержащего только одно неизвестное, либо не сможем завершить ее реализацию (вследствие того, что исходная система (3.39) не имеет решений). В случае, если исходная система (3.39) имеет решения, мы получим цепочку приведенных уравнений из которой обратным xодом метода Гаусса последовательно находятся неизвестные
Подчеркнем, что все операции при обратном ходе метода Гаусса (1.43) выполняются без деления, В качестве примера рассмотрим неоднородную систему трех уравнений с тремя неизвестными
Конечно, можно убедиться в том, что определитель системы (3.44) отличен от нуля, и найти и Крамера, но мы применим метод Гаусса. Поделив первое уравнение системы (3.44) на 2, получим первое приведенное уравнение:
уравнения системы (3.44) приведенное уравнение (3.45), умноженное на 3, и вычитая из третьего уравнения системы (3.44) приведенное уравнение (3.45), умноженное на 4, мы получим укороченную систему двух уравнений с двумя неизвестными:
Поделив первое уравнение (3.46) на
Вычитая из второго уравнения (3.46) приведенное уравнение (3.47), умноженное на 8, получим уравнение: которое после сокращения на Подставляя это значение во второе приведенное уравнение (3.47), получим, что = -2. Наконец, подставляя найденные значения = -2 и приведенное уравнение (3.45), получим, что = 1. ЛИТЕРАТУРА 1. Ильин В.А., Куркина А.В. – «Высшая математика», М.:ТК Велби, изд-во Проспект, 2004г. – 600с. |
|
© 2010 |
|
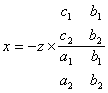 ,
, 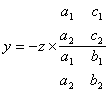 .
.