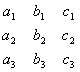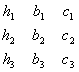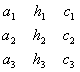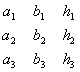|
РУБРИКИ |
Курсовая: Определители и системы линейных уравнений |
РЕКОМЕНДУЕМ |
||
|
Курсовая: Определители и системы линейных уравненийНапример, Для доказательства этого свойства достаточно заметить, что определитель выражается в виде суммы (3.12), каждый член которой содержит один и только один, элемент из каждой строки и один и только один элемент из каждого столбца. Свойство 5. Если все элементы некоторой строки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю. Это свойство вытекает из предыдущего (при Свойство 6. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. В самом деле, в силу свойства 4 множитель пропорциональности можно вынести за знак определителя, после чего остается определитель с двумя одинаковыми строками, равный нулю согласно свойству 3. Свойство 7. Если каждый элемент п-й строки (или п-го столбца) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, первый из которых имеет в п-й строке (или в п-м столбце) первые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах), а второй определитель имеет в п-й строке (в п-м столбце) вторые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах). Например, Для доказательства этого свойства снова достаточно заметить, что определитель выражается в виде суммы слагаемых, каждое из которых содержит один и только один элемент из каждой строки и один и только один элемент из каждого столбца. Свойство 8. Если к элементам некоторой строки (или некоторого столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный множитель , то величина определителя не изменится. Действительно, полученный в результате указанного прибавления определитель можно (в силу свойства 7) разбить на сумму двух определителей, первый из которых совпадает с исходным, а второй равен нулю вследствие пропорциональности элементов двух строк (или столбцов) и свойства 6. 1.5. Алгебраические дополнения и миноры Соберем в выражении (3.12) для определителя члены, содержащие какой-нибудь один элемент этого определителя, и вынесем указанный элемент за скобки; величина, остающаяся при этом в скобках, называется алгебраическим дополнением указанного элемента. Алгебраическое дополнение данного элемента мы будем обозначать прописной латинской буквой того же наименования, что и данный элемент, и снабжать тем же номером, который имеет данный элемент. Например, алгебраическое дополнение элемента обозначать через алгебраическое дополнение элемента — через Непосредственно из выражения для определителя (3.12) и из того, что каждое слагаемое в правой части (3.12) содержит один и только один элемент из каждой строки (из каждого столбца), вытекают следующие равенства:
Эти равенства выражают следующее свойство определителя: определитель равен сумме произведений элементов какой-либо строки (какого-либо столбца) на соответствующие алгебраические дополнения элементов этой строки (этого столбца). Равенства (3.14) принято называть разложением определителя по элементам соответственно первой, второй или третьей строки, а равенства (3.15) — разложением определителя по элементам соответственно первого, второго или третьего столбца. Введем теперь важное понятие минора данного элемента определителя Минором данного элемента определителя n-го порядка (в нашем случае n = 3) называется определитель (n-1)-го порядка, получаемый из данного определителя путем вычеркивания той строки и того столбца, на пересечении которых стоит данный элемент. Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со таком «плюс», если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, есть число четное, и со знаком «минус» — в противном случае. Таким образом, соответствующие алгебраическое дополнение и минор могут отличаться только знаком. Следующая таблица дает наглядное представление о том, каким знаком связаны соответствующие алгебраическое дополнение и минор: Установленное правило позволяет в формулах (3.14) и (3.15) разложения определителя по элементам строк и столбцов всюду вместо алгебраических дополнений писать соответствующие миноры (с нужным знаком). Так, например, первая из формул (3.14), дающая разложение определителя по элементам первой строки, принимает вид
В заключение установим следующее фундаментальное свойство определителя. Свойство 9. Сумма произведений элементов какого-либо столбца определителя на соответствующие алгебраические дополнения элементов этого {другого) столбца равна величине этого определителя (равна нулю). Конечно, аналогичное свойство справедливо и в применении к строкам определителя. Случай, когда алгебраические дополнения и элементы отвечают одному и тому же столбцу, уже рассмотрен выше. Остается доказать, что сумма произведений элементов какого-либо столбца на соответствующие алгебраические дополнения элементов другого столбца равна нулю. Докажем, например, что сумма произведений элементов первого или второго столбца на соответствующие алгебраические дополнения элементов третьего столбца равна нулю. Будем исходить из третьей формулы (3.15), дающей разложение определителя по элементам третьего столбца:
Так как алгебраические дополнения , элементов третьего столбца не зависят от самих элементов , этого столбца, то в равенстве (3.17) числа , можно заменить произвольными числами , , сохраняя при этом в левой части (3.17) первые два столбца определителя, а в правой части — величины , алгебраических дополнений. Таким образом, при любых
Беря теперь в равенстве (3.18) в качестве , сначала элементы и а затем элементы и учитывая, что определитель с двумя совпадающими столбцами в силу свойства 3 равен нулю, мы придем к следующим равенствам: Тем самым доказано, что сумма произведений элементов первого или второго столбца на соответствующие алгебраические дополнения элементов третьего столбца равна нулю: Аналогично доказываются равенства: и соответствующие равенства, относящиеся не к столбцам, а к строкам: 2. Системы линейных уравнений с тремя неизвестными 2.1. Системы трех линейных уравнений с тремя неизвестными с определителем, отличным от нуля. В качестве приложения изложенной выше теории рассмотрим систему трех линейных уравнений с тремя неизвестными:
(коэффициенты , , , , члены , заданными). Тройка чисел , называется решением системы (3.19), если подстановка этих чисел на место , в систему (3.19) обращает все три уравнения (3.19) в тождества. Фундаментальную роль в дальнейшем будут играть следующие четыре определителя: Определитель принято называть определителем системы (3.19) (он составлен из коэффициентов при неизвестных). Определители , получаются из определителя системы посредством замены свободными членами элементов соответственно первого, второго и третьего столбцов. Для исключения из системы (3.19) неизвестных и |
|
© 2010 |
|
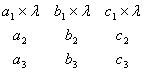 =
= 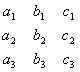
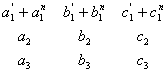 =
= 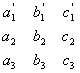 +
+ 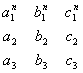
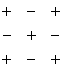
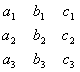 =
= 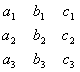 =
= 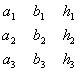 =
=