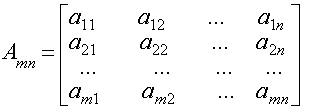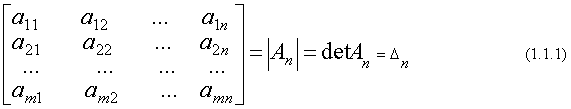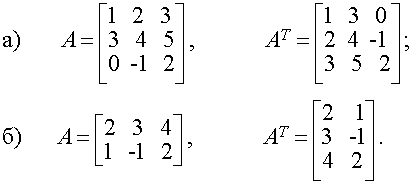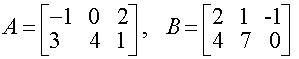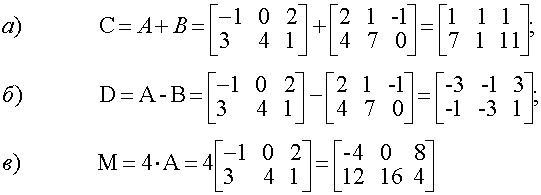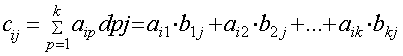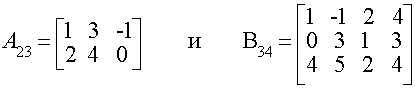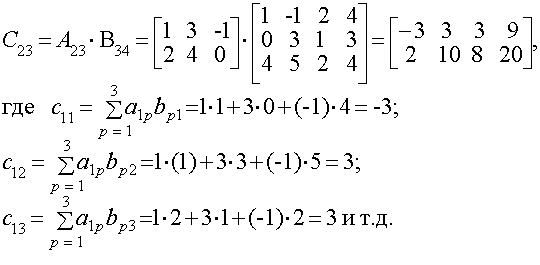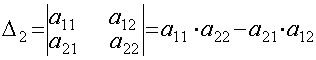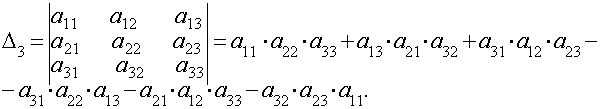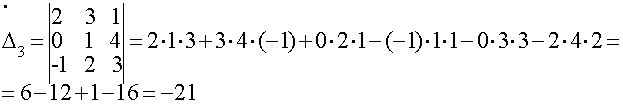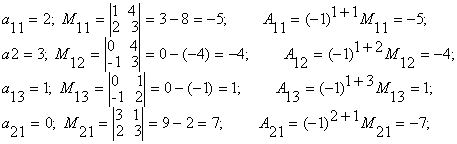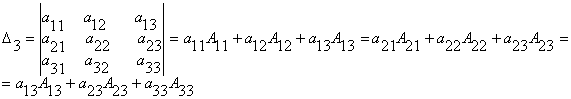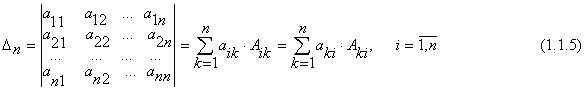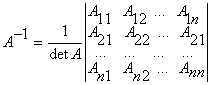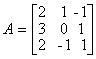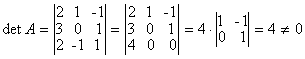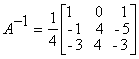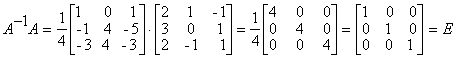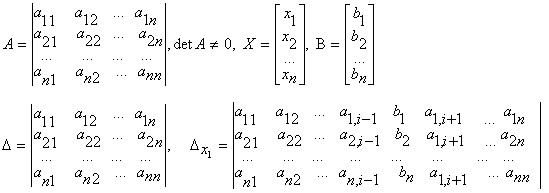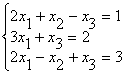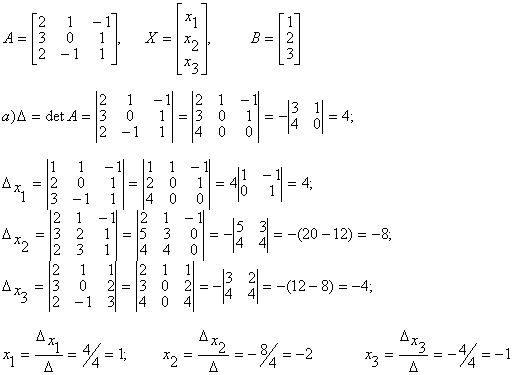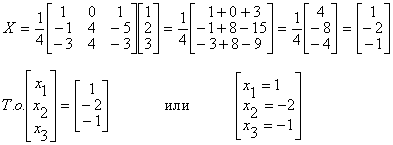Методические указания: Методические указания и рабочая программа по курсу «Высшая математика»

Методические указания: Методические указания и рабочая программа по курсу «Высшая математика»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

Государственный аэрокосмический университет им. Н. Е. Жуковского «ХАИ»

Международная Ассоциация выпускников ХАИ

Факультет заочного образования

Методические указания и рабочая программа по курсу

«ВЫСШАЯ МАТЕМАТИКА»

Для студентов заочной формы обучения

Харьков ХАИ 1998

Утверждено методической

комиссией факультета № 9

(Протокол №'3 от 11 декабря 1997г.)

СОСТАВИТЕЛИ :

Брысина Ирина Викторовна Головченко Александр Васильевич Кошевой Георгий

Иванович Кощавец Петр Тихонович Крашаница Юрий Александрович Николаев Алексей

Георгиевич Проценко Владимир Сидорович Рвачев Владимир Алексеевич Томилова

Евгения Павловна Ушакова Елена Григорьевна Хоменко Владимир Васильевич

Содержание

тема НАИМЕНОВАНИЕ ТЕМЫ

Стр.

Введение. ............. 5

Программа курса по высшей математике 8

раздел 1. Матрицы и определители. Векторная алгебра.

Аналитическая геометрия.

Элементы линейной алгебры. . ... 13

Тема 1.1. 'Матрицы и определители. Системы

линейных алгебраических уравнений

(СЛАУ) ................ 13

Тема 1.2. Векторная алгебра .... ....24

Тема 1.3. Прямая и плоскость. ........ 34

Тема 1.4. Преобразование координат на плоско­сти.

Элементарная теория линий второ­го порядка. 41

Тема 1.5. Некоторые сведения о линейных

векторных пространствах. Собственные

числа и собственные векторы. .... 44

Тема 1.6. Квадратичные формы. Приведение

каноническому виду уравнений линии и

поверхности второго порядка. .... 49

Дополнение 1.1. Образец выполнения и оформления

контрольной работы N 1. « Векторная алгебра и

аналитическая геометрия.

'Матрицы. Элементы линейной алгебры.» 53

раздел 2. Дифференциальное исчисление. .... 59

Тема 2.1. Введение в анализ. .......... 59

Тема 2.2. Производная и дифференциалы. .... 64

тема 2.3. Приложения производной. ....... 66

Тема 2.4. Комплексные числа. ......... 71

Дополнение 2.1. Образец выполнения и оформления

контрольной работы N 2 «Дифференци­альное

исчисление.». . . 72

раздел 3. Функции нескольких переменных.... 76

Тема 3.1. Частные производные. ........ 76

Тема 3.2. Экстремум функции. ......... 78

тема 3.3. Геометрические приложения функций

не­скольких переменных. ........ 80

раздел 4. Интегральное исчисление функции одной

переменной............. 82

Тема 4.1. Неопределенный интеграл. ...... 82

Тема 4.2. Определенный интеграл. ....... 91

Тема 4.3. Несобственный интеграл. ....... 97

раздел 5. Дифференциальные уравнения. ..... 102

Тема 5.1. Уравнения первого порядка. ..... 102

Тема 5.2. Уравнения высших порядков. . . .•. . 103

Тема 5.3. Системы дифференциальных уравнений.

105 Дополнение 5.1. Образец выполнения и оформления кон-

трольной работы

N 3. «Дифференциальное исчисление

функций нескольких переменных.

Интегральное исчисление функций

одной переменной. Дифференциальные

уравнения.» ............ 106

раздел б. Кратные интегралы. Элементы теории

векторного поля. .......... 112

Тема 6.1. Некоторые вспомогательные

определения. ............ 112

Тема 6.2. Двойной интеграл. .......... 112

Тема 6.3. Тройной интеграл. .......... 126

Тема 6.4. Криволинейные интегралы. ...... 132

Тема 6.5. Элементы векторного анализа. .... 137

раздел 7 Числовые и функциональные ряды. Ряды

Фурье . Интеграл Фурье....... 145

Тема 7.1. Числовые ряды. Ряды с положительными

Членами. Ряды с членами любого знака.

Знакочередующиеся ряды. .... 145

Тема 7.2. Функциональные ряды. Приложения рядов

к приближенным вычислениям. Приближенное

решение дифференциальных уравнений. ........... 148

Тема 7.3. Ряды Фурье. ............ 152

Тема 7.4. Интеграл Фурье. Преобразование Фурье.

155 Дополнение 7.1. Образен выполнения и оформления

контрольной работы N 4. «Кратные

интегралы. Ряды. Ряды Фурье.» . . . 157

ВВЕДЕНИЕ

Основной формой обучения студента-заочника является самостоя­тельная

систематическая работа над учебным материалом. Организуе­мые для студентов

лекции, практические занятия и консультации при­званы помочь им в

самостоятельной работе. Количество часов, отве­денных на аудиторную работу

составляет 25 процентов от общего чис­ла часов, отведенных на изучение курса.

Общий курс математики является фундаментом математического образования

инженера. Преподавание математики имеет целью выработ­ку у студентов умения

проводить анализ прикладных задач и овладе­ние основными математическими

методами исследования и решения та­ких задач.

В настоящем пособии приведена программа курса по высшей мате­матике с

указанием количества часов, отводимых на изучение темы, указано, в какой

последовательности надо изучать рекомендуемую ли­тературу, какие задачи

необходимо решить. Каждый раздел содержит ссылку на литературу, позволяющую

изучить основной теоретический материал, вопросы для самопроверки, номера

задач, которые рекомен­дуются к решению, краткие методические указания. После

изучения темы необходимо выполнить контрольную работу. Приведены образцы

оформления и выполнения контрольных заданий.

В пособии используется тройная нумерация формул, примеров и рисунков. Первая

цифра указывает номер раздела, вторая - номер те­мы, третья - порядковый

номер объекта на который производится ссылка.

Для изучения курса высшей математики студенту рекомендуется следующая

литература, применительно к которой и составлено настоя­щее пособие.

Список использованной и рекомендуемой литературы

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгеб­ры . -

М.:Наука,1985.

2. Беклемишева Л.А., Петрович А.Ю., Чубаров И. А. Сборник задач по аналитической

геометрии и линейной алгебре. -М.:Наука, 1987 .

3. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1972.

4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. -

М. : Наука,, 1980.

5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Крат­ные

интегралы. Ряды. Функции комплексного переменного. -М. : Нау­ка, 1981.

6. Будак В.М., Фомин С.В. Кратные интегралы и ряды. М., 1927.

7. Вища математика. Оснсвны означення, приклади і задачі. Навчальний

посібник. /Кулініч Г.Л., Максименко В.В. та ін./. В 2-ох кн.

-К.: Либідь, 1994.

8. Данко П.Е., Попов А. Г., Кожевникова Т.Е. Высшая математика в упражнениях

и задачах. В 2 ч. М., 1980.

9. Ильин В.А., Позняк Э.Г. Основы математического анализа. В 2 ч.

-М.: Наука, 1982.

10. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. -М. : Наука, 1982.

11. Каплан И.А. Практические занятия по высшей математике. Харьков: Изд-во

Харьк. Ун-та, 1965.

12. Краснов М.Л., Киселев А.И./ Макаренко Г.И. Векторный анализ. -М. : Наука,

1978.

13. Краснов М.Л., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновенным

дифференциальным уравнениям. -М.: Высшая школа, 1978.

14. Марон И.А. Дифференциальное и интегральное исчисление в приме­рах и

задачах. -М.: Наука, 1965.

15. Минорский В.Д. Сборник задач по высшей математике. -М.: Наука, 1987.

16. Мышкис А.Д. Лекции по высшей математике. -М. : Наука, 1973.

17. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2т. -М.:

Наука, 1968.

18. Проскуряков И.В. Сборник задач по линейной алгебре. -М. : Нау­ка, 1984.

19. Романовский П.И. Ряды Фурье. Теория поля. Аналитические и спе­циальные

функции. Преобразование Лапласа. -М. : Наука, 1980.

20. Сборник задач по математике. В 4ч. (Под редакцией Ефимова А.В.,

Демидовича Б.П.) -М.: Наука, 1981. Ч. 1-2.

21. Цубербиллер О.Н. Задачи и упражнения по аналитической геомет­рии. -М.:

Наука, 1966.

22. Эльсгольц Л.Э. Обыкновенные дифференциальные уравнения. -М. :

Наука, 1961.

Учебно-методические пособия кафедры высшей математики I.

І. Аналитическая геометрия и линейная алгебра

23. Найда Л.С., Рвачев В.А., Колодяжный В.М. Элементы линейной ал­гебры и

теории матриц. (Учебное пособие) ХАЙ, 1981.

24. Найда Л.С., Рвачев В.А., Колодяжный В.М. Линейные операторы и

квадратичные формы. (Учебное пособие) ХАЙ, 1982.

25. Робочий зошит з лінійної алгебри та аналітичної геометрії. ХАИ, 1997.

II. Математический анализ

26. Желдакова Л.В., Ушакова Е.Г. Приложение дифференциального ис­числения к

некоторым задачам физики и механики (учебное пособие) ХАИ, 1987,. .

27. Желдакова Л.В., Ушакова Е.Г. Дифференциальные уравнения. Харьков. ХАИ, 1991.

28. Забара С.И., Крашаница Ю.А. Элементы гармонического анализа (Учебное

пособие) ХАИ, 1981.

29. Искусство вычисления интегралов (Методические указания). Сост. Мещеряков

С.Ф. ХАИ, 1989,,

30. Кошевой Г.И. Николаев А.Г. Дифференциальное и интегральное ис­числение.

Примеры и задачи. Учебное пособие ХАИ, 1991, 87 с.

31. Кошевой Г.И., Старец Г.А. Числовые и функциональные ряды. Харьков, ХАИ,

1988.

32. Краснов В.П., Крашаниця Ю.А., Щербакова Ю.А. Задачі та вправи з курсу

вищої математики. ХАИ, 1994.

33. Лекции по высшей математике для студентов-заочников ХАИ. В Зч. Харьков,

ХАИ, 1998.

34. Мещеряков С.Ф. Исследование функций и построение графиков в полярной

системе координат и заданных параметрических ХАИ, 1991.

35. Мещеряков С.Ф. Построение графиков в полярной системе коорди­нат (учебное

пособие по высшей математике) ХАИ, 1975.

36. Робочий зошит з математичного аналізу. (Інтегрування функій однієї

змінної. Звичайні диференціальні рівняння. Кратні інтеграли.) Ч. 2.

ХАИ, 1998.

37. Скибин А. А. Интегральное исчисление и его приложения к задачам

геометрии, механики и физики. -Харьков, ХАИ, 1987.

38. Скибин А.А. Кратные интегралы и их приложения к задачам гео­метрии,

механики, физики. -Харьков, ХАИ, 1988.

39. Цымбалюк В. В. Применение криволинейных интегралов в задачах теории

поля. -Харьков, ХАИ, 1987.

40. Ярмолюк В.К., Лазарев А.И. Несобственные интегралы и интегра­лы,

зависящие от параметра. (Учебное пособие) ХАИ, 1983.

ПРОГРАММА КУРСА ПО ВЫСШЕЙ МАТЕМАТИКЕ

(70 часов)

1. Квадратные матрицы и определители второго и третьего порядков, их

свойства. Алгебраические дополнения и миноры. Определители n-го порядка.

Вычисление определителей. Системы линейных алгебраи­ческих уравнений 2-го, 3-

го и n-го порядков. Правило Крамера.

2. Матрицы, действия над ними. Обратная матрица. Матричный метод решения

линейных уравнений. Ранг матрицы и его вычисление. Тео­рема о базисном

миноре. Исследование системы линейных уравнений общего вида. Теорема

Кронекера-Капелли. Метод Гаусса решения систем линейных алгебраических

уравнений.

3. Определение вектора. Равенство векторов. Линейные операции над векторами и

их свойства. Линейная зависимость векторов. Базис. Разложение по базису.

Декартова система координат на плоскости и в пространстве. Деление отрезка в

данном отношении.

4. Скалярное произведение, его свойства. Длина вектора. Угол между двумя

векторами. Условия коллинеарности и перпендикулярности двух векторов.

5. Ориентация тройки векторов. Векторное произведение, его свойст­ва.

Векторное произведение в декартовой системе координат.

6. Смешанное произведение, его свойства. Вычисление смешанного произведения в

декартовой системе координат. Геометрический смысл определителя третьего

порядка. Компланарность трех векторов.

7. Прямая. Различные способы задания прямой на плоскости

(векторная и координатная формы) . Угол между двумя прямыми. Ус­ловия

параллельности и перпендикулярности прямых.

8. Векторная и координатная формы задания плоскости и прямой в и в

пространстве. Взаимное расположение прямой и плоскости.

9. Линии второго порядка, их канонические уравнения и свойства. Переход от

одной декартовой системы координат к другой на плос­кости.

10. Линейные пространства. Примеры. Линейная зависимость элемен­тов.

Евклидово пространство. Примеры. Неравенства Коши-Буняковского и

треугольника. Угол между векторами. Ортогональ­ность .

11. Понятие о линейном операторе и его матрице в данном базисе. Примеры

линейных операторов. Собственные векторы и собственные значения линейных

операторов.

12. Цилиндрические и конические поверхности. Поверхности вращения.

Канонические уравнения поверхностей второго порядка.

13. Квадратичные формы. Приведение квадратичных форм к ка­ноническому виду.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ (274 часа)

1. Введение в анализ (20 часов)

1.1. Числовые множества. Точные верхние и нижние грани числовых множеств.

Определение предела числовой последовательности и не­которые ее свойства.

Бесконечно малые и бесконечно большие по­следовательности. Арифметические

операции с последовательностя­ми. Существование предела монотонной

последовательности. Число е.

1.2. Теорема Больцано-Вейерштрасса и критерий Коши

(формулировка). Функции. График функции. Свойства пределов функций.

1.3. Замечательные пределы. Следствия из них. Бесконечно малые и 'бесконечно

большие функции. Сравнение бесконечно малых функций. Эквивалентные бесконечно

малые функции, их использование при оп­ределении пределов. Непрерывность

функций в точке. Классификация точек разрыва.

2. Дифференциальное исчисление функций одной переменной

(30 часов)

2.1. Локальные и глобальные свойства функции. Свойства функций, непрерывных

на отрезке (первая и вторая теоремы Вейерштрасса и ' теорема Коши).

Определение и свойства производной функции. Геометрический и механический

смысл производной.

2.2.. Производная сложной функции. Производная обратной функции.

Производные обратных тригонометрических функций. Функции, задан­ные

параметрически. Их дифференцирование. Таблицы производных простейших

элементарных функций. Дифференциал и его свойства.

2.3. Производные и дифференциалы высших порядков. Вторая производ­ная от

функции, заданной параметрически. Производная вектор-функции и ее

геометрический смысл. Возрастание (убывание) функ­ции в точке. Теоремы Ролля,

Лагранжа, Коши. Следствия из теоремы Лагранжа. Отыскание локальных и

глобальных" экстремумов функций. Раскрытие неопределенностей по правилу

Лопиталя.

3. Применение дифференциального исчисления для исследования функ­ций и

построения графиков (26 часов)

3.1. Формула и ряд Тейлора. Бином Ньютона, формулы Тейлора для элементарных

функций. Выпуклость функции. Точки перегиба. Асим­птоты функции. Построение

графиков функций.

3.2. Векторные функции скалярного аргумента и их дифферен­цирование.

Механический и геометрический смысл производной. Уравнения касательной прямой

и- нормальной плоскости.

3.3. Кривизна и радиус кривизны плоской кривой.

4. Элементы высшей алгебры (8 часов)

4.1. Комплексные числа, действия над ними. Изображение комплексных чисел на

плоскости. Геометрический смысл. Модуль и аргумент ком­плексного числа.

Алгебраическая и тригонометрическая формы ком­плексного числа. Формула

Эйлера.

4.2. Многочлены. Теорема Безу. Основная теорема алгебры. Разложе­ние

многочлена с действительными коэффициентами на линейные и квадратичные

множители. Разложение рациональных дробей на про­стейшие.

5. Дифференциальное исчисление функций нескольких

переменных (20 часов)

5.1. Область определения. Предел функции, непрерывность. Дифферен-цируемость

функции нескольких переменных, частные производные и полный дифференциал,

связь с частными производными. Производные от сложных функций. Инвариантность

формы полного дифференциала. Производные неявной функции.

5.2. Касательная плоскость и нормаль к поверхности. Геометрический смысл

полного дифференциала функции двух переменных.

5.3. Частные производные высших порядков. Теорема о независимости результата

дифференцирования от порядка дифференцирования. Дифференциалы высших

порядков.

5.4. Кривизна и кручение пространственной кривой. Формулы Френе.

5.5. Формула Тейлора для функции нескольких переменных. Экстремумы функций

нескольких переменных. Необходимые и достаточные условия экстремума. Условный

экстремум. Наибольшее и наименьшее значения функций в замкнутой области.

Метод множителей Лагранжа. Примеры применений при поиске оптимальных решений.

6. Интегральное исчисление функций одной переменной (40 часов)

6.1. Первообразная. Неопределенный интеграл. Основные свойства

не­определенного интеграла. Таблица интегралов. Интегрирование по частям и

методом замены переменной.

6.2. Интегрирование рациональных дробей, простейших

триго­нометрических выражений, линейных и дробно-линейных ирра-

циональностей. Квадратичные иррациональности.

6.3. Определенный интеграл, его свойства и методы вычислений. Не­собственные

интегралы. Приложения определенных интегралов в гео­метрии и механике.

7. Обыкновенные дифференциальные уравнения и системы (44 часа)

7.1. физические задачи, приводящие к дифференциальным уравнениям.

Основные понятия теории дифференциальных уравнений.

7.2. Дифференциальные уравнения первого порядка: с разделяющимися

переменными, однородные и приводящиеся к однородным, линейные уравнения,

уравнения в полных дифференциалах.

7.3. Задача Коши. Теорема существования и единственности решения задачи Коши.

Понятие особого решения дифференциального уравне­ния. Огибающая семейства

кривых.

7.4. Дифференциальные уравнения высших порядков. Задача Рюши. По­нятие о

краевых задачах для дифференциальных уравнений. Теорема существования и

единственности решения задачи Коши, Понятие об­щего и частного решений.

7.5. Уравнения допускающие понижение порядка. Линейные диф­ференциальные

уравнения высших порядков. Линейно-зависимые и ли­нейно-независимые системы

функций. Определитель Вронского, его свойства.

7.6. Линейные однородные дифференциальные уравнения с постоянными

коэффициентами, линейная независимость их решений, фундаменталь­ная система

решений.

7.7. Линейные неоднородные дифференциальные уравнения с по­стоянными

коэффициентами. Структура общего решения. Метод Лагранжа вариации

произвольных постоянных. Линейные неоднородные дифференциальные уравнения с

постоянными коэффициентами со спе­циальной правой частью.

7.8. Системы дифференциальных уравнений. Нормальные системы. Реше­ние

нормальной системы методом исключения. Задача Коши для нор­мальных систем.

7.9. Элементы теории устойчивости.

8. Криволинейные интегралы (6 часов)

8.1. Криволинейные интегралы первого рода, вычисление.

8.2. Криволинейные интегралы второго рода, вычисление, приложения.

Независимость криволинейного интеграла от формы пути интегриро­вания,

криволинейный интеграл от полного дифференциала, восста­новление функции по

полному дифференциалу.

9. Кратные интегралы (38 часов)

9.1 Двойной интеграл, условия существования и свойства. Вычисление двойного

интеграла в декартовой и полярной системах координат.

9.2 Тройной интеграл, его свойства. Вычисление тройного интеграла в

декартовой, цилиндрической и сферической системах координат. Приложение

кратных интегралов к решению геометрических, механи­ческих и физических

задач.

9.3 Поверхностные интегралы 1-го и 2-го рода, вычисление. Формулы Гаусса-

Остроградского, Стокса.

9.4 Скалярное поле и его характеристики. Векторное поле. Векторные линии и

трубки, их дифференциальные уравнения. Поток векторного поля через открытую и

замкнутую поверхность, его свойства, вы­числение.

9.5 Дивергенция векторного поля, физический смысл, свойства, вы­числение.

Теорема Остроградского.

9.6 Ротор векторного поля. Физический смысл, свойства, вычисление. Линейный

интеграл, циркуляция вектора поля по контуру, вычисле­ние. Теорема Стокса.

9.7 Векторные дифференциальные операции первого и второго поряд­ков. Оператор

«набла», свойства, действия с оператором. Основные типы векторных

полей: соленоидальное, потенциальное, гармоническое, их характеристики.

Потенциал векторного поля, его вычисление. Основная теорема векторного

анализа.

10. Ряды. Преобразование Фурье (42 часа)

10.1. Числовые ряды. Сходимость и сумма ряда. Геометрическая про­грессия.

Необходимое условие сходимости ряда. Простейшие дейст­вия над рядами. Ряды с

положительными членами.

10.2. Теоремы сравнения. Признаки сходимости Даламбера, Коши. Ин­тегральный

признак сходимости ряда.

10.3. Оценка остатка ряда с помощью интегрального признака.

Знако­чередующиеся ряды. Теорема Лейбница, оценка остатка ряда.

Знако­переменные ряды. Абсолютно и условно сходящиеся ряды. Теорема о

сходимости абсолютно сходящегося ряда. Ряды с комплексными чле­нами .

10.4. Функциональные ряды, область сходимости. Равномерная сходи­мость.

Признак Вейерштрасса.

10.5. Степенные ряды. Теорема Абеля. Круг сходимости, интервал и радиус

сходимости для рядов с действительными членами. Теорема о равномерной

сходимости степенного ряда. Непрерывность суммы. Ин­тегрирование и

дифференцирование степенных рядов.

10.6. Ряд Тейлора. Теорема о единственности разложения функции в степенной

ряд. Достаточные условия разложимости функции в ряд Тейлора. Применение

степенных рядов к решению дифференциальных уравнений. Приближенные

вычисления.

10.7. Ряд Фурье. Коэффициенты Фурье. Приближение в среднем. Свой­ства

минимальности коэффициентов Фурье. Теорема о сходимости в среднем и

поточечной сходимости тригонометрических рядов Фурье.

10.8. Понятие ортонормированной системы функций. Разложение в ряд Фурье четных и

нечетных функций/ заданных на интервале (-ЗТ,^Г) . Разложение в

тригонометрический ряд Фурье функций, заданных на интервале (a, b).

Интеграл Фурье. Комплексная форма интеграла и ряда Фурье. Преобразование Фурье.

Синус- и косинус- преобразова­ния Фурье. Свойства преобразования Фурье.

Раздел 1. Матрицы и определители. Векторная алгебра. Ана­литическая

(СЛАУ)

Учебники: [1, гл.5, § 1-6], [10, дополнение к гл. 1],[16, гл. 6, 11, § 1].

Аудиторная работа: [2, N 14.4(6), 14.7(2), 14.21(9), 15.2(3), 15.5(1-3,9),

15.45(1,2), 15.65(1), 16.18(1,4,12,20), 17.2(1,3), 19.1(3,9)], [7, гл.2, §

1-3, N 1, 2(1,3), 3(1,3), 5, 19(1,2,4), 20(1,2), 22(13), 24(3,7), 25(1,4),

29(1)], [18, N 5, 11, 23, 55, 75, 82, 257, 260, 608, 609, 689, 700, 725],

[20, ч.1, гл.3, § 1-4, N 3.1, 3.8, 3.12, 3.55, 3.78, 3.80, 3.91, 3.106,

3.114, 3.121, 3.150, 3.187, 3.192, 3.198, 3.207, 3.210], [25, занятия

1(1.2.1, I.2.3, 1.2.9, 1.2.15), 2(2.2.2.-2.2.4)] 10(10.2.1.,10.2.4(6-

Д),10.2.5,10.2.7), 11(11.2.1(а,б,в), 11.2.2(а,б), 11.2.3(а,б),

II.2.4) , 12 (12.2.1 (а, б, в, г) , 1.2.2.2, 12. 2. 4, 12. 2. 5 (в) ,12.2.7

(в) )].

Самостоятельная работа: [2, N 14.7(3,4), 14.21(11,12), 15.5(7,9,13),

15.45(4,7), 15.65(2,4), 16.18(6,12,20,21), 17.2(2,4,5),

19.1(2,3,5,8,10)], [7, гл.2, §1-3, N 2(2,4), 3(2,4), 19(3,5,6,8), 20(3,4),

22(3,4), 24(4,5,7,8), 25(3,5), 29(2)], [18, N 6, 11, 17, 25, 43, 44, 83, 84,

116, 118, 258-260, 270, 554, 690, 691, 698, 726, 727, 729], [20, ч.1, гл.3, §

1-4, N 3.2, 3.13, 3.56, 3.57, 3.79, 3.91, 3.85, 3.92, 3.110, 3.119, 3.124,

3.151, 3.152, 3.208, 3.211, 3.215], [25, задания 1, 2(2.3.1-2.3.5), 10, 11,

12].

Прямоугольной матрицей называется совокупность m∙ n чисел,

расположенных в таблице из m строк и n столбцов

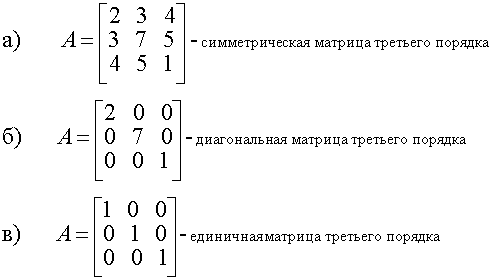
Числа aji , i=1,m, j=1,n, входящие в данную таблицу, называются

матричными элементами, а индексы i и j элемента aji указывают

(соответственно) номера строки и столбца, в которых расположен элемент.

Если m=n, то матрица называется квадратной. Квадратная матри­ца из n строк и

n столбцов, называется матрицей n-го порядка. Каждой матрице порядка n

ставится в соответствие число, которое называет­ся определителем или

детерминантом этой матрицы и обозначается од­ним из следующих символов

Числа aij (i, j=1,n) называются элементами определителя.

Если определитель матрицы равен 0, то матрица называется осо­бенной

(вырожденной), а если определитель отличен от 0 - то матри­ца неособенная

(невырожденная).

Квадратная матрица называется симметрической, если aij = aji,

т.е. равны элементы, симметричные относительно главной диагонали (главная

диагональ образована элементами aji , i=1,n

Диагональной называется матрица, у которой все элементы, не принадлежащие

главной диагонали равны 0.

Единичная матрица - это диагональная матрица, у которой все элементы

главной диагонали равны 1. Обозначается единичная матрица буквами Е или I.

Пример 1.1.1.

Две матрицы А и В называются равными, если они имеют одина­ковые

размерности и равные соответствующие элементы.

Матрица АТ , полученная из данной матрицы А заменой

каждой её строки столбцом с тем же номером, называется транспонированной

от­носительно А . Если матрица А имеет размеры m∙ n, то

матрица АТ имеет размеры n∙m.

Пример 1.1.2.

Линейными операциями над матрицами называются операции сложе­ния (вычитания)

и умножения на число. Сложение и вычитание опреде­ляется только для матриц

одинаковых размеров.

Суммой (разностью) двух матриц А={aij}mn и В={bij}mn называется

матрица С={cij}mn, для которой cij = aij ± bij , i=1,m, j=1,n.

Произведением матрицы А={aij}mn на число α называется матрица

В= α {aij}mn для которой bij = α aij , i=1,m, j=1,n.

Пример 1.1.3.

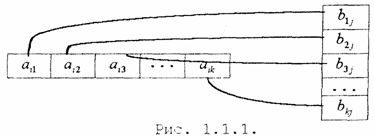
Даны матрицы

и число α = 4. Вычислить матрицы: С=А+В, D=A-B, М = а4

Умножение матриц А и В, т.е. получение произведения этих матриц С = АВ

, возможно лишь в том случае, когда число столбцов матрицы А равно

числу строк матрицы В . Такие матрицы называются согласованными.

Произведением двух согласованных матриц Аmk={aij}mk и Вkn={bij}kn

называется такая третья матрица Сmn={cij

}mn для кoторой каждый элемент cij

, i=1,m, j=1,n.вычисляется по формуле (рис. 1.1.1.)

Пример 1.1.4. Вычислить произведение матриц

Можно ли получить произведение BA ?

Число столбцов матрицы A(3) равно числу строк матрицы В(3).

Поэтому произведение АВ= С определено. Матрица С имеет

размер­ность 2х4, а её элементы вычисляются по формуле (1.1.2)

Произведение B∙A не определено, т.к. число столбцов матрицы B(4)

не равно числу строк матрицы А(2).

Определителем (1.1.1) матрицы второго порядка называется число

Определителем матрицы третьего порядка называется число

Студенту следует обратить внимание на правила треугольника и Сильвестра

вычисления определителей третьего порядка. Пример 1.1.5. Вычислить

определитель

Минором М ij (i, j=1,n) элемента а

ij определителя называется опре­делитель, который получается из

данного определителя вычеркиванием строки и столбца, на пересечении которых

находится элемент аij .

Алгебраическим дополнением Аij (i, j=1,n)

элемента аij определи­теля называется его минор взятый со

знаком (-1)i+j, т.е.

Аij=(-1)i+j Mij (1.1.3)

Пример 1.1.6. Записать миноры и алгебраические дополнения элементов

определителя примера 1.1.5.

и т.д. Всего можно записать 9 миноров и 9 алгебраических дополне­ний

элементов и определителя матрицы третьего порядка.

Замечание Определители матриц n-го порядка (n =1,2...) короче называют

определителями n-го порядка.

Свойства определителей:

1) определитель не изменится, если транспонировать матрицу опреде­лителя;

2) при перестановке двух соседних строк (столбцов) определитель меняет знак;

3) определитель с двумя одинаковыми строками (столбцами) равен 0;

4) общий множитель для элементов строки (столбца) можно вынести за знак

определителя;

5) определитель равен 0 , если все элементы строки (столбца) равны нулю;

6) определитель не изменится, если к элементам строки (столбца), прибавить

элементы другой строки (столбца), предварительно умно­жив их на один и тот же

множитель;

7) определитель равен сумме произведений элементов любой строки (столбца) на

их алгебраические дополнения

Например:

Пример 1.1.7. Вычислить определитель примера 1.1.5., исполь­зуя свойство 7

определителей (разложение произвести по элементам первого столбца)

По аналогии с формулой (1.1.4) вводятся определители n-го по­рядка

Пример 1.1.8. Используя свойства 1-7 определителей, вычислить определитель

четвертого порядка

Матрицей, обратной к матрице А, называется квадратная матри­ца

А-1, такая что A-1 А = Е

Если матрица А невырожденная (det A¹O), то обратная

матрица А-1 находится по формуле

где Aij (i, j =

1,n)

- алгебраические дополнения элементов аij (1.1.3)

Пример 1.1.9. Найти матрицу, обратную к данной матрице

Вычислим определитель матрицы А

По формуле (1.1.6) находим (вычисление алгебраических допол­нений элементов

матрицы А рассмотрено в примере 1.1.6) :

Проверка :

Студентам рекомендуется провести вычисление обратной матрицы методом

элементарных преобразований.

Рангом матрицы А размерности тхп называется наибольший из

порядков её миноров, отличных от нуля. Если ранг матрицы A равен r,

то это означает, что в матрице А имеется отличный от нуля ми­нор порядка

r , но всякий минор порядка большего, чем r, равен 0.

Ранг матрицы обозначается r(А) .

Свойства ранга матрицы А размерности т´ п

1) 0 ≤ r ≤ rnin(m,n);

2) r =0 тогда и только тогда, когда матрица нулевая;

3) для квадратной матрицы n-го порядка r=n тогда и только тогда, когда

матрица невырожденная;

4) ранг транспонированной матрицы равен рангу исходной матрицы;

5) ранг матрицы не изменится, если вычеркнуть (дописать) нулевую строку

(столбец);

6) ранг матрицы не изменится, если к элементам строки матрицы при­бавить

элементы другой строки матрицы, предварительно умноженные на некоторое число;

7) ранг матрицы не изменится, если переставить любые строки (столбцы) матрицы.

Пример 1.1.9. Найти ранг матрицы А

RgA=2 т.к. имеется отличный от нуля определитель второго порядка,

например

Студент должен уметь решать системы линейных алгебраических уравнений (в

дальнейшем СЛАУ)

1) по формулам Крамера и матричным методом (в случае, когда матри­ца

А системы невырожденная) ;

2) произвольные СЛАУ с использованием теоремы Кронекера-Капелли методом Гаусса.

Рассмотрим примеры на применение этих методов.

1) Предположим СЛАУ имеет невырожденную матрицу порядка п.

a11x1 + a12x2 + ... + a1nxn = b1

a21x1 + a22x2 + ... + a2nxn = b2

... ... ... ...

an1x1 + an2x2 + ... + annxn = bn

Правило Крамера. Если главный определитель СЛАУ отличен от нуля

(∆≠O), то СЛАУ имеет единственное решение, которое находится по

формулам

Матричный метод. Если матрица СЛАУ невырожденная, то решение СЛАУ может

быть найдено по формуле

X = A-1B

(1.1.8)

где матрица А-1 вычисляется по формуле (1.1.6 ), либо методом

эле­ментарных преобразований.

Пример 1.1.10. Решить СЛАУ

а) по формулам Крамера;

б) методом обратной матрицы

Запишем матрицу системы А, матрицу-столбец неизвестных X и

матрицу-столбец свободных членoв Х :

б)Воспользуемся формулой Х =А-1В, где матрица A-1 вычислена в при­мере 1.1.9.

2) Предположим, что матрица СЛАУ имеет размерность mxn. В этом случае СЛАУ

имеет вид

a11x1+a12x2+...+a1nxn=b1

a21x1+a22x2+...+a2nxn=b2

... ... ... ...

am1x1+am2x2+...+amnxn=bm __

Запишем расширенную матрицу системы А.

Теорема Кронекера-Капелли. Система линейных .алгебраических уравнений

совместна тогда и только тогда, когда ранг расширенной матрицы системы равен

рангу матрицы системы.

Для решения произвольных СЛАУ применяется метод Гаусса. Сущ­ность метода

Страницы: 1, 2, 3