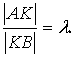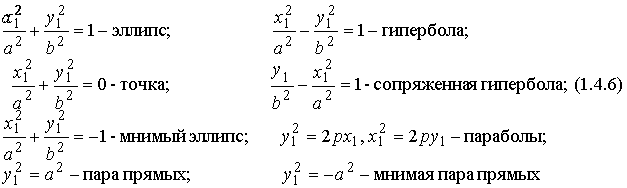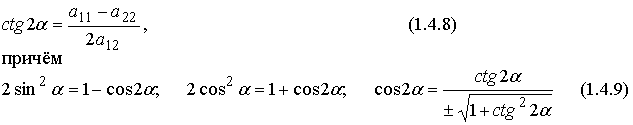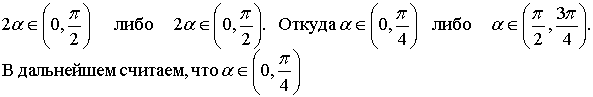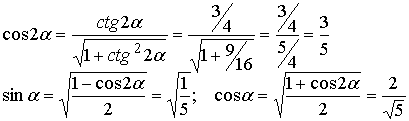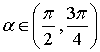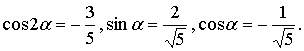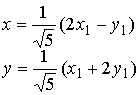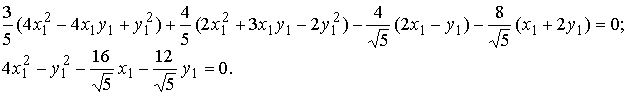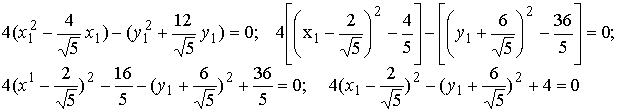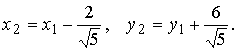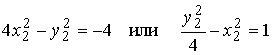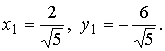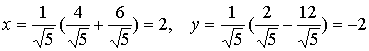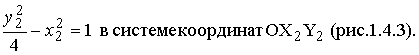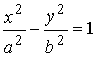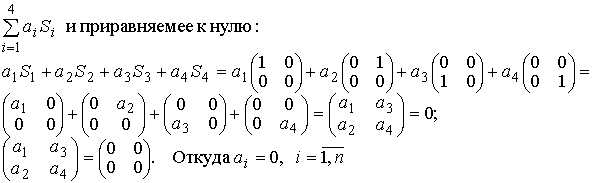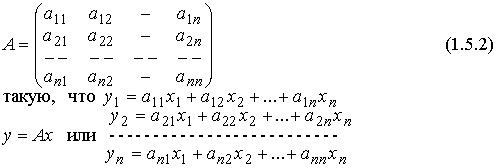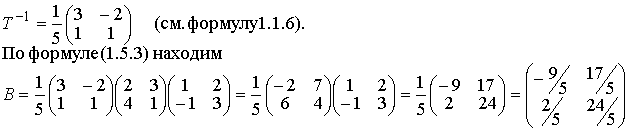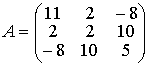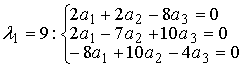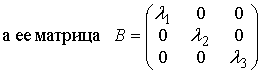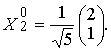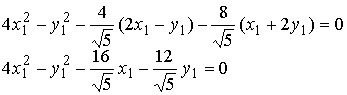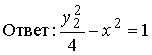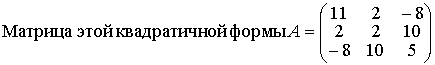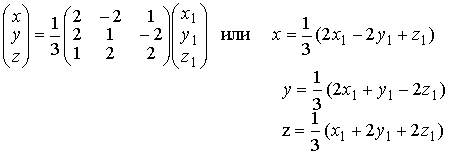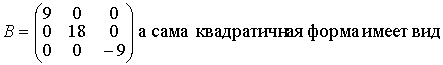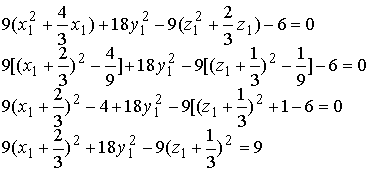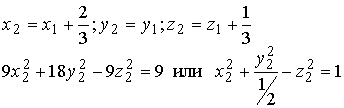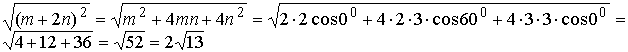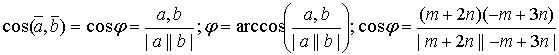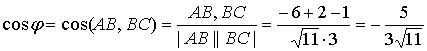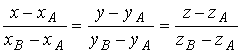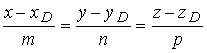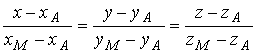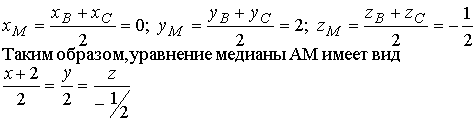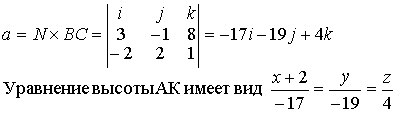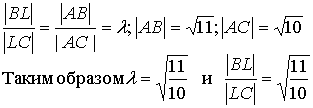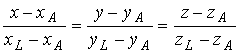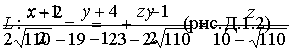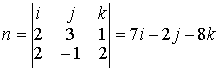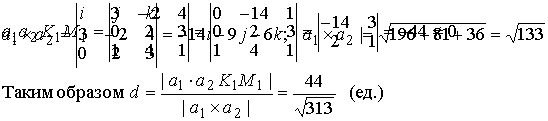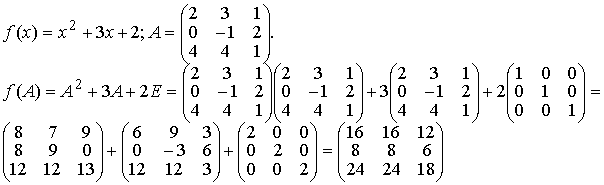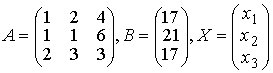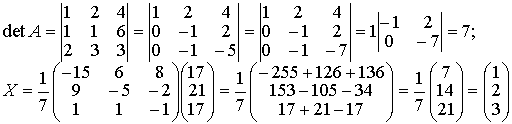Методические указания: Методические указания и рабочая программа по курсу «Высшая математика»

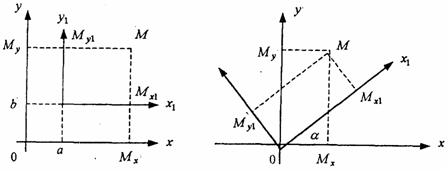
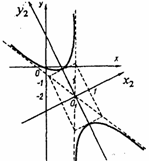
Методические указания: Методические указания и рабочая программа по курсу «Высшая математика»

Воспользуемся уравнением (1.3.29):

у = y2 + k(x-x2); y=0-5(x-4);

y=-5x +20, т.е. высота треугольника А1А2А3 ,

проведенная из вершины A2 совпадает с медианой, проведенной из этой

вершины.

Вопросы для самопроверки

1.Запишите условия перпендикулярности и параллельности:

а)прямых;

б)плоскостей;

в)прямой и плоскости.

2.Получите координаты точки К делящей данный отрезок АВ в отношении

3.Какие особенности имеет уравнение плоскости, если она:

а)параллельна осям координат ОХ; ОУ; OZ;

б)перпендикулярна осям координат ОХ; ОУ; OZ;

в)параллельна плоскостям ОХУ; OXZ; OYZ .

4. Как найти точку, симметричную точке М0(x0,у0

,z0) относительно плоскости Ах+ Ву+ Cz+D = 0 .

5. Составьте уравнение плоскости , проходящей через точку М0 (x0

,y0,z0) параллельно двум прямым с направляющими векторами

а1 и а2 , причем а1 ≠ а2

6.Получите нормальное уравнение плоскости.

7.Напишите уравнение плоскости, проходящей через точки М1 и М2 ,

параллельно вектору а .

8.Выведите формулы для нахождения расстояния от точки до прямой, между двумя

скрещивающимися прямыми.

9.Получите уравнение биссектрисы угла треугольника.

10.Получите формулу для нахождения угла между прямыми, лежащими в плоскости

ХОУ.

Тема 1.4. Преобразование координат на плоскости. Эле­ментарная теория линий

Тема выносится на самостоятельное изучение

Учебники: [ 1, гл.2, §4, гл.3, §1-3], [10, гл.6, §1-5] , [16, гл.2, §3, п.

10-13].

Самостоятельная работа : [ 2, N7.25, 7.38, 7.54, 8.1(1, 3, 6), 9.1(1,2),

9.3(1, 4), 9.4(1-3], [7, гл.3, N49, 50, 51, 54, 62(1,2), 63(1/2) ], [20, ч.1,

гл..2, N2.247, 2.249(1, 2), 2.256(a), 2.257, 2.258, 2.267, 2.269(a), 2.278,

2.279, 2.286/ 2.288(в), 4.226, 4.227 (в двух последних заданиях

преобразование координат проводить по формулам 1.4.1-1.4.3) ], [25, занятие

16(16.2.6-16.2.7) ].

Простейшими преобразованиями координат на плоскости есть пре­образование

поворота и параллельного переноса. Одна и та же точка имеет различные

координаты в разных системах декартовых коорди­нат. Существует связь между

координатами точки в различных системах координат.

Рис.1.4.1 Рис.1.4.2

Параллельный перенос. Заданы две системы координат: старая ОХУ

и новая О1Х1У1 (рис . 1. 4 .1) . Начало новой

системы координат находится в точке O1(а,в) .

Старые координаты х, у точки М через новые координаты x

1y1 вы­ражаются формулами

x=x1 +a, y=y1+b (1.4.1)

откуда х1 =х-а, y1 =y- b,

(1.4.2)

Поворот координатных осей. Новая система координат OX1Y1

полу­чена поворотом старой на угол α вокруг точки О (рис.1.4.2).Старые

координаты х, у точки М через новые координаты x1, y

1 выражаются фор­мулами

x=x1cosα - y1sinα

y=x1sinα + y1cosα

(1.4.3)

В общем случае, когда заданы преобразования параллельного переноса и поворота

осей координат, связь между старыми и новыми координа­тами имеет вид:

x=x1cosα - y1sinα+a

y=x1sinα + y1cosα+b

(1.4.4)

Студент должен уметь общее уравнение кривой второго порядка

a11х2 + 2а12 ху + а22 у2 + c1x + с2 у + d = 0, (1.4.5)

путем преобразования системы координат (параллельный перенос, по­ворот)

приводить к простейшему (каноническому) уравнению. В новой системе координат

уравнением кривой (1.4.5) будет одно из следую­щих канонических уравнений:

Общее уравнение второй степени (1.4.5) при повороте осей ко­ординат на угол

α преобразуется в уравнение

a΄11х12 + а΄22 у1

+ d΄ = 0 ( 1.4.7)

формулы преобразования координат имеют вид (1.4.3), угол α опре­деляется

по формуле

Уравнение (1.4.7) приводится к каноническим уравнениям (1.4.6)

выделением полных квадратов и применением фoрмул парал­лельного переноса

(1.4.1) .

Пример 1.4.1.Кривая второго порядка задана уравнением Зх2 +4xy-4x-8y= 0

Записать каноническое уравнение этой линии. В данном случае а11

= 3, 2а12 = 4, a22 = 0 . По формуле (1.4.8)

находим ctg2α=3/4 > 0 . Сле­довательно,

Тогда sinα >0 и cosα >0, cos2α >0. По формулам (1.4.9) вычисляем

Замечание: если предположить, что

то sinα > 0, cosα < 0, cos2α < 0 и по формулам (1.4.9) имеем:

Вычисленные значения sinα и cosα подставляем в (1.4.3):

Подставим полученные выражения в исходное уравнение и преоб­разуем его.

В последнем уравнении выделим полные квадраты

Используя формулы (1.4.1), положим

В новых координатах последнее уравнение имеет вид

Это уравнение определяет сопряженную гиперболу (действительная ось ОУ) с

полуосями а=1, b=2.

Построим гиперболу в новой системе координат O1Х2У2.

Вначале вы­числим старые координаты точки O1 в которой находится

центр гиперболы.

Рис.1.4.3

Для этой точки х2 = 0; у2 = 0.По формулам (1.4.1) находим

С помощью формул (1.4.3) вычисляем

Так, точка O1 имеет координаты O1 (2,-2).Через точку O

1 проводим ось OX 2 , для которой tgα = 1/2 и ось

OY2 перпендикулярно оси OX2. Строим гиперболу

Вопросы для самопроверки

1.Дайте определение эллипса, гиперболы, параболы.

2.Дайте определение директриссы и эксцентриситета кривых второго порядка.

3. Какие линии определяют уравнения 9х2 ± 4у2

= 36 . Вычислите параметры кривых.

4.Получите уравнения асимптот гиперболы.

5.Чему равен эксцентриситет для окружности?

6.Докажите,что произведение расстояний от произвольной точки гиперболы

до ее асимптот есть величина постоянная. а Ь

Тема 1.5.Некоторые сведения о линейных векторных пространствах. Собственные

числа и собственные векторы

Учебники: [16, гл.16, §1.2].

Аудиторная работа: [7, гл.2, §4, N34(1.2), 37(2), 39(1), 40(1,2), 41(1,2)],

[20, ч.1, гл.4, N4.83.4.86, 4.90, 4.106(a), 4.183], [25, занятия

14(14.2.1, 14.2.4), 15 (15.2.1, 15.2.4, 15.2.7)].

Самостоятельная работа: [7, гл.2, §4, N35, 37(1,3,4), 39(2), 40(3),

41(3,4)], [20, ч.1, гл.4, N4.84,4.87, 4.91, 4.92, 4.106(6), 4.184]/

[25, занятия 14(14.3.3, 15 (15.3.1, 15.3.5, 15.3.8, 15.3.9)].

В теории линейных векторных пространств обобщается понятие вектора,

введенного в курсе векторной алгебры.

Упорядоченная совокупность n чисел х={х1,х2,...хn

} называется n - мерным вектором, а числа х1, i=1,n,

составляющие эту совокупность на­зываются координатами вектора х;

n - мерный вектор можно рассматривать как матрицу-строку или матри­цу

столбец, состоящую из n элементов.

Линейным векторным пространством называется множество векто­ров (любой природы),

для которых определено два действия-сложение и умножение на произвольное число.

Линейные n-мерные векторные пространства будем обозначать Ln.

Если х={х1,х2,...хn} є Ln и у={у1, у2,... уп}є L, то

1. х = у , если хі = уі , i = 1, n

2. х+у = {х1 + y1,х2 + у2,. ...хп +уп „ } є Ln.

3. mх = {mx1, тх2,..., mxп} є Ln.

Приведенные определения позволяют рассматривать векторы обще­го вида не

обязательно геометрической природы.

Примеры линейных пространств:

а) множество геометрических векторов R3;

б) множество всех многочленов Рп(х), степени не превосходящей n;

в) множество матриц Amn, размерности mn;

г) пусть хi, i = 1,n -количество i-го сырьевого продукта,

измеренного в подходящих единицах, тогда векторы вида х={х1,х

2,...хn}могут задавать суточную потребность предприятия в

сырье, запасы сырья, хранящего­ся на складе и т.д.

Любая совокупность n линейно независимых векторов в n-мерном пространстве

образует базис в этом пространстве (определение линей­ной зависимости и

независимости векторов см. в теме 1.2).

Пример 1.5.1.Показать, что система векторов

образует базис в пространстве квадратных матриц

Представить матрицу А22 в виде линейной комбинации векторов Si, i=l,4.

Составим линейную комбинацию

Mы получили, что линейная комбинация векторов Si , i=1,n

равна нулю лишь в том случае, когда все коэффициенты этой линейной комбинации

равны нулю. Согласно определения (см. тему 1.2) векторы Si ,

i=1,n линейно независимы и могут быть использованы в качестве базисных

векторов.

Разложение матрицы А22 по базису Si , i=1,n имеет вид:

Линейное пространство называется евклидовьм, если в нем каж­дой паре

векторов х, y сопоставлено число, которое называется ска­лярным

произведением этих векторов, обозначается (х, у ) и удовле­творяет

аксиомам:

1.(х,у)=(у,х)

2. ( х1+ х2 , у ) = ( х1, у ) + (х2 , у)

3. (αх , у ) = α (х , у ) ;

4. (х, х )>0, х ≠ 0 и (x,x)=0, если х=0.

называется нормой вектора в евклидовом про­странстве.

Неравенство |(х,y)|≤║x

║х║y║называется неравенством Коши-Буняковского.

Два вектора евклидового пространства называются ортогональны ми, если их

скалярное произведение равно нулю, т.е. (х, у )=0.

Линейные преобразования. Если указано правило f, по

которому каждому вектору х линейного пространства Ln

ставится в соответствие единственный вектор у этого пространства,

то говорят, что в нем задано преобразование (отображение, оператор).

Преобразование f линейного пространства L называется

линейным (линейным оператором), если для любых векторов этого пространств х

1, х2 , х и любого λєR выполняются условия

Если линейное пространство L n-мерное пространство, а f

линейное преобразование (оператор) осуществляющее отображениe y=f(x), x(x

n) є L, тo можно построить матрицу этого преобразования

Замечание. Если вектор геометрический, то над ним ставится стрелка.

Пример 1.5.2. Показать, что преобразование y=a x x,

где а(а1,а2, а3) -постоянный

вектор, х(х1, x2, x3), y(y1,

y2, y3 ecть линейное в ли­нейном пространстве L3

и построить его матрицу А .

Чтобы доказать линейность преобразования y=a x x достаточно

проверить свойства (1.5.1).

Пусть x1, x2 є L3 , λєR ,

тогда у(х1+ х2) =а х (х1+ х

2) = а х х1 + а х х2

у(λх)= а х (λх)= λ (а х х), т.е. свойства

линейности (1.5.1) выполнены и преобразование y=a x x линейно.

Построим матрицу преобразования

Предположим в линейном пространстве Ln заданы базисы еi,

i=1,n и mi, i=1, а также матрица A линейного преобразования f

в базисе еi, i=1. Тогда матрица линейного преобразования в

базисе mi, i=1, будет иметь вид

B=T-1 AT,

(1.5.3)

где T -матрица перехода от старого базиса к новому.

Пример 1.5.3. В базисе e1 ,e2 преобразование f имеет матрицу

Найти матрицу преобразования f в базисе m1=е1 - е2 , т2=2ё2+3е2.

Матрица

(координаты векторов m1 и т2

записываются в столбцы, соответственно в первый и второй).

Собственные числа и собственные векторы матрицы линейного преобразования

(оператора)

Всякий ненулевой вектор х(а1,а2,...,аn

называется собственным вектором линейного преобразования, если

Ах=λx,

(1.5.4) где λ -некоторое число, называемое собственным значением

(числом) линейного преобразования.

Если матрица А имеет вид (1.5.2), то равенство (1.5.4) запи­сывается в

виде системы линейных алгебраических уравнений (Дц - Л)а^ -ь

a^a^+...+а^а^ = О

(a11- λ)a1+a12a2+...+a1nan=0

a21a1+(a22- λ)a2+...+a2nan=0

-----------------------------------

(1.5.5)

an1a1+an2a2+...+(ann- λ)an=0

Система (1.5.5), однородная СЛАУ, имеет отличные от нуля (нетривиальные)

решения только тогда, когда определитель равен нулю. Отсюда следует, что

det(A- λE)=0.

(1.5.6)

Уравнение (1.5.6) называется характеристическим уравнением матрицы данного

линейного преобразования. Каждый действительный корень λ уравнения

(1.5.6) является собственным числом. Соответствующие собственному числу

координаты собственного вектора находятся из системы (1.5.5) методом,

изложенном в теме 1.1 (см. пример 1.1.11).

Пример 1.5.4.Найти собственные числа и собственные векторы матрицы линейного

преобразования

Система однородных линейных алгебраических уравнений (1.5.5) для

нахождения собственных векторов имеет вид

(11-λ)а1+2а2-8а3=0

2а1+(2-λ)а2+10а3=0

(1.5.7)

-8а1+10а2+(5-λ)а3=0

Вычислим определитель (1.5.6) и решим соответствующее характеристическое

уравнение

Характеристическое уравнение имеет вид

λ3-18 λ2-81 λ+1458=0, а его решение λ

1=9, λ2=18, λ3=-9. Найденные

зна­чения λі, і=1,3 подставим в (1.5.7)

Решение этой системы х1= С(2,2,1)Т, С єR, а

соответствующий еди­ничный вектор х01 =(2/3, 2/3,

1/3) Т

При λ 2=18: х02=(-2/3, 1/3, 2/3)Т при λ3=-9 х03 =(1/3, -2/3, 2/3)

Решения систем линейных уравнений рассмотрены в теме 1.1 (см. пример 1.1.11).

Необходимо отметить следующие свойства собственных значений и собственных

векторов симметрической матрицы.

1.Корни характеристического уравнения вещественной симметрической матрицы

вещественны.

2.Собственные векторы вещественной симметрической матрицы, отве­чающие

различным собственным значениям ортогональны. (Проверьте на собственных

векторах матрицы примера 1.5.4).

Вопросы для самопроверки

1.Приведите примеры n-мерных векторов.

2.Что такое линейное векторное пространство, какое пространство

называется евклидовым?

З. Что такое базис в n -мерном пространстве?

4 . Как определяется линейное преобразование?

5.Докажите неравенство Коши-Буняковского.

6. Докажите неравенство ||x+y||≤||x||+||y||

7. При каком условии матрица линейного преобразования имеет диаго­нальный вид?

8.Сформулируйте алгоритм нахождения собственных векторов.

Тема 1. 6 . Квадратичные формы. Приведение к кано­ническому виду уравнений

линии и поверхности второго по­рядка

Учебники:[1, гл.3, §4],[10, гл.7, §2], [16, гл.11, §3].

Аудиторная работа:[2, N9.4(1, 3), 11.22(1)], [7,гл.3, §5, 6, N63(1,2)],

[20, ч.1, гл.4, §3, N4.226, 4.227, 4.233],[25, за­нятия 16(16.2.6(а,б)) ,

17(17.2.1, 17.2.2) ].

Самостоятельная работа: [2, N9.4(4-6), 11.22(2)], [7, гл.3, §5, 6,

N63(3-5)], [20, ч.1, гл.4, §3, N4.228, 4.289, 4.234],[25, задания

16(16.3.3(а,б, в) ) , 17(17.3.2, 17.3.3, 17.3.4(а,б,в)) ].

Квадратичной формой от трех переменных x,y,z называется одно­родный

многочлен второй степени относительно этих переменных.

F(x,y,z)= a11x2 + 2a12xу+ а22у

2 + 2a13xz+ 2a23yz+a22 z2

(1.6.1)

Если учесть, что а12 =a21, a13=a31, a23=a32 , то F(x,y,z) записывается

в виде

F(x, у, z) = а11х2 + а12ху + а

21ух + а22 у2 + a13xz + a31

zx + a23 yz + a32 zy + a22z2 .

называется матрицей квадратичной формы. Квадратичная форма имеет канонический

вид, если она содержит члены только с квадратами пе­ременных, т.е. аij

= 0; i,j = 1,3; i≠ j . Матрица (1.6.2) квадратичной формы

(1.6.1) будет иметь диагональный вид, если в трехмерном про­странстве перейти к.

новому базису, состоящему из собственных век­торов (см. тему 1.5) матрицы

А, при этом на главной диагонали бу­дут стоять собственные числа матрицы

А.

Квадратичная форма в новом базисе будет иметь вид

F(x1, y1, z1)=λ1x1

2 + λ2 y12 + λ

3z12

(1.6.3)

В случае двух переменных х, у квадратичная форма F(x,y) имеет вид

F(х,у) = а11х2 + 2а12 ху + а22

y2,

(1.6.4)

причем а12 = a21 .

Методы приведения квадратичной формы к каноническому виду применяются при

решении задач на приведение к каноническому виду уравнений кривых второго

порядка

a11x2 + 2а12 ху + а22 у2 + b1х + b2 y + с = 0

и уравнений поверхностей второго порядка

a11x2 + 2а12 ху + а22 у2 + 2a13 xz+2a23 yz+a22 z2 +b1х + b2 y +b3 z + с = 0

Канонические уравнения основных кривых второго' порядка были рассмотрены в

теме 1.4 (1.4.6)

Поверхности второго порядка делятся на центральные и нецен­тральные.

Канонические уравнения некоторых поверхностей второго порядка приведены ниже.

Уравнения центральных поверхностей второго порядка

λ=0-точка

λ =1-эллипс,

λ.=-1-мнимый эллипс.

λ =1-однополостный гиперболоид

λ =-1-двуполостный гиперболоид;

λ =0 эллиптический конус.

Нецентральные поверхности

λ =l-эллиптический параболоид,

λ =-1 гиперболический параболоид.

2.Цилиндрические поверхности:

λ=1- эллиптический цилиндр,

λ=1- гиперболический цилиндр.

-мнимый эллиптический цилиндр(уравнению не удовлетворяет ни одна точка),

-пара плоскостей,

г) х2 = 2ру, у2 = 2рх, z2 = 2рх , (1.6.12)

и т.д. параболические цилиндры .

Плоскости

х2 = λа2 , а ≠0, λ=1 пара параллельных плоскостей;

λ=-1 мнимые плоскости (уравнению не удовлетворяет ни одна точка

пространства);

λ=0 - пара совпадающих плоскостей.

Пример 1.6.1. Записать каноническое уравнение кривой второго порядка Зх2

+4xу - 4х- 8y = 0 (сравните с решением примера 1.4.1 темы 1.4).

Квадратичная форма, содержащаяся среди слагаемых левой части уравнения имеет

вид F(x,y)= Зх2+ 4xy , а ее матрица

Вычислим собственные числа и собственные векторы матрицы А (см.

тему 1.5)

Пусть собственные векторы Х

i(а1(i), а2(i)) i.=1,2,

где а1(i), а2(i -

коор­динаты. Система (1.5.5) для нахождения собственных векторов имеет вид

(3-λ)a1+2a2=0

2a1-λa2=0

(1.6.14)

Найдем собственные числа λ , решив характеристическое уравнение (1.5.6) .

Подставим первое собственное число λ1=4 в систему

(1.6.4).

и соответствующий единичный вектор X10 имеет вид

Подставим второе собственное число λ2=-1 в систему (1.6.14):

Перейдем в двумерное пространство R2 к новому базису состав­ленному

из собственных векторов матрицы А Х10 и Х

20. При этом мат­рица квадратичной формы В в новом

базисе будет иметь вид (1.5.3)

где матрица Т составлена из координат собственных векторов, запи­санных в

столбцы. Связь между старыми координатами х, у (в базисе i,

j ) и новыми координатами x1, y1 (в новом базисе)

реализуется по формуле

квадратичная форма в новом базисе имеет вид (1.6.3) (случай двух переменных)

F(x1, y1) = 4x12 - у1

2 .

Запишем равнение кривой второго порядка в новых координатах, приведем подобные.

Уравнение совпало с уравнением, полученным в примере 1.4.1. темы 1.4 и

поэтому дальнейшие преобразования идентичны.

сопряженная гипербола с полуосями а=1, b=2.

Пример 1.6.2.Записать каноническое уравнение поверхности вто­рого порядка

11x2 + 4ху + 2y2 - 16xz + 20yz + 5z2 + 6x + l2y -6=0.

Запишем квадратичную форму, входящую в состав левой части уравнения

F(x,y,z)=llxг + 4ху+2у2 - 16xz + 20yz + 5z2

Собственные числа этой матрицы λ1 = 9, λ2 = l8,

λ 3 = -9 и единичные cобст-венные векторы X10

= (2/3, 2/3, 1/3)T, X20 =(-2/3, 1/3, 2/3)Т

, X30=(1/3, -2/3, 2/3)Т

найдены в примере 1.5.4 (см. тему 1.5). Связь между координатами x, y,z в

старом базисе (i,j,k) и координатами x1,y1,z

1 в новом базисе (X10,X20

,X30) имеет вид

Выше записанная матрица, как в примере 1.6.1,образована из коорди­нат

собственных векторов, записанных в столбцы. Матрица квадратичной формы В

в новом базисе - диагональная

F(x,y,z) =9x12 +18y12 -9z12

Запишем уравнение поверхности второго порядка в новых коорди­натах, приведем

подобные члены и выделим полные квадраты

9x12 +18y1 2 - 9z12 + 2(2x1 - 2y1 + z1) + 4(2x1 +y1 -2z1) - б = 0;

9x12 + I8y12 - 9z12 +12x1 - бz1 - б = 0;

Перейдем к новым координатам (параллельный перенос)

Полученное уравнение является каноническим уравнением однополо стного

гиперболоида (1.6.7) с параметрами а =1, b =√2/2, с=1.

После изучения материала, содержащегося в разделе 1, студент должен выполнить

контрольную работу N1.

Вопросы для самопроверки

1. Изобразите схематично основные поверхности второго порядка.

2. Может ли алгебраическая поверхность второго порядка представлять собою:

а) плоскость;

б) пустое множество?

Привести примеры.

3. Назовите типы и выпишите канонические уравнения цилиндрических

поверхностей второго порядка.

4.Докажите, что всякое уравнение F(x,y,z)=0, где F-однородный

многочлен второй степени, определяет конус с вершиной в начале ко­ординат .

После изучения тем 1.1-1.6 раздела 1 студенту необходимо вы­полнить

контрольную работу N1.

Дополнение 1.1.Образец выполнения и оформления контрольной работы N1

алгебры."

Задача N1.Вычислить :

a) |m+2n| ;

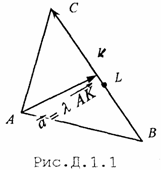
б) угол между векторами т+ п и -m+ п , если |т|= 2 ,|п| = 3 , (т,п)=60 o .

а)Согласно определения модуля |т+2п| =

б) угол между векторами a и b вычисляется по формулам

Вычислим отдельно числитель и знаменатель

(т+2n)(-m+3n)=-m2+mn+6n2 = -2∙2

|m+2n| =2√13 (см. пункт а) ;

Задача N2.Заданы координаты четырех вершин пирамиды ABCD .

А(-2,0,0), B(1,1,-1), С(-1,3,0), D(-1,0,2).

Вычислить АВ; (АВ,АС); площадь ΔAВС, объем пирамиды;

длину высоты DH пирамиды, проведенной к плоскости грани АВС.

Записать уравнения: прямой АВ; плоскости АВС; высоты пирамиды

DH; медианы AM треугольника АВС, высоты АК

треугольника АВС, биссектрисы AL треугольника АВС .

1. Вектор АВ имеет координаты: АВ (3,1,-1) . Поэтому его длина

рав­на: АВ= √9+l+l = √11 (ед) .

2.Угол φ между векторами АВ и АС определяется по формуле

(1.2.3).Вычислим длину вектора ВС :

BC=√4+4+1= 3 (ед) .

Скалярное произведение вычислялось по формуле (1.2.5)

3.Площадь треугольника АВС вычислена в примере 1.2.9.

4.Объем пирамиды ABCD вычислен в примере 1.2.10

5.Длина высоты DH пирамиды, проведенной из вершины D к

грани АВС также вычислена в примере 1.2.10.

6.Уравнение прямой АВ будем искать в виде (1.3.8), т.к. заданы

две точки этой прямой А и В.

Подставляя в последнее уравнение координаты точек А и В, получим (x+2)/3=y=-z

7.Уравнение плоскости АВС можно записать в виде (1.3.4), т.к.

за­даны координаты тpeх точек А,В,С

Уравнение плоскости АВС: 3x- y-8z+6 =0

8.Уравнение высоты пирамиды DH ищем в виде (1.3.6)

Координаты точки D известны/ а направляющий вектор прямой а(т,п,р)

коллинеарен вектору нормали к плоскости АВС . Вектор норма­ли к

плоскости АВС N имеет координаты N(3,-1,8)

(см. пункт 7 дан­ной задачи). Поэтому уравнение прямой DH имеет вид

9. Уравнение медианы AM ищем в виде (1.3.8)

Точка М- середина отрезка В С имеет координаты

10. Уравнение высоты АК ищем в виде

Направляющий вектор прямой АК, вектор a(m,n,p) перпендикулярен

вектору N(3,-1,8)-нормали к плоскости АВС и вектору BС(-2,2,1)

(рис.Д.1.1). Поэтому вектор а может быть вычислен по формуле (1.2.10)

11.Точка L-точка пересечения биссектрисы AL со стороной ВС

делит отрезок ВС на части, длины которых пропорциональны длинам

прилежащих сторон, т.е.

По формулам деления отрезка в данном отношении находим коор­динаты точки L

Уравнение биссектрисы AL ищем в виде (1.3.8)

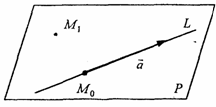
Подставляя в последнее уравнение координаты точек А и L, получим

Задача N3.Составить уравнение плоскости, проходящей через точку М (3,-1,2) и

прямую

Рис.Д.1.2

Уравнение искомой плоскости ищем в виде (1.3.1)

А(х-x0 ) +B(y-y0 )+C(z-z0 )= 0 , где (x0, у0, z0) координаты точки M0(1,-4,1),

расположенной на прямой L и принадлежащей плоскости Р .

Вектор нормали п к плоскости Р определим из условия n = М0

М1 x а , где М0М1 (2,3,1),

а (2, -1, 2 ) .

Таким образом п(А,В,С) = n(7,-2,-8) и уравнение плоскости имеет вид

7(х-1)-2(y+4)-8(z-1)=0

7х-2y-8z-7=0

Задача N4.Найти расстояние между прямыми

Прямая L1, проходит через точку M1(2,-2,1) и имеет направляющий вектор

a1 (3,-2,4). Уравнение прямой L2 запишем в виде

(1.3.8), пред­варительно определив какие-либо две точки, например: К1

(1,-6,0) и K2(1,0,9):

Направляющий вектор прямой L2 a2 (0,2,3). Прямые L

1 и L2 не параллель­ны, т.к. a1≠λa

2 , "λÎR. Проверим пересекаются ли прямые L1, и

L2 использовав условие (1.3.18)

Смешанное произведение векторов отлично от нуля, поэтому прямые L1, и

L2 не пересекаются, а являются скрещивающимися прямыми. Расстоя­ние

между скрещивающимися прямыми находим по формуле (1.3.20), предварительно

вычислив |a1 x a2| по формулам (1.2.10)

и (1.2.6)

Задача N5.Вычислить значение многочлена f(A) от матрицы А, если

Задача N6.Матричным методом решить систему линейных алгебраическиx уравнений.

x1+2x2+4x3=17

x1+x2+6x3=21

2x1+3x2+3x3=17

Решение системы находим по формуле (1.1.8) X= А-1В, где

а обратная матрица вычисляется по формуле (1.1.6) .

Таким образом, x1 = 1, x2 = 2, x3 = 3

Задача N7. Привести к каноническому виду уравнение линии второго порядка Зx

2 + 4xy - 4х- 8y = 0 .

Определить тип кривой.

Решение задачи приведено в примерах 1.4.1 и 1.6.1.

Метод решения студент выбирает сам.

Страницы: 1, 2, 3