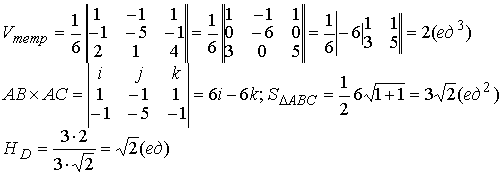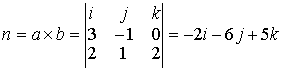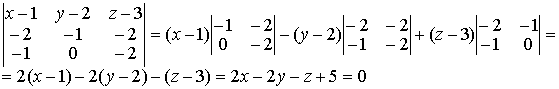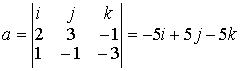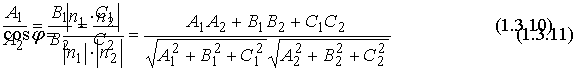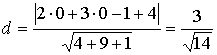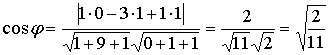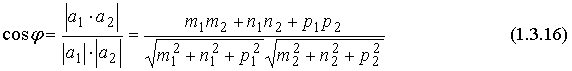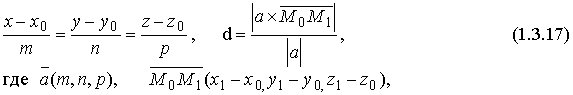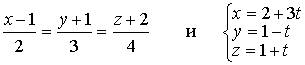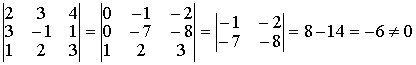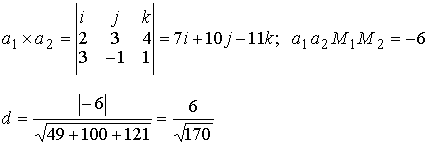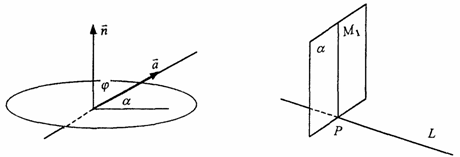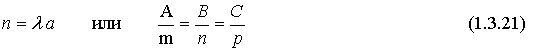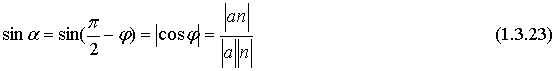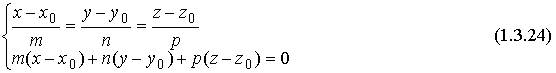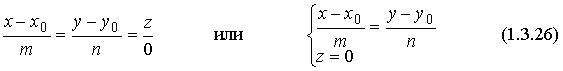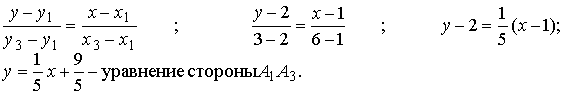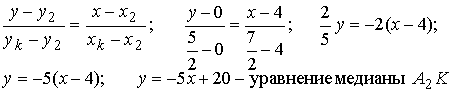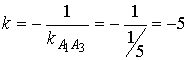|
РУБРИКИ |
Методические указания: Методические указания и рабочая программа по курсу «Высшая математика» |
РЕКОМЕНДУЕМ |
||
|
Методические указания: Методические указания и рабочая программа по курсу «Высшая математика»состоит в том, что расширенная матрица СЛАУ приводится к ступенчатому виду. Пример 1.1.11. Решить систему 2x1+5x2+2x3+3x4=4 7x1+4x2+x3+9x4=2 В этой системе m=3 - количество уравнений; n=4 - количество неизвестных. Запишем расширенную матрицу системы А и преобразуем ее к ступенчатому виду _ RgA=2, rgA=2. По теореме Кронекера-Капелли СЛАУ совместна. Укороченная СЛАУ имеет вид: 9x2+4x3+x4=8 В качестве базисных неизвестных выберем неизвестные х1 и x 2, а неизвестные, x3, x4 примем за свободные, полагая x3=C1, x4=C2. Тогда СЛАУ может быть записана в виде 9x2=8-4C1-C2 x3=C1 x4=C2 Откуда находим или окончательно получим Пример 1.1.12. Решить систему 2x1-x2+x3-x4=2 -x1+3x2-x3+3x4=0 2x1+4x2-3x3 +2x4=3 Система линейных алгебраических уравнений несовместна. Замечание. Однородные СЛАУ всегда совместны, т.к. ранги расширенной матрицы системы и матрицы системы совпадают. Вопросы для самопроверки 1. Какие матрицы называются равными? 2. В каких случаях возможно перемножение двух матриц ? 3. В каких случаях существуют произведения как АВ так и ВА? 4. Что называется минором и алгебраическим дополнением элементов матрицы ? В чем отличие между ними ? 5. Сформулируйте правило Крамера. 6. Как осуществляется транспонирование матрицы ? 7. В чем суть метода элементарных преобразований получения обратной матрицы ? 8. Что такое ранг матрицы ? 9. Что такое основная и расширенная матрицы системы ? 10. Сформулируйте и поясните на примерах теорему Кронекера-Капелли. Тема 1.2. Векторная алгебра Учебники: [1, гл.1, § 1-3], [10, гл.2]/ [16, гл.7]. Аудиторная работа: [2, N1.4, 1.10(1), 2.1(1), 2.2(1), 2.3(1)-2.8(1), 2.28, 3.1(1), 3.8, 3.19(1), 3.20(1), 3.23], [7, гл.3, N1(1), 2, 3, 8(1), 10, 11(1), 12(1), 14(1)], [20, ч.1, гл.2, N2.9, 2.35, .2.43, 2.78, 2.79, 2.100(a), 2.102, 2.106(a), 2.107, 2.118, 2.127(a), 2.132, 2.137], [25, занятия 2(2.2.9,2.2.10), 3(3.2.1, 3.2.3, 3.2.5-3.2.7), 4(4.2.4-4.2.6), 5(5.2.2, 5.2.5-5.2.7)]. Самостоятельная работа: [2, N1.5, 1.7, 1.10(2,3), 2.1(2-5), 2.2(2), 2.3(2, 3)-2.8 (2,3) , 2.29, 2.30, 3.1(2,3), 3.19(2,3), 3.20(2)], [7, гл.3, N1(2), 4, 6, 7, 8(2), 9, 11(2), 12(2), 14(2)], [20, ч.1, гл.2, N2.11, 2.32, 2.44-2.46, 2.82-2.84, 2.86, 2.100(б, в), 2.106(6,в), 2.108, 2.119, 2.127(6), 2.133, 2.134], [25, задания 2(2.3.6, 2.3.7), 3, 4, 5]. Для отвлеченного изображения конкретных векторных величин используются векторы. Вектором (геометрическим) называется направленный отрезок прямой. Два вектора называются равными, если они сонаправлены и имеют одинаковую длину. Положение начальной точки таких векторов не играет никакой роли. Поэтому геометрические векторы называются свободными. При изучении темы «Векторная алгебра» студенту следует обратить внимание на ниже рассмотренные вопросы. 1. Линейные операции над векторами (сложение, вычитание, умножение на число). Векторы необходимо уметь складывать как по правилу треугольника, так и по правилу параллелограмма. 2. Линейная комбинация векторов. Линейная зависимость и независимость векторов. Базисные векторы. Декартов базис. Пример 1.2.1. Указать при каких значениях α и β возможно равенство αa + βb = 0, где а° и b° единичные векторы (a0=a / |a|, b0=b / |b| ). Для решения приведенной задачи необходимо рассмотреть возможное расположение векторов а и b : Рис .1.2.1 Pис .1.2.2 Рис .1.2.3 a) векторы а и b сонаправлены (Рис. 1.2.1), тогда α=-β; b) векторы а и b имеют противоположное направление (рис.1.2.2). В этом случае α=β ; с) векторы а и b образуют между собой угол φ. При этом угол φ отличен от 0 и π радиан (рис.1.2.3). Приведенное в условии равенство возможно лишь при α=β=0. Рассмотренный пример дает представление о линейной зависимости и независимости векторов (важнейшее положение темы «Векторная алгебра»). Линейной комбинацией п векторов хi (i=1,n) называется сумма произведений этих векторов на действительные числа а i (i=1,n), а именно (В рассмотренном примере записана линейная комбинация 2х единичных векторов а° и b° ) . Векторы хi (i=l,n) называются линейно-зависимыми, если их линейная комбинация (1.2.1) равна нулю, а среди коэффициентов ai (i=l,n) имеется хотя бы один отличный от нуля. На рис. 1. 2 .1-1. 2 . 2 изображены два линейно зависимых вектора. Они могут быть расположены на одной прямой, либо на параллельных прямых. Два вектора, расположенные на одной либо на двух параллельных прямых, называются коллинеарными. Условие коллинеарности векторов а = λb , где λÎR. Если три вектора расположены в одной либо в параллельных плоскостях, то они называются компланарными. Компланарные векторы линейно зависимы. Необходимое и достаточное условие - компланарности векторов: с = αа+βb . Векторы xi (i=l,n) называются линейно-независимыми, если равенство нулю их линейной комбинации (1.2.1) возможно лишь в том случае, когда коэффициенты ai(i=l,n) одновременно равны 0. Случай двух линейно-независимых векторов представлен на рис. 1.2.3 (линейная комбинация αа+βb равна нулю лишь при одновременном обращении в ноль α и β) . Пример 1.2.2. Векторы а,b,с некомпланарны (линейно независимы). Доказать, что векторы m=a+2b-c, п=За-b+с и р=а+5b-Зс компланарны и найти их линейную зависимость. Приравняем к нулю линейную комбинацию векторов т,п,р (αт+ βn+γk = 0) и подставим в равенство разложения векторов т,п,р по векторам а, b,с . α(a+ 2b- c)+β(3a- b+ c)+γ(-a+5b-3c)=(α+3β - γ)a+(2 α - β+5 γ)b+(- α+ β-3 γ)c=0 Равенство нулю линейной комбинации векторов а,b,с возможно лишь в том случае, когда коэффициенты линейной комбинации равны нулю. Из этого условия получаем систему линейных алгебраических уравнений, которую решим методом Гауса (пример 1.1.11) Коэффициенты равной нулю линейной комбинации векторов т,п,р могут быть отличны от нуля, следовательно векторы т,п,р линейно зависимы (компланарны). Подставляя α, β, γ в равенствo αт+βп+γp=0 и сокращая на С, получим -2т+ n+k = 0 . С понятием линейной независимости векторов тесно связано такое фундаментальное понятие как базис. Базисом на плоскости Q называется любая упорядоченная пара неколлинеарных векторов, параллельныx плоскости Q. Любой вектор с, параллельный плоскости Q, можно представить в виде с= αа+ βb. Базисом в трехмерном пространстве называется любая упорядоченная тройка некомпланарных (линейно-независимых) векторов. Если а,b,с- базис в пространстве, то любой вектор d пространства можно единственным образом разложить по этому базису по формуле: d= αа+ βb+γc Декартовым базисом на плоскости (рмс 1.2.4) называются два единичных, взаимно-перпендикулярных вектора i и j (| i| = |j| =1, i^j ), совпадающих с положительным направлением осей ОХ и ОУ соответственно. рис.1.2.4 рис.1.2.5 Любой вектор плоскости а может быть единственным образом представлен в виде a=ax i+ay j , где числа аx и аy называются координатами вектора а . Декартовым базисом в пространстве (рис.1.2.5.) называются три единичных взаимноперпендикулярных вектора i,j,k, совпадающих с положительным направлением осей OX,OY и OZ соответственно. Любой вектор а может быть единственным образом представлен в виде a=ax i+ay+az k , где числа аx , аy , аz называются координатами вектора а. Если вектор a=АВ задается координатами начальной точки A(xa , ya, za ) и конечной B(xb, y b, zb ), то его координаты имеют вид: a=(xb-xa, yb-ya, zb-za ). Два вектора а и b равны в том и только в том случае, когда координаты их равны, т.е. ax=bx, ay=b y, az=bz. 3.Скалярное произведение векторов. Скалярным произведением векторов а и b называется число равное произведению длин этих векторов на косинус угла между ними, т.е. a b=|a||b|cos(a,b) (1.2.2 ) Из формулы (1.2.2) для ненулевых векторов можно вычислить косинус угла между векторами Длина вектора |а| определяется по формуле |a| = (1.2.4 ) Из свойств скалярного произведения следует обратить внимание на коммутативный (перестановочный) закон аb=bа. а =2т+ Зп , b = т- 2n , |т|=2 , |п|=3, (m,n)= π/3 . Угол между векторами вычисляется по формуле (1.2.3).
(2т+3n)(m-2n)=2mm-4-тп+Зпт-6пп=2тт-тп-6пп=2·2·3·cos0-2·3·cos( π/3)--6·3·3·cos0=12-3-54=-45; Предположим в пространстве задан декартов базис { i , j, k } и два вектора а = аx i+ ay j+ аz k , b = bx i + by j+ bz k . В декартовом базисе скалярное произведение векторов и длина вектора вычисляются по формулам: а b = axbx+ ayby + аzb z (1.2.5) |а| = Условие перпендикулярности векторов: аb=0 или axbx+ ayby + аzbz =0 (1.2.7) Условие коллинеарности векторов: a=λb или (1.2.8) Пример 1.2.4. При каком значении α векторы a(2,3,4) и b(3, α,-1) перпендикулярны? Используя (1.2.7), имеем ab=6+3α -4=0 или 3α =-2 , α =-2/3 Пример1.2.5.При каких значениях α и β векторы а(2,4, α) и b(4,β,1)коллинеарны? Используя условие коллинеарности векторов (1.2.8), имеем: 2/4=4/β=α/1. Откуда 4/β =1/2 или α/1=1/2, β = 8, а α =1/2 Пример 1.2. 6. Найти вектор b, коллинеарный вектору a(l,-2,-2) образующий с ортом j острый угол и имеющий длину |b| =15. Пусть вектор b имеет координаты bx , by, b z, Из условия коллинеарности (1.2.8) имеем b = λа или bx = λаx = λ , by = λаy =-2λ , bz= λа z=-2λ. По формуле (1.2.6) вычисляем Откуда |λ|=5 или λ=±5. Получаем два вектора b; b1 (5,-10,-10) и b2 (-5,10,10). Так угол между вектором b и ортом j острый, то cos(b,j)>0 и координата by >0. Поэтому в качестве вектора b выбираем вектор b2 т.е. b =-5 i+10 j+10k . 4. Векторное произведение векторов. Необходимо обратить внимание студентов на определение правой и левой троек векторов (рис.1.2.6 и 1.2.7). Рис.1.2.6 Рис.1.2.7 Тройка некомпланарных векторов a,b,c называется правой (рис.1.2.6) или левой (рис.1.2.7), если будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой (левой) руки. Векторным произведением векторов а и b называется вектор с, который обозначается символом с=а´b и удовлетворяет следующим трем условиям: 1) вектор с перпендикулярен плоскости векторов а и b; 2)образует с векторами а и b правую тройку; численно равна площади параллелограмма, построенного на векторах а и b, т.е. |с|= |a|×|b|sin(a b) (1.2.9) Из свойств векторного произведения следует обратить внимание на антикоммутативность, т.е. a´b=-b´a Пример 1. 2.7. Вычислить площадь треугольника, построенного на векторах а=2т+п и b = т- п , если |т|=2, |n|=1, (m,n)= π/6 Вычислим векторное произведение векторов a, и b и воспользуемся формулой (1.2.9) a´b =(2т+ п)-(т- n)= 2m´т- 2m´n+n´m-п´п =0-3m´n-0=-3m´n В декартовом базисе { i,j,k} векторное произведение векторов а(аx,аy,аz ) и b(bx, by ,bz) вычисляется по формуле Пример1.2.8. Найти координаты вектора b=(bx,by,bz ), если он перпендикулярен векторам a1 (2,-3,1) и a 2 (1,-2,3) и удовлетворяет условию; b(i +2j-7k) = 10. Вектор b перпендикулярен векторам a1 и a2. Поэтому его можнo искать в виде: Удовлетворим условию b(i + 2j-7k)=10; -7λ -10λ + 7λ =10; -10λ=10, λ=-1. Таким образом вектор имеет вид: b= 7i+5j+k. Пример 1.2.9.Вычислить площадь треугольника, вершины которого расположены в точках A(1,2,3), B(2,1,-1), С(3,-1,1). SΔABC =1/2 |ABxAC|.Вычислим координаты векторов АВ и АС и векторное произведение АВ´АС . 5.Смешанное произведение трех векторов. Смешанным произведением трех векторов а,b,с называется число, которое обозначается символом ахb-с (смешанное произведение иногда называют векторно-скалярным). Если векторы а,b,с некомпланарны, то смешанное произведение а ´b-с равно объему параллелепипеда, построенного на векторах а,b,с, взятому со знаком "+", если упорядоченная тройка векторов а,b,с -правая, и со знаком "-", если эта тройка - левая. Из свойств смешанного произведения трех векторов следует отметить следующие: 1)при круговой перестановке векторов смешанное произведение не меняется, т.е. ( aх b)× с = (сха)× b = (bхс)× а; 2)если в смешанном произведении поменять местами два соседних сомножителя, то произведение изменит знак, т.е. (aх b)× с = -(ах с)× b ; 3) смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны, т.е. условием компланарности векторов является равенство нулю смешанного произведения этих векторов. Смешанное произведение векторов в декартовом базисе {i,j,k}.Если а(ax, ay, az), b(bx, by, bz,) и с(сx, cy, cz), то Условие компланарности векторов Наиболее распространенные задачи, решаемые при помощи смешанного произведения: 1)найти объем параллелепипеда, построенного на векторах а,b,с: V = |а х b× с|, 2) найти объем тетраэдра, построенного на векторах а,b,с: V=1/6 (|а х b× с|) 3) проверить компланарны ли векторы а,b,с, если а х b× с=0, то векторы компланарны, если а х b× с¹ 0, то векторы некомпланарны; 4)проверить правую или левую тройку образуют векторы а,b,с, а х b× с=. <0 - тройка векторов левая. Замечание: смешанное произведение векторов а,b,с, как правило, записывают в виде а× b× с . Пример1.2.10. Вычислить длину высоты тетраэдра ABCD, проведенную из вершины D к основанию АВС, если вершины тетраэдра имеют координаты: А (1,2,0), B(2,1,1), С(0,-3,-1), D(3,3,4). Найдем координаты векторов, выходящих из вершины А: АВ(1,-1,1), AC(-1,-5,-1), AD(2,1,4), Vтетр=1/6(|АВ×АС×AD|); Vтетр =1/3(SDABC×HD); SDABC=1/2 (|AB´AC|); HD= Вопросы для самопроверки 1.Сформулируйте правила треугольника и параллелограма сложения векторов. 2.Укажите принципиальное различие в формулах для вычисления длины вектора в произвольном и декартовом базисах. З. Чему равно скалярное произведение базисных векторов в декартовом базисе? 4.Чему равно векторное произведение базисных векторов в декартовом базисе? 5.Запишите условие компланарности векторов. Приведите пример. 6.Можно ли построить треугольник на векторах а,b,а+b ? 7.Приведите пример условия, при выполнении которого из трех векторов a, b,с можно образовать треугольник. 8. Докажите, что объем тетраэдра вычисляется по формуле V= 9. Вычислите угол между векторами, совпадающими со скрещивающимися ребрами тетраэдра. 10.Как Вы считаете, произведение векторов axbxc (двойное векторное) является векторной величиной или скалярной? Тема 1.3. Прямая и плоскость Учебники:[1, гл.2, §1-3; 10, гл.4/ гл.5, §2-5; 16, гл.2, §1, 2, гл.10, §1, 2 (п.5), §3(п.7)]. Аудиторная работа: [2, 6.17(1-4), 6.18, 6.19(1), 6.20(3 6.21(1), 6.23(1), 6.25(1), 6.29, 6.34, 6.44(1)-6.47 (1), 6.50(1 6.51(1), 6.60(1) ,-6.62 (1) ,6.70(1) , 6.72J, [7, гл.З,Н15, 18(1— 19(1-4), 23(1),24(1), 26, 28(1), 30(1), 38, 41(1), 47(1) [20,ч.1, гл.2, N2.180(a)-2.184(a) , 2.185, 2.186, 2.189, 2.197(a 2.198, 2.199(a), 2.203(a)], [25, занятия 7(7.2.1-7.2.9), 8(8.2. 8.2.12), 6(6.2.1-6.2.2)] . Самостоятельная работа: [2, 6.19(2,3), 6.20(2-5 6.21(2,3), 6.23(2,3), 6.24, 6.25(2-5), 6.26, 6.30, 6.44(2 6.47(2), 6.50(2-4), 6.51(2,3), 6. 60 (2, 3)-6. 62 (2, 3) , 6.70(2,3 6.73], [7, гл.З,М16, 18(4- 13), 19(5-11), 20, 21, 23(2,3), 24(2,3 30(2), 41(2), 47(2,4), 48], [20, ч.1, гл.2, N2.180 (б)-2.184 (б 2.187- 2.188, 2.197(6), 2.200, 2.201, 2.203(6), 2.124], [2 занятия 7, 8, 6(6.2.1-6.2.4)]. При изучении аналитической геометрии в пространстве возникают затруднения, связанные с недостаточностью пространственных представлений. В таких случаях полезно пользоваться пространственными моделями (тетрадь-плоскость; карандаш, ручка-прямая, отрезок прямой) и использовать их при разборе теоретического материала наравне с рисунками, приведенных в задачниках. Различные виды уравнения плоскости 1.Уравнение плоскости, проходящей через данную точку М0(x0 ,у0,z0) перпендикулярно вектору n(А,В,С) : A(x-x0)+B(y-y0)+C(z-z0)=0 (1.3.1) Пример 1.3.1. Записать уравнение плоскости, проходящей через точку M0 (1, 2, 3), перпендикулярно вектору n(2,-1,4). Используя уравнение (1.3.1), получим 2(x-l)-l(y-2)+4(z-3)=0 или 2x-y+4z-l2-0. Пример 1. 3 . 2.Составить уравнение плоскости, проходящей через точку М0 (1,2,3) пареллельно векторам a(3,-1.,0) и b(2,l,2). Плоскость пареллельна векторам а и b, поэтому вектор нормали к плоскости n(А,В,С) равен векторному произведению векторов) а и b и находится по формуле (1.2.10): Уравнение искомой плоскости (1.3.1) имеет вид -2(x-l)-6(y-2)+5(z-3)=0 или -2x-6y+5z-l=0 . 2.Общее уравнение плоскости: Ax+By+Cz+D=0 (1.3.2) В этом уравнении коэффициенты А, В,С -координаты вектора п(А,В,С) перпендикулярного плоскости. 3.Уравнение плоскости в отрезках Числа a,b,c равны величинам направленных отрезков, отсекаемых на осях координат. 4.Уравнение плоскости, проходящей через три точки M1(x1 ,y1,z1), M2(x2,y2,z2 ) , М3(x3, у3, z3), не лежащие на одной прямой Пример 1.3.3.Составить уравнение плоскости, проходящей через три точки M 1(1,2,3), M2(-1,1,1) , М3(0,2,1) . В соответствии с уравнением (1.3.4) получаем т.е. 2x-2y-z+5=0 и есть уравнение искомой плоскости. Различные видах уравнений прямой в пространстве A2x+B2y+C2z+D2=0 (1.3.5) Прямая задана пересечением двух плоскостей с нормалями n1(A1, B1, C1) и n2 (A2, B2, C2) 2.Канонические (стандартные) уравнения прямой, проходящей через точку М0 (x0, y0, z0) и имеющей направляющий вектор а(т,п,р) Пример 1.3.4.Перейти от общих уравнений прямой 2x+3y-z+2=0 x-y-3z+6=0 к каноническим уравнениям. Прежде всего выберем какую- нибудь точку М0 , например М0 (0,0,2), удовлетворяющую общим уравнениям прямой. Если сразу не удается подобрать координаты точки М 0 , то эту точку можно найти из решения системы линейных уравнений (см. пример 1.1.11), которой задаются общие уравнения прямой. Направляющий вектор прямой а может быть выбран в виде a=n1 xn2 (см. 1.3.5), где n1(2,3,-l) и n 2(1,-1,-3) -нормальные векторы к плоскостям, пересечением которых и задается прямая 'Канонические уравнения прямой имеют вид 3. Параметрические уравнения прямой x = x0 + mt, y = y0 + pt, z = z0 + ut, t є R (1.3.7) Пример 1.3.5.В примере 1.3.4 от канонических уравнений прямой перейти к параметрическим уравнениям. Ряд равных отношений в канонических уравнениях прямой примера 1.3.4 приравняем к t: Откуда получим параметрическиe уравнения x=-t, y=t, z=2-t, t є R . 4.Уравнение прямой, проходящей через две точки M1(x1, y1, z1), М2(х2, у2, z2) . Замечание. В уравнениях прямой (1.3.6) и (1.3.8) допускаете равенство нулю одной или двух координат вектора а(т,п,р). В этом случае нуль в знаменателе воспринимается только лишь как информация о координатах вектора а . Задачи, относящиеся к плоскостям Пусть заданы две плоскости A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0 1.Взаимное расположение двух плоскостей: а)условие перпендикулярности плоскостей: A1A2+B1B2+C1C2 =0 (1.3.9) б)условие параллельности плоскостей 2.Угол между плоскостями: 3. Расстояние от точки М0 (х0, у0, z0) до плоскости Ax+By+Cz+D=0: Пример 1. 3 . 6 . Найти расстояние между параллельными плоскостям 2х+3у-z+1=0 2x+3y-z+4=0. Это расстояние равно расстоянию от любой точки одно плоскости до другой. Выберем на первой плоскости произвольную точку, например М0 (0, 0,1). По формуле (1.3.12) находим Пример 1.3.7.Найти угол между плоскостями х- 3у+z-1= 0 и y+z+2=0. По формуле (1.3.11) находим Замечание. Как правило, вычисляется острый угол между плоскостями. Задачи относящиеся к прямым в пространстве Пусть заданы две прямые в пространстве 1.Взаимное расположение двух прямых: а) условие перпендикулярности прямых: m1m2+n1n2+p1p2 =0 (1.3.14) б) условие параллельности прямых: 2.Угол между прямыми : 3. Расстояние от точки М (x1,y1,z1) до прямой а векторное произведение вычисляется по формуле (1.2.10). прямых. Прямые задаются уравнениями (1.3.13). Рассмотрим смешанное произведение a1 a2 M1M2 , a1 ≠ λa2 M1M2 = 0 (1.3.18) a1 a2 M1M2 ≠ 0 (1.3.19) то прямые скрещиваются. Смешанное произведение векторов вычисляется по формуле (1.2.11). Прямые заданы уравнениями (1.3.13). Если a1 a2 M 1M2 ≠ 0 то расстояние d между прямыми вычисляется по формуле Пример 1.3.8.Исследовать взаимное расположение прямых Первая прямая проходит через точку M1(1,-1,-2), a вторая прямая через точку М2(2,1,1) . Направляющие векторы прямых a1 (2,3,4) и a2(3,-1,1) . Вычислим смешанное произведение a1 a2 M1M2 Так как выполняется условие (1.3.19), то прямые скрещиваются. Пример 1.3.9.Вычислить расстояние между скрещивающимися прямыми примера 1.3.8. Используем формулу (1.3.20). Взаимное расположение прямой и плоскости Пусть плоскость задана уравнением (1.3.2), а прямая-уравнением (1.3.6) , либо уравнением (1.3.7), тогда n(A,B,C)— нормаль к плоскости, a(т,п,р) направляющий вектор прямой. Рис.1.3.1 Рис.1.3.2 1.Условие перпендикулярности прямой и плоскости 2.Условие параллельности прямой и плоскости: па = 0 или Am + Вп + Ср = 0 . (1.3.22) 3.Угол между прямой и плоскостью (рис.1.3.1) 4.Координаты точки пересечения прямой и плоскости находятся из системы уравнений (1.3.2) и (1.3.7), а именно x=x0+mt y=y0+nt (1.3.24) z=z0+pt 5. Проекция точки M1(x1,y1,z1) на прямую (рис. 1.3.2). Координаты точки Р определяются из системы где плоскость (α) проведена через точку M1 перпендикулярно прямой L. Прямая линия на плоскости Уравнение прямой линии на плоскости может быть получено из канонических уравнений прямой в пространстве (1.3.6), если положить z0 = 0 и р=0 В зависимости от условий задачи уравнение прямой на плоскости может быть записано в виде: a)y=kx+b- (1.3.27) уравнение прямой с угловым коэффициентом; б)ах+bу+с=0 - (1.3.28) общее уравнение прямой в)y=y0+k(x-x0)- (1.3.29) уравнение прямой, проходящей через точку Мо(хо, yо) и имеющей заданный угловой коэффициент k; уравнение прямой, проходящей через две заданные точки. Угол между двумя прямыми у = k1x+b1 и у = k2x+ b2 определяется по формуле Условия параллельности и перпендикулярности прямых имеет вид: k1 = k2 (параллельности) (1.3.32) k2 = -1/k1 (перпендикулярности) (1.3.33) Пример 1. 3.10. Треугольник задан координатами вершин A1(1,2), А 2(4,0), A3(6,3) . Написать уравнения: 1) стороны А1А3 ; 2) медианы, проведенной из вершины А2 ; 3) высоты, проведенной из вершины А2 1) Воспользуемся уравнением (1.3.30) 2) Пусть точка К -точка пересечения медианы треугольника, проведенной из А2 со стороной А1А3 . Точка К-середина отрезка А 1А3. Поэтому ее координаты равны полусумме координат концов отрезка, а именно Воспользуемся уравнением (1.3.30) 3)Высота, проведенная из вершины А2 перпендикулярна стороне А1 А3, поэтому угловой коэффициент k определяется из условия (1.3.33): |
|
© 2010 |
|
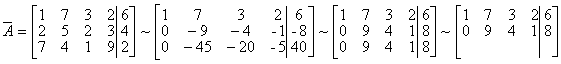
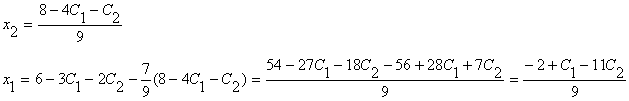
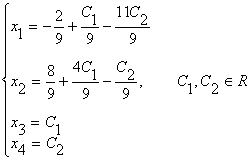


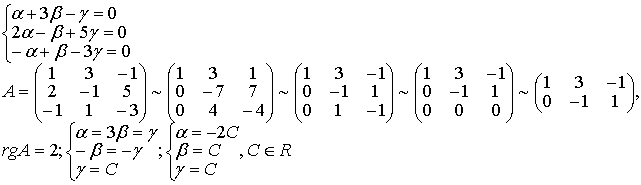


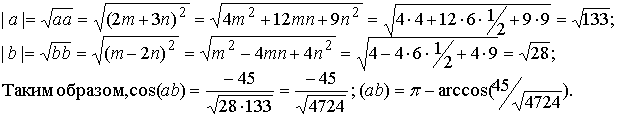
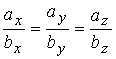

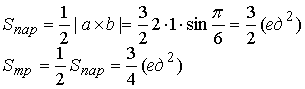

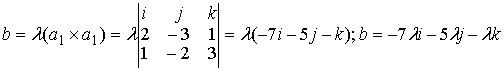
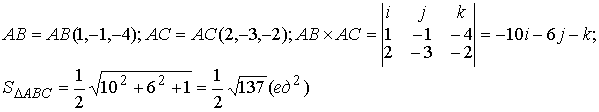

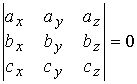 (1.2.12)
(1.2.12)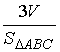 . Отсюда
. Отсюда