|
|
|
|
Диплом: Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
3. ПРОТОКОЛЫ РЕШЕНИЙ
3.1. Протоколы неверных решений
Задача 1.
Решить неравенство: 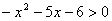 .
Решение:
Найдем корни квадратного уравнения .
Решение:
Найдем корни квадратного уравнения 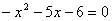 по теореме Виета: по теореме Виета:
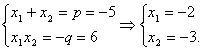 График функции График функции 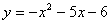 - это парабола, ветви которой направлены вниз: - это парабола, ветви которой направлены вниз:
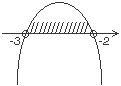
| Нужно отметить те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 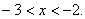 |
Задача 2.
Решить неравенство: 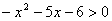 .
Решение:
Найдем корни квадратного уравнения .
Решение:
Найдем корни квадратного уравнения 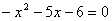 по теореме Виета: по теореме Виета:
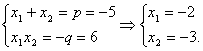 График функции График функции 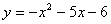 - это парабола. - это парабола.
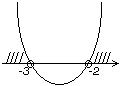
| Выберем те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 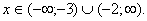 |
Задача 3.
Решить неравенство: 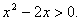 Решение:
Упростим выражение, сократив на x. Получим неравенство:
Решение:
Упростим выражение, сократив на x. Получим неравенство: 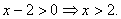 Следовательно, ответ:
Следовательно, ответ: 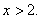 Задача 4.
Решить неравенство:
Задача 4.
Решить неравенство: 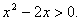 Решение:
Корни уравнения
Решение:
Корни уравнения 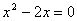 : : 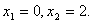 График функции
График функции 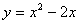 -
это парабола, ветви которой направлены вверх. -
это парабола, ветви которой направлены вверх.
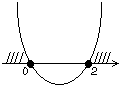
| Выберем те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 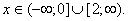 |
Задача 5.
Решить неравенство: 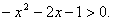 Решение:
Домножим неравенство на –1, получим:
Решение:
Домножим неравенство на –1, получим: 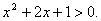 Выделим полный квадрат:
Выделим полный квадрат: 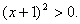 В левой части неравенства стоит неотрицательное число, а значит неравенство
верно при любых значениях x, кроме случая равенства, т.е.
В левой части неравенства стоит неотрицательное число, а значит неравенство
верно при любых значениях x, кроме случая равенства, т.е. 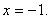 Запишем окончательный ответ:
Запишем окончательный ответ: 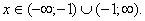 Задача 6.
Решить систему неравенств:
Задача 6.
Решить систему неравенств: 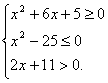 Решение:
Решаем каждое из неравенств системы в отдельности:
1.
Решение:
Решаем каждое из неравенств системы в отдельности:
1. 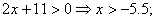 2.
2. 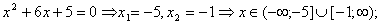
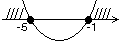 3.
3. 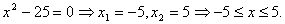
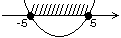
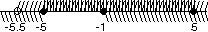 Ответ:
Ответ: 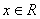 .
Задача 7.
Решить уравнение: .
Задача 7.
Решить уравнение: 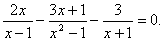 Решение:
Приведем дроби к общему знаменателю и отбросим знаменатель:
Решение:
Приведем дроби к общему знаменателю и отбросим знаменатель:
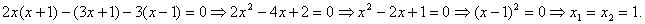 Ответ: x = 1.
Задача 8.
Решить уравнение:
Ответ: x = 1.
Задача 8.
Решить уравнение: 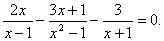 Решение:
ОДЗ:
Решение:
ОДЗ: 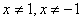 , т.к. знаменатель не должен обращаться в ноль.
Приведем все дроби к общему знаменателю: , т.к. знаменатель не должен обращаться в ноль.
Приведем все дроби к общему знаменателю:
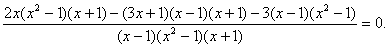 Приведем подобные и отбросим знаменатель:
Приведем подобные и отбросим знаменатель:
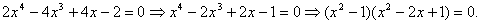 Получили
Получили 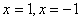 , но эти корни не входят в ОДЗ, поэтому ответ: решений нет.
Задача 9.
Решить уравнение: , но эти корни не входят в ОДЗ, поэтому ответ: решений нет.
Задача 9.
Решить уравнение: 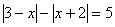 .
Решение:
Рассмотрим 4 возможных случая:
1. .
Решение:
Рассмотрим 4 возможных случая:
1. 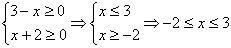 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 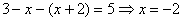 . Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2.
. Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2. 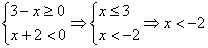 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 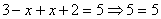 . Решение:
. Решение: 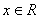 .
3. .
3. 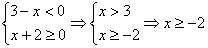 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 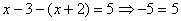 . Решений нет.
4.
. Решений нет.
4. 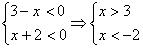 .
Получаем
уравнение .
Получаем
уравнение 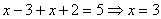 - не
удовлетворяет уравнению.
Объединяя найденные решения, получаем окончательный ответ: - не
удовлетворяет уравнению.
Объединяя найденные решения, получаем окончательный ответ: 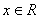 .
Задача 10.
Решить уравнение: .
Задача 10.
Решить уравнение: 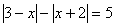 .
Решение:
Т.к. в уравнении 2 знака модуля, возможны 2 случая:
1. .
Решение:
Т.к. в уравнении 2 знака модуля, возможны 2 случая:
1. 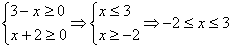 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 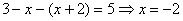 . Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2.
. Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2. 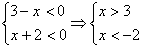 - этот случай невозможен.
Объединяя найденные решения, получаем окончательный ответ: - этот случай невозможен.
Объединяя найденные решения, получаем окончательный ответ: 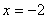 .
Задача 11.
Решить уравнение: .
Задача 11.
Решить уравнение: 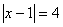 .
Решение:
Возможны 2 случая:
1. .
Решение:
Возможны 2 случая:
1. 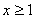 . Тогда уравнение примет вид: . Тогда уравнение примет вид: 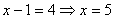 - корень исходного уравнения.
2. - корень исходного уравнения.
2. 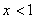 . Тогда уравнение примет вид: . Тогда уравнение примет вид: 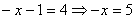 - корень исходного уравнения.
Ответ: - корень исходного уравнения.
Ответ: 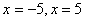 .
Задача 12.
Решить уравнение: .
Задача 12.
Решить уравнение: 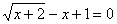 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 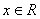 .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую: .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую:  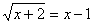 . Затем возводим в квадрат:
. Затем возводим в квадрат: 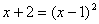 , причем т.к.
, причем т.к. 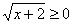 , то
для корректности возведения в квадрат необходимо, чтобы , то
для корректности возведения в квадрат необходимо, чтобы 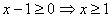 . Получим уравнение
. Получим уравнение 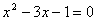 . Найдем его корни:
. Найдем его корни: 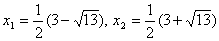 . Оба корня удовлетворяют ОДЗ, но только один
. Оба корня удовлетворяют ОДЗ, но только один 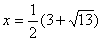 удовлетворяет дополнительному ограничению
удовлетворяет дополнительному ограничению 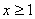 . Поэтому ответ:
. Поэтому ответ: 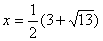 .
Задача 13.
Решить уравнение: .
Задача 13.
Решить уравнение: 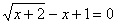 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 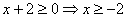 .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую: .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую:  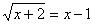 . Затем возводим в квадрат:
. Затем возводим в квадрат: 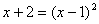 . Получим уравнение
. Получим уравнение 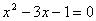 . Его корни:
. Его корни: 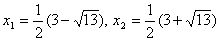 . Оба
корня удовлетворяют ОДЗ. Поэтому ответ: . Оба
корня удовлетворяют ОДЗ. Поэтому ответ: 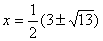 .
Задача 14.
Решить уравнение:
.
Задача 14.
Решить уравнение: 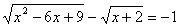 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 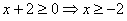 .
Выделим полный квадрат под первым знаком корня: .
Выделим полный квадрат под первым знаком корня: 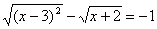 .
Получим уравнение: .
Получим уравнение: 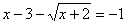 . Оставляем корень в левой части уравнения, а все остальные слагаемые переносим
в правую и умножим уравнение на -1:
. Оставляем корень в левой части уравнения, а все остальные слагаемые переносим
в правую и умножим уравнение на -1:  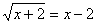 . Возведем обе части уравнения в квадрат с учетом
. Возведем обе части уравнения в квадрат с учетом 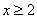 , получим
, получим 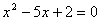 . Найдем
корни: . Найдем
корни: 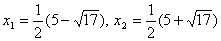 . Учитывая
ОДЗ и дополнительное ограничение . Учитывая
ОДЗ и дополнительное ограничение 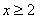 , получаем ответ:
, получаем ответ: 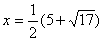 .
Задача 15.
Решить систему уравнений: .
Задача 15.
Решить систему уравнений: 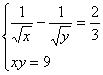 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 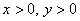 .
Из второго уравнения находим .
Из второго уравнения находим 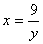 и подставляем в первое: и подставляем в первое: 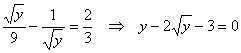 .
Делаем замену переменной: .
Делаем замену переменной: 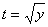 . Получаем квадратное уравнение относительно t:
. Получаем квадратное уравнение относительно t: 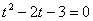 . Получим корни:
. Получим корни: 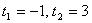 .
Имеем 2 случая:
1. .
Имеем 2 случая:
1. 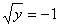 - это невозможно, т.к. - это невозможно, т.к. 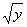 - неотрицательная величина.
2. - неотрицательная величина.
2. 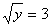 . Отсюда . Отсюда 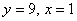 .
Ответ: (1; 9).
Задача 16.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. Первый
выходит из А на 6 часов раньше, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть .
Ответ: (1; 9).
Задача 16.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. Первый
выходит из А на 6 часов раньше, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть 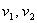 (км/ч) –
скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение
пешеходов. (км/ч) –
скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение
пешеходов.
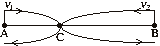
| Т.к. участок ВС первый прошел за 8 часов, то 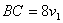 . Второй прошел расстояние СА за 9 часов, поэтому . Второй прошел расстояние СА за 9 часов, поэтому 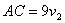 . . |
Из условия задачи имеем: 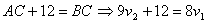 .
Выразим теперь время, затраченное пешеходами от начала движения до их встречи: .
Выразим теперь время, затраченное пешеходами от начала движения до их встречи: 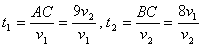 .
Т.к. первый вышел на 6 часов раньше, то: .
Т.к. первый вышел на 6 часов раньше, то: 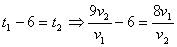 .
Сделаем замену: .
Сделаем замену: 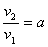 и
решим уравнение: и
решим уравнение: 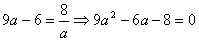 .
Это уравнение корней не имеет. Следовательно, ответ: такая ситуация невозможна.
Задача 17.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. Первый
выходит из А на 6 часов раньше, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть .
Это уравнение корней не имеет. Следовательно, ответ: такая ситуация невозможна.
Задача 17.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. Первый
выходит из А на 6 часов раньше, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть 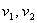 (км/ч) – скорости первого и второго пешеходов, S(км)=АВ. (км/ч) – скорости первого и второго пешеходов, S(км)=АВ.
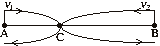
| Т.к. участок ВС первый прошел за 8 часов, то 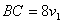 . Второй прошел расстояние СА за 9 часов, поэтому . Второй прошел расстояние СА за 9 часов, поэтому 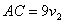 . . |
Т.к. первый до встречи в С со вторым прошел на 12 км меньше, то 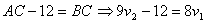 . Выразим теперь время, затраченное пешеходами от начала движения до их встречи:
. Выразим теперь время, затраченное пешеходами от начала движения до их встречи: 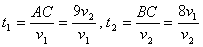 .
Т.к. первый вышел на 6 часов раньше, то:
.
Т.к. первый вышел на 6 часов раньше, то: 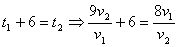 .
Сделаем замену: .
Сделаем замену: 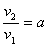 и решим уравнение: и решим уравнение: 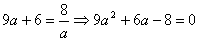 . Его корни: . Его корни: 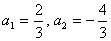 .
Получили 2 случая:
1. .
Получили 2 случая:
1. 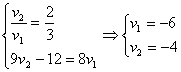 .
2. .
2. 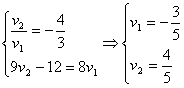 .
Значит,
1. .
Значит,
1. 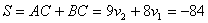 ;
2. ;
2. 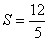 .
Т.к. расстояние не может быть отрицательным, то подходит только второй случай.
Ответ: .
Т.к. расстояние не может быть отрицательным, то подходит только второй случай.
Ответ: 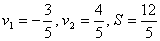 .
Задача 18.
Решить задачу: Две трубы, работая одновременно, наполняют бассейн за 12
часов. Одна первая труба наполняет бассейн на 10 часов медленнее, чем одна
вторая. За сколько часов наполняет бассейн одна вторая труба?
Решение:
Положим объем бассейна = 1. Пусть .
Задача 18.
Решить задачу: Две трубы, работая одновременно, наполняют бассейн за 12
часов. Одна первая труба наполняет бассейн на 10 часов медленнее, чем одна
вторая. За сколько часов наполняет бассейн одна вторая труба?
Решение:
Положим объем бассейна = 1. Пусть 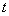 (ч) – время наполнения бассейна одной второй трубой. Тогда одна первая труба
наполнит бассейн за
(ч) – время наполнения бассейна одной второй трубой. Тогда одна первая труба
наполнит бассейн за 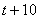 часов. Находим производительность этих труб:
часов. Находим производительность этих труб: 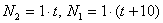 . За 12 часов совместной работы с общей производительностью
. За 12 часов совместной работы с общей производительностью 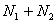 заполняется весь бассейн:
заполняется весь бассейн: 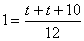 . Решаем полученное уравнение:
. Решаем полученное уравнение: 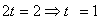 .
Ответ:
.
Ответ: 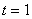 .
Задача 19.
Решить задачу: В ателье поступило по одному куску черной, зеленой и синей
ткани. Хотя зеленой ткани было на 9 м меньше, чем черной, и на 6 м больше,
чем синей, стоимость кусков была одинаковой. Сколько метров ткани было в
каждом куске, если известно, что стоимость 4.5 м черной ткани = общей
стоимости 3 м зеленой и 50 см синей?
Решение:
Пусть .
Задача 19.
Решить задачу: В ателье поступило по одному куску черной, зеленой и синей
ткани. Хотя зеленой ткани было на 9 м меньше, чем черной, и на 6 м больше,
чем синей, стоимость кусков была одинаковой. Сколько метров ткани было в
каждом куске, если известно, что стоимость 4.5 м черной ткани = общей
стоимости 3 м зеленой и 50 см синей?
Решение:
Пусть 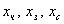 -количество черной, зеленой и синей ткани соответственно.
Известно: -количество черной, зеленой и синей ткани соответственно.
Известно: 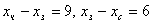 .
Используем формулу: .
Используем формулу: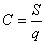 ,
где ,
где 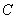 - цена ткани,
S – стоимость куска, q – количество ткани.
Пусть S = 1. Получим - цена ткани,
S – стоимость куска, q – количество ткани.
Пусть S = 1. Получим 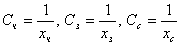 - цены тканей. Составим уравнение, связывающее эти стоимости:
- цены тканей. Составим уравнение, связывающее эти стоимости: 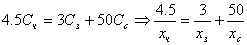 .
Выразим
.
Выразим 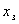 и и 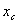 через через 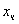 : : 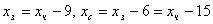 .
Подставляем в последнее уравнение: .
Подставляем в последнее уравнение: 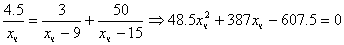 . .
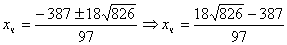 . Получили . Получили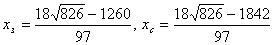 .
Ответ: .
Ответ: 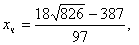 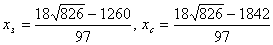 .
Задача 20.
Решить уравнение: .
Задача 20.
Решить уравнение: 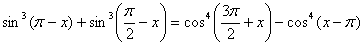 .
Решение:
По формулам приведения приведем все функции к одному аргументу: .
Решение:
По формулам приведения приведем все функции к одному аргументу: 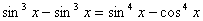 . Получили уравнение:
. Получили уравнение: 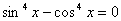 . По формулам сокращенного умножения разложим на множители:
. По формулам сокращенного умножения разложим на множители: 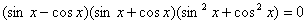 . По основному тригонометрическому тождеству
. По основному тригонометрическому тождеству 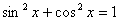 , поэтому остается решить уравнение:
, поэтому остается решить уравнение: 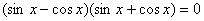 .
Рассмотрим 2 случая:
1.
.
Рассмотрим 2 случая:
1. 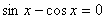 .
Разделим на .
Разделим на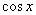 , причем , причем 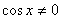 . Тогда имеем уравнение: tg x = 1. Следовательно,
. Тогда имеем уравнение: tg x = 1. Следовательно, 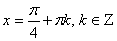 .
2.
.
2. 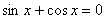 .
Разделим на .
Разделим на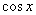 , причем , причем 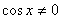 . Тогда имеем уравнение: tg x = -1. Следовательно,
. Тогда имеем уравнение: tg x = -1. Следовательно, 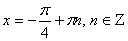 .
Получили ответ:
.
Получили ответ: 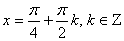 .
Задача 21.
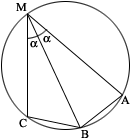
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1
см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.
Решение: .
Задача 21.
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1
см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.
Решение:
Страницы: 1, 2, 3, 4
|
|
|
|
|

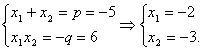 График функции
График функции 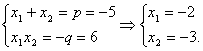 График функции
График функции 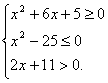 Решение:
Решаем каждое из неравенств системы в отдельности:
1.
Решение:
Решаем каждое из неравенств системы в отдельности:
1. 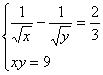 .
Решение:
ОДЗ:
.
Решение:
ОДЗ: 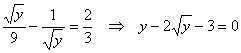 .
Делаем замену переменной:
.
Делаем замену переменной: 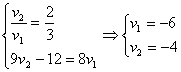 .
2.
.
2. 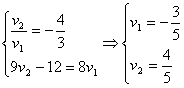 .
Значит,
1.
.
Значит,
1.