|
|
|
|
Диплом: Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Отрезки 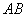 и и 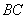 равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения
второе и получим:
равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения
второе и получим: 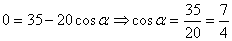 . Значит,
. Значит, 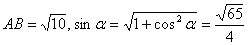 .
Треугольник .
Треугольник 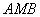 вписан
в окружность, следовательно, радиус данной окружности можно найти с помощью
теоремы синусов: вписан
в окружность, следовательно, радиус данной окружности можно найти с помощью
теоремы синусов: 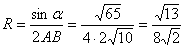 .
Ответ: .
Ответ: 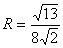 .
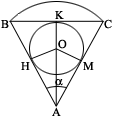
Задача 22.
Решить задачу: В сектор радиуса .
Задача 22.
Решить задачу: В сектор радиуса 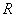 с центральным углом
с центральным углом 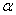 вписан круг. Найти его радиус.
Решение:
Треугольник ABC – равнобедренный, т.к. AB=AC=R. Найдем BC
по теореме косинусов:
вписан круг. Найти его радиус.
Решение:
Треугольник ABC – равнобедренный, т.к. AB=AC=R. Найдем BC
по теореме косинусов: 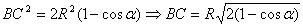 .
. 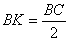 , т.к. АК
– высота треуг-ка АВС, следовательно, , т.к. АК
– высота треуг-ка АВС, следовательно, 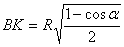 . Из прямоугольного треуг-ка АВК:
. Из прямоугольного треуг-ка АВК: 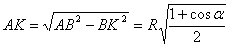 .
. 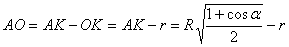 , где ОН=r
. Из прямоугольного треуг-ка АОН: , где ОН=r
. Из прямоугольного треуг-ка АОН: 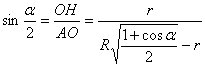 , значит, ответ:
, значит, ответ: 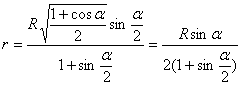 .
Задача 23.
Решить уравнение: .
Задача 23.
Решить уравнение: 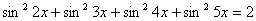 .
Решение:
ОДЗ: .
Решение:
ОДЗ: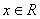 .
Применяя формулы понижения степени, приведем это уравнение к более простому
виду: .
Применяя формулы понижения степени, приведем это уравнение к более простому
виду:
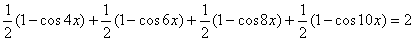 ,
, 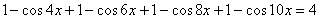 , ,
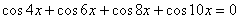 .
Отсюда, используя формулу преобразования суммы косинусов в произведение,
получаем: .
Отсюда, используя формулу преобразования суммы косинусов в произведение,
получаем: 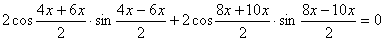 , ,
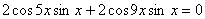 , ,
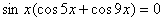 .
Рассмотрим 2 случая:
1. .
Рассмотрим 2 случая:
1. 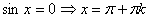 ;
2. ;
2. 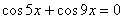 ,
следовательно, используя вновь формулу преобразования суммы косинусов в
произведение, имеем: ,
следовательно, используя вновь формулу преобразования суммы косинусов в
произведение, имеем:
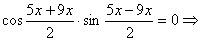 a)
a) 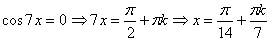 ;
b) ;
b) 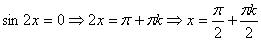 .
Таким образом, учитывая ОДЗ, получаем
Ответ: .
Таким образом, учитывая ОДЗ, получаем
Ответ: 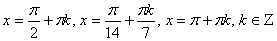 .
Задача 24.
Решить уравнение: .
Задача 24.
Решить уравнение: 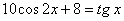 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 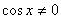 .
Введем новую переменную, положив t = tg x. Так как .
Введем новую переменную, положив t = tg x. Так как 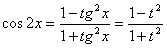 , то уравнение примет вид:
, то уравнение примет вид: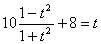 или
или 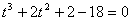 . Число 2
является корнем полученного уравнения, поэтому это уравнение можно
преобразовать следующим образом: . Число 2
является корнем полученного уравнения, поэтому это уравнение можно
преобразовать следующим образом: 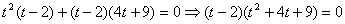 . Сократим на (t-2). Квадратный трехчлен во второй скобке не имеет
действительных корней. Следовательно, исходное уравнение не имеет корней.
Ответ: решений нет.
Задача 25.
Решить уравнение:
. Сократим на (t-2). Квадратный трехчлен во второй скобке не имеет
действительных корней. Следовательно, исходное уравнение не имеет корней.
Ответ: решений нет.
Задача 25.
Решить уравнение: 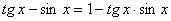 .
Решение:
Преобразуем уравнение следующим образом: .
Решение:
Преобразуем уравнение следующим образом:
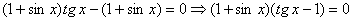 .
Рассмотрим 2 случая:
1. .
Рассмотрим 2 случая:
1. 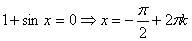 ;
2. ;
2. 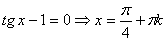 ;
Ответ: ;
Ответ: 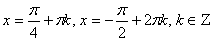 .
Задача 26.
Решить систему: .
Задача 26.
Решить систему: 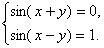 Решение:
Каждое из уравнений этой системы является простейшим, поэтому нетрудно
заметить, что
Решение:
Каждое из уравнений этой системы является простейшим, поэтому нетрудно
заметить, что
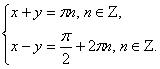 Решая последнюю систему, получаем
Ответ:
Решая последнюю систему, получаем
Ответ: 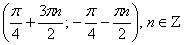 .
Задача 27.
Решить задачу: Основания трапеции 5 дм и 40 см. Найти длину отрезка,
соединяющего середины диагоналей.
Решение: .
Задача 27.
Решить задачу: Основания трапеции 5 дм и 40 см. Найти длину отрезка,
соединяющего середины диагоналей.
Решение:
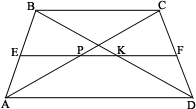
| Пусть ABCD – трапеция, точка Р – середина диагонали АС, точка К – середина диагонали BD. |
Нетрудно заметить, что точки Р и К лежат на средней линии EF
трапеции. Так как ЕК – средняя линия треугольника ABD, то 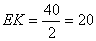 . Аналогично,
. Аналогично, 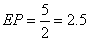 ,
поскольку является средней линией треугольника АВС. Следовательно, ,
поскольку является средней линией треугольника АВС. Следовательно, 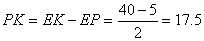 .
Ответ: 17.5 см.
Задача 28.
Решить задачу: Даны 2 стороны треугольника a, b и медиана
.
Ответ: 17.5 см.
Задача 28.
Решить задачу: Даны 2 стороны треугольника a, b и медиана 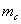 , проведенная к стороне c. Найти сторону с.
Решение:
, проведенная к стороне c. Найти сторону с.
Решение:
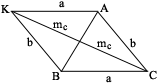
| Достроим треугольник АВС до параллелограмма АВСК. При этом 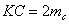 . По свойству параллелограмма сумма его диагоналей равна сумме его сторон. Поэтому из равенства . По свойству параллелограмма сумма его диагоналей равна сумме его сторон. Поэтому из равенства 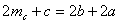 получаем получаем |
Ответ: 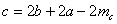 .
Задача 29.
Решить задачу: Даны 2 стороны треугольника a, b и медиана .
Задача 29.
Решить задачу: Даны 2 стороны треугольника a, b и медиана 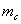 , проведенная к стороне c. Найти сторону с.
Решение:
Воспользуемся формулой
, проведенная к стороне c. Найти сторону с.
Решение:
Воспользуемся формулой
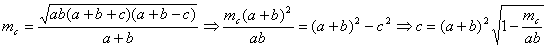 .
Ответ:
.
Ответ: 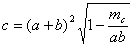 .
Задача 30.
Решить задачу: Несколько рабочих выполняют работу за 14 дней. Если бы их
было на 4 человека больше и каждый работал в день на 1 час больше, то та же
работа была бы сделана за 10 дней. Если бы их было еще на 6 человек больше и
каждый работал бы еще на 1 час в день больше, то эта работа была бы сделана
за 7 дней. Сколько было рабочих, и сколько часов в день они работали?
Решение:
Пусть w - число рабочих, х – число часов их работы в день.
Пусть вся работа равна единице, а у – производительность (в час)
каждого рабочего.
Тогда один рабочий за х часов (т.е. в день) выполняет ху единиц
работы, а w рабочих за 14 дней выполнят 14wxy единиц работы.
Согласно условию 14wxy = 1.
Аналогично, если рабочих стало w + 4, и они работают каждый день х + 1 час, то
10(w + 4)(x + 1)y = 1.
Для случая, когда рабочих еще на 6 человек больше (т.е. w + 6), и они
работают еще на час дольше (т.е. х + 1 часа) каждый день, получаем
уравнение 7(w + 6)(x + 1)y = 1.
Из системы .
Задача 30.
Решить задачу: Несколько рабочих выполняют работу за 14 дней. Если бы их
было на 4 человека больше и каждый работал в день на 1 час больше, то та же
работа была бы сделана за 10 дней. Если бы их было еще на 6 человек больше и
каждый работал бы еще на 1 час в день больше, то эта работа была бы сделана
за 7 дней. Сколько было рабочих, и сколько часов в день они работали?
Решение:
Пусть w - число рабочих, х – число часов их работы в день.
Пусть вся работа равна единице, а у – производительность (в час)
каждого рабочего.
Тогда один рабочий за х часов (т.е. в день) выполняет ху единиц
работы, а w рабочих за 14 дней выполнят 14wxy единиц работы.
Согласно условию 14wxy = 1.
Аналогично, если рабочих стало w + 4, и они работают каждый день х + 1 час, то
10(w + 4)(x + 1)y = 1.
Для случая, когда рабочих еще на 6 человек больше (т.е. w + 6), и они
работают еще на час дольше (т.е. х + 1 часа) каждый день, получаем
уравнение 7(w + 6)(x + 1)y = 1.
Из системы
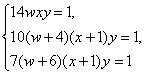 надо найти w, x.
Приравняв левые части первого и второго, а также первого и третьего уравнений
и упростив, получим систему
надо найти w, x.
Приравняв левые части первого и второго, а также первого и третьего уравнений
и упростив, получим систему
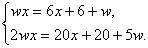 Отсюда легко получается, что
Отсюда легко получается, что 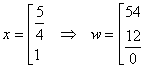 . Следовательно, второе значение х не подходит. Поэтому получили
Ответ: всего было 54 рабочих; они работали 1,25 часов в день.
3.2. Ответы (протоколы верных решений)
Задача 1.
Решить неравенство:
. Следовательно, второе значение х не подходит. Поэтому получили
Ответ: всего было 54 рабочих; они работали 1,25 часов в день.
3.2. Ответы (протоколы верных решений)
Задача 1.
Решить неравенство: 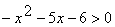 .
Решение:
Найдем корни квадратного уравнения .
Решение:
Найдем корни квадратного уравнения 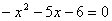 по теореме Виета: по теореме Виета:
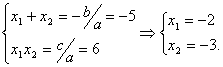 График функции График функции 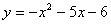 - это парабола, ветви которой направлены вниз: - это парабола, ветви которой направлены вниз:
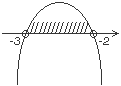
| Нужно отметить те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 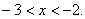 |
Задача 2.
Решить неравенство: 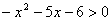 .
Решение:
Найдем корни квадратного уравнения .
Решение:
Найдем корни квадратного уравнения 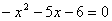 по теореме Виета: по теореме Виета:
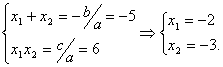 График функции График функции 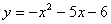 - это парабола, ветви которой направлены вниз: - это парабола, ветви которой направлены вниз:
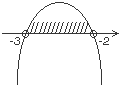
| Нужно отметить те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 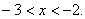 |
Задача 3.
Решить неравенство: 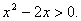 Решение:
Корни уравнения
Решение:
Корни уравнения 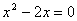 : : 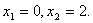 График функции
График функции 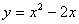 -
это парабола, ветви которой направлены вверх. -
это парабола, ветви которой направлены вверх.
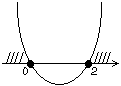
| Выберем те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 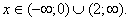 |
Задача 4.
Решить неравенство: 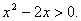 Решение:
Корни уравнения
Решение:
Корни уравнения 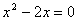 : : 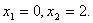 График функции
График функции 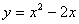 -
это парабола, ветви которой направлены вверх. -
это парабола, ветви которой направлены вверх.
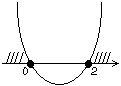
| Выберем те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 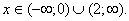 |
Задача 5.
Решить неравенство: 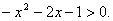 Решение:
Домножим неравенство на –1, получим:
Решение:
Домножим неравенство на –1, получим: 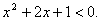 Выделим полный квадрат:
Выделим полный квадрат: 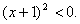 В левой части неравенства стоит неотрицательное число, а значит неравенство
неверно при любых значениях x, т.е. не имеет решений.
Запишем окончательный ответ: решений нет.
Задача 6.
Решить систему неравенств:
В левой части неравенства стоит неотрицательное число, а значит неравенство
неверно при любых значениях x, т.е. не имеет решений.
Запишем окончательный ответ: решений нет.
Задача 6.
Решить систему неравенств: 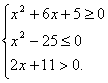 Решение:
Решаем каждое из неравенств системы в отдельности:
1.
Решение:
Решаем каждое из неравенств системы в отдельности:
1. 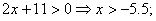 2.
2. 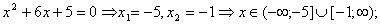
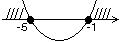 3.
3. 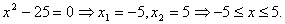
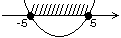 Для того, чтобы получить решение системы, возьмем пересечение всех полученных
интервалов.
Для того, чтобы получить решение системы, возьмем пересечение всех полученных
интервалов.
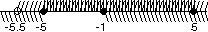 Ответ:
Ответ: 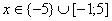 .
Задача 7.
Решить уравнение: .
Задача 7.
Решить уравнение: 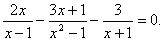 Решение:
ОДЗ:
Решение:
ОДЗ: 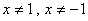 .
Приведем дроби к общему знаменателю и отбросим знаменатель: .
Приведем дроби к общему знаменателю и отбросим знаменатель:
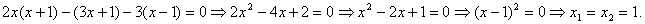 Но x=1 не входит в ОДЗ, поэтому ответ: решений нет.
Задача 8.
Решить уравнение:
Но x=1 не входит в ОДЗ, поэтому ответ: решений нет.
Задача 8.
Решить уравнение: 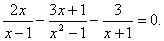 Решение:
ОДЗ:
Решение:
ОДЗ: 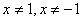 , т.к. знаменатель не должен обращаться в ноль.
Приведем дроби к общему знаменателю и отбросим знаменатель: , т.к. знаменатель не должен обращаться в ноль.
Приведем дроби к общему знаменателю и отбросим знаменатель:
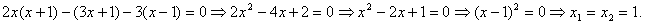 Но x=1 не входит в ОДЗ, поэтому ответ: решений нет.
Задача 9.
Решить уравнение:
Но x=1 не входит в ОДЗ, поэтому ответ: решений нет.
Задача 9.
Решить уравнение: 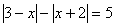 .
Решение:
Рассмотрим 4 возможных случая:
1. .
Решение:
Рассмотрим 4 возможных случая:
1. 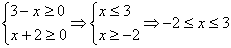 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 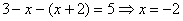 . Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2.
. Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2. 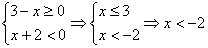 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 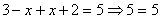 . Решение:
. Решение: 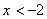 .
3. .
3. 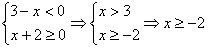 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 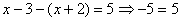 . Решений нет.
4.
. Решений нет.
4. 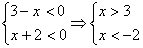 - этот случай не возможен.
Объединяя найденные решения, получаем окончательный ответ: - этот случай не возможен.
Объединяя найденные решения, получаем окончательный ответ: 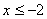 .
Задача 10.
Решить уравнение: .
Задача 10.
Решить уравнение: 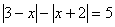 .
Решение:
Рассмотрим 4 возможных случая:
1. .
Решение:
Рассмотрим 4 возможных случая:
1. 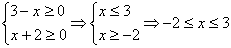 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 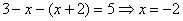 . Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2.
. Это значение удовлетворяет уравнению, поэтому является корнем данного
уравнения.
2. 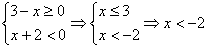 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 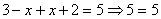 . Решение:
. Решение: 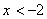 .
3. .
3. 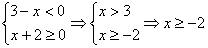 .
В
этом случае получаем уравнение .
В
этом случае получаем уравнение 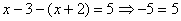 . Решений нет.
4.
. Решений нет.
4. 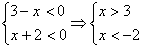 - этот случай не возможен.
Объединяя найденные решения, получаем окончательный ответ: - этот случай не возможен.
Объединяя найденные решения, получаем окончательный ответ: 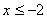 .
Задача 11.
Решить уравнение: .
Задача 11.
Решить уравнение: 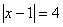 .
Решение:
Возможны 2 случая:
1. .
Решение:
Возможны 2 случая:
1. 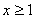 . Тогда уравнение примет вид: . Тогда уравнение примет вид: 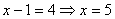 - корень исходного уравнения.
2. - корень исходного уравнения.
2. 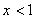 . Тогда уравнение примет вид: . Тогда уравнение примет вид: 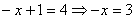 - корень исходного уравнения.
Ответ: - корень исходного уравнения.
Ответ: 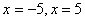 .
Задача 12.
Решить уравнение: .
Задача 12.
Решить уравнение: 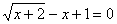 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 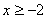 .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую: .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую:  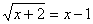 . Затем возводим в квадрат:
. Затем возводим в квадрат: 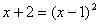 , причем т.к.
, причем т.к. 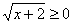 , то
для корректности возведения в квадрат необходимо, чтобы , то
для корректности возведения в квадрат необходимо, чтобы 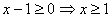 . Получим уравнение
. Получим уравнение 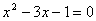 . Найдем его корни:
. Найдем его корни:
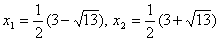 . Оба корня
удовлетворяют ОДЗ, но только один . Оба корня
удовлетворяют ОДЗ, но только один 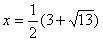 удовлетворяет дополнительному ограничению
удовлетворяет дополнительному ограничению 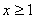 . Поэтому ответ:
. Поэтому ответ: 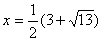 .
Задача 13.
Решить уравнение: .
Задача 13.
Решить уравнение: 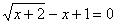 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 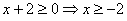 .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую: .
Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в
правую:  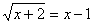 . Затем возводим в квадрат:
. Затем возводим в квадрат: 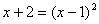 , причем т.к.
, причем т.к. 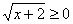 , то
для корректности возведения в квадрат необходимо, чтобы , то
для корректности возведения в квадрат необходимо, чтобы 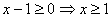 . Получим уравнение
. Получим уравнение 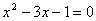 . Найдем его корни:
. Найдем его корни: 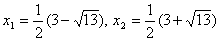 . Оба корня удовлетворяют ОДЗ, но только один
. Оба корня удовлетворяют ОДЗ, но только один 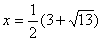 удовлетворяет дополнительному ограничению
удовлетворяет дополнительному ограничению 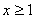 . Поэтому ответ:
. Поэтому ответ: 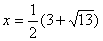 .
Задача 14.
Решить уравнение: .
Задача 14.
Решить уравнение: 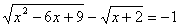 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 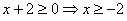 .
Выделим полный квадрат под первым знаком корня: .
Выделим полный квадрат под первым знаком корня: 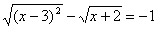 .
Получим уравнение: .
Получим уравнение: 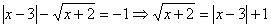 .
Рассмотрим 2 случая:
1. .
Рассмотрим 2 случая:
1. 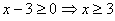 .
Получим .
Получим 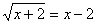 . Возведем
обе части уравнения в квадрат с учетом . Возведем
обе части уравнения в квадрат с учетом 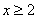 , получим
, получим 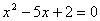 . Найдем
корни: . Найдем
корни: 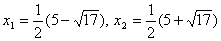 . Учитывая
ОДЗ и дополнительное ограничение . Учитывая
ОДЗ и дополнительное ограничение 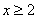 , получаем корень:
, получаем корень: 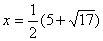 .
2. x<3. Получим
.
2. x<3. Получим 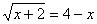 . Возведем обе части уравнения в квадрат с учетом
. Возведем обе части уравнения в квадрат с учетом 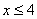 , получим
, получим 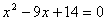 . Найдем
корни: . Найдем
корни: 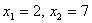 . Учитывая
ОДЗ и дополнительное ограничение . Учитывая
ОДЗ и дополнительное ограничение 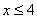 , получаем корень:
, получаем корень: 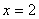 .
Учитывая ОДЗ, получаем ответ: .
Учитывая ОДЗ, получаем ответ: 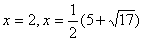 .
Задача 15.
Решить систему уравнений: .
Задача 15.
Решить систему уравнений: 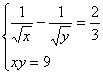 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 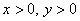 .
Из второго уравнения находим .
Из второго уравнения находим 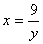 и подставляем в первое: и подставляем в первое: 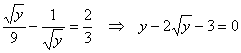 .
Делаем замену переменной: .
Делаем замену переменной: 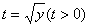 . Получаем квадратное уравнение относительно t:
. Получаем квадратное уравнение относительно t: 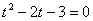 . Получим корни:
. Получим корни: 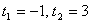 .
Но согласно замене .
Но согласно замене 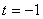 не подходит.
Поэтому
не подходит.
Поэтому 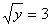 . Отсюда . Отсюда 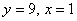 .
Ответ: (1; 9).
Задача 16.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. первый
выходит из А на 6 часов позже, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть .
Ответ: (1; 9).
Задача 16.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. первый
выходит из А на 6 часов позже, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть 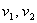 (км/ч) –
скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение
пешеходов. (км/ч) –
скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение
пешеходов.
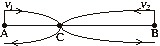
| Т.к. участок ВС первый прошел за 8 часов, то 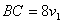 . Второй прошел расстояние СА за 9 часов, поэтому . Второй прошел расстояние СА за 9 часов, поэтому 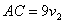 . . |
Страницы: 1, 2, 3, 4
|
|
|
|
|

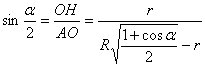 , значит, ответ:
, значит, ответ: 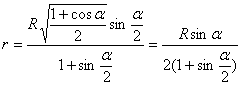 .
Задача 23.
Решить уравнение:
.
Задача 23.
Решить уравнение: 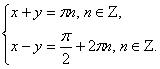 Решая последнюю систему, получаем
Ответ:
Решая последнюю систему, получаем
Ответ: 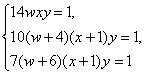 надо найти w, x.
Приравняв левые части первого и второго, а также первого и третьего уравнений
и упростив, получим систему
надо найти w, x.
Приравняв левые части первого и второго, а также первого и третьего уравнений
и упростив, получим систему
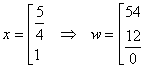 . Следовательно, второе значение х не подходит. Поэтому получили
Ответ: всего было 54 рабочих; они работали 1,25 часов в день.
3.2. Ответы (протоколы верных решений)
Задача 1.
Решить неравенство:
. Следовательно, второе значение х не подходит. Поэтому получили
Ответ: всего было 54 рабочих; они работали 1,25 часов в день.
3.2. Ответы (протоколы верных решений)
Задача 1.
Решить неравенство: 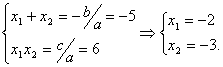 График функции
График функции 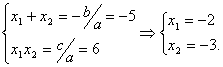 График функции
График функции 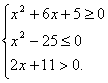 Решение:
Решаем каждое из неравенств системы в отдельности:
1.
Решение:
Решаем каждое из неравенств системы в отдельности:
1. 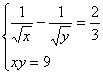 .
Решение:
ОДЗ:
.
Решение:
ОДЗ: 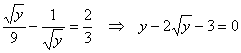 .
Делаем замену переменной:
.
Делаем замену переменной: