|
|
|
|
Диплом: Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Из условия задачи имеем: 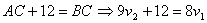 .
Выразим теперь время, затраченное пешеходами от начала движения до их встречи: .
Выразим теперь время, затраченное пешеходами от начала движения до их встречи: 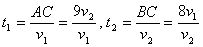 .
Т.к. первый вышел на 6 часов раньше, то: .
Т.к. первый вышел на 6 часов раньше, то: 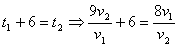 .
Сделаем замену: .
Сделаем замену: 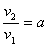 и
решим уравнение: и
решим уравнение: 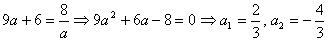 .
Но a – это отношение скоростей, а значит больше нуля. Получили систему: .
Но a – это отношение скоростей, а значит больше нуля. Получили систему:
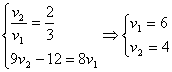 . Значит, . Значит, 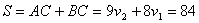 .
Ответ: .
Ответ: 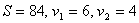 .
Задача 17.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. первый
выходит из А на 6 часов позже, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть .
Задача 17.
Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. первый
выходит из А на 6 часов позже, чем второй из В, и при встрече в пункте С
оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи
путь с той же скоростью, первый приходит в В через 8 часов после встречи, а
второй в А – через 9 часов. Определить расстояние АВ и скорость обоих
пешеходов.
Решение:
Пусть 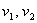 (км/ч) –
скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение
пешеходов. (км/ч) –
скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение
пешеходов.
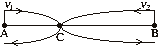
| Т.к. участок ВС первый прошел за 8 часов, то 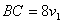 . Второй прошел расстояние СА за 9 часов, поэтому . Второй прошел расстояние СА за 9 часов, поэтому 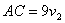 . . |
Из условия задачи имеем: 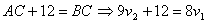 .
Выразим теперь время, затраченное пешеходами от начала движения до их встречи: .
Выразим теперь время, затраченное пешеходами от начала движения до их встречи: 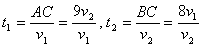 .
Т.к. первый вышел на 6 часов раньше, то: .
Т.к. первый вышел на 6 часов раньше, то: 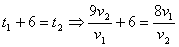 .
Сделаем замену: .
Сделаем замену: 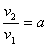 и
решим уравнение: и
решим уравнение: 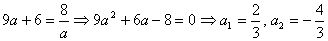 .
Но a – это отношение скоростей, а значит больше нуля. Получили систему: .
Но a – это отношение скоростей, а значит больше нуля. Получили систему:
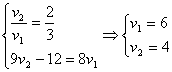 . Значит, . Значит, 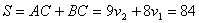 .
Ответ: .
Ответ: 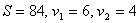 .
Задача 18.
Решить задачу: Две трубы, работая одновременно, наполняют бассейн за 12
часов. Одна первая труба наполняет бассейн на 10 часов медленнее, чем одна
вторая. За сколько часов наполняет бассейн одна вторая труба?
Решение:
Положим объем бассейна = 1. Пусть .
Задача 18.
Решить задачу: Две трубы, работая одновременно, наполняют бассейн за 12
часов. Одна первая труба наполняет бассейн на 10 часов медленнее, чем одна
вторая. За сколько часов наполняет бассейн одна вторая труба?
Решение:
Положим объем бассейна = 1. Пусть 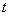 (ч) – время наполнения бассейна одной второй трубой. Тогда одна первая труба
наполнит бассейн за
(ч) – время наполнения бассейна одной второй трубой. Тогда одна первая труба
наполнит бассейн за 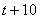 часов. Находим производительность этих труб:
часов. Находим производительность этих труб: 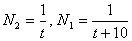 . За 12 часов совместной работы с общей производительностью
. За 12 часов совместной работы с общей производительностью 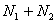 заполняется весь бассейн:
заполняется весь бассейн: 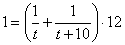 . Решаем полученное уравнение:
. Решаем полученное уравнение: 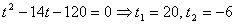 .
Ответ:
.
Ответ: 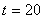 .
Задача 19.
Решить задачу: В ателье поступило по одному куску черной, зеленой и синей
ткани. Хотя зеленой ткани было на 9 м меньше, чем черной, и на 6 м больше,
чем синей, стоимость кусков была одинаковой. Сколько метров ткани было в
каждом куске, если известно, что стоимость 4.5 м черной ткани = общей
стоимости 3 м зеленой и 50 см синей?
Решение:
Пусть .
Задача 19.
Решить задачу: В ателье поступило по одному куску черной, зеленой и синей
ткани. Хотя зеленой ткани было на 9 м меньше, чем черной, и на 6 м больше,
чем синей, стоимость кусков была одинаковой. Сколько метров ткани было в
каждом куске, если известно, что стоимость 4.5 м черной ткани = общей
стоимости 3 м зеленой и 50 см синей?
Решение:
Пусть 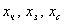 -количество черной, зеленой и синей ткани соответственно.
Известно: -количество черной, зеленой и синей ткани соответственно.
Известно: 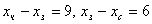 .
Используем формулу: .
Используем формулу: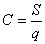 ,
где ,
где 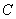 - цена ткани,
S – стоимость куска, q – количество ткани.
Пусть S = 1. Получим - цена ткани,
S – стоимость куска, q – количество ткани.
Пусть S = 1. Получим 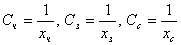 - цены тканей. Составим уравнение, связывающее эти стоимости:
- цены тканей. Составим уравнение, связывающее эти стоимости: 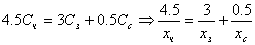 .
Выразим
.
Выразим 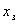 и и 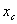 через через 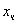 : : 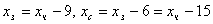 .
Подставляем в последнее уравнение: .
Подставляем в последнее уравнение: 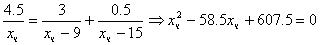 , причем , причем 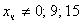 . .
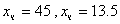 . Получили
1. . Получили
1. 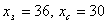 .
2. .
2. 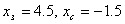 - невозможно.
Ответ: 45м, 36м, 30м.
Задача 20.
Решить уравнение: - невозможно.
Ответ: 45м, 36м, 30м.
Задача 20.
Решить уравнение: 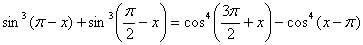 .
Решение:
По формулам приведения приведем все функции к одному аргументу: .
Решение:
По формулам приведения приведем все функции к одному аргументу: 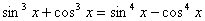 . По формулам сокращенного умножения разложим на множители:
. По формулам сокращенного умножения разложим на множители:
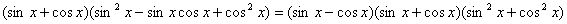 . По основному тригонометрическому тождеству
. По основному тригонометрическому тождеству 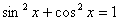 , поэтому остается уравнение: , поэтому остается уравнение:
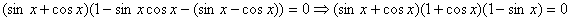 .
Рассмотрим 3 случая:
1.
.
Рассмотрим 3 случая:
1. 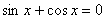 .
Разделим на .
Разделим на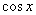 , причем , причем 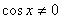 . Тогда имеем уравнение: tg x = - 1. Следовательно,
. Тогда имеем уравнение: tg x = - 1. Следовательно, 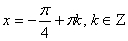 .
2.
.
2. 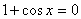 , cos x = -1. Следовательно, , cos x = -1. Следовательно, 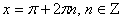 .
3. .
3. 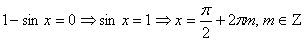 .
Получили ответ: .
Получили ответ: 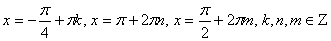 .
Задача 21.
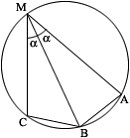
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1
см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.
Решение:
Отрезки .
Задача 21.
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1
см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.
Решение:
Отрезки 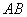 и и 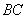 равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения
второе и получим:
равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения
второе и получим: 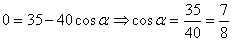 . Значит,
. Значит, 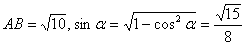 .
Треугольник .
Треугольник 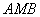 вписан
в окружность, следовательно, радиус данной окружности можно найти с помощью
теоремы синусов: вписан
в окружность, следовательно, радиус данной окружности можно найти с помощью
теоремы синусов: 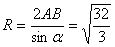 .
Ответ: .
Ответ: 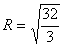 .
Задача 22.
Решить задачу: В сектор радиуса .
Задача 22.
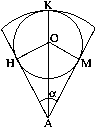
Решить задачу: В сектор радиуса 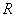 с центральным углом
с центральным углом 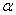 вписан круг. Найти его радиус.
Решение:
Т.к. центры окружностей и точки касания лежат на одной прямой, то
вписан круг. Найти его радиус.
Решение:
Т.к. центры окружностей и точки касания лежат на одной прямой, то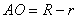 . Рассмотрим треугольник АОН (он прямоугольный, т.к. угол
. Рассмотрим треугольник АОН (он прямоугольный, т.к. угол 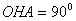 ): угол
): угол 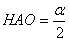 из
равенства треуг-ков АОН и АОМ (т.к. ОН=ОМ=r, АН=АМ как
отрезки касательных, проведенных из одной точки, сторона АО - общая). из
равенства треуг-ков АОН и АОМ (т.к. ОН=ОМ=r, АН=АМ как
отрезки касательных, проведенных из одной точки, сторона АО - общая). 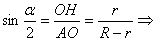 Ответ:
Ответ: 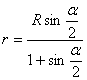 .
Задача 23.
Решить уравнение: .
Задача 23.
Решить уравнение: 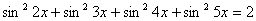 .
Решение:
ОДЗ: .
Решение:
ОДЗ: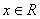 .
Применяя формулы понижения степени, приведем это уравнение к более простому
виду: .
Применяя формулы понижения степени, приведем это уравнение к более простому
виду:
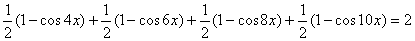 ,
, 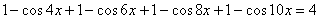 , ,
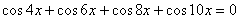 .
Отсюда, используя формулу преобразования суммы косинусов в произведение,
получаем: .
Отсюда, используя формулу преобразования суммы косинусов в произведение,
получаем: 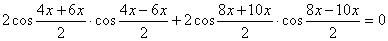 , ,
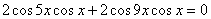 , ,
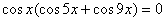 .
Рассмотрим 2 случая:
1. .
Рассмотрим 2 случая:
1. 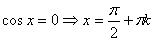 ;
2. ;
2. 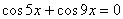 ,
следовательно, используя вновь формулу преобразования суммы косинусов в
произведение, имеем: ,
следовательно, используя вновь формулу преобразования суммы косинусов в
произведение, имеем:
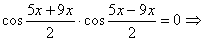 a)
a) 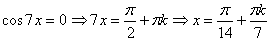 ;
b) ;
b) 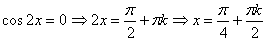 .
Таким образом, учитывая ОДЗ, получаем
Ответ: .
Таким образом, учитывая ОДЗ, получаем
Ответ: 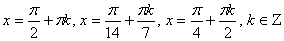 .
Задача 24.
Решить уравнение: .
Задача 24.
Решить уравнение: 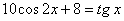 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 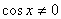 .
Введем новую переменную, положив t = tg x. Так как .
Введем новую переменную, положив t = tg x. Так как 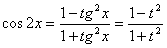 , то уравнение примет вид:
, то уравнение примет вид: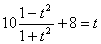 или
или 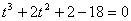 . Число 2
является корнем полученного уравнения, поэтому это уравнение можно
преобразовать следующим образом: . Число 2
является корнем полученного уравнения, поэтому это уравнение можно
преобразовать следующим образом: 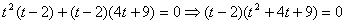 . Квадратный трехчлен во второй скобке не имеет действительных корней.
Следовательно, уравнение имеет только один корень. Найдем корни исходного
уравнения:
. Квадратный трехчлен во второй скобке не имеет действительных корней.
Следовательно, уравнение имеет только один корень. Найдем корни исходного
уравнения:
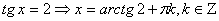 .
Дополнительный случай рассматривать не надо, так как .
Дополнительный случай рассматривать не надо, так как 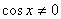 .
Ответ: .
Ответ: 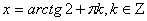 .
Задача 25.
Решить уравнение: .
Задача 25.
Решить уравнение: 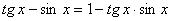 .
Решение:
ОДЗ: .
Решение:
ОДЗ: 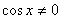 , т.е. , т.е. 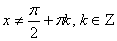 .
Преобразуем уравнение следующим образом: .
Преобразуем уравнение следующим образом:
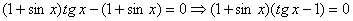 .
Рассмотрим 2 случая:
1. .
Рассмотрим 2 случая:
1. 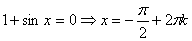 ; в этом
случае исходное уравнение решений не имеет, т.к. данные значения не входят в
ОДЗ;
2. ; в этом
случае исходное уравнение решений не имеет, т.к. данные значения не входят в
ОДЗ;
2. 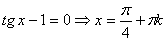 ; эти значения входят в ОДЗ уравнения.
Ответ: ; эти значения входят в ОДЗ уравнения.
Ответ: 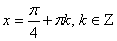 .
Задача 26.
Решить систему: .
Задача 26.
Решить систему: 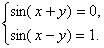 Решение:
Каждое из уравнений этой системы является простейшим, поэтому нетрудно
заметить, что
Решение:
Каждое из уравнений этой системы является простейшим, поэтому нетрудно
заметить, что
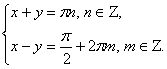 Решая последнюю систему, получаем
Ответ:
Решая последнюю систему, получаем
Ответ: 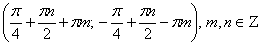 .
Задача 27.
Решить задачу: Основания трапеции 5 дм и 40 см. Найти длину отрезка,
соединяющего середины диагоналей.
Решение: .
Задача 27.
Решить задачу: Основания трапеции 5 дм и 40 см. Найти длину отрезка,
соединяющего середины диагоналей.
Решение:
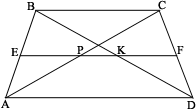
| Пусть ABCD – трапеция, точка Р – середина диагонали АС, точка К – середина диагонали BD. |
Нетрудно заметить, что точки Р и К лежат на средней линии EF
трапеции. Так как ЕК – средняя линия треугольника ABD, то 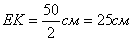 . Аналогично,
. Аналогично, 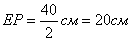 ,
поскольку является средней линией треугольника АВС. Следовательно, ,
поскольку является средней линией треугольника АВС. Следовательно, 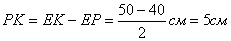 .
Ответ: 5 см.
Задача 28.
Решить задачу: Даны 2 стороны треугольника a, b и медиана
.
Ответ: 5 см.
Задача 28.
Решить задачу: Даны 2 стороны треугольника a, b и медиана 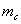 , проведенная к стороне c. Найти сторону с.
Решение:
, проведенная к стороне c. Найти сторону с.
Решение:
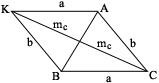
| Достроим треугольник АВС до параллелограмма АВСК. При этом 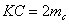 . По свойству параллелограмма сумма квадратов его диагоналей равна сумме квадратов его сторон. Поэтому из равенства . По свойству параллелограмма сумма квадратов его диагоналей равна сумме квадратов его сторон. Поэтому из равенства 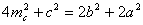 получаем получаем |
Ответ: 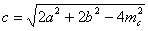 .
Задача 29.
Решить задачу: Даны 2 стороны треугольника a, b и медиана .
Задача 29.
Решить задачу: Даны 2 стороны треугольника a, b и медиана 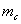 , проведенная к стороне c. Найти сторону с.
Решение:
, проведенная к стороне c. Найти сторону с.
Решение:
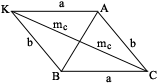
| Достроим треугольник АВС до параллелограмма АВСК. При этом 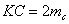 . По свойству параллелограмма сумма квадратов его диагоналей равна сумме квадратов его сторон. Поэтому из равенства . По свойству параллелограмма сумма квадратов его диагоналей равна сумме квадратов его сторон. Поэтому из равенства 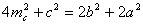 получаем получаем |
Ответ: 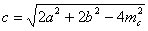 .
Задача 30.
Решить задачу: Несколько рабочих выполняют работу за 14 дней. Если бы их
было на 4 человека больше и каждый работал в день на 1 час больше, то та же
работа была бы сделана за 10 дней. Если бы их было еще на 6 человек больше и
каждый работал бы еще на 1 час в день больше, то эта работа была бы сделана
за 7 дней. Сколько было рабочих, и сколько часов в день они работали?
Решение:
Пусть w - число рабочих, х – число часов их работы в день.
Пусть вся работа равна единице, а у – производительность (в час)
каждого рабочего.
Тогда один рабочий за х часов (т.е. в день) выполняет ху единиц
работы, а w рабочих за 14 дней выполнят 14wxy единиц работы.
Согласно условию 14wxy = 1.
Аналогично, если рабочих стало w + 4, и они работают каждый день х + 1 час, то
10(w + 4)(x + 1)y = 1.
Для случая, когда рабочих еще на 6 человек больше (т.е. w + 10), и они
работают еще на час дольше (т.е. х + 2 часа) каждый день, получаем
уравнение 7(w + 10)(x + 2)y = 1.
Из системы .
Задача 30.
Решить задачу: Несколько рабочих выполняют работу за 14 дней. Если бы их
было на 4 человека больше и каждый работал в день на 1 час больше, то та же
работа была бы сделана за 10 дней. Если бы их было еще на 6 человек больше и
каждый работал бы еще на 1 час в день больше, то эта работа была бы сделана
за 7 дней. Сколько было рабочих, и сколько часов в день они работали?
Решение:
Пусть w - число рабочих, х – число часов их работы в день.
Пусть вся работа равна единице, а у – производительность (в час)
каждого рабочего.
Тогда один рабочий за х часов (т.е. в день) выполняет ху единиц
работы, а w рабочих за 14 дней выполнят 14wxy единиц работы.
Согласно условию 14wxy = 1.
Аналогично, если рабочих стало w + 4, и они работают каждый день х + 1 час, то
10(w + 4)(x + 1)y = 1.
Для случая, когда рабочих еще на 6 человек больше (т.е. w + 10), и они
работают еще на час дольше (т.е. х + 2 часа) каждый день, получаем
уравнение 7(w + 10)(x + 2)y = 1.
Из системы
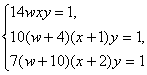 надо найти w, x.
Приравняв правые части первого и второго, а также первого и третьего
уравнений и упростив, получим систему
надо найти w, x.
Приравняв правые части первого и второго, а также первого и третьего
уравнений и упростив, получим систему
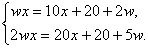 Если вычесть из второго уравнения удвоенное первое, то х исчезнет, и
найдем, что w = 20. Отсюда легко получается, что х = 6.
Ответ: всего было 20 рабочих; они работали 6 часов в день.
3.3. Ошибки, допущенные в задачах
1. Теорема Виета применена неверно: коэффициенты p и q взяты для
неприведенного уравнения и с противоположными знаками.
2. Неправильно построен график.
3. Потеря корней путем сокращения.
4. Концы интервалов включены в ответ, хотя они не удовлетворяют данному
неравенству.
5. Не сменили знак неравенства при умножении обеих его частей на
отрицательное число.
6. Для получения решения системы неравенств взято не пересечение, а
объединение решений каждого отдельного неравенства.
7. Не указано ОДЗ: знаменатель не должен быть равен нулю.
8. Нерациональность в приведении к общему знаменателю.
9. Нигде не учтены условия, при которых были сняты знаки модуля.
10. Рассмотрены не все случаи, возникающие при снятии знаков модуля.
11. Во втором случае неправильно снят знак модуля.
12. Не указано ОДЗ: арифметический квадратный корень определен только для
неотрицательных чисел.
13. При возведении в квадрат обеих частей уравнения не учтены их знаки.
14. Не учтено, что корень из квадрата числа равен модулю этого числа.
15. Сделана неэквивалентная замена переменной.
16. Неправильно понят смысл слова “раньше”.
17.
17.1. Неправильно составлено уравнение, связывающее величины АС и ВС;
17.2. Не учтено, что скорость не может быть отрицательной.
18. Неправильно применена формула производительности через объем работы и время.
19. Выполнены преобразования с величинами в разных единицах измерения.
20. Неправильно применены формулы приведения.
21.
21.1. Неправильно применена теорема косинусов;
21.2. Неправильно применено основное тригонометрическое тождество;
21.3. Неправильно применена теорема синусов.
22. Неправильно сделан чертеж.
23. В формуле преобразования суммы косинусов в произведение во втором
множителе cos заменили на sin.
24. Потеря корня путем сокращения.
25. Не указано ОДЗ уравнения.
26. Неправильно произведен отбор корней (в каждом из уравнений системы должна
быть своя буква, а не одна n).
27. Выполнены преобразования с разными единицами измерения.
28. Неправильно применено свойство параллелограмма.
29. Перепутали формулы для медианы и биссектрисы.
30. Получили систему уравнений, не соответствующую условиям задачи.
ПРИЛОЖЕНИЕ
Программа “Генератор неправильных решений”
“Генератор неправильных решений” (Wrong Solution Generator v.3.3) по
заданному линейному или квадратному уравнению выдает протокол решения с
допущенными в нем ошибками (или без них). Пользователю необходимо найти и
отметить допущенные в решении ошибки.
Программа написана с использованием Microsoft Visual C++ 6.0/MFC 4.2.
Описание интерфейса программы:
Если вычесть из второго уравнения удвоенное первое, то х исчезнет, и
найдем, что w = 20. Отсюда легко получается, что х = 6.
Ответ: всего было 20 рабочих; они работали 6 часов в день.
3.3. Ошибки, допущенные в задачах
1. Теорема Виета применена неверно: коэффициенты p и q взяты для
неприведенного уравнения и с противоположными знаками.
2. Неправильно построен график.
3. Потеря корней путем сокращения.
4. Концы интервалов включены в ответ, хотя они не удовлетворяют данному
неравенству.
5. Не сменили знак неравенства при умножении обеих его частей на
отрицательное число.
6. Для получения решения системы неравенств взято не пересечение, а
объединение решений каждого отдельного неравенства.
7. Не указано ОДЗ: знаменатель не должен быть равен нулю.
8. Нерациональность в приведении к общему знаменателю.
9. Нигде не учтены условия, при которых были сняты знаки модуля.
10. Рассмотрены не все случаи, возникающие при снятии знаков модуля.
11. Во втором случае неправильно снят знак модуля.
12. Не указано ОДЗ: арифметический квадратный корень определен только для
неотрицательных чисел.
13. При возведении в квадрат обеих частей уравнения не учтены их знаки.
14. Не учтено, что корень из квадрата числа равен модулю этого числа.
15. Сделана неэквивалентная замена переменной.
16. Неправильно понят смысл слова “раньше”.
17.
17.1. Неправильно составлено уравнение, связывающее величины АС и ВС;
17.2. Не учтено, что скорость не может быть отрицательной.
18. Неправильно применена формула производительности через объем работы и время.
19. Выполнены преобразования с величинами в разных единицах измерения.
20. Неправильно применены формулы приведения.
21.
21.1. Неправильно применена теорема косинусов;
21.2. Неправильно применено основное тригонометрическое тождество;
21.3. Неправильно применена теорема синусов.
22. Неправильно сделан чертеж.
23. В формуле преобразования суммы косинусов в произведение во втором
множителе cos заменили на sin.
24. Потеря корня путем сокращения.
25. Не указано ОДЗ уравнения.
26. Неправильно произведен отбор корней (в каждом из уравнений системы должна
быть своя буква, а не одна n).
27. Выполнены преобразования с разными единицами измерения.
28. Неправильно применено свойство параллелограмма.
29. Перепутали формулы для медианы и биссектрисы.
30. Получили систему уравнений, не соответствующую условиям задачи.
ПРИЛОЖЕНИЕ
Программа “Генератор неправильных решений”
“Генератор неправильных решений” (Wrong Solution Generator v.3.3) по
заданному линейному или квадратному уравнению выдает протокол решения с
допущенными в нем ошибками (или без них). Пользователю необходимо найти и
отметить допущенные в решении ошибки.
Программа написана с использованием Microsoft Visual C++ 6.0/MFC 4.2.
Описание интерфейса программы:
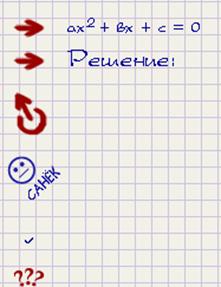
| Сменить уравнение. Сгенерировать другое решение. Проверить правильность ответа. Информация о создателях. Таким образом отмечается ошибка. Выбрать случайные коэффициенты уравнения. |
Описание классов:
1. Класс “Задача”:
class CTask
{
public:
int nPosibleErr; // число возможных ошибок
long m_a; //
long m_b; // коэффициенты уравнения
long m_c; //
BOOL m_arErrors[8]; // массив ошибок
CTask(); // конструктор
virtual ~CTask(); // деструктор
virtual void Draw(CDC *pDC, CRect *rect);
// отображает уравнение
virtual void InitErrors()=0; // инициализирует ошибки
virtual void DrawStep(int Step, CDC *pDC, CRect *pRect)=0;
// отображает протокол решения
virtual void DrawErrors(CDC *pDC, CRect *pRect)=0;
// отображает варианты возможных ошибок
};
2. Класс “Линейное уравнение”:
class CLinTask : public CTask
{
public:
CLinTask(); // конструктор
virtual ~CLinTask(); // деструктор
void InitErrors(); // инициализирует ошибки
void Draw(CDC *pDC, CRect *rect); // отображает уравнение
void DrawStep(int Step, CDC *pDC, CRect *pRect);
// отображает протокол решения
void DrawErrors(CDC *pDC, CRect *pRect);
// отображает варианты возможных ошибок
void SetError1(); // устанавливаются конкретные ошибки
void SetError2(); // на каждом шаге решения
};
3. Класс “Квадратное уравнение”:
class CEqTask : public CTask
{
public:
long m_d; // дискриминант
double m_x1, m_x2; // корни уравнения
public:
CRect m_rectError5; //
CRect m_rectError6; // области вывода картинок
CRect m_rectError7; //
CRect m_rectError8; //
CEqTask();// конструктор
virtual ~CEqTask();// деструктор
void Draw(CDC *pDC, CRect *rect); // отображает уравнения
void DrawErrors(CDC *pDC, CRect *pRect);
// отображает варианты возможных ошибок
void InitErrors(); // инициализирует ошибки
void DoStep(int nStep); // выполняет очередной шаг решения
void DrawStep(int Step, CDC *pDC, CRect *pRect);
// отображает протокол решения
private:
void Extract(long &before, long &after); // извлечение корня
void SetError1(); // устанавливаются конкретные ошибки
void SetError2(); // на каждом шаге решения
};
Описание модулей программы:
1. Модуль ввода данных (класс CInputDialog, файлы InputDialog.h,
InputDialog.сpp) – при запуске программы или при нажатии кнопки “Сменить
уравнение” появляется окно диалога с пользователем. Модуль отвечает за
изменение данных объекта “Задача”.
2. Модуль оценки ответа (класс CCheckResultDialog, файлы CheckResultDialog.h,
CheckResultDialog.cpp) – при нажатии кнопки “Проверить правильность ответа”
появляется диалог оценки ответа. Модуль проверяет, все ли допущенные ошибки
отмечены и сообщает, мало или много отмечено ошибок, верно или неверно
отмечены ошибки.
3. Основной модуль (классы CTask, CLinTask, CEqTask, Cwsg3Dlg, файлы Task.h,
Task.cpp, LinTask.h, LinTask.cpp, EqTask.h, EqTask.cpp, wsg3Dlg.h,
wsg3Dlg.cpp) – отвечает за решение и отображение задачи, а также связывает
между собой все остальные модули.
Листинги файлов не приведены по причине их большого объема, но при желании их
можно посмотреть на дискете.
ЛИТЕРАТУРА
1. Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для
поступающих в вузы. - М.: Наука, 1976. - 640 с.
2. Сборник конкурсных задач по математике для поступающих во втузы: Учебное
пособие / Под ред. М.И. Сканави. - М.: Высшая школа, 1980. - 541 с. (или
более поздние издания).
3. Лурье М.В., Александров Б.И. Пособие по геометрии. - М.: Изд-во МГУ, 1984.
- 256 с.
4. Мельников И.И., Сергеев И.Н. Как решать задачи по математике на
вступительных экзаменах. - Изд. 2-е, исправл. - М.: МП Азбука, 1994. - 352с.
5. Вавилов В.В., Мельников И.И. Олехник С.Н., Пасиченко П.И. Задачи по
математике. Уравнения и неравенства: Справочное пособие. - М.: Наука, 1987. -
240 с.
6. Вавилов В.В., Мельников И.И. Олехник С.Н., Пасиченко П.И. Задачи по
математике. Алгебра: Справочное пособие. - М.: Наука, 1988. - 432 с.
7. Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Конкурсные задачи по
математике: Справочное пособие. - М.: Наука, 1992. - 480 с.
8. Потапов М.К., Александров В.В., Пасиченко П.И. Алгебра и анализ
элементарных функций. - М.: Наука, 1980. - 560 с.
9. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. - Киев:
РИА "Текст": МП "ОКО", 1992. - 290 с.
10. Говоров В.М., Дыбов П.Т., Мирошин Н.В., Смирнов С.Ф. Сборник конкурсных
задач по математике (с методическими указаниями и решениями). - М.: Наука,
1983. - 384 с. (или более поздние издания).
11. Пособие по математике для поступающих в вузы / Под. ред. Г.Н. Яковлева .
- М.: Наука, 1981. - 608 с.
12. Черкасов О.Ю., Якушев А.Г. Математика на вступительных экзаменах
("Скорая помощь" абитуриентам).-М.: "Московский лицей", 1995.-352 с.
13. Вирченко Н.А., Ляшко И.И., Швецов К.И. Графики функций: Справочник. -
Киев: Наукова думка, 1979. - 320 с.
14. Звавич Л.И., Шляпочник Л.Я. Задачи письменного экзамена по математике за
курс средней школы: Условия и решения. Вып. 3 - М.: Школа-Пресс, 1994. - 192
с.
15. Далингер В.А., Типичные ошибки по математике на вступительных экзаменах
и как их не допускать. Обл. ин-т усоверш. учителей, Омск-1991.
16. Дудницын В.П., Смирнова В.К., Содержание и анализ письменных
экзаменационных работ по алгебре и началам анализа за курс средней школы.
Львов, «Квантор» - 1991.
17. Агалаков С.А., Пособие по математике для поступающих в ОмГУ. Омск – 1997.
18. Павлович В.С., Анализ ошибок абитуриентов по математике. Киев, «Вища
школа» - 1985.
Страницы: 1, 2, 3, 4
|
|
|
|
|

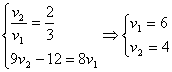 . Значит,
. Значит, 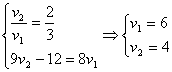 . Значит,
. Значит, 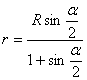 .
Задача 23.
Решить уравнение:
.
Задача 23.
Решить уравнение: 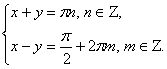 Решая последнюю систему, получаем
Ответ:
Решая последнюю систему, получаем
Ответ: 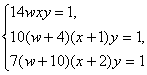 надо найти w, x.
Приравняв правые части первого и второго, а также первого и третьего
уравнений и упростив, получим систему
надо найти w, x.
Приравняв правые части первого и второго, а также первого и третьего
уравнений и упростив, получим систему