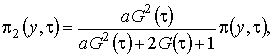|
РУБРИКИ |
Диплом: Асимптотические методы исследования нестационарных режимов в сетях случайного доступа |
РЕКОМЕНДУЕМ |
||
|
Диплом: Асимптотические методы исследования нестационарных режимов в сетях случайного доступаТеперь приведем подобные слагаемые, учтем равенства (1.6), и получим неоднородную линейную систему алгебраических уравнений для нахождения неизвестных функций такого вида , (1.10) Нетрудно заметить, что ранг матрицы однородной системы алгебраических уравнений, соответствующей (1.10) равен двум. Следовательно, для того, чтобы система была разрешима, необходимо, чтобы ранг расширенной матрицы этой системы был равен двум, т.е. чтобы выполнялось следующее равенство С учетом того, что равенство (1.11) принимает вид Равенство нулю производной противоречит смыслу задачи, следовательно , т. е. пропускная способность исследуемой сети связи равна асимптотической вероятности того, что обслуживающий прибор «обслуживает», на рис. 1.5 продемонстрирован этот результат.
Рис. 1.5 Таким образом, мы выяснили, что система (1.10) разрешима. Ее решение можно записать так , функция, (1.13) . Перейдем к третьему этапу. 3 этап. Запишем уравнения системы (1.2) с точностью до , (1.14) Как и на втором этапе в полученные уравнения подставим в форме (1.7), заменим разностью на G и не учтем слагаемые, имеющие порядок выше , получим (1.15) Просуммировав все уравнения системы (1.15), получим равенство для нахождения (1.16) Подставляя выражения для , найденные на втором этапе, для получим уравнение Фоккера-Планка где Решим уравнение (1.17) с помощью преобразования Лапласа по x. Левую и правую части уравнения умножим на и проинтегрируем. С учетом обозначения и свойств этой функции уравнение (1.17) приобретет вид (1.18) Таким образом, мы перешли от уравнения Фоккера-Планка с постоянными коэффициентами к обыкновенному дифференциальному уравнению, решение которого с точностью до неизвестных , записывается следующим образом (1.19) Для того чтобы получить окончательное решение уравнения (1.17) нужно провести дополнительное исследование, которое бы показало поведение исследуемого процесса в окрестности нуля. Используя асимптотику , это не удается сделать. Предположим, что сеть связи функционирует в стационарном режиме, тогда (1.17) перепишется в виде Следовательно, в стационарном режиме асимптотическое распределение вероятностей нормированного числа заявок в источнике повторных вызовов подчиняется экспоненциальному закону с параметром и 2. Исследование неоднородной нестационарной сети случайного доступа с динамическим протоколом в условиях перегрузки
Рассмотрим сеть связи, описанную в разделе 1, в которой интенсивность входящего потока зависит от времени и равна , где Т – некоторый интервал времени, в течение которого функционирует сеть связи. Структура сети изображена на рис. 2.1.
Рис. 2.1 – Модель системы массового обслуживания В нестационарном режиме распределение удовлетворяют системе дифференциально-разностных уравнений вида (2.1) где Замечание: система уравнений (2.1) получена аналогично системе уравнений (1.1). Вероятности переходов для состояний системы совпадают с точностью до замены Систему (2.1) будем решать в условиях перегрузки, то есть при Первое приближение В системе уравнений (2.1) произведем замену переменных: . В результате такой замены производится переход от дискретной переменной к непрерывной переменной , от t перешли к , причем . После замены производная равна . Тогда уравнения (2.1) перепишем (2.2) Решим систему уравнений (2.2) в два этапа. 1 этап. Считая Выразим где асимптотическая плотность распределения нормированного числа заявок в источнике повторных вызовов. Обозначим ( асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Заметим, что из системы (2.3) следуют равенства связывающие и Найдем вид функции 2 этап. В системе дифференциальных уравнений (2.2) все функции с аргументом разложим в ряд по приращению аргумента , ограничиваясь слагаемыми порядка , получим (2.7) Просуммируем левые и правые части уравнений системы (2.7) и получим равенство . (2.8) С учетом того, что равенство (2.8) принимает вид Уравнение (2.9) является однородным линейным уравнением с частными производными первого порядка. Для того чтобы его решить составим уравнение его решение Общее решение уравнения (2.9) имеет вид где дифференцируемая функция, аналитическое выражение которой найдем из начальных условий. Пусть распределение в начальный момент времени где плотность распределения. Тогда следовательно Возьмем в качестве начальной плотности распределения , где дельта-функция Дирака, а , источнике повторных вызовов в начальный момент времени. Таким образом То есть мы получили, что Из приведенных рассуждений вытекает еще одно важное следствие, а именно , тогда (отрицательная функция противоречит смыслу задачи). В нашем случае совпадает с пропускной способностью системы. Перейдем ко второму приближению, в котором будем искать распределение отклонения от асимптотического среднего. Второе приближение В исходной системе уравнений (2.1) сделаем замену переменных Заметим, что в новых обозначениях производная по времени . С учетом этого система (2.1) примет вид (2.11) Решение системы уравнений (2.11) аналогично решению системы (2.2), но проводится в три этапа. 1 этап. В системе дифференциальных уравнений (2.13) сделаем предельный переход при и предположим, что , получим Решим эту систему аналогично тому, как решили систему уравнений (2.3). Введем функцию через нее |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2010 |
|
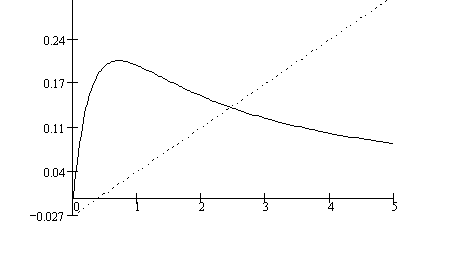
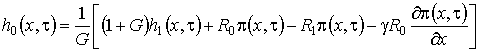
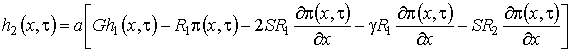
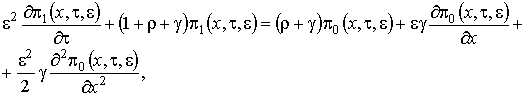
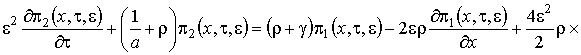
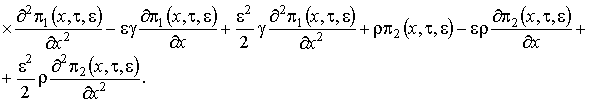
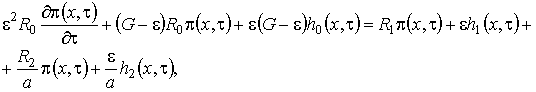
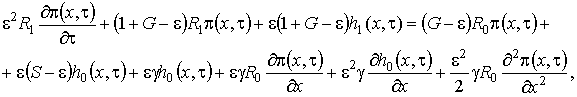
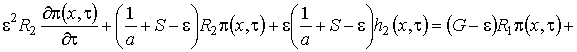
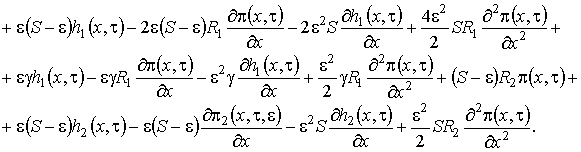
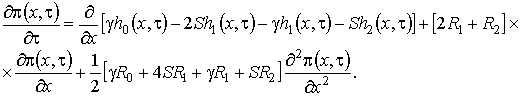
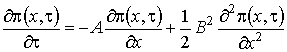 , (1.17)
, (1.17)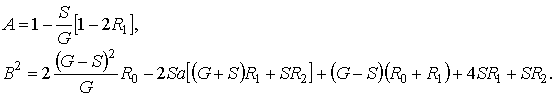
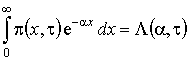
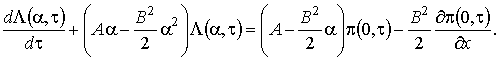
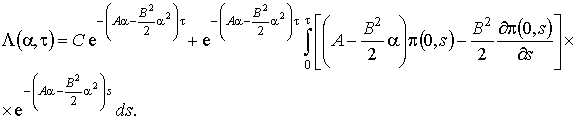
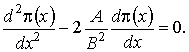 (1.20)
(1.20)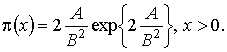 (1.21)
(1.21)

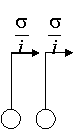
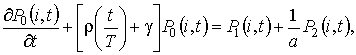
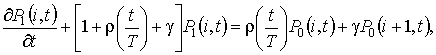
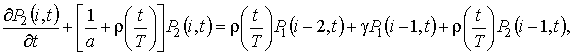
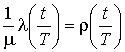 ,
, 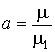 ,
, 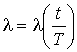 .
.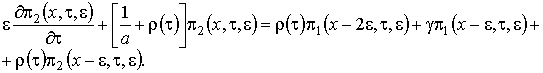
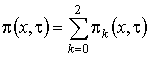 и получим
и получим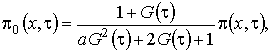
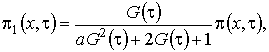 (2.4)
(2.4)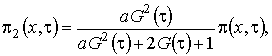
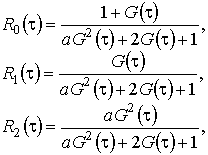 (2.5)
(2.5)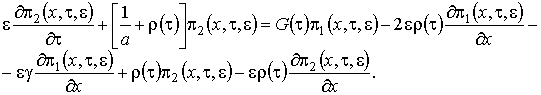
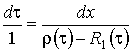 ,
, 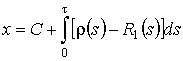 , тогда
, тогда 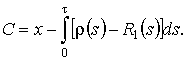
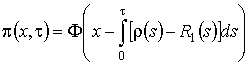 , (2.10)
, (2.10) .
.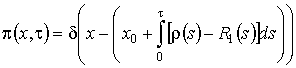 , из свойств функции Дирака следует, что
, из свойств функции Дирака следует, что 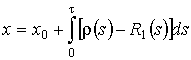 .
.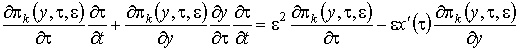
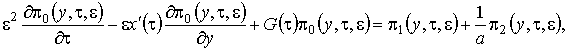
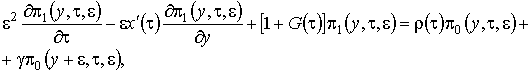
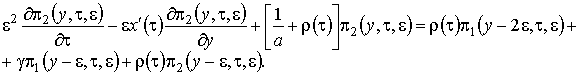
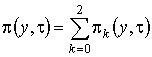 и выразим
и выразим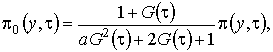
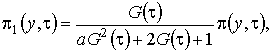 (2.13)
(2.13)