|
РУБРИКИ |
Диплом: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле |
РЕКОМЕНДУЕМ |
||
|
Диплом: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле/td> |
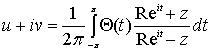 , (
, (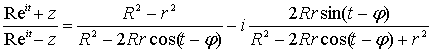 часть даст нам интеграл Пуассона для
часть даст нам интеграл Пуассона для 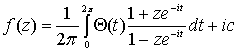 , (20)
где
, (20)
где 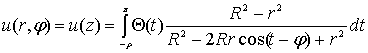 , (21)
где
, (21)
где
|
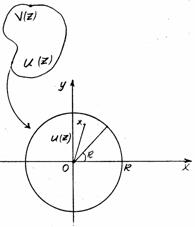
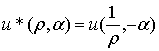 , гармоническую внутри круга радиуса
, гармоническую внутри круга радиуса 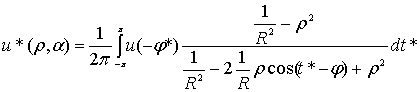 .
Если в этом равенстве подставить вместо
.
Если в этом равенстве подставить вместо 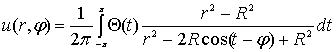 , (24)
решающую поставленную задачу. Она отличается от (1) только тем, что в ней
, (24)
решающую поставленную задачу. Она отличается от (1) только тем, что в ней
|
|
|
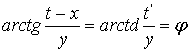 ,
, 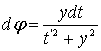 и окончательно имеем:
и окончательно имеем:
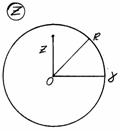
Пусть в плоскости комплексного переменного 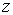 дано круговое кольцо
дано круговое кольцо 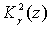 , ограниченное окружностями
, ограниченное окружностями
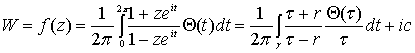 , (
, (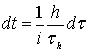 ,
, 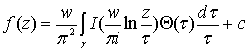 , (36)
где с – постоянная.
Формулу (36) можно назвать канонической, компактной и контурной интегральной
формулой Анри Вилля для кругового кольца.
б) Функции Вейерштрасса.
В виду важности трех функций Вейерштрасса
, (36)
где с – постоянная.
Формулу (36) можно назвать канонической, компактной и контурной интегральной
формулой Анри Вилля для кругового кольца.
б) Функции Вейерштрасса.
В виду важности трех функций Вейерштрасса 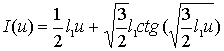 ,
,
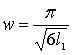 (39)
(39)
|
|
© 2010 |
|