|
РУБРИКИ |
Диплом: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле |
РЕКОМЕНДУЕМ |
||
|
Диплом: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле/td> |
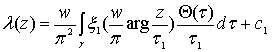 ,
,
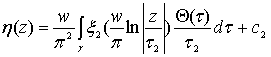 .
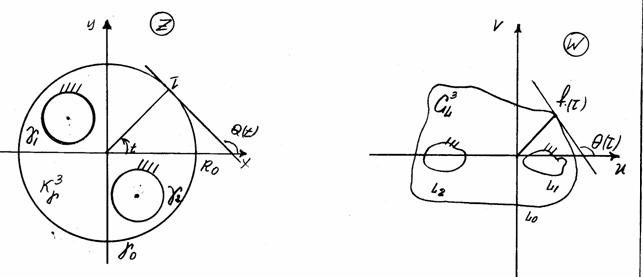
Таким образом, аналогичными примерами можно найти и для остальных рассмотренных
областей решения задачи Дирихле (
.
Таким образом, аналогичными примерами можно найти и для остальных рассмотренных
областей решения задачи Дирихле (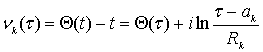 при
при 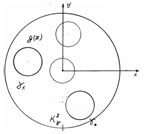 |
|
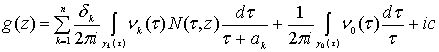 . (75)
Функция
. (75)
Функция 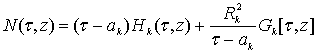 , (76)
, (76)
|
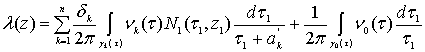 , (78)
, (78)
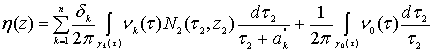 , (79)
где
, (79)
где 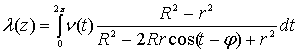 , (
, (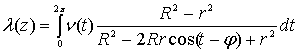 , (
, (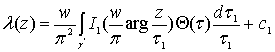 , (82)
, (82)
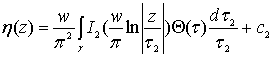 , (83)
где (74) и (75) – реальные и мнимые части компактной интегральной формулы
Вилля-Шварца для кругового кольца [2],
, (83)
где (74) и (75) – реальные и мнимые части компактной интегральной формулы
Вилля-Шварца для кругового кольца [2],
|
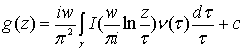 , (87)
, (87)
|
|
|
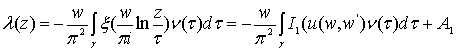 ,
,
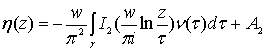 ,
где
,
где
|
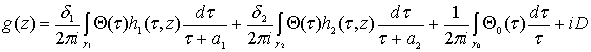 , (91)
где
, (91)
где 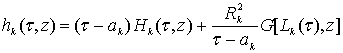 , где:
, где:
|
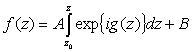 , (94)
(86) – есть формула Чизотти для конечных трехсвязных областей.
Итак, интегральная формула Чизотти для конечных трехсвязных областей имеет вид:
, (94)
(86) – есть формула Чизотти для конечных трехсвязных областей.
Итак, интегральная формула Чизотти для конечных трехсвязных областей имеет вид:
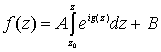 где А и В – постоянные, определяемые из нормировки функций:
где А и В – постоянные, определяемые из нормировки функций:
|
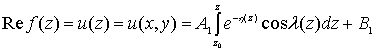
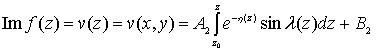 ,
где
,
где 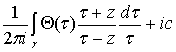 ,
,
|
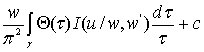 ,
, 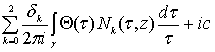 ,
,  , (97)
удовлетворяющие на границе
, (97)
удовлетворяющие на границе |
|
© 2010 |
|