|
|
|
|
Курсовая: Динамическое и линейное программирование
Курсовая: Динамическое и линейное программирование
Государственный университет управления
Институт заочного обучения
Специальность – менеджмент
Кафедра прикладной математики
КУРСОВОЙ ПРОЕКТ
по дисциплине: «Прикладная математика»
Выполнил студент 1-го курса
Группа № УП4-1-98/2
Студенческий билет №
Москва, 1999 г.
Содержание
1. Линейная производственная задача____________________________________________3
2. Двойственная задача_________________________________________________________7
3. Задача о «Расшивке узких мест производства»_________________________________9
4. Транспортная задача________________________________________________________12
5. Распределение капитальных вложений_________________________________________17
6. Динамическая задача управления запасами____________________________________21
7. Анализ доходности и риска финансовых операций______________________________26
8. Оптимальный портфель ценных бумаг__________________________________________28
1. Линейная производственная задача
Линейная производственная задача – это задача о рациональном использовании
имеющихся ресурсов, для решения которой применяют методы линейного
программирования. В общем виде задача может быть сформулирована следующим
образом:
Предположим, предприятие или цех может выпускать 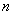 видов продукции, используя
видов продукции, используя 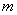 видов ресурсов. При этом известно количество каждого вида ресурса, расход
каждого вида ресурса на выпуск каждого вида продукции, прибыль, получаемая с
единицы выпущенной продукции. Требуется составить такой план производства
продукции, при котором прибыль, получаемая предприятием, была бы наибольшей.
Примем следующие обозначения:
видов ресурсов. При этом известно количество каждого вида ресурса, расход
каждого вида ресурса на выпуск каждого вида продукции, прибыль, получаемая с
единицы выпущенной продукции. Требуется составить такой план производства
продукции, при котором прибыль, получаемая предприятием, была бы наибольшей.
Примем следующие обозначения:
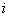
| Номер ресурса (i=1,2,.,m) | 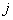
| Номер продукции (j=1,2,.,n) | 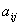
| Расход i-го ресурса на единицу j-ой продукции | 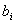
| Имеющееся количество i-го ресурса | 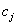
| Прибыль на единицу j-ой продукции | 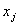
| Планируемое количество единиц j-ой продукции | 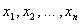
| Искомый план производства | | | |
Таким образом, математическая модель задачи состоит в том, чтобы найти
производственную программу 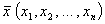 максимизирующую прибыль:
максимизирующую прибыль:
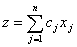 При этом, какова бы ни была производственная программа
При этом, какова бы ни была производственная программа 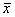 , ее компоненты должны удовлетворять условию, что суммарное использование
данного вида ресурса, при производстве всех видов продукции не должно превышать
имеющееся количество данного вида ресурса, т.е.
, ее компоненты должны удовлетворять условию, что суммарное использование
данного вида ресурса, при производстве всех видов продукции не должно превышать
имеющееся количество данного вида ресурса, т.е.
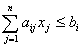 , где , где 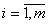 А так как компоненты программы – количество изделий, то они не могут быть
выражены отрицательными числами, следовательно добавляется еще одно условие:
А так как компоненты программы – количество изделий, то они не могут быть
выражены отрицательными числами, следовательно добавляется еще одно условие:
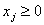 , где , где 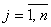 Предположим, что предприятие может выпускать четыре вида продукции (
Предположим, что предприятие может выпускать четыре вида продукции (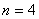 ), используя для этого три вида ресурсов (
), используя для этого три вида ресурсов (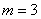 ). Известна технологическая матрица
). Известна технологическая матрица 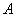 затрат любого ресурса на единицу каждой продукции, вектор
затрат любого ресурса на единицу каждой продукции, вектор 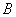 объемов ресурсов и вектор
объемов ресурсов и вектор 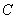 удельной прибыли:
удельной прибыли:
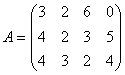 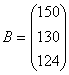 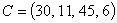 Тогда математическая модель задачи будет иметь вид:
Найти производственную программу
Тогда математическая модель задачи будет иметь вид:
Найти производственную программу 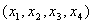 максимизирующую прибыль: максимизирующую прибыль:
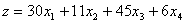
| (1.1) |
при ограничениях по ресурсам:
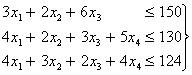
| (1.2) |
где по смыслу задачи: 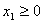 , , 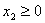 , , 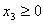 , , 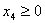 Таким образом, получили задачу на нахождение условного экстремума. Для ее
решения введем дополнительные неотрицательные неизвестные:
Тогда вместо системы неравенств (1.2), получим систему линейных
алгебраических уравнений:
Таким образом, получили задачу на нахождение условного экстремума. Для ее
решения введем дополнительные неотрицательные неизвестные:
Тогда вместо системы неравенств (1.2), получим систему линейных
алгебраических уравнений:
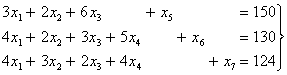
| (1.3) |
где среди всех решений, удовлетворяющих условию неотрицательности:
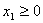 , , 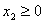 , , 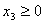 , , 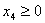 , , 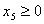 , , 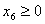 , , 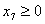 надо найти решение, при котором функция (1.1) примет наибольшее значение. Эту
задачу будем решать методом последовательного улучшения плана – симплексным
методом.
Воспользуемся тем, что правые части всех уравнений системы (1.3) неотрицательны,
а сама система имеет предпочитаемый вид – дополнительные переменные являются
базисными. Приравняв к нулю свободные переменные x1, x2,
x3, x4, получаем базисное неотрицательное решение:
надо найти решение, при котором функция (1.1) примет наибольшее значение. Эту
задачу будем решать методом последовательного улучшения плана – симплексным
методом.
Воспользуемся тем, что правые части всех уравнений системы (1.3) неотрицательны,
а сама система имеет предпочитаемый вид – дополнительные переменные являются
базисными. Приравняв к нулю свободные переменные x1, x2,
x3, x4, получаем базисное неотрицательное решение:
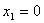 , , 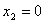 , , 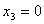 , , 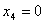 , , 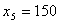 , , 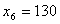 , , 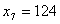 первые четыре компоненты которого представляют производственную программу
первые четыре компоненты которого представляют производственную программу 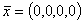 , по которой пока ничего не производится.
Из выражения (1.1) видно, что наиболее выгодно начинать производить продукцию
третьего вида, т.к. прибыль на единицу выпущенной продукции здесь наибольшая,
поэтому в системе (1.3) принимаем переменную x3 за разрешающую и
преобразуем эту систему к другому предпочитаемому виду. Для чего составляем
отношения правых частей уравнений к соответствующим положительным коэффициентам
при выбранной неизвестной и находим наибольшее значение x3, которое
она может принять при нулевых значениях других свободных неизвестных, сохранив
правые части уравнений неотрицательными, т.е.
, по которой пока ничего не производится.
Из выражения (1.1) видно, что наиболее выгодно начинать производить продукцию
третьего вида, т.к. прибыль на единицу выпущенной продукции здесь наибольшая,
поэтому в системе (1.3) принимаем переменную x3 за разрешающую и
преобразуем эту систему к другому предпочитаемому виду. Для чего составляем
отношения правых частей уравнений к соответствующим положительным коэффициентам
при выбранной неизвестной и находим наибольшее значение x3, которое
она может принять при нулевых значениях других свободных неизвестных, сохранив
правые части уравнений неотрицательными, т.е.
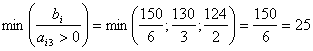 Оно соответствует первому уравнению в системе (1.3), и показывает какое
количество изделий третьего вида предприятие может изготовить с учетом объемов
сырья первого вида. Следовательно, в базис вводим неизвестную x3, а
исключаем от туда неизвестную x5. Тогда принимаем первое уравнение в
системе (1.3) за разрешающее, а разрешающим элементом будет a13=6.
Применив формулы исключения, переходим к новому предпочитаемому виду системы
с соответствующим базисным допустимым решением.
Полный процесс решения приведен в таблице 1, где в последней строке третьей
таблицы нет ни одного отрицательного относительного оценочного коэффициента
Оно соответствует первому уравнению в системе (1.3), и показывает какое
количество изделий третьего вида предприятие может изготовить с учетом объемов
сырья первого вида. Следовательно, в базис вводим неизвестную x3, а
исключаем от туда неизвестную x5. Тогда принимаем первое уравнение в
системе (1.3) за разрешающее, а разрешающим элементом будет a13=6.
Применив формулы исключения, переходим к новому предпочитаемому виду системы
с соответствующим базисным допустимым решением.
Полный процесс решения приведен в таблице 1, где в последней строке третьей
таблицы нет ни одного отрицательного относительного оценочного коэффициента
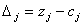 , где , где 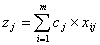 , где , где 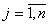 ,
т.е. выполняется критерий оптимальности для максимизируемой функции (1.1). ,
т.е. выполняется критерий оптимальности для максимизируемой функции (1.1).
Таблица 1 | | | C | Базис | H | 30 | 11 | 45 | 6 | 0 | 0 | 0 | Пояснения | | 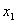
| | 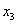
| 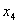
| 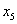
| 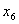
| 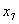
| | 0 | 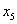
| 150 | 3 | 2 | 6 | 0 | 1 | 0 | 0 | 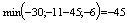
x3 – разрешающая переменная x3 ® в базис. 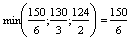
первая строка – разрешающая x5 ® из базиса. разрешающий элемент = 6 | | 0 | 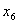
| 130 | 4 | 2 | 3 | 5 | 0 | 1 | 0 | | 0 | 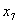
| 124 | 4 | 3 | 2 | 4 | 0 | 0 | 1 | | | 0 | | -30 | -11 | -45 | -6 | 0 | 0 | 0 | | 45 | 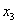
| 25 | 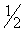
| 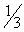
| 1 | 0 | 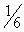
| 0 | 0 | 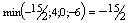
x1 – разрешающая переменная 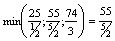
вторая строка – разрешающая разрешающий элемент = 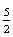 | | 0 | 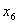
| 55 | 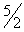
| 1 | 0 | 5 | 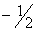
| 1 | 0 | | 0 | 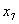
| 74 | 3 | 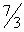
| 0 | 4 | 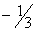
| 0 | 1 | | | 1125 | | 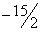
| 4 | 0 | -6 | 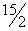
| 0 | 0 | |  45 45
| 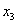
| 14 | 0 | 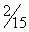
| 1 | -1 | 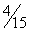
| 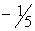
| 0 | Все 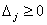 | | 30 | 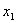
| 22 | 1 | 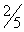
| 0 | 2 | 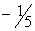
| 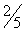
| 0 | | 0 | 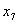
| 8 | 0 | 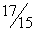
| 0 | -2 | 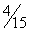
| 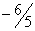
| 1 | | | 1290 | | 0 | 7 | 0 | 9 | 6 | 3 | 0 | | | | | | | | | | | | | |
При этом каждый элемент симплексной таблицы имеет определенный экономический
смысл. Например, во второй симплексной таблице:
В столбце 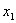 : : | 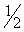
| Показывает, на сколько следует уменьшить изготовление изделия третьего вида, если запланирован выпуск одного изделия первого вида. | 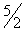 ; 3 ; 3
| Показывают, сколько потребуется сырья второго и третьего вида, при включении в план одного изделия первого вида. | | Т.е. при включении в план одного изделия первого вида, потребуется уменьшение выпуска продукции третьего вида на 0.5 единиц, а также потребуются дополнительные затраты 2.5 единиц сырья второго вида и 3 единицы сырья третьего вида, что приведет к увеличению прибыли предприятия на 7.5 денежных единиц. | В столбце 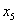 : : | 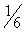 ; ;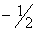 ; ;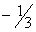
| Показывают, что увеличение объема сырья первого вида на единицу позволило бы увеличить выпуск продукции третьего вида на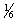 . . 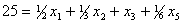
что одновременно потребовало бы 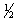 единицы сырья второго вида и единицы сырья второго вида и 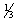 единицы сырья третьего вида. единицы сырья третьего вида. | | | |
Т.к. в последней строке третьей таблицы 1 нет ни одного отрицательного
относительного оценочного коэффициента, то производственная программа, при
которой получаемая предприятием прибыль имеет наибольшее значение, найдена,
т.к., например, коэффициент 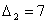 при переменной
при переменной 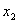 показывает, что если произвести одну единицу продукции второго вида, то прибыль
уменьшится на 7 денежных единиц.
Таким образом, получили производственную программу:
показывает, что если произвести одну единицу продукции второго вида, то прибыль
уменьшится на 7 денежных единиц.
Таким образом, получили производственную программу:
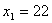 , , 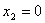 , , 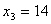 , , 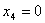 которая является оптимальной и обеспечивает предприятию наибольшую возможную
прибыль:
которая является оптимальной и обеспечивает предприятию наибольшую возможную
прибыль:
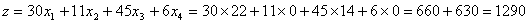 При этом первый и второй ресурсы будут использованы полностью, т.е. первый и
второй ресурсы образуют «узкие места производства»:
При этом первый и второй ресурсы будут использованы полностью, т.е. первый и
второй ресурсы образуют «узкие места производства»:
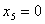 , , 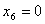 а третий ресурс будет иметь остаток:
а третий ресурс будет иметь остаток:
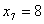 Помимо этого в третьей симплексной таблице получен обращенный базис,
отвечающий оптимальной производственной программе:
Помимо этого в третьей симплексной таблице получен обращенный базис,
отвечающий оптимальной производственной программе:
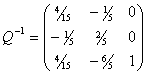 тогда можно проверить выполнение соотношения
тогда можно проверить выполнение соотношения 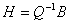 : :
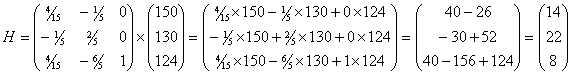 а т.к. из третьей симплексной таблицы:
а т.к. из третьей симплексной таблицы:
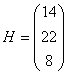 , следовательно, соотношение , следовательно, соотношение 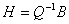 выполняется. выполняется.
2. Двойственная задача
Задача, двойственная линейной производственной задаче, например, может
заключаться в оценке выгоды от продажи сырья, используемого в производстве,
на сторону.
Например, в предыдущем п.1. рассмотрена линейная производственная задача по
выпуску четырех видов продукции с использованием трех видов ресурсов по
заданным технологиям. Предположим, некий предприниматель, занимающийся
производством других видов продукции с использованием трех таких же видов
ресурсов, предлагает «уступить» ему все имеющиеся ресурсы и обещает платить y
1 денежных единиц за каждую единицу первого ресурса, y2
денежных единиц за каждую единицу второго ресурса и y3 денежных
единиц за каждую единицу третьего ресурса. Возникает вопрос: при каких
значениях y1, y2, y3 можно согласиться с
предложением этого предпринимателя.
Т.к. в предыдущей задаче технологическая матрица 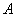 затрат любого ресурса на единицу каждой продукции, вектор
затрат любого ресурса на единицу каждой продукции, вектор 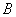 объемов ресурсов и вектор
объемов ресурсов и вектор 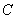 удельной прибыли имели вид:
удельной прибыли имели вид:
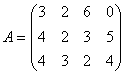 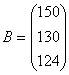 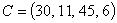 значит, для производства, например, первого вида продукции, предприятие должно
затратить 3 единицы ресурса первого вида, 4 единицы ресурса второго вида и 4
единицы ресурса третьего вида, за что оно получит прибыль 30 денежных единиц.
Следовательно, согласиться с предложением предпринимателя можно, если он
заплатит не меньше, т.е. в ценах y1, y2, y3
это условие будет иметь вид:
значит, для производства, например, первого вида продукции, предприятие должно
затратить 3 единицы ресурса первого вида, 4 единицы ресурса второго вида и 4
единицы ресурса третьего вида, за что оно получит прибыль 30 денежных единиц.
Следовательно, согласиться с предложением предпринимателя можно, если он
заплатит не меньше, т.е. в ценах y1, y2, y3
это условие будет иметь вид:
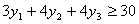 Аналогично и с продукцией второго, третьего и четвертого вида, при этом, за
все имеющиеся ресурсы, предприниматель должен заплатить не меньше:
Аналогично и с продукцией второго, третьего и четвертого вида, при этом, за
все имеющиеся ресурсы, предприниматель должен заплатить не меньше:
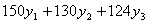 денежных единиц.
Следовательно, предприниматель будет искать такие значения y1, y
2, y3, при которых эта сумма была бы как можно меньше. При этом
речь идет о ценах, которые зависят не от цен по которым эти ресурсы были
когда-то приобретены, а о ценах зависящих от применяемых в производстве
технологий, объемов ресурсов и прибыли, которую возможно получить за
произведенную продукцию.
Таким образом, задача определения расчетных оценок ресурсов приводит к задаче
линейного программирования: найти вектор двойственных оценок денежных единиц.
Следовательно, предприниматель будет искать такие значения y1, y
2, y3, при которых эта сумма была бы как можно меньше. При этом
речь идет о ценах, которые зависят не от цен по которым эти ресурсы были
когда-то приобретены, а о ценах зависящих от применяемых в производстве
технологий, объемов ресурсов и прибыли, которую возможно получить за
произведенную продукцию.
Таким образом, задача определения расчетных оценок ресурсов приводит к задаче
линейного программирования: найти вектор двойственных оценок
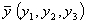 минимизирующий общую оценку всех ресурсов
минимизирующий общую оценку всех ресурсов
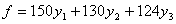 при условии, что по каждому виду продукции суммарная оценка всех ресурсов,
затрачиваемых на производство единицы продукции, не меньше прибыли,
получаемой от реализации единицы этой продукции, т.е.:
при условии, что по каждому виду продукции суммарная оценка всех ресурсов,
затрачиваемых на производство единицы продукции, не меньше прибыли,
получаемой от реализации единицы этой продукции, т.е.:
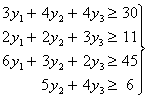 причем оценки ресурсов не могут быть отрицательными, т.е.:
причем оценки ресурсов не могут быть отрицательными, т.е.: 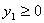 , , 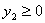 , , 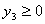 Решение полученной задачи можно найти с помощью второй теоремы
двойственности: дефицитный (избыточный) ресурс, полностью (неполностью)
используемый по оптимальному плану производства, имеет положительную
(нулевую) оценку, и технология, применяемая с ненулевой (нулевой)
интенсивностью, имеет нулевую (положительную) оценку.
Т.е. для оптимальных решений
Решение полученной задачи можно найти с помощью второй теоремы
двойственности: дефицитный (избыточный) ресурс, полностью (неполностью)
используемый по оптимальному плану производства, имеет положительную
(нулевую) оценку, и технология, применяемая с ненулевой (нулевой)
интенсивностью, имеет нулевую (положительную) оценку.
Т.е. для оптимальных решений 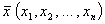 и
и 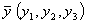 пары двойственных
задач необходимо и достаточно выполнение условий: пары двойственных
задач необходимо и достаточно выполнение условий:
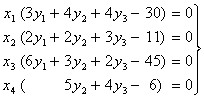 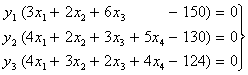 Ранее в п.1. было найдено, что
Ранее в п.1. было найдено, что 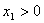 , , 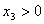 , а , а 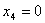 и и 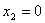 , тогда: , тогда:
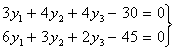 Но т.к. третий ресурс был избыточным (см. п.1.), то по второй теореме
двойственности, его двойственная оценка равна нулю, т.е.
Но т.к. третий ресурс был избыточным (см. п.1.), то по второй теореме
двойственности, его двойственная оценка равна нулю, т.е. 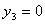 . Тогда переходим к новой системе уравнений:
. Тогда переходим к новой системе уравнений:
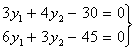 от куда получаем:
от куда получаем: 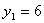 , , 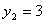 Таким образом, получили двойственные оценки ресурсов:
Таким образом, получили двойственные оценки ресурсов:
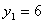 , , 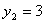 , , 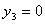 тогда общая оценка всех ресурсов равна:
тогда общая оценка всех ресурсов равна:
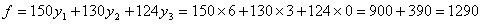 То же самое решение значений двойственных оценок содержится в последней
строке симплексной таблицы 1 и имеет определенный экономический смысл:
То же самое решение значений двойственных оценок содержится в последней
строке симплексной таблицы 1 и имеет определенный экономический смысл:
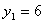
| Показывает, что добавление одной единицы первого ресурса обеспечит прирост прибыли в 6 денежных единиц. | 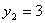
| Показывает, что добавление одной единицы второго ресурса обеспечит прирост прибыли в 3 денежные единицы. |
Одновременно технологические оценки из той же строки симплексной таблицы:
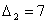
| Показывает, что если произвести одну единицу продукции второго вида (не входящую в оптимальную производственную программу), то это уменьшит прибыль на 7 денежных единиц | 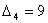
| Показывает, что если увеличить выпуск продукции четвертого вида на одну единицу, то это уменьшит прибыль на 9 денежных единиц |
3. Задача о «Расшивке узких мест производства»
Задача о «расшивке узких мест производства» заключается в том, что, например,
когда в процессе производства происходит изменение объема какого-либо
ресурса, используемого в производстве, то, соответственно изменяется план
производства и прибыль предприятия, получаемая от реализации готовой
продукции. Это может происходить по различным причинам, например: сломался
станок, поставщик предлагает сырье в большем количестве и т.п.
Поэтому, когда какой-либо ресурс используется полностью, то уменьшение объема
этого ресурса, может повлиять на всю структуру плана производства и прибыль
предприятия. Следовательно, такой ресурс, образующий «узкие места
производства», желательно иметь с некоторым запасом, т.е. заказывать
дополнительно, чтобы сохранить структуру плана производства и получить
возможность увеличить прибыль предприятия.
Для примера возьмем данные и результаты вычислений из п.1. и п.2., где
определено, что первый и второй ресурс используются полностью, и,
соответственно, именно их нужно заказывать дополнительно. Но в таких объемах,
чтобы сохранить структуру ранее найденной программы производства, и с
условием, что от поставщика можно получить дополнительно не более одной трети
первоначально выделенного объема ресурса любого вида. Следовательно, задача
сводиться к нахождению объемов приобретения дополнительных ресурсов,
удовлетворяющих указанным условиям, и вычислению дополнительной возможной
прибыли.
Тогда, пусть 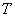 – вектор дополнительных объемов ресурсов: – вектор дополнительных объемов ресурсов:
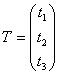 при этом, для сохранения структуры производственной программы, должно
выполняться условие устойчивости двойственных оценок:
при этом, для сохранения структуры производственной программы, должно
выполняться условие устойчивости двойственных оценок:
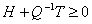 Т.к.
Т.к. 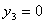 , то задача состоит в том, чтобы найти вектор: , то задача состоит в том, чтобы найти вектор:
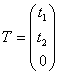 максимизирующий суммарный прирост прибыли:
максимизирующий суммарный прирост прибыли:
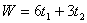
| (3.1) |
Страницы: 1, 2, 3, 4
|
|
|
|
|

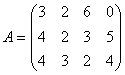
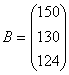
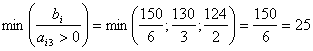 Оно соответствует первому уравнению в системе (1.3), и показывает какое
количество изделий третьего вида предприятие может изготовить с учетом объемов
сырья первого вида. Следовательно, в базис вводим неизвестную x3, а
исключаем от туда неизвестную x5. Тогда принимаем первое уравнение в
системе (1.3) за разрешающее, а разрешающим элементом будет a13=6.
Применив формулы исключения, переходим к новому предпочитаемому виду системы
с соответствующим базисным допустимым решением.
Полный процесс решения приведен в таблице 1, где в последней строке третьей
таблицы нет ни одного отрицательного относительного оценочного коэффициента
Оно соответствует первому уравнению в системе (1.3), и показывает какое
количество изделий третьего вида предприятие может изготовить с учетом объемов
сырья первого вида. Следовательно, в базис вводим неизвестную x3, а
исключаем от туда неизвестную x5. Тогда принимаем первое уравнение в
системе (1.3) за разрешающее, а разрешающим элементом будет a13=6.
Применив формулы исключения, переходим к новому предпочитаемому виду системы
с соответствующим базисным допустимым решением.
Полный процесс решения приведен в таблице 1, где в последней строке третьей
таблицы нет ни одного отрицательного относительного оценочного коэффициента
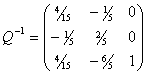 тогда можно проверить выполнение соотношения
тогда можно проверить выполнение соотношения 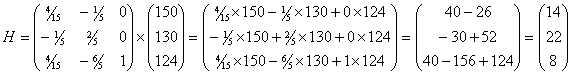 а т.к. из третьей симплексной таблицы:
а т.к. из третьей симплексной таблицы:
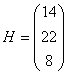 , следовательно, соотношение
, следовательно, соотношение 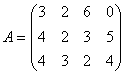
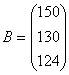
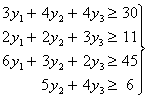 причем оценки ресурсов не могут быть отрицательными, т.е.:
причем оценки ресурсов не могут быть отрицательными, т.е.: 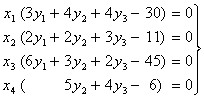
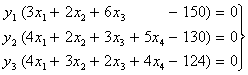 Ранее в п.1. было найдено, что
Ранее в п.1. было найдено, что 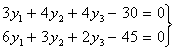 Но т.к. третий ресурс был избыточным (см. п.1.), то по второй теореме
двойственности, его двойственная оценка равна нулю, т.е.
Но т.к. третий ресурс был избыточным (см. п.1.), то по второй теореме
двойственности, его двойственная оценка равна нулю, т.е. 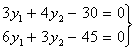 от куда получаем:
от куда получаем: 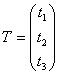 при этом, для сохранения структуры производственной программы, должно
выполняться условие устойчивости двойственных оценок:
при этом, для сохранения структуры производственной программы, должно
выполняться условие устойчивости двойственных оценок:
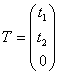 максимизирующий суммарный прирост прибыли:
максимизирующий суммарный прирост прибыли:

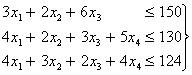
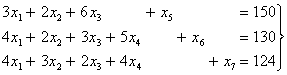
 45
45